تبدیل موجک — از صفر تا صد

تبدیل موجک (Wavelet Transform) یکی از تبدیلات مهم ریاضی است که در حوزه‌های مختلف علوم کاربرد دارد. ایده اصلی تبدیل موجک این است که بر ضعف‌ها و محدودیت‌های موجود در تبدیل فوریه غلبه کند. این تبدیل را بر خلاف تبدیل فوریه، می‌توان در مورد سیگنال‌های غیر ایستا و سیستم‌های دینامیک نیز مورد استفاده قرار داد. در این مطلب قصد داریم تا به بررسی تبدیل موجک و کاربرد آن در پردازش سیگنال و یادگیری ماشین بپردازیم. ابتدا مفاهیم، تئوری و عملکرد تبدیل موجک پیوسته و گسسته و تمایز آن با تبدیل فوریه را بیان می‌کنیم و سپس مثال‌هایی کاربردی از اعمال تبدیل موجک روی دو دیتاست UCI-HAR و ECG و دسته‌بندی داده‌های آن‌ها با استفاده از الگوریتم‌های یادگیری ماشین و یادگیری عمیق در محیط پایتون را مورد بررسی قرار می‌دهیم. در نهایت، کدهای پیاده‌سازی تبدیل موجک در محیط متلب بدون استفاده از توابع آماده را بیان می‌کنیم و آن را روی دیتاست ال نینو پیاده‌سازی می‌کنیم.

تبدیلات ریاضی کاربردهای فراوانی در پردازش و طبقه‌بندی داده‌های مختلف مانند سیگنال‌ها و سری‌های زمانی (Time Series) دارند. به عنوان مثال، با استفاده از تبدیل فوریه (Fourier Transform) که در مطالب قبلی مجله فرادرس مورد بررسی قرار گرفته است، می‌توان یک سیگنال را از حوزه زمان به حوزه فرکانس منتقل کرد. پیک‌های ظاهر شده در نمودار طیف فرکانسی یک سیگنال پس از اعمال تبدیل فوریه، نشان دهنده فرکانس‌هایی است که در آن سیگنال غالب هستند. هر چقدر این پیک‌ها بزرگتر و تیزتر باشند، آن فرکانس در سیگنال حضور بیشتر و موثرتری دارد. محل قرار گرفتن پیک (مقدار فرکانس) و ارتفاع آن (دامنه فرکانس) در یک نمودار طیف فرکانسی، می‌توانند به عنوان ورودی برای الگوریتم‌هایی طبقه‌بندی مانند جنگل تصادفی (Random Forest) و یا ارتقای گرادیان (Gradient Boosting) مورد استفاده قرار گیرند.

این تکنیک ساده برای بسیاری از مسائل عملکرد فوق‌العاده و دقت بسیار بالایی به همراه خواهد داشت. اما قاعده کلی که در مورد تبدیل فوریه وجود دارد این است که تبدیل فوریه تا زمانی که طیف فرکانسی یک سیگنال از لحاظ آماری ایستا (Stationary) باشد، به خوبی عمل خواهد کرد. ایستا بودن طیف فرکانسی به این معنی است که فرکانس‌های ظاهر شده در یک سیگنال، وابسته به زمان نباشند. به عبارت دیگر، اگر یک سیگنال شامل فرکانس X هرتز باشد، این فرکانس باید به صورت برابر در تمام طول سیگنال وجود داشته باشد.

هرچه یک سیگنال بیشتر غیر ایستا یا دینامیک باشد، نتیجه بدتر خواهد بود. پردازش سیگنال‌های غیر ایستا معمولا از دشواری بیشتری برخوردار است و برای آنالیز آن‌ها باید از تکنیک‌ها و پیش پردازش‌های دیگری استفاده کنیم. بسیاری از سیگنال‌های واقعی موجود در طبیعت دارای طبیعت غیر ایستا هستند. هنگامی که تلاش داریم سیگنال‌های ECG، بازار بورس، داده‌های تجهیزات و سنسورها و... را در پروژه‌های عملی مورد پردازش قرار دهیم، به احتمال زیاد با سیگنال‌های غیر ایستا و سیستم‌های دینامیک رو به رو خواهیم شد. یک راه حل بسیار عالی برای پردازش سیگنال‌های غیر ایستا، استفاده از تبدیل موجک به جای تبدیل فوریه است.

با این که تبدیل موجک یک ابزار بسیار قدرتمند برای پردازش و طبقه‌بندی سیگنال‌ها و سری‌های زمانی دینامیک محسوب می‌شود، اما هنوز در علم داده به صوررت گسترده مورد استفاده قرار نمی‌گیرد و از محبوبیت بالایی برخوردار نیست. احتمالا دلیل این امر، نیاز به داشتن دانش اولیه درباره ریاضیات، تبدیل فوریه و پردازش سیگنال است، تا پس از آن، ریاضیات نهفته در تبدیل موجک به صورت کامل قابل درک باشد. البته بسیاری از مراجع و کتاب‌ها به صورت تئوری تبدیل موجک را مورد بررسی قرار داده‌اند، در حالی که دانش عملی کافی درباره نحوه استفاده از آن به ندرت مورد بحث قرار گرفته است.

به همین دلیل، در این مطلب می‌خواهیم به بیان مباحث تئوری مرتبط با تبدیل موجک بپردازیم و با کاربردهای عملی تبدیل موجک آشنا شویم، اما به صورت عمیق ریاضیات آن را مورد بررسی قرار نمی‌دهیم. در هر گام از مطلب، کدهای پایتون را ارائه می‌دهیم، به صورتی که در پایان قادر باشید از تبدیل موجک در پروژه‌های خود استفاده کنید. در کدهایی که در ادامه نوشته می‌شود، از پکیج PyWavelets استفاده شده است، بنابراین توصیه می‌شود تا این پکیج را ابتدا با دستور «pip install pywavelets» نصب نمایید.

از تبدیل فوریه به تبدیل موجک

همان طور که می‌دانیم، تبدیل فوریه از طریق ضرب کردن سیگنال مورد پردازش در قطاری از سیگنال‌های سینوسی با فرکانس‌های مختلف عمل می‌کند. در واقع، از این راه می‌توانیم تعیین کنیم که کدام فرکانس‌ها در سیگنال مورد پردازش وجود دارند. اگر عملگر ضرب نقطه‌ای بین سیگنال مورد نظر و یک سیگنال سینوسی با فرکانس مشخص، برابر با یک عدد با دامنه بزرگ شود، آن‌گاه می‌توان نتیجه گرفت که هم‌پوشانی زیادی بین این دو سیگنال وجود دارد و در نتیجه آن فرکانس مشخص در طیف فرکانسی سیگنال مورد نظر نیز مشاهده خواهد شد. قطعا دلیل این امر از آنجایی ناشی می‌شود که عملگر ضرب نقطه‌ای معیاری برای اندازه‌گیری میزان هم‌پوشانی و شباهت بین دو بردار یا دو سیگنال است.

فیلم آموزش شبکه های مخابراتی (رایگان) در فرادرس

کلیک کنید

نکته‌ای که در مورد تبدیل فوریه می‌توان به آن اشاره کرد این است که در حوزه فرکانس دارای رزولوشن بالایی است، در حالی‌ که در حوزه زمان از رزولوشن صفر برخوردار است. به عبارت دیگر، تبدیل فوریه این توانایی را دارد که به ما بگوید دقیقا چه فرکانس‌هایی در یک سیگنال وجود دارند، اما نمی‌توان با استفاده از آن تعیین کرد که فرکانس مورد نظر در چه لحظه‌ای از زمان در سیگنال اتفاق می‌افتد. این مفهوم را می‌توان به سادگی با استفاده از قطعه کد زیر به نمایش در آورد:

1t_n = 1
2N = 100000
3T = t_n / N
4f_s = 1/T
5 
6xa = np.linspace(0, t_n, num=N)
7xb = np.linspace(0, t_n/4, num=N/4)
8 
9frequencies = [4, 30, 60, 90]
10y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb)
11y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb)
12y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb)
13y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb)
14 
15composite_signal1 = y1a + y2a + y3a + y4a
16composite_signal2 = np.concatenate([y1b, y2b, y3b, y4b])
17 
18f_values1, fft_values1 = get_fft_values(composite_signal1, T, N, f_s)
19f_values2, fft_values2 = get_fft_values(composite_signal2, T, N, f_s)
20 
21fig, axarr = plt.subplots(nrows=2, ncols=2, figsize=(12,8))
22axarr[0,0].plot(xa, composite_signal1)
23axarr[1,0].plot(xa, composite_signal2)
24axarr[0,1].plot(f_values1, fft_values1)
25axarr[1,1].plot(f_values2, fft_values2)
26(...)
27plt.tight_layout()
28plt.show()

خروجی این قطعه کد در تصویر زیر دیده می‌شود. در این تصویر سیگنال‌های اصلی به همراه طیف فرکانسی هر کدام نشان داده شده است.

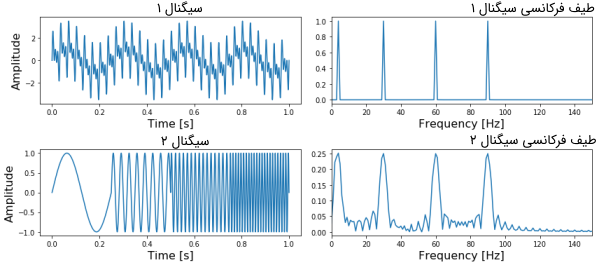
در تصاویر بالا، در ردیف اول سیگنال اصلی به همراه طیف فرکانسی آن دیده می‌شود که شامل چهار فرکانس در تمام زمان‌ها است و در ردیف پایین می‌توان دید که سیگنال دوم نیز چهار فرکانس مختلف اما در چهار زمان متفاوت دارد.

در این تصویر، اولین سیگنال از سمت چپ، بر اساس تصویر طیف فرکانسی خود، چهار فرکانس مختلف در ۶۰، ۳۰، ۴ و ۹۰ هرتز دارد. این فرکانس‌ها در تمام زمان‌ها وجود دارند. در سیگنال دوم نیز چهار فرکانس مشابه وجود دارد، اما تفاوتی که دارد این است که فرکانس اول فقط در ربع اول از سیگنال، فرکانس دوم در ربع دوم سیگنال، فرکانس سوم در ربع سوم و فرکانس چهام فقط در ربع آخر سیگنال وجود دارند.

نکته‌ مهمی که در اینجا باید به آن توجه شود این است که هر دو نمودار طیف فرکانسی در تصویر بالا، دارای چهار پیک دقیقا یکسان در ۴ فرکانس ذکر شده هستند. بنابراین با استفاده از تبدیل فوریه نمی‌توان به این واقعیت پی برد که فرکانس در سیگنال اصلی دقیقا در کجا اتفاق می‌افتد. دقیقا به همین دلیل است که در مثال بالا نیز تبدیل فوریه نتوانست به ما در تمایز و تشخیص دو سیگنال از یکدیگر کمک کند. توجه کنید که وقوع لبه‌های گذرا جانبی در طیف فرکانسی سیگنال دوم، به دلیل ناپیوستگی بین چهار فرکانس در سیگنال است.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

برای غلبه بر این مشکل، روش تبدیل فوریه زمان کوتاه (Short-Time Fourier Transform) یا STFT مورد استفاده قرار می‌گیرد. در این روش، سیگنال اصلی به چندین بخش با طول یکسان تقسیم می‌شوند. این بخش‌ها ممکن است با یکدیگر هم‌پوشانی داشته باشند و یا فاقد هم‌پوشانی باشند. با استفاده از پنجره‌های لغزشی (Sliding Window)، سیگنال را قبل از اعمال تبدیل فوریه به چندین بخش تقسیم می‌کنیم. ایده اصلی در این روش بسیار ساده است. اگر سیگنال را مثلا به 10 قسمت تقسیم کرده باشیم و تبدیل فوریه در بخش دوم فرکانس خاصی را تشخیص دهد، بنابراین با قطعیت بالا می‌توان گفت که این فرکانس در بازه بین $$\frac {2} {10}$$ و $$\frac {3} {10}$$ از سیگنال اصلی به وقوع می‌پیوندد.

اما عیب اصلی که در این روش وجود دارد این است که با یک محدودیت فیزیکی در تبدیل فوریه رو به رو خواهد شد که عدم قطعیت نام دارد. در این روش، هرچه اندازه پنجره‌ها را کوچک‌تر کنیم، قادر خواهیم بود به صورت دقیق‌تر تعیین کنیم که یک فرکانس در چه زمانی از سیگنال اصلی به وقوع پیوسته است، اما از طرف دیگر اطلاعات کم‌تری را راجع به مقدار فرکانس سیگنال اصلی به دست خواهیم آورد. به صورت مشابه، هر چه اندازه پنجره‌ها را بزرگ‌تر انتخاب کنیم، اطلاعات بیشتری راجع به مقدار فرکانس و اطلاعات کمتری راجع به زمان وقوع فرکانس به دست خواهیم آورد.

روش بهتری که برای آنالیز یک سیگنال با طیف فرکانسی دینامیک وجود دارد، استفاده از تبدیل موجک است. تبدیل موجک هم در حوزه زمان و هم در حوزه فرکانس دارای رزولوشن بالایی است. این تبدیل نه تنها مقدار فرکانس‌های موجود در سیگنال را مشخص می‌کند، بلکه تعیین می‌کند که آن فرکانس‌ها در چه زمانی از سیگنال به وقوع می‌پیوندند. تبدیل موجک این توانایی را از طریق کار کردن در مقیاس‌های (Scale) مختلف به دست می‌آورد. در تبدیل موجک، ابتدا سیگنال را با مقیاس یا پنجره بزرگ در نظر می‌گیریم و ویژگی‌های بزرگ (Large Features) آن را آنالیز می‌کنیم. در گام بعد، با پنجره‌‌های کوچک به سیگنال نگاه می‌کنیم و ویژگی‌های کوچک سیگنال را به دست می‌آوریم. در تصویر زیر رزولوشن حوزه زمان و فرکانس در روش تبدیل‌های مختلف به نمایش درآمده است.

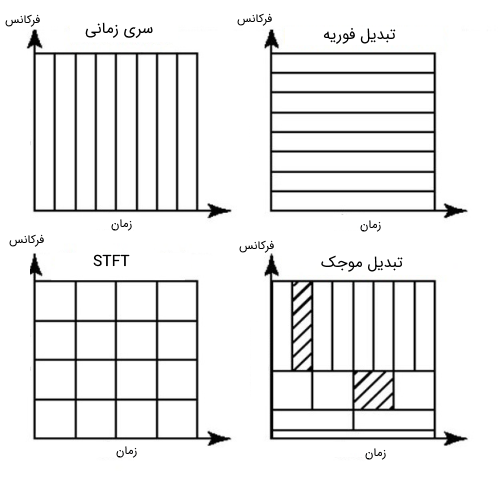
در تصویر بالا، اندازه و جهت بلوک‌ها نشان‌دهنده مقدار رزولوشن در آن تبدیل است، به عبارت دیگر بلوک‌ها در هر تبدیل تعیین می‌کنند که در حوزه زمان و فرکانس می‌توان ویژگی‌های تا چه مقدار کوچک را با استفاده از آن تبدیل تشخیص داد. سیگنال اصلی که در حوزه زمان است، دارای رزولوشن بالا در حوزه زمان و رزولوشن صفر در حوزه فرکانس است. این ویژگی به این معنی است که می‌توانیم ویژگی‌های بسیار کوچکی را در حوزه زمان تشخیص دهیم، اما در حوزه فرکانس هیچ ویژگی قابل تمایز نیست.

اما تبدیل فوریه زمان کوتاه، دارای رزولوشن با اندازه متوسط در هر دو حوزه زمان و فرکانس است. رزولوشن تبدیل موجک به صورت زیر تغییر می‌کند:

• برای مقادیر فرکانس‌های کوچک، رزولوشن بالا در حوزه فرکانس و رزولوشن پایین در حوزه زمان دارد.
• برای مقادیر فرکانس‌های بالا، رزولوشن پایین در حوزه فرکانس و رزولوشن بالا در حوزه زمان دارد.

بنابراین در حالت کلی می‌توان گفت تبدیل موجک به صورت مصالحه‌ای عمل می‌کند. در مقیاس‌هایی که مشخصه‌های وابسته به زمان جذاب‌تر هستند، تبدیل موجک دارای رزولوشن بالاتر در حوزه زمان و در مقیاس‌هایی که مشخصه‌های وابسته به فرکانس جذاب‌تر هستند، دارای رزولوشن بالاتر در حوزه فرکانس است. این نوع مصالحه دقیقا همان هدفی است که در پردازش سیگنال مورد نظر است.

نحوه عملکرد تبدیل موجک

همان طور که اشاره کردیم، تبدیل فوریه برای آنالیز سیگنال از یک سری امواج سینوسی با فرکانس‌های مختلف استفاده می‌کند. در این حالت، سیگنال به صورت ترکیبی خطی از سیگنال‌های سینوسی نمایش داده می‌شود. اما تبدیل موجک از تعدادی توابع به نام موجک استفاده می‌کند که هر کدام مقیاس متفاوتی دارند. همان طور که می‌دانیم معنی واژه موجک، موج کوچک است و توابع موجک نیز دقیقا به همین صورت کوچک هستند.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

در تصویر زیر تفاوت بین یک سیگنال سینوسی و یک موجک نشان داده شده است.

با دقت در تصویر بالا، کاملا مشخص است که سیگنال سینوسی در یک لحظه خاص از زمان واقع نشده است. این سیگنال از بی‌نهایت شروع می‌شود و تا بی‌نهایت ادامه می‌یابد، در حالی که یک موجک در لحظه خاصی از زمان واقع شده است. این ویژگی به تبدیل موجک اجازه می‌دهد تا علاوه بر اطلاعات فرکانسی، اطلاعات زمانی را نیز به دست آورد.

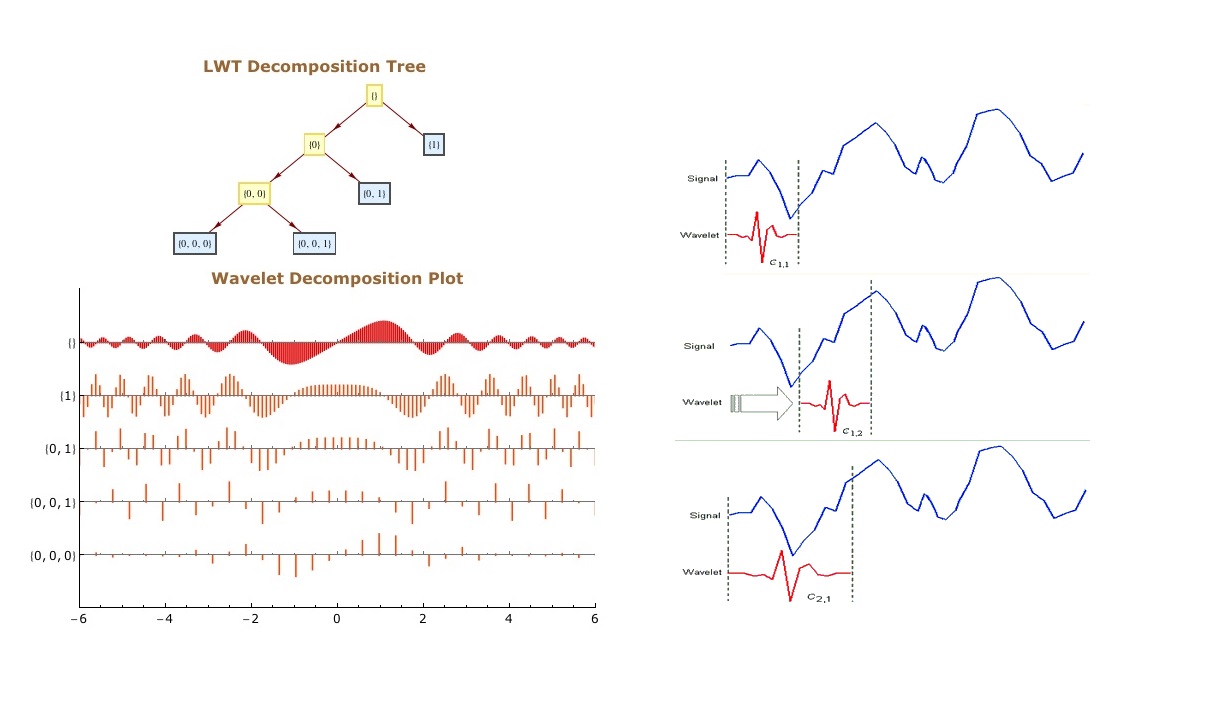
چون موجک در زمان واقع شده است، در نتیجه می‌توان سیگنال اصلی را در لحظات مختلف از زمان در موجک ضرب کرد. در گام نخست، با نقاط ابتدایی سیگنال شروع می‌کنیم و به تدریج موجک را به سمت انتهای سیگنال حرکت می‌دهیم. این عمل را کانولوشن (Convolution) می‌گویند. بعد از این که کانولوشن را با سیگنال موجک اصلی (موجک مادر) انجام دادیم، می‌توانیم آن را به نحوی مقیاس‌دهی کنیم که بزرگ‌تر شود و دوباره فرایند را تکرار کنیم. این فرایند در تصویر متحرک زیر نشان داده شده است.

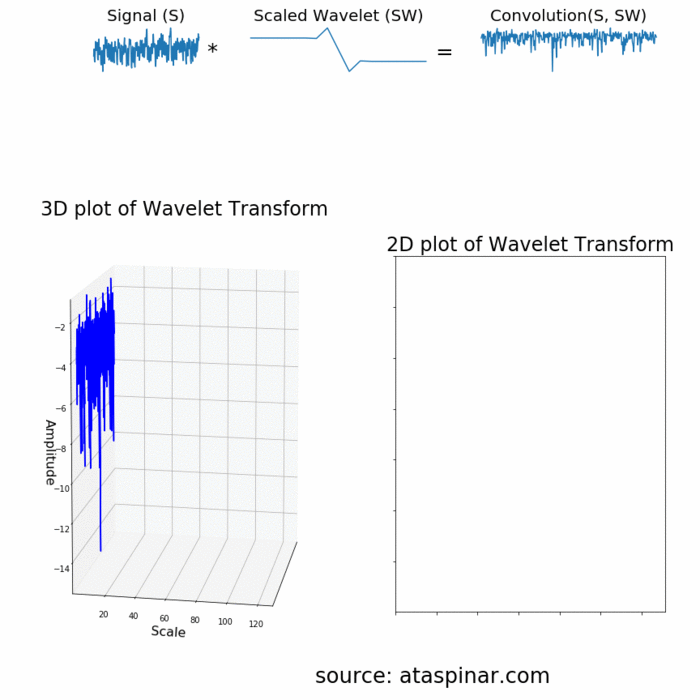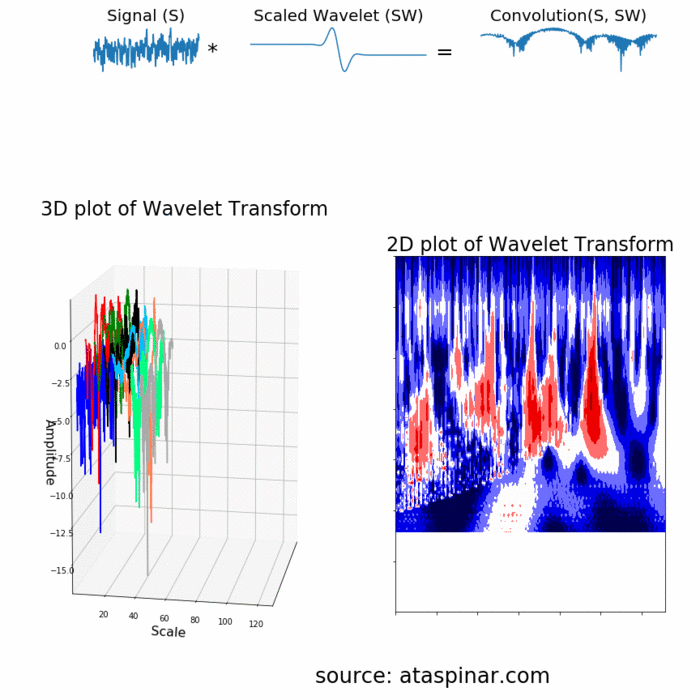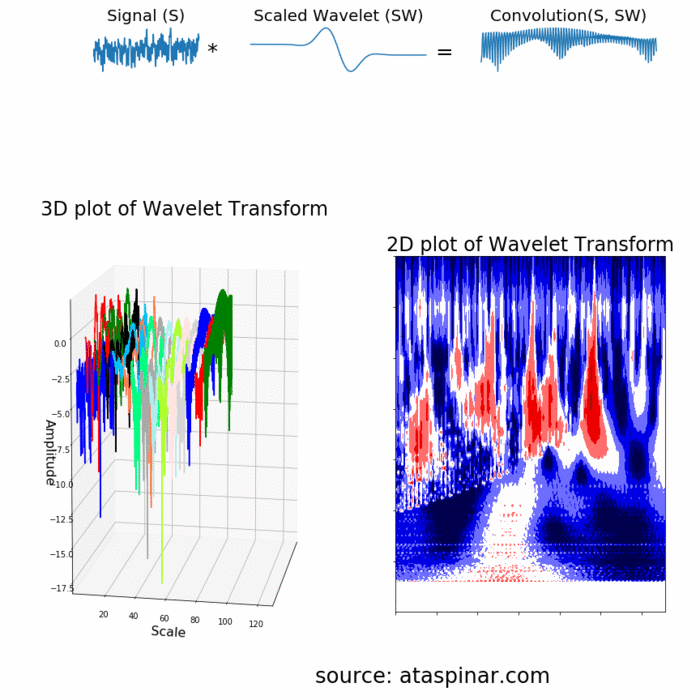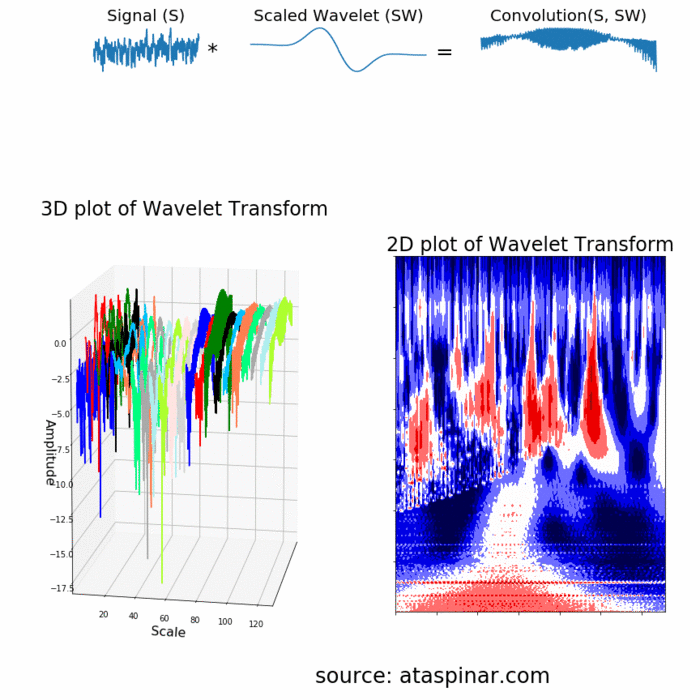
همان طور که از تصویر بالا مشخص است، تبدیل موجک یک سیگنال تک بعدی، دارای دو بعد است. این خروجی دو بعدی مربوط به تبدیل موجک، نمایش سیگنال اصلی بر حسب مقیاس و زمان است که به طیف اسپکتروگرام (Spectrogram) یا اسکالوگرام (Scaleogram) معروف است. در تصویر بالا، ابتدا تبدیل موجک به صورت سه بعدی و سپس به صورت دو بعدی نیز ترسیم شده است. ممکن است این سوال پیش بیاید که بُعد مقیاس (Scale) در تصویر اسپکتروگرام نشان‌دهنده چیست؟ در واقع، چون کلمه فرکانس اغلب برای تبدیل فوریه مورد استفاده قرار می‌گیرد، تبدیل موجک اغلب با مقیاس بیان می‌شود. در نتیجه در تبدیل موجک، دو بُعد اسپکتروگرام، زمان و مقیاس هستند. در مسائلی که فرکانس مناسبت‌تر وشهودی‌تر از مقیاس باشد، می‌توان از طریق فرمول زیر، مقیاس را به شبه‌فرکانس (Pseudo-Frequencies) تبدیل کرد:

$$f_a = \frac {f_c} {a}$$

در این فرمول، $$f_a$$ برابر با شبه‌فرکانس، $$f_c$$ فرکانس مرکزی سیگنال موجک مادر و $$a$$ فاکتور مقیاس (Scaling Factor) است. واضح است که فاکتور مقیاس بالاتر (موجک طولانی‌تر) متناظر با فرکانس‌های پایین‌تر است، بنابراین با مقیاس‌دهی به سیگنال موجک در حوزه زمان، می‌توانیم فرکانس‌های کوچک‌تر را آنالیز کنیم و در نتیجه به رزولوشن بالاتر در حوزه فرکانس می‌رسیم. به طریق مشابه، با استفاده از مقیاس کوچک‌تر، رزولوشن در حوزه زمان بالاتر خواهد رفت. بنابراین می‌توان گفت مقیاس، معکوس فرکانس در تبدیل فوریه است. پکیج PyWavelets در پایتون، شامل تابع  scale2frequency است تا تبدیل را از حوزه مقیاس به حوزه فرکانس انجام دهد.

انواع مختلف تبدیل موجک

تفاوت دیگری که بین تبدیل فوریه و تبدیل موجک وجود دارد، این است که تبدیل موجک انواع مختلفی دارد. برای انواع مختلف تبدیل موجک، مصالحه بین فشردگی (Compact) و صاف بودن (Smooth) با یکدیگر تفاوت دارند. این ویژگی بدین معنی است که می‌توانیم نوع خاصی از تبدیل موجک را انتخاب کنیم که با ویژگی (Features) مورد نظر برای استخراج از سیگنال تناسب بیشتری داشته باشد.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

به عنوان مثال کتابخانه PyWavelets شامل ۱۴ موجک مادر (انواع موجک) است. در قطعه کد زیر انواع این خانواده موجک‌ها را می‌توان مشاهده کرد.

1import pywt
2print(pywt.families(short=False))
3['Haar', 'Daubechies', 'Symlets', 'Coiflets', 'Biorthogonal', 'Reverse biorthogonal', 
4'Discrete Meyer (FIR Approximation)', 'Gaussian', 'Mexican hat wavelet', 'Morlet wavelet', 
5'Complex Gaussian wavelets', 'Shannon wavelets', 'Frequency B-Spline wavelets', 'Complex Morlet wavelets']

هر خانواده از موجک‌ها دارای شکل، فشردگی و همواری متفاوتی هستند و برای هدف متمایزی مورد استفاده قرار می‌گیرد. چون فقط دو شرط ریاضی وجود دارد که تابع موجک باید در آن صدق کند، در نتیجه تولید انواع مختلف موجک کار آسانی است. دو شرط ریاضی که موجک باید در آن‌ها صدق کند، قیود متعامدسازی (Orthogonalization) و نرمال‌سازی (Normalization) نام دارند. بر اساس این قیود، یک موجک باید اولا انرژی محدود (Finite Energy) داشته باشد و دوما میانگین آن برابر با صفر باشد.

انرژی محدود به این معنی است که سیگنال در زمان و فرکانس متمرکز (Localized) باشد، انتگرال‌پذیر باشد و ضرب داخلی بین سیگنال و موجک همیشه وجود داشته باشد. همچنین بر اساس شرط مقبولیت دوم، موجک باید دارای میانگین صفر در حوزه زمان باشد یا به عبارت دیگر، در حوزه زمان و در فرکانس صفر، مقدار آن برابر با صفر باشد. این شرط برای اطمینان از انتگرال‌پذیری و نیز محاسبه معکوس تبدیل موجک بسیار ضروری است. علاوه بر این داریم:

• یک موجک می‌تواند متعامد (Orthogonal) یا غیر متعامد باشد.
• یک موجک می‌تواند متعامد دو طرفه (Bi-Orthogonal) باشد یا نباشد.
• یک موجک می‌تواند متقارن (Symmetric) یا غیرمتقارن باشد.
• یک موجک می‌تواند حقیقی یا مختلط باشد. موجک همیشه به دو قسمت تقسیم می‌شود، قسمت حقیقی که نشان‌دهنده دامنه و قسمت موهومی که نشان‌دهنده فاز است.
• یک موجک نرمالیزه می‌شود تا دارای انرژی واحد باشد.

با استفاده از قطعه کد زیر می‌توانیم تصویری از خانواده‌های مختلف موجک را ترسیم کنیم. ردیف اول شامل چهار نوع موجک گسسته و ردیف دوم شامل چهار نوع موجک پیوسته است.

1discrete_wavelets = ['db5', 'sym5', 'coif5', 'bior2.4']
2continuous_wavelets = ['mexh', 'morl', 'cgau5', 'gaus5']
3
4list_list_wavelets = [discrete_wavelets, continuous_wavelets]
5list_funcs = [pywt.Wavelet, pywt.ContinuousWavelet]
6
7fig, axarr = plt.subplots(nrows=2, ncols=4, figsize=(16,8))
8for ii, list_wavelets in enumerate(list_list_wavelets):
9    func = list_funcs[ii]
10    row_no = ii
11    for col_no, waveletname in enumerate(list_wavelets):
12        wavelet = func(waveletname)
13        family_name = wavelet.family_name
14        biorthogonal = wavelet.biorthogonal
15        orthogonal = wavelet.orthogonal
16        symmetry = wavelet.symmetry
17        if ii == 0:
18            _ = wavelet.wavefun()
19            wavelet_function = _[0]
20            x_values = _[-1]
21        else:
22            wavelet_function, x_values = wavelet.wavefun()
23        if col_no == 0 and ii == 0:
24            axarr[row_no, col_no].set_ylabel("Discrete Wavelets", fontsize=16)
25        if col_no == 0 and ii == 1:
26            axarr[row_no, col_no].set_ylabel("Continuous Wavelets", fontsize=16)
27        axarr[row_no, col_no].set_title("{}".format(family_name), fontsize=16)
28        axarr[row_no, col_no].plot(x_values, wavelet_function)
29        axarr[row_no, col_no].set_yticks([])
30        axarr[row_no, col_no].set_yticklabels([])
31
32plt.tight_layout()
33plt.show()

خروجی این کد به صورت زیر است.

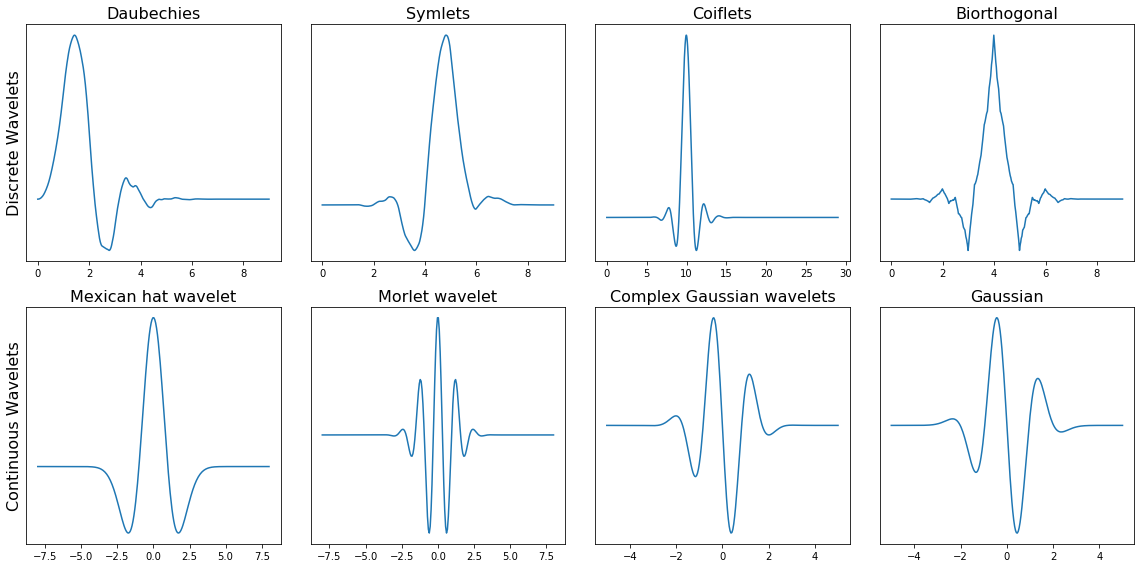
در هر یک از خانواده‌های موجک، زیرگروه‌های موجک مختلفی نیز وجود دارد که متعلق به آن خانواده است. برای تشخیص زیرگروه‌های مختلف در هر خانواده از موجک، باید به تعداد ضرایب (Vanishing Moments) و سطح تجزیه (Level of Decomposition) توجه کنیم. این مفهوم در کد زیر برای یک خانواده از موجک‌ها با نام Daubechies نشان داده شده است.

1import pywt
2import matplotlib.pyplot as plt
3
4db_wavelets = pywt.wavelist('db')[:5]
5print(db_wavelets)
6*** ['db1', 'db2', 'db3', 'db4', 'db5']
7
8fig, axarr = plt.subplots(ncols=5, nrows=5, figsize=(20,16))
9fig.suptitle('Daubechies family of wavelets', fontsize=16)
10for col_no, waveletname in enumerate(db_wavelets):
11    wavelet = pywt.Wavelet(waveletname)
12    no_moments = wavelet.vanishing_moments_psi
13    family_name = wavelet.family_name
14    for row_no, level in enumerate(range(1,6)):
15        wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level)
16        axarr[row_no, col_no].set_title("{} - level {}\n{} vanishing moments\n{} samples".format(
17            waveletname, level, no_moments, len(x_values)), loc='left')
18        axarr[row_no, col_no].plot(x_values, wavelet_function, 'bD--')
19        axarr[row_no, col_no].set_yticks([])
20        axarr[row_no, col_no].set_yticklabels([])
21plt.tight_layout()
22plt.subplots_adjust(top=0.9)
23plt.show()

خروجی این قطعه کد به صورت زیر است.

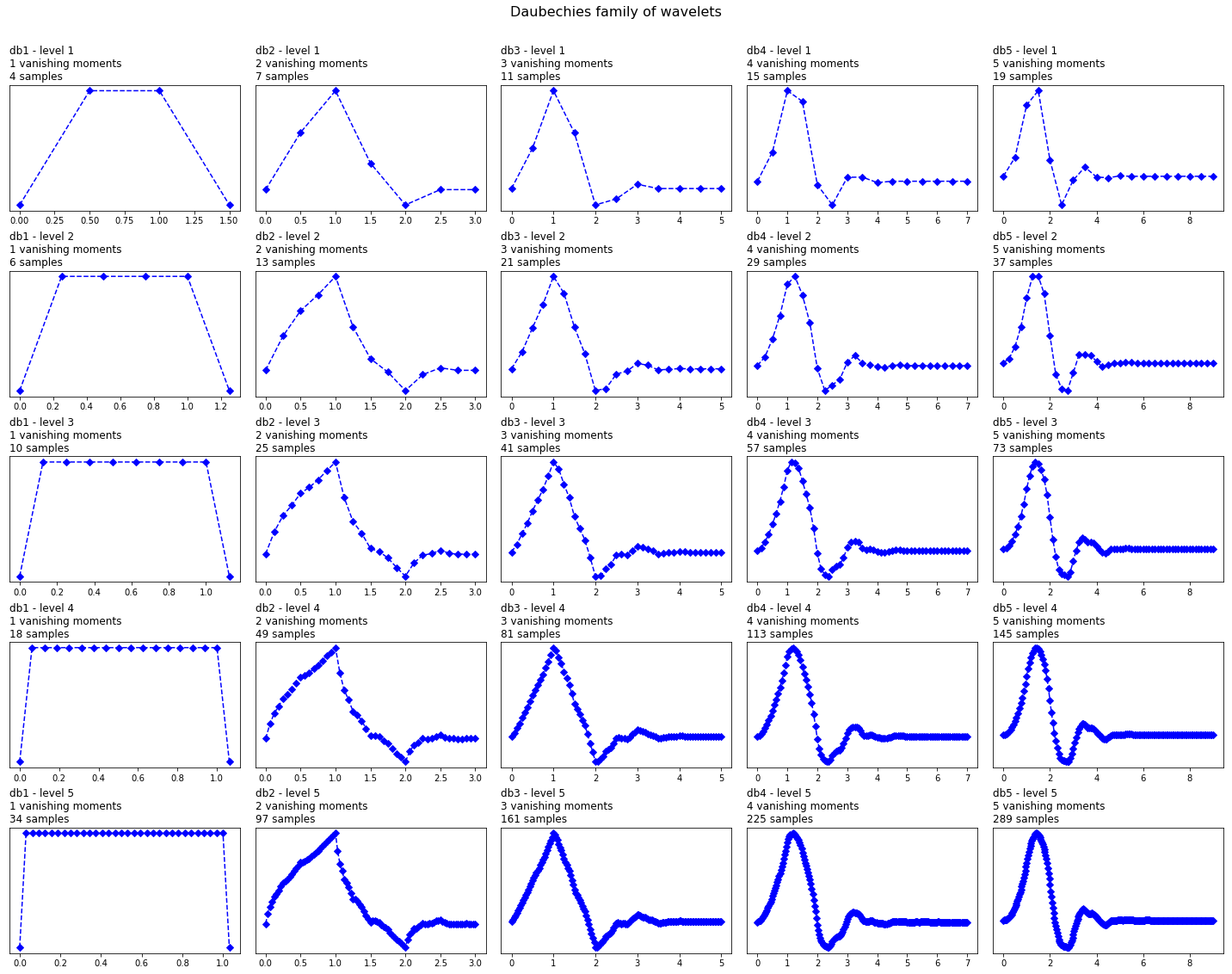
در تصویر بالا، می‌توانیم تبدیل موجک خانواده Daubechies یا به اختصار db را مشاهده کنیم. در ستون اول، تبدیل موجک db مرتبه (Order) اول (db1)، در ستون دوم تبدیل db2 و به همین ترتیب تا در ستون پنجم تبدیل موجک مرتبه ۵ ترسیم شده است.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

کتابخانه PyWavelets شامل موجک Daubechies تا مرتبه ۲۰ است. تعداد مرتبه‌های تبدیل موجک نشان‌دهنده تعداد لحظات محوشدگی (Vanishing Moments) است. بنابراین db3 دارای سه لحظه محوشدگی و db5 دارای ۵ لحظه محوشدگی است. تعداد لحظات محوشدگی به درجه تقریب و همواری (Smoothness) تبدیل موجک بستگی دارد. اگر یک تبدیل موجک دارای p لحظه محوشدگی باشد، آن‌گاه می‌تواند یک تابع چندجمله‌ای از درجه p-1 را تقریب بزند.

هنگام انتخاب کردن تبدیل موجک، می‌توانیم تعیین کنیم که درجه تجزیه (Level of Decomposition) باید چقدر باشد. به صورت پیش فرض کتابخانه PyWavelets بیشینه درجه تجزیه ممکن را برای سیگنال ورودی انتخاب می‌کند. بیشینه درجه تجزیه توسط دستور pywt.dwt_max_level مشخص می‌شود و به طول سیگنال ورودی و موجک بستگی دارد.

واضح است که هر چقدر تعداد لحظات محوشدگی افزایش یابد، درجه چندجمله‌ای موجک افزایش می‌یابد و هموارتر (نرم‌تر) می‌شود و هرچه درجه تجزیه افزایش یابد، تعداد نمونه‌هایی که موجک بر اساس آن بیان می‌شود، افزایش می‌یابد.

تبدیل موجک پیوسته و تبدیل موجک گسسته

همان طور که در تصاویر دیدیم، تبدیل موجک دارای دو نوع مختلف گسسته و پیوسته است.

فیلم آموزش شبکه های مخابراتی (رایگان) در فرادرس

کلیک کنید

از لحاظ ریاضی، یک تبدیل موجک پیوسته را می‌توان توسط تابع زیر توصیف کرد:

$$X_{\omega}(a,b) = \frac {1} {|a|^\frac{1} {2}} \int_{- \infty}^{\infty} x(t) \bar{\psi } (\frac {t-b} {a}) dt$$

در فرمول بالا، $$\psi (t)$$ موجک مادر پیوسته است که توسط فاکتور $$a$$ مقیاس و توسط فاکتور $$b$$ منتقل شده است. مقدار فاکتور مقیاس‌دهی و جابه‌جایی اعدادی پیوسته هستند، بنابراین تعداد بی شماری موجک وجود دارد. می‌توان موجک مادر را توسط فاکتور ۱٫۳ یا ۱٫۳۱۱۱۱ یا هر عدد دیگر مقیاس کرد.

اما زمانی که راجع به تبدیل موجک گسسته بحث می‌کنیم، تفاوت اصلی که وجود دارد این است که از مقادیر گسسته برای فاکتور مقیاس‌دهی و جابه‌جایی در این تبدیل استفاده می‌شود. فاکتور مقیاس به صورت اعداد توان دو افزایش می‌یابد، بنابراین $$a = 1,2,4, ...$$ خواهد بود. فاکتور جابه‌جایی به صورت اعداد صحیح افزایش می‌یابند، بنابراین $$b = 1,2,3,...$$ است. نکته مهمی که وجود دارد این است که تبدیل موجک گسسته فقط در دو حوزه مقیاس و جابه‌جایی گسسته است و در حوزه زمان گسسته نیست. برای کار کردن با سیگنال‌های دیجیتال و گسسته، لازم است که تابع موجک را در حوزه زمان گسسته‌سازی کنیم. این فرم‌های تبدیل موجک را تبدیل موجک گسسته در زمان یا تبدیل موجک پیوسته گسسته در زمان می‌گویند.

تبدیل موجک گسسته به صورت بانک فیلتری

در عمل، تبدیل موجک گسسته به صورت یک بانک فیلتری پیاده‌سازی می‌شود، بدین معنی که به صورت دنباله‌ای از فیلترهای پایین گذر و بالا گذر عمل می‌کند، به این دلیل که استفاده از بانک فیلتری یک راه بسیار موثر برای تجزیه یک سیگنال به زیرباندهای فرکانسی (Frequency Sub-bands) متعدد است. تلاش داریم تا در ادامه مفهوم پنهان در بانک فیلتری را به صورت ساده توضیح دهیم. درک عملکرد بانک فیلتری برای درک عملکرد تبدیل موجک ضروری است و می‌تواند در کاربردهای مختلف مورد استفاده قرار گیرد.

برای اعمال تبدیل موجک گسسته بر روی یک سیگنال، ابتدا با مقیاس‌های کوچک شروع می‌کنیم. همان طور که قبلا گفتیم، مقیاس‌های کوچک متناظر با فرکانس‌های بالا است. بنابراین، ما ابتدا فرکانس‌های بالا را آنالیز می‌کنیم. در گام دوم، مقیاس را با فاکتور دو افزایش می‌دهیم (فرکانس را با فاکتور دو کاهش می‌دهیم.) و در این حالت رفتار را در اطراف نصف فرکانس بیشینه آنالیز می‌کنیم. در گام سوم، فاکتور مقیاس را برابر با ۴ در نظر می‌گیریم و ما رفتار فرکانسی را در اطراف ربع فرکانس بیشینه تحلیل می‌کنیم. این روال به همین ترتیب ادامه می‌یابد تا به بیشینه سطح تجزیه برسیم.

برای درک مفهوم بیشینه سطح تجزیه (Maximum Decomposition Level)، ابتدا باید بدانیم که در هر مرحله متوالی، تعداد نمونه‌ها در سیگنال با فاکتور دو کاهش می‌یابد. در مقادیر فرکانس‌های پایین، به نمونه‌های کمتری نیاز داریم تا در نرخ نمونه‌برداری نایکوئیست صدق کنند، بنابراین لازم نیست تعداد نمونه‌های بیشتری را در سیگنال حفظ کنیم؛ زیرا این کار تنها باعث می‌شود که هزینه محاسباتی بالاتر برود. به دلیل زیرنمونه‌برداری (Downsampling) در بعضی از گام‌های فرایند، تعداد نمونه‌ها در سیگنال از طول فیلتر موجک کوچک‌تر می‌شود و در این حالت به بیشینه سطح تجزیه می‌رسیم.

به عنوان مثال، فرض کنید که سیگنالی با فرکانس‌های در بازه 0 تا ۱۰۰۰ هرتز داریم. در گام اول، سیگنال را به دو بخش فرکانس بالا و فرکانس پایین تجزیه می‌کنیم. مثلا بخش اول فرکانس‌های ۰ تا ۵۰۰ هرتز و بخش دوم فرکانس‌های ۵۰۰ تا ۱۰۰۰ هرتز هستند. در گام دوم، بخش فرکانس پایین را در نظر می‌گیریم و مجددا آن را به دو بخش با فرکانس‌های ۰ تا ۲۵۰ هرتز و ۲۵۰ تا ۵۰۰ هرتز تقسیم می‌کنیم. در گام سوم، بخش ۰ تا ۲۵۰ هرتز را در نظر می‌گیریم و آن را به دو بخش ۰ تا ۱۲۵ هرتز و ۱۲۵ تا ۲۵۰ هرتز تقسیم می‌کنیم. این روند را به همین صورت تا زمانی ادامه می‌دهیم که یا به درجه پالایش مورد نیاز برسیم و یا تعداد نمونه‌ها تمام شود.

می‌توان این ایده را به سادگی با استفاده از قطعه کد زیر به صورت تصویری نشان داد. در این کد نشان می‌دهیم که با اعمال تبدیل موجک گسسته روی یک سیگنال چیرپ (Chirp Signal)، چه اتفاقی رخ می‌دهد. سیگنال چیرپ، سیگنالی است که دارای طیف فرکانسی دینامیک باشد. در واقع طیف فرکانسی با زمان افزایش می‌یابد، سیگنال در ابتدا دارای مقادیر فرکانس پایین است و هر چه به سمت آخر سیگنال پیش می‌رویم، مقادیر سیگنال فرکانس بالاتر می‌شوند.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

استفاده از سیگنال چیرپ، مصورسازی این‌که کدام بخش از طیف فرکانسی فیلتر شده‌ است را از طریق نگاه کردن به محور زمان، ساده‌تر می‌کند.

1import pywt
2
3x = np.linspace(0, 1, num=2048)
4chirp_signal = np.sin(250 * np.pi * x**2)
5    
6fig, ax = plt.subplots(figsize=(6,1))
7ax.set_title("Original Chirp Signal: ")
8ax.plot(chirp_signal)
9plt.show()
10    
11data = chirp_signal
12waveletname = 'sym5'
13
14fig, axarr = plt.subplots(nrows=5, ncols=2, figsize=(6,6))
15for ii in range(5):
16    (data, coeff_d) = pywt.dwt(data, waveletname)
17    axarr[ii, 0].plot(data, 'r')
18    axarr[ii, 1].plot(coeff_d, 'g')
19    axarr[ii, 0].set_ylabel("Level {}".format(ii + 1), fontsize=14, rotation=90)
20    axarr[ii, 0].set_yticklabels([])
21    if ii == 0:
22        axarr[ii, 0].set_title("Approximation coefficients", fontsize=14)
23        axarr[ii, 1].set_title("Detail coefficients", fontsize=14)
24    axarr[ii, 1].set_yticklabels([])
25plt.tight_layout()
26plt.show()

در تصویر زیر نمایی از نحوه عملکرد تبدیل موجک گسسته به عنوان بانک فیلتری و خروجی قطعه کد بالا را می‌توان دید.

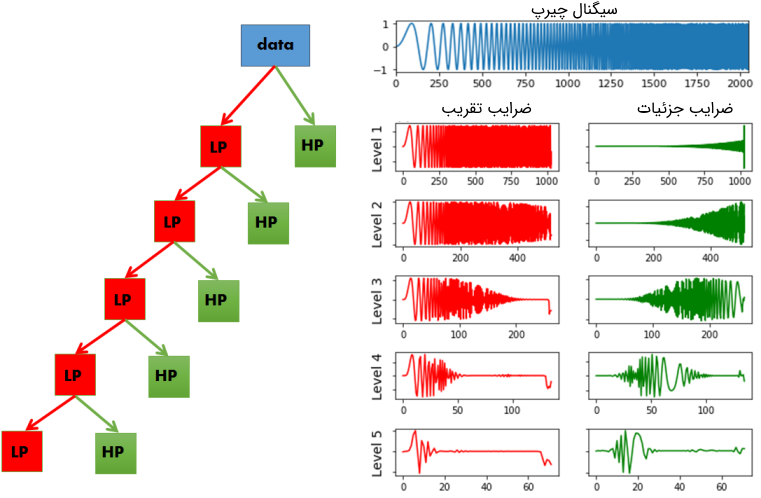
در تصویر بالا می‌توان سیگنال چیرپ و تبدیل موجک گسسته اعمال شده به آن را مشاهده کرد. در رابطه با این تبدیل ذکر چند نکته اهمیت بالایی دارد.

• در کتابخانه PyWavelets، تبدیل موجک گسسته توسط دستور pywt.dwt()‎ اعمال می‌شود.
• تبدیل موجک گسسته دو مجموعه از ضرایب را به عنوان خروجی باز می‌گرداند، ضرایب تقریب (Approximation Coefficients) و ضرایب جزئیات (Detail Coefficients).
• ضرایب تقریب نشان‌دهنده خروجی فیلتر پایین‌گذر (فیلتر میانگین‌گیر) در تبدیل موجک گسسته هستند.
• ضرایب جزئیات نشان‌دهنده خروجی فیلتر بالاگذر (فیلتر مشتق‌گیر) در تبدیل موجک گسسته هستند.
• با اعمال تبدیل موجک گسسته مجددا روی ضرایب تقریب تبدیل موجک قبلی، تبدیل موجک مربوط به مرحله بعد را به دست می‌آوریم.
• در هر گام، نمونه‌برداری سیگنال اصلی با فاکتور دو کاهش می‌یابد.

حال می‌توان درک کرد که چرا تبدیل موجک گسسته به صورت بانک فیلتری پیاده‌سازی می‌شود. در هر مرحله متوالی، ضرایب تقریب به دو بخش پایین‌گذر و بالاگذر تقسیم می‌شوند و در مرحله بعد، تبدیل موجک مجددا روی بخش پایین‌گذر اعمال می‌شود. همان طور که می‌توان دید، سیگنال اصلی ما در حال حاضر به سیگنال‌های متعددی تبدیل شده است که هر کدام متناظر با باندهای فرکانسی مختلفی هستند. بعدا خواهیم دید که ضرایب تقریب و جزئی در زیر باندهای مختلف چگونه در کاربردهایی مانند حذف نویزهای فرکانس بالا از سیگنال‌ها، فشرده کردن سیگنال‌ها و یا طبقه‌بندی (Classifying) انواع مختلف سیگنال‌ها مورد استفاده قرار می‌گیرند.

همچنین می‌توانیم از دستور pywt.wavedec برای محاسبه سریع ضرایب از مرتبه بالاتر استفاده کرد. این دستور تابع اصلی و مرتبه n را به عنوان ورودی دریافت می‌کند و یک مجموعه از ضرایب تقریب (از مرتبه n) و n مجموعه از ضرایب جزئیات (از مرتبه یک تا n) را به عنوان خروجی باز می‌گرداند.

ایده آنالیز سیگنال با مقیاس‌های متفاوت را آنالیز چند-رزولوشنی (Multiresolution) یا چند-مقیاسی (Multiscale) می‌گویند و تجزیه سیگنال به این روش را نیز تجزیه چندرزولوشنی یا کدینگ زیرباند (Sub-Band Coding) می گویند.

مصورسازی فضای حالت با استفاده از تبدیل موجک پیوسته

تا این قسمت با مفهوم تبدیل موجک، تفاوت آن با تبدیل فوریه، تفاوت بین تبدیل موجک پیوسته و تبدیل موجک گسسته، انواع خانواده‌های مختلف تبدیل موجک، تاثیر درجه و سطح تجزیه روی موجک مادر آشنا شدیم و دانستیم چرا و چگونه تبدیل موجک گسسته مانند بانک فیلتری عمل می‌کند. همچنین دیدیم که خروجی تبدیل موجک روی سیگنال یک بعدی، منتج به یک اسپکتروگرام دو بعدی می‌شود. این اسپکتروگرام می‌تواند اطلاعات جزئی را درباره فضای حالت سیستم در اختیار ما قرار دهد یا به عبارت دیگر اطلاعاتی راجع به رفتار دینامیک سیستم در خود دارد.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

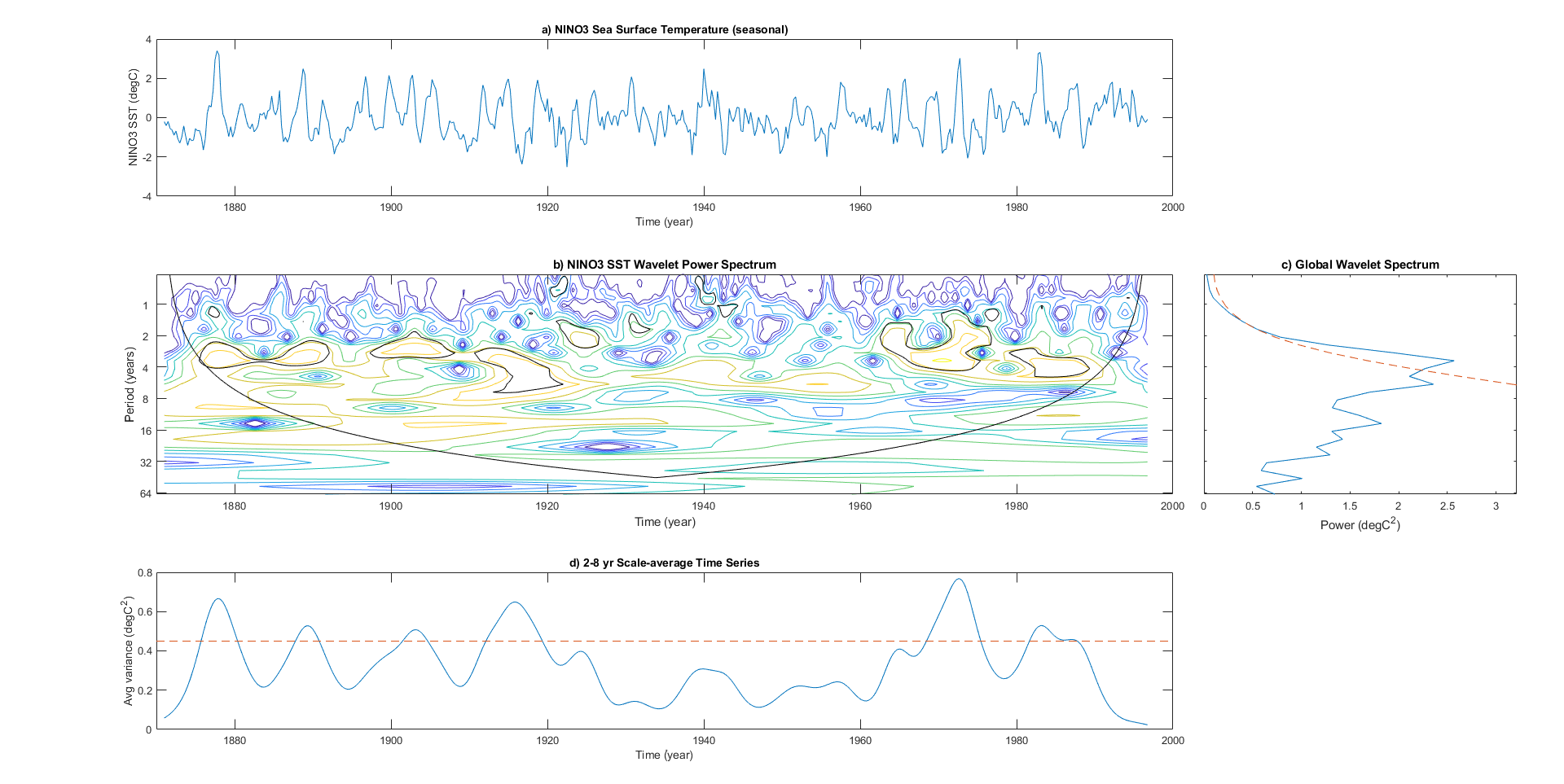
دیتاست el-Nino یک سری زمانی است که برای ردیابی پدیده ال نینو مورد استفاده قرار می‌گیرد. این دیتاست شامل اندازه گیری‌های سه ماهه دمای سطح دریا از سال 1871 تا 1997 است. به منظور درک قدرت یک اسپکتروگرام، می‌خواهیم تبدیل موجک را برای داده‌های دیتاست ال نینو همراه با داده‌های سری زمانی واقعی و تبدیل فوریه آن‌ها نشان دهیم. این کار را با استفاده از قطعه کد زیر انجام می‌دهیم.

1def plot_wavelet(time, signal, scales, 
2                 waveletname = 'cmor', 
3                 cmap = plt.cm.seismic, 
4                 title = 'Wavelet Transform (Power Spectrum) of signal', 
5                 ylabel = 'Period (years)', 
6                 xlabel = 'Time'):
7    
8    dt = time[1] - time[0]
9    [coefficients, frequencies] = pywt.cwt(signal, scales, waveletname, dt)
10    power = (abs(coefficients)) ** 2
11    period = 1. / frequencies
12    levels = [0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 8]
13    contourlevels = np.log2(levels)
14    
15    fig, ax = plt.subplots(figsize=(15, 10))
16    im = ax.contourf(time, np.log2(period), np.log2(power), contourlevels, extend='both',cmap=cmap)
17    
18    ax.set_title(title, fontsize=20)
19    ax.set_ylabel(ylabel, fontsize=18)
20    ax.set_xlabel(xlabel, fontsize=18)
21    
22    yticks = 2**np.arange(np.ceil(np.log2(period.min())), np.ceil(np.log2(period.max())))
23    ax.set_yticks(np.log2(yticks))
24    ax.set_yticklabels(yticks)
25    ax.invert_yaxis()
26    ylim = ax.get_ylim()
27    ax.set_ylim(ylim[0], -1)
28    
29    cbar_ax = fig.add_axes([0.95, 0.5, 0.03, 0.25])
30    fig.colorbar(im, cax=cbar_ax, orientation="vertical")
31    plt.show()
32
33def plot_signal_plus_average(time, signal, average_over = 5):
34    fig, ax = plt.subplots(figsize=(15, 3))
35    time_ave, signal_ave = get_ave_values(time, signal, average_over)
36    ax.plot(time, signal, label='signal')
37    ax.plot(time_ave, signal_ave, label = 'time average (n={})'.format(5))
38    ax.set_xlim([time[0], time[-1]])
39    ax.set_ylabel('Signal Amplitude', fontsize=18)
40    ax.set_title('Signal + Time Average', fontsize=18)
41    ax.set_xlabel('Time', fontsize=18)
42    ax.legend()
43    plt.show()
44    
45def get_fft_values(y_values, T, N, f_s):
46    f_values = np.linspace(0.0, 1.0/(2.0*T), N//2)
47    fft_values_ = fft(y_values)
48    fft_values = 2.0/N * np.abs(fft_values_[0:N//2])
49    return f_values, fft_values
50
51def plot_fft_plus_power(time, signal):
52    dt = time[1] - time[0]
53    N = len(signal)
54    fs = 1/dt
55    
56    fig, ax = plt.subplots(figsize=(15, 3))
57    variance = np.std(signal)**2
58    f_values, fft_values = get_fft_values(signal, dt, N, fs)
59    fft_power = variance * abs(fft_values) ** 2     # FFT power spectrum
60    ax.plot(f_values, fft_values, 'r-', label='Fourier Transform')
61    ax.plot(f_values, fft_power, 'k--', linewidth=1, label='FFT Power Spectrum')
62    ax.set_xlabel('Frequency [Hz / year]', fontsize=18)
63    ax.set_ylabel('Amplitude', fontsize=18)
64    ax.legend()
65    plt.show()
66
67dataset = "http://paos.colorado.edu/research/wavelets/wave_idl/sst_nino3.dat"
68df_nino = pd.read_table(dataset)
69N = df_nino.shape[0]
70t0=1871
71dt=0.25
72time = np.arange(0, N) * dt + t0
73signal = df_nino.values.squeeze()
74
75scales = np.arange(1, 128)
76plot_signal_plus_average(time, signal)
77plot_fft_plus_power(time, signal)
78plot_wavelet(time, signal, scales)

نتیجه اجرای این کد تصاویر زیر است که می‌توانید آن‌ها را مشاهده کنید.

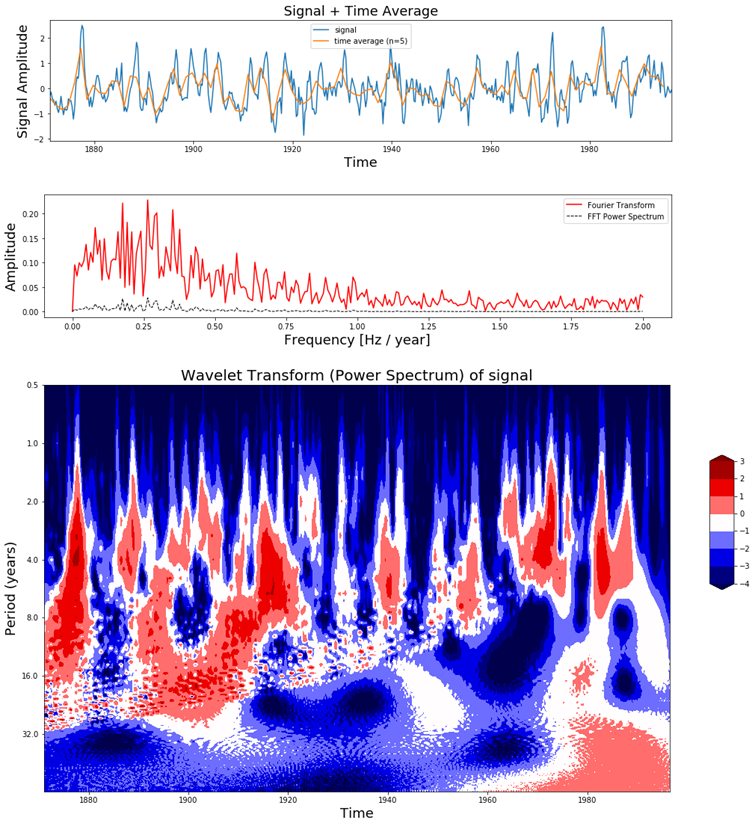
با دقت در تصویر بالا می‌توان دید که در اولین نمودار، سری زمانی دیتاست ال نینو به همراه میانگین زمانی آن نشان داده شده است. در تصویر وسط، تبدیل فوریه سری زمانی و در تصویر سوم، اسپکتروگرام این سیگنال را که از طریق تبدیل موجک پیوسته سیگنال اصلی به دست آمده است، می‌توان مشاهده کرد.

در این اسپکتروگرام می‌توان دید که قسمت عمده توان در یک دوره ۲ تا ۸ ساله متمرکز شده است. اگر این دوره را از طریق فرمول $$T = \frac{1} {f }$$ به فرکانس تبدیل کنیم، آن‌گاه به بازه فرکانس ۰٫۱۲۵ هرتز تا ۰٫۵ هرتز خواهیم رسید. البته از روی نمودار تبدیل فوریه نیز می‌توان افزایش توان در اطراف این فرکانس‌ها را مشاهده کرد. اما تفاوت اصلی که نمودار تبدیل فوریه و نمودار تبدیل موجک با یکدیگر دارند، در این است که تبدیل موجک می‌تواند اطلاعات زمانی را نیز در اختیار ما قرار دهد، در حالی که نمودار تبدیل فوریه این توانایی را ندارد.

به عنوان مثال، در اسپکتروگرام می‌توان دید که تا سال ۱۹۲۰ نوسانات بسیاری در تغییرات دما وجود دارد، در حالی که بین سال‌های ۱۹۶۰ تا ۱۹۹۰ نوسانات به این شدت نیستند. همچنین می‌توان دید که با پیشرفت زمان، یک انتقال از تناوب‌های کوتاه به تناوب‌های بلند به وجود آمده است. در واقع، این یک نوع رفتار دینامیک در سیستم است که می‌توان با استفاده از تبدیل موجک به وجود آن پی برد، در حالی که تبدیل فوریه قادر به آشکارسازی رفتارهای دینامیک یک سیگنال نخواهد بود. اکنون واضح‌تر شده است که تبدیل موجک در کاربردهای پردازش سیگنال و یادگیری ماشین تا چه اندازه قدرتمندتر عمل می‌کند. برای کامل‌تر شدن بحث، می‌خواهیم به نحوه کاربرد تبدیل موجک به همراه شبکه عصبی کانولوشنی در طبقه‌بندی یک سیگنال بپردازیم.

استفاده از تبدیل موجک در طبقه‌بندی سیگنال

همان طور که گفتیم، تبدیل موجک یک سیگنال یک بعدی، یک اسپکتروگرام دو بعدی خواهد بود که حاوی اطلاعات بیشتری نسبت به سیگنال سری زمانی و یا تبدیل فوریه آن است. این حقیقت را با اعمال تبدیل موجک بر روی دیتاست ال نینو مشاهده کردیم. با اعمال تبدیل موجک روی این دیتاست، نه تنها به اطلاعات دوره تناوب بزرگترین نوسانات در دمای سطح دریا پی می‌بریم، بلکه خواهیم دانست این نوسانات چه زمانی رخ داده‌اند و چه زمانی وجود نداشته‌اند.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

این اسپکتروگرام، برای درک بهتر رفتر دینامیک یک سیگنال مورد استفاده قرار می‌گیرد و نیز با استفاده از آن می‌توان انواع مختلف سیگنال‌های تولید شده توسط یک سیستم را از یکدیگر تمایز داد. اگر یک سیگنال حیاتی بدن را هنگام بالا رفتن از پله‌ها و نیز پایین رفتن از پله ها ضبط کنید، اسپکتروگرام سیگنال در این دو حالت با یکدیگر تفاوت خواهند داشت. به همین ترتیب سیگنال‌های الکتروکاردیوگرافی (ECG) افراد سالم با سیگنال‌های ECG افراد آریتمی مختلف خواهد بود. از این ویژگی می‌توان در تشخیص عیب (Fault Detection) ادوات و دستگاه‌های مکانیکی مانند موتورها و توربین‌های بادی نیز می‌توان استفاده کرد.

بنابراین با نگاه کردن به اسپکتروگرام، می‌توان یک روتور موتور معیوب را از یک روتور سالم یا یک فرد سالم از فرد بیمار و یا بالا رفتن از پله را از پایین رفتن از آن تشخیص داد. اما گاهی لازم است که این کار را بدون چک کردن دستی اسپکتروگرام‌های متعدد مربوط به موارد مختلف انجام دهیم. یک راه برای انجام اتوماتیک این کار، ایجاد یک شبکه عصبی کانولوشنی است. این شبکه عصبی قادر است که به صورت خودکار، کلاسی که اسپکتروگرام به آن تعلق دارد را مشخص کند و در نتیجه سیگنال‌ها را بر اساس آن طبقه‌بندی کند. اگر با شبکه عصبی کانولوشن آشنا نیستید، بهتر است که ابتدا مطلب «بررسی شبکه عصبی کانولوشن (CNN)» را در مجله فرادرس مطالعه کنید. در بخش‌های بعد، ابتدا یک دیتاست را بارگذاری می‌کنیم که اطلاعات افراد در حین انجام شش فعالیت مختلف را ضبط کرده است. سپس اسپکتروگرام این دیتاست را با استفاده از تبدیل موجک ترسیم می‌کنیم و در نهایت با استفاده از شبکه عصبی کانولوشنی این سیگنال‌ها را طبقه‌بندی خواهیم کرد.

بارگذاری دیتاست

حال می‌خواهیم داده‌های یک دیتاست شامل سری زمان را با استفاده از اسپکتروگرام و شبکه CNN طبقه‌بندی کنیم. ابتدا دیتاست تشخیص فعالیت‌های انسان (UCI-HAR) را از این لینک دانلود و سپس بارگذاری می‌کنیم. این دیتاست با استفاده از سنسورها از افراد در حال انجام کارهای مختلف مانند بالا و پایین رفتن از پله، خوابیدن، ایستادن و راه رفتن ضبط شده است. در کل، 10000 سیگنال در این دیتاست قرار دارد که هر کدام از آن‌ها از ۹ المان تشکیل شده‌اند.

بعد از اینکه دیتاست را دانلود کردیم، می‌توانیم آن را با کد زیر در یک nd-array از کتابخانه numpy بارگذاری کرد.

1def read_signals_ucihar(filename):
2    with open(filename, 'r') as fp:
3        data = fp.read().splitlines()
4        data = map(lambda x: x.rstrip().lstrip().split(), data)
5        data = [list(map(float, line)) for line in data]
6    return data
7
8def read_labels_ucihar(filename):        
9    with open(filename, 'r') as fp:
10        activities = fp.read().splitlines()
11        activities = list(map(int, activities))
12    return activities
13
14def load_ucihar_data(folder):
15    train_folder = folder + 'train/InertialSignals/'
16    test_folder = folder + 'test/InertialSignals/'
17    labelfile_train = folder + 'train/y_train.txt'
18    labelfile_test = folder + 'test/y_test.txt'
19    train_signals, test_signals = [], []
20    for input_file in os.listdir(train_folder):
21        signal = read_signals_ucihar(train_folder + input_file)
22        train_signals.append(signal)
23    train_signals = np.transpose(np.array(train_signals), (1, 2, 0))
24    for input_file in os.listdir(test_folder):
25        signal = read_signals_ucihar(test_folder + input_file)
26        test_signals.append(signal)
27    test_signals = np.transpose(np.array(test_signals), (1, 2, 0))
28    train_labels = read_labels_ucihar(labelfile_train)
29    test_labels = read_labels_ucihar(labelfile_test)
30    return train_signals, train_labels, test_signals, test_labels
31
32folder_ucihar = './data/UCI_HAR/' 
33train_signals_ucihar, train_labels_ucihar, test_signals_ucihar, test_labels_ucihar = load_ucihar_data(folder_ucihar)

داده‌های آموزش (Training Set) شامل 7352 سیگنال هستند که هر سیگنال ۱۲۸ نمونه اندازه‌گیری و 9 المان دارد. بنابراین داده‌های آموزش در یک ndarray با ابعاد $$(7352, 128, 9)$$ و داده‌های تست (Test Set) در یک آرایه دیگر با ابعاد $$(2947, 128, 9)$$ بارگذاری می‌کنیم.

چون هر سیگنال از ۹ المان تشکیل شده است، در نتیجه باید تبدیل موجک پیوسته را به هر سیگنال ۹ بار اعمال کنیم. در تصویر زیر نتیجه حاصل از اعمال تبدیل موجک پیوسته به دو سیگنال مختلف از دیتاست را می‌توان مشاهده کرد.

در تصویر بالا، نمونه‌های حاصل از اعمال تبدیل موجک به یک سیگنال فرد در حال بالا رفتن از پله‌ها و فرد خوابیده را می‌توان مشاهده کرد.

اعمال تبدیل موجک پیوسته بر روی دیتاست

چون هر سیگنال دارای ۹ مولفه است، بنابراین هر سیگنال ۹ اسپکتروگرام نیز دارد. بنابراین سوال بعدی این است که چگونه این ۹ اسپکتروگرام را به شبکه کانولوشنی وارد کنیم. راه‌های مختلفی برای این کار وجود دارد.

فیلم آموزش آشنایی با پردازش سیگنال های دیجیتال در متلب MATLAB در فرادرس

کلیک کنید

1. راه اول این است که برای هر مولفه، یک شبکه CNN را به صورت جداگانه آموزش دهیم و سپس نتایج این ۹ شبکه را از طریق یکی از روش‌های Ensembling با یکدیگر مخلوط کنیم. اما این روش در حالت کلی منجر به نتایج ضعیفی می‌شود؛ زیرا وابستگی‌های داخلی بین این ۹ مولفه را در شبکه عصبی دخالت نداده‌ایم.
2. راه دوم الحاق کردن (Concatenate) این ۹ سیگنال مختلف به یکدیگر و ایجاد یک سیگنال طولانی‌تر و سپس اعمال شبکه عصبی به سیگنال الحاقی است. این روش نیز می‌تواند کارا باشد، اما در محل الحاق سیگنال‌ها به یکدیگر، شاهد ناپیوستگی‌هایی خواهیم بود. این ناپیوستگی‌ها می‌توانند در محل مرزهای مولفه‌های سیگنال‌ در اسپکتروگرام منجر به ایجاد نویز شوند.
3. راه سوم این است که ابتدا تبدیل موجک پیوسته را محاسبه کنیم و سپس ۹ تصویر تبدیل موجک مختلف را به یکدیگر الحاق کنیم و تصویر نهایی را به شبکه عصبی وارد کنیم. این روش نیز موثر است، اما در آن نیز مجددا در لبه‌های تصاویر تبدیل موجک، ناپیوستگی به وجود می‌آید که باعث ایجاد نویز می‌شود و در نهایت وارد شبکه عصبی می‌شود. اگر شبکه عصبی کانولوشنی به اندازه کافی عمیق باشد، آن‌گاه قادر خواهد بود که تفاوت بین این قسمت‌های نویزی و قسمت‌های مفید و واقعی تصویر را تشخیص دهد. با این وجود، استفاده از راه حل چهارم پیشنهاد می‌شود.
4. هر ۹ اسپکتروگرام را روی (Top) یکدیگر قرار دهید و یک تصویر با ۹ کانال مختلف را ایجاد کنید.

اما تصویری با ۹ کانال به چه معنی است؟ در حالت عادی، هر تصویر یا سیاه و سفید است و یک کانال دارد و یا تصویر از نوع رنگی (RGB) بوده و سه کانال دارد. اما شبکه عصبی کانولوشنی برای سادگی در مدیریت تصاویر می‌تواند این تصاویر مختلف را در کنار یکدیگر و به عنوان ۹ کانال در نظر بگیرد. طریقه عملکرد شبکه عصبی CNN همچنان مانند قبل است، اما تفاوتی که وجود دارد این است که در مقایسه با یک تصویر RGB، سه برابر فیلتر بیشتری وجود خواهد داشت. در تصویر زیر روند انجام این کار را می‌توان مشاهده کرد.

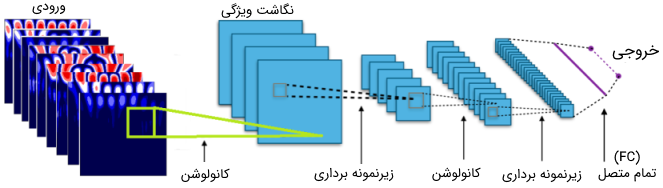
در تصویر بالا نشان داده شده است که چگونه از ۹ تصویر حاصل از اعمال تبدیل موجک به ۹ مولفه سیگنال، برای ایجاد یک تصویر ۹ کانالی برای ورودی شبکه کانولوشنی استفاده شده است.

در ادامه، قطعه کد پایتون مربوط به اعمال تبدیل موجک پیوسته روی سیگنال‌های دیتاست و نیز بازآرایی مجدد آن‌ها برای کاربرد در ورودی شبکه عصبی کانولوشنی را مشاهده می‌کنید. دیتاست در حالت کلی شامل ۱۰۰۰۰ سیگنال است، اما در اینجا از ۵۰۰۰ سیگنال به عنوان داده آموزش و از ۵۰۰ سیگنال دیگر به عنوان داده تست استفاده می‌کنیم.

1scales = range(1,128)
2waveletname = 'morl'
3train_size = 5000
4test_size= 500
5
6train_data_cwt = np.ndarray(shape=(train_size, 127, 127, 9))
7
8for ii in range(0,train_size):
9    if ii % 1000 == 0:
10        print(ii)
11    for jj in range(0,9):
12        signal = uci_har_signals_train[ii, :, jj]
13        coeff, freq = pywt.cwt(signal, scales, waveletname, 1)
14        coeff_ = coeff[:,:127]
15        train_data_cwt[ii, :, :, jj] = coeff_
16
17test_data_cwt = np.ndarray(shape=(test_size, 127, 127, 9))
18for ii in range(0,test_size):
19    if ii % 100 == 0:
20        print(ii)
21    for jj in range(0,9):
22        signal = uci_har_signals_test[ii, :, jj]
23        coeff, freq = pywt.cwt(signal, scales, waveletname, 1)
24        coeff_ = coeff[:,:127]
25        test_data_cwt[ii, :, :, jj] = coeff_
26
27uci_har_labels_train = list(map(lambda x: int(x) - 1, uci_har_labels_train))
28uci_har_labels_test = list(map(lambda x: int(x) - 1, uci_har_labels_test))
29
30x_train = train_data_cwt
31y_train = list(uci_har_labels_train[:train_size])
32x_test = test_data_cwt
33y_test = list(uci_har_labels_test[:test_size])

همان طور که از قطعه کد بالا مشخص است، تبدیل موجک یک مولفه تکی سیگنال (۱۲۸ نمونه) منجر به یک تصویر با ابعاد ۱۲۷ در ۱۲۷ پیکسل می‌شود، بنابراین اسپکتروگرام حاصل از ۵۰۰۰ داده آموزش، در یک آرایه با ابعاد $$(5000, 127, 127, 9)$$ ذخیره می‌شود. همچنین اسپکتروگرام حاصل از ۵۰۰ سیگنال تست، در آرایه numpy دیگری با ابعاد $$(500, 127, 127, 9)$$ ذخیره‌سازی می‌شود.

آموزش شبکه عصبی کانولوشنی

حال که داده‌ها در فرمت صحیحی قرار گرفته‌اند، می‌توان شبکه عصبی CNN را آموزش داد. برای این قسمت لازم است تا از کتابخانه Keras استفاده کنیم. بنابراین باید ابتدا آن را نصب کنیم.

فیلم آموزش مقدماتی پردازش سیگنال با پایتون Python در فرادرس

کلیک کنید

در ادامه کدهای پایتون برای آموزش شبکه عصبی آورده شده‌اند:

1import keras
2from keras.layers import Dense, Flatten
3from keras.layers import Conv2D, MaxPooling2D
4from keras.models import Sequential
5from keras.callbacks import History 
6history = History()
7
8img_x = 127
9img_y = 127
10img_z = 9
11input_shape = (img_x, img_y, img_z)
12
13num_classes = 6
14batch_size = 16
15num_classes = 7
16epochs = 10
17
18x_train = x_train.astype('float32')
19x_test = x_test.astype('float32')
20
21y_train = keras.utils.to_categorical(y_train, num_classes)
22y_test = keras.utils.to_categorical(y_test, num_classes)
23
24
25model = Sequential()
26model.add(Conv2D(32, kernel_size=(5, 5), strides=(1, 1),
27                 activation='relu',
28                 input_shape=input_shape))
29model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
30model.add(Conv2D(64, (5, 5), activation='relu'))
31model.add(MaxPooling2D(pool_size=(2, 2)))
32model.add(Flatten())
33model.add(Dense(1000, activation='relu'))
34model.add(Dense(num_classes, activation='softmax'))
35
36model.compile(loss=keras.losses.categorical_crossentropy,
37              optimizer=keras.optimizers.Adam(),
38              metrics=['accuracy'])
39
40
41model.fit(x_train, y_train,
42          batch_size=batch_size,
43          epochs=epochs,
44          verbose=1,
45          validation_data=(x_test, y_test),
46          callbacks=[history])
47
48train_score = model.evaluate(x_train, y_train, verbose=0)
49print('Train loss: {}, Train accuracy: {}'.format(train_score[0], train_score[1]))
50test_score = model.evaluate(x_test, y_test, verbose=0)
51print('Test loss: {}, Test accuracy: {}'.format(test_score[0], test_score[1]))
52
53*** Epoch 1/10
54*** 5000/5000 [==============================] - 235s 47ms/step - loss: 0.3963 - acc: 0.8876 - val_loss: 0.6006 - val_acc: 0.8780
55*** Epoch 2/10
56*** 5000/5000 [==============================] - 228s 46ms/step - loss: 0.1939 - acc: 0.9282 - val_loss: 0.3952 - val_acc: 0.8880
57*** Epoch 3/10
58*** 5000/5000 [==============================] - 224s 45ms/step - loss: 0.1347 - acc: 0.9434 - val_loss: 0.4367 - val_acc: 0.9100
59*** Epoch 4/10
60*** 5000/5000 [==============================] - 228s 46ms/step - loss: 0.1971 - acc: 0.9334 - val_loss: 0.2662 - val_acc: 0.9320
61*** Epoch 5/10
62*** 5000/5000 [==============================] - 231s 46ms/step - loss: 0.1134 - acc: 0.9544 - val_loss: 0.2131 - val_acc: 0.9320
63*** Epoch 6/10
64*** 5000/5000 [==============================] - 230s 46ms/step - loss: 0.1285 - acc: 0.9520 - val_loss: 0.2014 - val_acc: 0.9440
65*** Epoch 7/10
66*** 5000/5000 [==============================] - 232s 46ms/step - loss: 0.1339 - acc: 0.9532 - val_loss: 0.2884 - val_acc: 0.9300
67*** Epoch 8/10
68*** 5000/5000 [==============================] - 237s 47ms/step - loss: 0.1503 - acc: 0.9488 - val_loss: 0.3181 - val_acc: 0.9340
69*** Epoch 9/10
70*** 5000/5000 [==============================] - 250s 50ms/step - loss: 0.1247 - acc: 0.9504 - val_loss: 0.2403 - val_acc: 0.9460
71*** Epoch 10/10
72*** 5000/5000 [==============================] - 238s 48ms/step - loss: 0.1578 - acc: 0.9508 - val_loss: 0.2133 - val_acc: 0.9300
73*** Train loss: 0.11115437872409821, Train accuracy: 0.959
74*** Test loss: 0.21326758581399918, Test accuracy: 0.93

دقت طبقه‌بندی دیتاست UCI-HAR با استفاده از ترکیب شبکه عصبی کانولوشنی و تبدیل موجک را روی داده‌های آموزش و تست می توان در تصویر زیر مشاهده کرد.

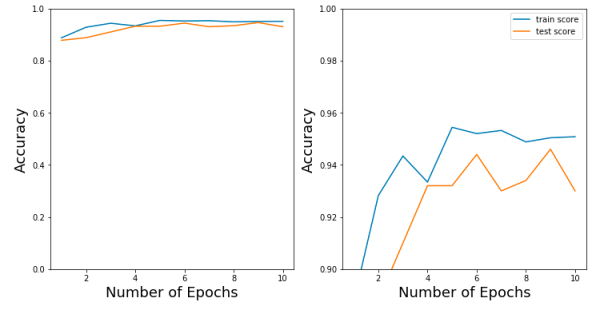
همان طور که می‌توان دید، تلفیق تبدیل موجک و شبکه عصبی کانولوشنی منجر به نتایج فوق‌العاده‌ای می‌شود. در طبقه‌بندی انواع مختلف فعالیت‌های انسان، استفاده از این روش منجر به 94 درصد دقت (Accuracy) می‌شود. این دقت بسیار بالاتر از دقتی است که با سایر روش‌های طبقه‌بندی می‌توان به آن رسید. در بخش بعد، از تبدیل فوریه گسسته استفاده می‌کنیم و مجددا داده‌های همین دیتاست را طبقه‌بندی می‌کنیم و نتایج را در دو حالت با یکدیگر مقایسه می‌کنیم.

تجزیه سیگنال با استفاده از تبدیل موجک گسسته

در بخش‌های قبلی دیدیم که چگونه تبدیل موجک گسسته مانند یک بانک فیلتری عمل می‌کند و می‌تواند یک سیگنال را به فرکانس‌های زیر باند تجزیه کند. در این بخش، می‌خواهیم نحوه تجزیه یک سیگنال به فرکانس‌های زیر باند و بازسازی مجدد سیگنال اصلی را با استفاده از کتابخانه PyWavelets در پایتون بررسی کنیم. PyWavelets دو روش اساسی برای تجزیه یک سیگنال در اختیار کاربر قرار می‌دهد.

فیلم آموزش مقدماتی پردازش سیگنال با پایتون Python در فرادرس

کلیک کنید

1. در روش اول می‌توان pywt.dwt()‎ را روی سیگنال اعمال کرد و ضرایب تقریب را بازیابی کرد. سپس باید تبدیل موجک گسسته را روی ضرایب بازیابی شده اعمال کرد تا ضرایب مرحله دوم را به دست آورد. این فرایند را باید تا رسیدن به سطح تجزیه مطلوب ادامه داد.
2. در روش دوم، می‌توان تابع pywt.wavedec()‎ را مستقیما روی سیگنال اعمال کرد و تمام ضرایب جزئیات را تا سطح تجزیه دلخواه n به دست آورد. این تابع، سیگنال اصلی و سطح n را به عنوان ورودی دریافت می‌کند و یک مجموعه از ضرایب تقریب (مربوط به سطح تجزیه n) و n مجموعه از ضرایب جزئیات (از سطح یک تا سطح n) را در خروجی باز می‌گرداند.

با استفاده از قطعه کد زیر می‌توان نتیجه استفاده از روش اول را بررسی کرد.

1(cA1, cD1) = pywt.dwt(signal, 'db2', 'smooth')
2reconstructed_signal = pywt.idwt(cA1, cD1, 'db2', 'smooth')
3
4fig, ax = plt.subplots(figsize=(8,4))
5ax.plot(signal, label='signal')
6ax.plot(reconstructed_signal, label='reconstructed signal', linestyle='--')
7ax.legend(loc='upper left')
8plt.show()

در تصویر زیر به عنوان خروجی می‌توان سیگنال اصلی را به همراه سیگنال بازسازی شده مشاهده کرد.

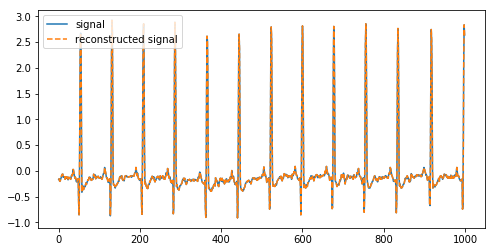
در تصویر بالا، یک سیگنال را به ضرایب آن تجزیه کردیم و مجددا با استفاده از معکوس تبدیل موجک گسسته بازسازی نمودیم.

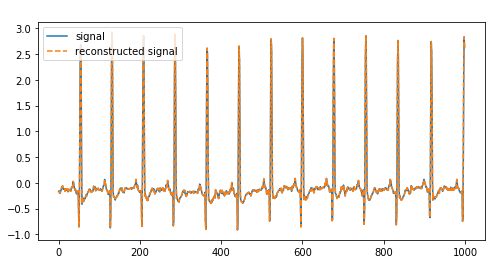
در روش دوم، از تابع pywt.wavedec()‎ استفاده می‌شود تا یک سیگنال را تجزیه و سپس مجددا بازسازی کرد. روش دوم ساده‌ترین راه برای تجزیه و بازسازی یک سیگنال است، مخصوصا زمانی که بخواهید ضرایب مرتبه بالاتر را به دست آورید. قطعه کد زیر نحوه استفاده از این تابع را نشان می‌دهد.

1coeffs = pywt.wavedec(signal, 'db2', level=8)
2reconstructed_signal = pywt.waverec(coeffs, 'db2')
3
4fig, ax = plt.subplots(figsize=(8,4))
5ax.plot(signal[:1000], label='signal')
6ax.plot(reconstructed_signal[:1000], label='reconstructed signal', linestyle='--')
7ax.legend(loc='upper left')
8ax.set_title('de- and reconstruction using wavedec()')
9plt.show()

خروجی این کد به صورت تصویر زیر است که سیگنال تجزیه شده و سیگنال بازسازی شده را با یکدیگر نشان می‌دهد.

حذف نویز (مولفه‌های فرکانس بالا) با استفاده از تبدیل موجک گسسته

در بخش قبل دیدیم که چگونه می‌توان یک سیگنال را به ضرایب تقریب (پایین گذر) و ضرایب جزئیات (بالا گذر) تجزیه کرد. اگر سیگنال را با استفاده از این ضرایب بازسازی کنیم، در نهایت سیگنال اصلی را می‌توان مجددا به دست آورد. اما اگر تعدادی از ضرایب جزئیات را از دست بدهیم، آن‌گاه در بازسازی سیگنال اصلی چه اتفاقی می‌افتد؟ به دلیل این‌که ضرایب جزئیات، نشان‌دهنده قسمت فرکانس بالا در سیگنال هستند، در نتیجه می‌توان گفت که در اثر حذف تعدادی از ضرایب جزئیات، بخشی از طیف فرکانسی فیلتر می‌شود. اگر در سیگنال نویزهای فرکانس بالای زیادی وجود داشته باشند، این روش می‌تواند به فیلتر و حذف کردن آن‌ها کمک کند.

صرف نظر کردن از ضرایب جزئیات، با استفاده از دستور pywt.threshold()‎ انجام می‌گیرد. در واقع این دستور مقادیر ضرایب بالاتر از حد آستانه (Threshold) خاصی را حذف می‌کند.

حال می‌خواهیم با استفاده از دیتاست «NASA’s Femto Bearing Dataset» این مفهوم را نشان دهیم. این دیتاست شامل داده‌های فرکانس بالای سنسور در حضور عیب یاتاقان (Bearings) است.

فیلم آموزش مقدماتی پردازش سیگنال با پایتون Python در فرادرس

کلیک کنید

قطعه کد زیر را در محیط پایتون اجرا می‌کنیم.

1DATA_FOLDER = './FEMTO_bearing/Training_set/Bearing1_1/'
2filename = 'acc_01210.csv'
3df = pd.read_csv(DATA_FOLDER + filename, header=None)
4signal = df[4].values
5
6def lowpassfilter(signal, thresh = 0.63, wavelet="db4"):
7    thresh = thresh*np.nanmax(signal)
8    coeff = pywt.wavedec(signal, wavelet, mode="per" )
9    coeff[1:] = (pywt.threshold(i, value=thresh, mode="soft" ) for i in coeff[1:])
10    reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" )
11    return reconstructed_signal
12
13fig, ax = plt.subplots(figsize=(12,8))
14ax.plot(signal, color="b", alpha=0.5, label='original signal')
15rec = lowpassfilter(signal, 0.4)
16ax.plot(rec, 'k', label='DWT smoothing}', linewidth=2)
17ax.legend()
18ax.set_title('Removing High Frequency Noise with DWT', fontsize=18)
19ax.set_ylabel('Signal Amplitude', fontsize=16)
20ax.set_xlabel('Sample No', fontsize=16)
21plt.show()

تصویر زیر در خروجی ایجاد می‌شود. در این تصویر سیگنال با مولفه‌های فرکانس بالا و سیگنال صاف‌شده آن پس از اعمال تبدیل موجک گسسته را می‌توان مشاهده کرد.

همان طور که در تصویر بالا نیز مشاهده می‌شود، می‌توان از طریق تجزیه یک سیگنال و برابر صفر قرار دادن برخی از ضرایب در آن و سپس بازسازی مجدد سیگنال، نویزهای فرکانس بالا در سیگنال را حذف کرد. البته اگر با تکنیک‌های مختلف پردازش سیگنال آشنا باشیم، می‌دانیم که روش‌های مختلفی برای حذف نویز از یک سیگنال وجود دارد.

به عنوان مثال، در پایتون کتابخانه Scipy دارای فیلترهای صاف‌کننده متنوعی است که استفاده از این فیلترها بسیار ساده‌تر است. یکی از فیلترهای صاف‌کننده، فیلتر Savitzky-Golay نام دارد. یکی دیگر از روش‌های حذف نویز، میانگین‌گیری از سیگنال در طول محور زمان است.

سوالی که پیش می‌آید این است که چرا باید از روش تبدیل موجک گسسته که نسبتا پیچیده‌تر است، به جای این روش‌ها استفاده کرد؟ در جواب باید گفت، مزیت اصلی تبدیل موجک گسسته از این ویژگی ناشی می‌شود که اشکال متنوعی از موجک وجود دارند که می‌توان از آن‌ها استفاده کرد. می‌توان یک موجک را انتخاب کرد که شکل آن متناظر با مشخصه‌هایی از پدیده باشد که انتظار مشاهده آن را داریم. به این طریق، تعداد کمتری از مشخصه‌های پدیده که مورد نیاز هستند، در اثر صاف شدن از بین می‌روند.

استفاده از تبدیل موجک گسسته برای طبقه‌بندی سیگنال

در ادامه قصد داریم تا ببینیم چگونه می‌توان از تبدیل موجک گسسته و شبکه عصبی کانولوشنی برای طبقه‌بندی سیگنال‌ها استفاده کرد.

فیلم آموزش شبکه های مخابراتی (رایگان) در فرادرس

کلیک کنید

ایده پنهان در طبقه‌بندی سیگنال با استفاده از تبدیل موجک گسسته

ایده‌ای که در پس طبقه‌بندی سیگنال با استفاده از تبدیل موجک گسسته وجود دارد را می‌توان به صورت زیر بیان کرد:

ابتدا از تبدیل موجک گسسته برای تفکیک یک سیگنال به زیرباندهای فرکانسی مختلف استفاده می‌کنیم. این کار را تا حد ممکن یا تا حد لازم تکرار می‌کنیم. چون انواع مختلف سیگنال‌ها، مشخصه‌های فرکانسی مختلفی را از خود نشان می‌دهند، در نتیجه این تمایز در رفتار باید در یکی از زیرباندهای فرکانسی خود را نشان دهد. بنابراین اگر ویژگی‌ها (Features) را از هریک از زیرباندهای مختلف ایجاد کنیم و از مجموعه تمام ویژگی‌ها به عنوان ورودی در یک طبقه‌بند (Classifier) مانند جنگل تصادفی، ارتقای گرادیان و یا رگرسیون منطقی استفاده کنیم و الگوریتم طبقه‌بندی را با استفاده از این ویژگی‌ها آموزش دهیم، آن‌گاه الگوریتم قادر خواهد بود که تمایز بین سیگنال‌های مختلف را تشخیص دهد و طبقه‌بندی را بر اساس آن انجام دهد. این مفهوم در تصویر زیر به خوبی نشان داده شده است.

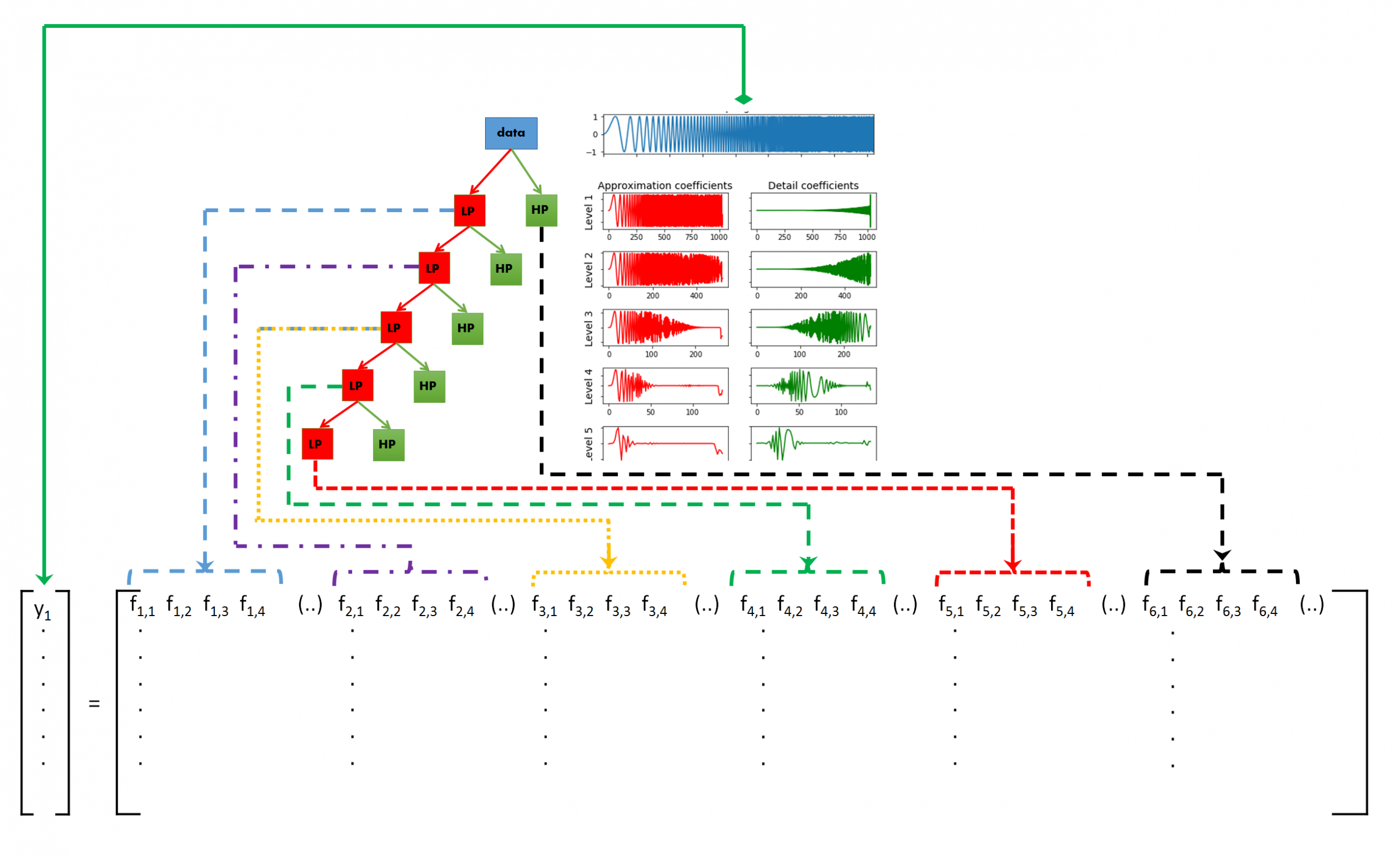
تولید ویژگی از هر زیر باند

حال می‌خواهیم بدانیم از مجموعه مقادیر هر زیر باند چه ویژگی‌هایی را می‌توان ایجاد کرد؟ واضح است که این امر تا حد بسیار زیادی به نوع سیگنال و کاربرد مورد نظر بستگی دارد. اما در حالت کلی، ویژگی‌های زیر را می‌توان به عنوان متداول‌ترین و پر تکرارترین ویژگی‌های مورد استفاده در سیگنال‌ها بیان کرد:

• مقادیر ضرایب مدل اتورگرسیو (Auto-regressive)
• مقادیر آنتروپی (Entropy). این مقادیر را می‌توان به عنوان معیاری از پیچیدگی (Complexity) سیگنال در نظر گرفت.

و یا ویژگی‌های آماری مانند:

• واریانس
• انحراف معیار
• میانگین، میانه
• مقدار صدک 25ام
• مقدار صدک 75ام
• مقدار مجذور میانگین مربعات
• میانگین مشتقات
• نرخ عبور از صفر. (تعداد دفعات عبور سیگنال از $$y=0$$)
• نرخ عبور از میانگین. (تعداد دفعات عبور سیگنال از $$\text{y} = \text{mean} (\text{y})$$)

البته ایده دیگری نیز برای ایجاد ویژگی از زیرباندهای سیگنال وجود دارد. می‌توانید از تعدادی از ویژگی‌هایی که در اینجا توصیف شدند استفاده کنید و یا حتی می توانید تمامی آن‌ها را با هم به کار برید. اکثر طبقه‌بندها یا کلاسیفایرها در پکیج Scikit-Learn آنقدر توانمند هستند که می‌توانند تعداد زیادی ویژگی ورودی را مدیریت کنند و انواع مفید و غیر مفید ویژگی‌ها را از یکدیگر تمایز دهند. البته توجه کنید که تعداد بسیار زیادی توابع آماری در کتابخانه scipy.stats.‎ وجود دارند که می‌توان با استفاده از آن‌ها ویژگی‌های بیشتری را نیز ایجاد کرد.

فیلم آموزش مقدماتی پردازش سیگنال با پایتون Python در فرادرس

کلیک کنید

با استفاده از قطعه کد زیر می‌توان نحوه استفاده از تعدادی از ویژگی‌های بیان شده در بالا را مشاهده کرد.

1def calculate_entropy(list_values):
2    counter_values = Counter(list_values).most_common()
3    probabilities = [elem[1]/len(list_values) for elem in counter_values]
4    entropy=scipy.stats.entropy(probabilities)
5    return entropy
6
7def calculate_statistics(list_values):
8    n5 = np.nanpercentile(list_values, 5)
9    n25 = np.nanpercentile(list_values, 25)
10    n75 = np.nanpercentile(list_values, 75)
11    n95 = np.nanpercentile(list_values, 95)
12    median = np.nanpercentile(list_values, 50)
13    mean = np.nanmean(list_values)
14    std = np.nanstd(list_values)
15    var = np.nanvar(list_values)
16    rms = np.nanmean(np.sqrt(list_values**2))
17    return [n5, n25, n75, n95, median, mean, std, var, rms]
18
19def calculate_crossings(list_values):
20    zero_crossing_indices = np.nonzero(np.diff(np.array(list_values) > 0))[0]
21    no_zero_crossings = len(zero_crossing_indices)
22    mean_crossing_indices = np.nonzero(np.diff(np.array(list_values) > np.nanmean(list_values)))[0]
23    no_mean_crossings = len(mean_crossing_indices)
24    return [no_zero_crossings, no_mean_crossings]
25
26def get_features(list_values):
27    entropy = calculate_entropy(list_values)
28    crossings = calculate_crossings(list_values)
29    statistics = calculate_statistics(list_values)
30    return [entropy] + crossings + statistics

در قطعه کد بالا توابع زیر مورد استفاده قرار گرفته‌اند:

• یک تابع برای محاسبه مقدار آنتروپی مربوط به سیگنال ورودی.
• یک تابع برای محاسبه چند مشخصه آماری مانند: میانگین، چند صدک، انحراف معیار و واریانس و ....
• یک تابع برای محاسبه نرخ عبور از صفر و نرخ عبور از میانگین.
• یک تابع برای ترکیب نتایج سه تابع بالا.

تابع نهایی در برنامه بالا ۱۲ ویژگی متمایز را برای هر لیست از مقادیر در خروجی باز می‌گرداند. بنابراین اگر یک سیگنال به ۱۰ زیر باند متمایز تجزیه شود و برای هر زیر باند ویژگی‌هایی تولید کنیم، در نهایت 120 ویژگی برای هر سیگنال خواهیم داشت.

استفاده از ویژگی‌ها و کتابخانه Scikit-Learn برای طبقه‌بندی دو دیتاست ECG

تا این قسمت مطالب بسیاری را بیان کردیم. در گام بعد، باید سیگنال‌های مجموعه آموزش را با استفاده از تبدیل موجک گسسته به زیر باندهای خود تجزیه کنیم و برای هر زیر باند ویژگی‌ها را محاسبه کنیم. سپس از ویژگی‌ها برای آموزش یک طبقه‌بند استفاده کنیم تا طبقه‌بند بتواند سیگنال‌های مجموعه تست را پیش‌بینی کند. این فرایند را برای دو دیتاست سری زمانی انجام می‌دهیم.

1. اولین دیتاست UCI-HAR است که در بخش‌های قبل از آن استفاده کردیم. این دیتاست شامل داده‌های ضبط شده سنسورهای گوشی‌های هوشمند از فعالیت‌های مختلف انسان مانند نشستن، ایستادن، راه رفتن، بالا رفتن از پله و پایین رفتن از پله است.
2. دومین دیتاست، PhysioNet نام دارد که شامل داده‌های ECG است.دیتاست PhysioNet را می‌توانید با کلیک روی لینک دانلود کنید. دیتاست PhysioNet شامل مجموعه‌ای از سیگنال‌های ECG اندازه‌گیری شده از افراد سالم (NSR) و افراد با بیماری ARR یا CHF است. در مجموع دیتاست از 96 اندازه‌گیری ARR و 36 اندازه‌گیری NSR و 30 اندازه‌گیری CHF تشکیل شده است.

بعد از این‌که هر دو دیتاست را دانلود کردیم و آن‌ها را در پوشه صحیح قرار دادیم، گام بعدی این است که آن‌ها را در حافظه بارگذاری کنیم. در بخش قبل با نحوه بارگذاری دیتاست UCI-HAR آشنا شدیم. در قطعه کد زیر نحوه بارگذاری دیتاست ECG را مشاهده می‌کنید.

1def load_ecg_data(filename):
2    raw_data = sio.loadmat(filename)
3    list_signals = raw_data['ECGData'][0][0][0]
4    list_labels = list(map(lambda x: x[0][0], raw_data['ECGData'][0][0][1]))
5    return list_signals, list_labels
6
7
8##########
9
10filename = './data/ECG_data/ECGData.mat'
11data_ecg, labels_ecg = load_ecg_data(filename)
12training_size = int(0.6*len(labels_ecg))
13train_data_ecg = data_ecg[:training_size]
14test_data_ecg = data_ecg[training_size:]
15train_labels_ecg = labels_ecg[:training_size]
16test_labels_ecg = labels_ecg[training_size:]

توجه کنید که دیتاست ECG به صورت یک فایل MATLAB ذخیره شده است. بنابراین باید از scipy.io.loadmat()‎ استفاده کنیم تا این فایل در پایتون باز شود و داده‌های اندازه‌گیری و برچسب هر کدام در دو لیست جداگانه بازیابی شود.

توجه کنید که دیتاست UCI HAR در فایل‌هایی با پسوند txt. ذخیره شده است و بعد از خواندن داده‌ها، باید آن‌ها را در یک آرایه numpy با سایز $$(\text {no of signals, length of signal, no of components}) = (10299 , 128, 9)$$ ذخیره کنیم. حال می‌خواهیم ببینیم ویژگی‌های سیگنال‌ها به چه صورت از دیتاست‌ها استخراج می‌شوند.

فیلم آموزش مقدماتی پردازش سیگنال با پایتون Python در فرادرس

کلیک کنید

برای این کار باید قطعه کد زیر را در پایتون اجرا کنیم.

1def get_uci_har_features(dataset, labels, waveletname):
2    uci_har_features = []
3    for signal_no in range(0, len(dataset)):
4        features = []
5        for signal_comp in range(0,dataset.shape[2]):
6            signal = dataset[signal_no, :, signal_comp]
7            list_coeff = pywt.wavedec(signal, waveletname)
8            for coeff in list_coeff:
9                features += get_features(coeff)
10        uci_har_features.append(features)
11    X = np.array(uci_har_features)
12    Y = np.array(labels)
13    return X, Y
14
15def get_ecg_features(ecg_data, ecg_labels, waveletname):
16    list_features = []
17    list_unique_labels = list(set(ecg_labels))
18    list_labels = [list_unique_labels.index(elem) for elem in ecg_labels]
19    for signal in ecg_data:
20        list_coeff = pywt.wavedec(signal, waveletname)
21        features = []
22        for coeff in list_coeff:
23            features += get_features(coeff)
24        list_features.append(features)
25    return list_features, list_labels
26
27X_train_ecg, Y_train_ecg = get_ecg_features(train_data_ecg, train_labels_ecg, 'db4')
28X_test_ecg, Y_test_ecg = get_ecg_features(test_data_ecg, test_labels_ecg, 'db4')
29
30X_train_ucihar, Y_train_ucihar = get_uci_har_features(train_signals_ucihar, train_labels_ucihar, 'rbio3.1')
31X_test_ucihar, Y_test_ucihar = get_uci_har_features(test_signals_ucihar, test_labels_ucihar, 'rbio3.1')

کاری که در کد بالا انجام دادیم این است که توابعی برای تولید ویژگی از سیگنال‌های ECG و UCI HAR نوشتیم. در واقع این دو تابع تفاوتی با یکدیگر ندارند و تنها دلیل اینکه از دو تابع مختلف برای این دو دیتاست استفاده کردیم این است که داده‌ها در هر کدام از آن ها با یک فرمت مختلف ذخیره شده است. داده‌ها در دیتاست ECG در قالب لیست ذخیره شده‌اند، در حالی که داده‌ها در دیتاست UCI HAR در قالب یک numpy ndarray سه بعدی ذخیره شده‌اند.

در برنامه فوق برای داده‌های دیتاست ECG، روی لیست سیگنال‌ها حلقه زده‌ایم و روی هر سیگنال تبدیل موجک گسسته را اعمال کرده‌ایم که در نهایت لیستی از ضرایب را باز می‌گرداند. برای هر یک از این سیگنال‌ها یا به عبارت دیگر برای هر یک از این زیر باندها، ویژگی‌ها را با استفاده از تابعی که در بخش قبل تعریف کردیم، استخراج می‌کنیم. ویژگی‌هایی که با استفاده از تمام ضرایب مختلف مربوط به یک سیگنال محاسبه شده‌اند، به یکدیگر الحاق می‌شوند؛ زیرا این ویژگی‌ها در واقع متعلق به یک سیگنال هستند.

همین کار را با داده‌های دیتاست UCI HAR نیز انجام می‌دهیم. تنها تفاوت در این است که این بار دو حلقه for داریم؛ زیرا هر سیگنال از ۹ مولفه تشکیل شده است. ویژگی‌هایی که از هر یک از زیر باندهای هر مولفه یک سیگنال تولید می‌شود، به یکدیگر الحاق می‌شوند.

حال که ویژگی‌ها را برای هر دیتاست محاسبه کرده‌ایم، می‌توانیم از تابع دسته‌بند یا طبقه‌بند ارتقای گرادیان (GradientBoostingClassifier) در کتابخانه scikit-learn استفاده کنیم و آن را آموزش دهیم. برای این کار باید قطعه کد زیر را در پایتون اجرا کنیم.

1cls = GradientBoostingClassifier(n_estimators=2000)
2cls.fit(X_train_ecg, Y_train_ecg)
3train_score = cls.score(X_train_ecg, Y_train_ecg)
4test_score = cls.score(X_test_ecg, Y_test_ecg)
5print("Train Score for the ECG dataset is about: {}".format(train_score))
6print("Test Score for the ECG dataset is about: {.2f}".format(test_score))
7
8### 
9
10cls = GradientBoostingClassifier(n_estimators=2000)
11cls.fit(X_train_ucihar, Y_train_ucihar)
12train_score = cls.score(X_train_ucihar, Y_train_ucihar)
13test_score = cls.score(X_test_ucihar, Y_test_ucihar)
14print("Train Score for the UCI-HAR dataset is about: {}".format(train_score))
15print("Test Score for the UCI-HAR dataset is about: {.2f}".format(test_score))
16
17*** Train Score for the ECG dataset is about: 1.0
18*** Test Score for the ECG dataset is about: 0.93
19*** Train Score for the UCI_HAR dataset is about: 1.0
20*** Test Score for the UCI-HAR dataset is about: 0.95

همان طور که می‌بینید، نتایج هنگام استفاده از تبدیل موجک گسسته به همراه Gradient Boosting Classifier بسیار عالی است. این روش روی دیتاست ECG دارای دقت 93 درصد و روی دیتاست UCI-HAR دارای دقت ۹۵ درصد است.

مقایسه دقت طبقه‌بندی با استفاده از تبدیل موجک گسسته، تبدیل فوریه و شبکه عصبی بازگشتی (RNN)

اگر طبقه‌بندی داده‌های دیتاست UCI-HAR را با استفاده از تبدیل فوریه انجام دهیم، آن‌گاه دقت بر روی داده‌های تست برابر با ۹۱ درصد خواهد بود. از طرف دیگر، اگر طبقه‌بندی را با استفاده از شبکه عصبی بازگشتی انجام دهیم، آن‌گاه بالاترین دقت روی داده‌های تست حدودا ۸۶ درصد به دست می‌آید. در حالی که با استفاده از تبدیل موجک و CNN توانستیم به دقت ۹۴ درصد و با استفاده از تبدیل موجک و ارتقای گرادیان به دقت ۹۵ درصد روی داده‌های تست برسیم.

واضح است که استفاده از تبدیل موجک باعث شده که دقت طبقه‌بندی نسبت به سایر روش‌ها بسیار بالاتر باشد. این کار را می‌توان با دیتاست‌های دیگر نیز انجام داد و به احتمال زیاد باز هم نتایج با استفاده از تبدیل موجک نسبت به سایر روش‌ها بهتر خواهد بود. نکته دیگری که در اینجا لازم است به آن توجه کنیم این است که شبکه عصبی بازگشتی بدترین نتیجه را در بین این سه روش دارد. حتی استفاده از روش بسیار ساده‌ای مانند تبدیل فوریه و یافتن محل پیک‌های طیف فرکانسی، به نتیجه بهتری نسبت به استفاده از شبکه عصبی بازگشتی می‌توان دست یافت.

این نکته بسیار جالب است، زیرا یکی از ویژگی‌های شبکه عصبی بازگشتی، توانایی یادگیری وابستگی‌های موقتی (Temporal Dependencies) در داده‌های ترتیبی (Sequential Data) است. اگر تبدیل فوریه قادر است هر سیگنالی را بدون توجه به پیچیدگی آن توسط المان‌های فوریه توصیف کند، آن‌گاه با توجه به وابستگی‌های موقتی، چه چیز‌های بیشتری را می‌تواند یاد بگیرد.

دقت به دست آمده با استفاده از تبدیل موجک گسسته به ویژگی‌هایی که برای محاسبه در نظر گرفته می‌شود، موجک انتخاب شده و نوع الگوریتم دسته‌بند نیز بستگی دارد. برای یافتن درک نسبی، در تصویر زیر دقت طبقه‌بندی داده‌های تست روی دیتاست‌های UCI-HAR و ECG به ازای تمام موجک‌های PyWavelets و ۵ مورد از پرکاربردترین الگوریتم‌های طبقه‌بندی کتابخانه scikit-learn نشان داده شده است.

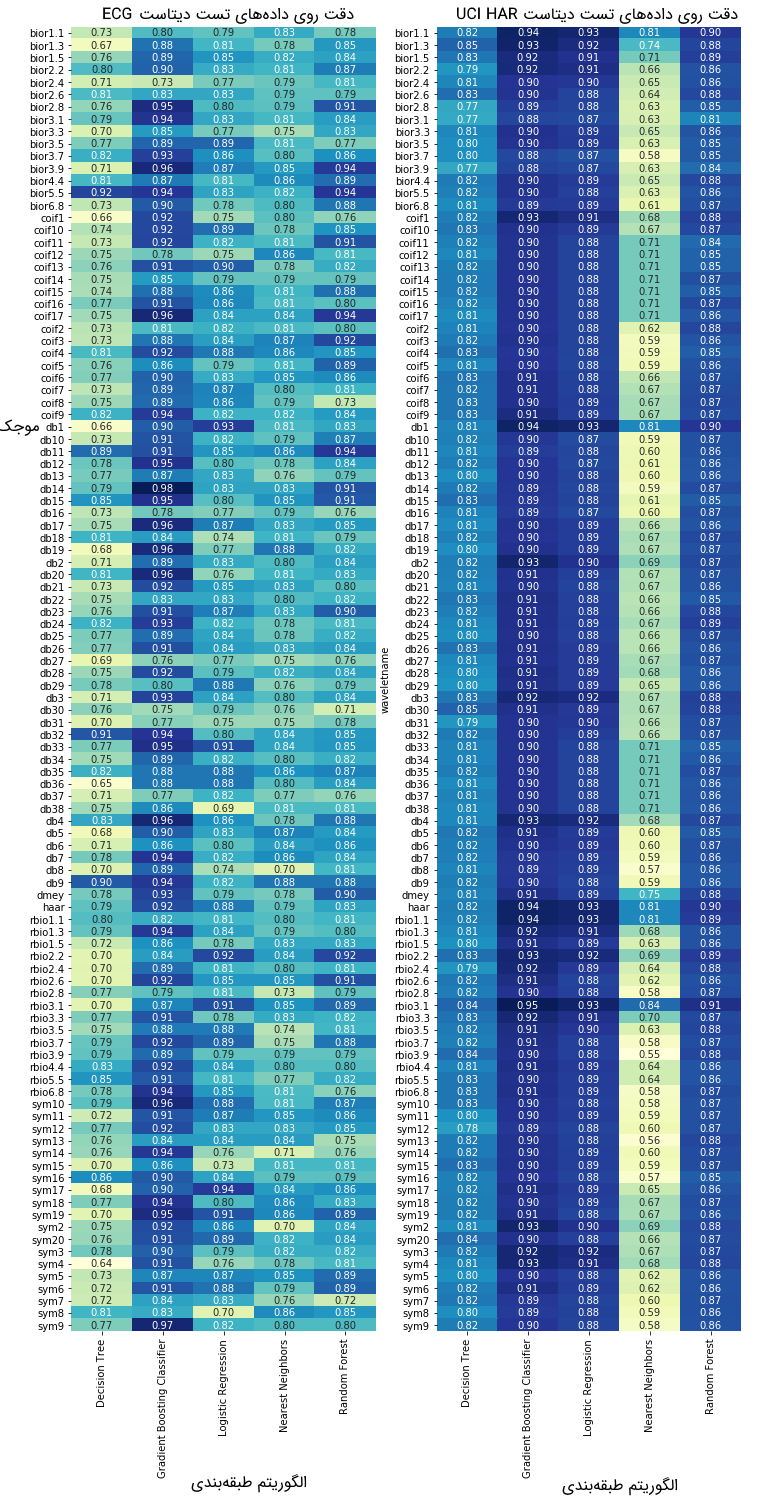
با توجه به این تصویر می‌توان دید که دقت طبقه‌بندی، متناظر با الگوریتم طبقه‌بندی انتخاب شده و تابع موجک، تغییر خواهد کرد، اما در حالت کلی می‌توان گفت که الگوریتم ارتقای گرادیان عملکرد بهتری دارد. نکته دیگری که باید به آن اشاره کرد این است که موجک انتخاب شده می‌تواند تاثیر زیادی روی دقت نهایی طبقه‌بندی داشته باشد. بهترین راه برای انتخاب موجک مناسب، آزمایش و خطای بسیار و نیز انجام تحقیق روی کاربرد قبل از پیاده‌سازی است.

تبدیل موجک در متلب

برای آشنایی با پیاده‌سازی تبدیل موجک در متلب در این قسمت می‌خواهیم تبدیل موجک را روی بخشی از دیتاست ال نینو اعمال کنیم. داده‌ها را می‌توان از طریق کلیک روی sst_nino3.dat دانلود کرد. این فایل شامل داده‌های دیتاست ال نینو است که باید در قالب فایل dat. در متلب ذخیره شود. حال باید توابع chisquare_inv.m و chisquare_solve.m و wave_bases.m و wave_signif.m و wavelet.m را دانلود کرده و در یک محل قرار دهیم.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

در نهایت برای تست کردن نتیجه اعمال تبدیل موجک می‌توان کد زیر را اجرا کرد.

wavetest.m

1%WAVETEST Example Matlab script for WAVELET, using NINO3 SST dataset
2%
3% See "http://paos.colorado.edu/research/wavelets/"
4% Written January 1998 by C. Torrence
5%
6% Modified Oct 1999, changed Global Wavelet Spectrum (GWS) to be sideways,
7%   changed all "log" to "log2", changed logarithmic axis on GWS to
8%   a normal axis.
9
10load 'sst_nino3.dat'   % input SST time series
11sst = sst_nino3;
12
13%------------------------------------------------------ Computation
14
15% normalize by standard deviation (not necessary, but makes it easier
16% to compare with plot on Interactive Wavelet page, at
17% "http://paos.colorado.edu/research/wavelets/plot/"
18variance = std(sst)^2;
19sst = (sst - mean(sst))/sqrt(variance) ;
20
21n = length(sst);
22dt = 0.25 ;
23time = [0:length(sst)-1]*dt + 1871.0 ;  % construct time array
24xlim = [1870,2000];  % plotting range
25pad = 1;      % pad the time series with zeroes (recommended)
26dj = 0.25;    % this will do 4 sub-octaves per octave
27s0 = 2*dt;    % this says start at a scale of 6 months
28j1 = 7/dj;    % this says do 7 powers-of-two with dj sub-octaves each
29lag1 = 0.72;  % lag-1 autocorrelation for red noise background
30mother = 'Morlet';
31
32% Wavelet transform:
33[wave,period,scale,coi] = wavelet(sst,dt,pad,dj,s0,j1,mother);
34power = (abs(wave)).^2 ;        % compute wavelet power spectrum
35
36% Significance levels: (variance=1 for the normalized SST)
37[signif,fft_theor] = wave_signif(1.0,dt,scale,0,lag1,-1,-1,mother);
38sig95 = (signif')*(ones(1,n));  % expand signif --> (J+1)x(N) array
39sig95 = power ./ sig95;         % where ratio > 1, power is significant
40
41% Global wavelet spectrum & significance levels:
42global_ws = variance*(sum(power')/n);   % time-average over all times
43dof = n - scale;  % the -scale corrects for padding at edges
44global_signif = wave_signif(variance,dt,scale,1,lag1,-1,dof,mother);
45
46% Scale-average between El Nino periods of 2--8 years
47avg = find((scale >= 2) & (scale < 8));
48Cdelta = 0.776;   % this is for the MORLET wavelet
49scale_avg = (scale')*(ones(1,n));  % expand scale --> (J+1)x(N) array
50scale_avg = power ./ scale_avg;   % [Eqn(24)]
51scale_avg = variance*dj*dt/Cdelta*sum(scale_avg(avg,:));   % [Eqn(24)]
52scaleavg_signif = wave_signif(variance,dt,scale,2,lag1,-1,[2,7.9],mother);
53
54whos
55
56%------------------------------------------------------ Plotting
57
58%--- Plot time series
59subplot('position',[0.1 0.75 0.65 0.2])
60plot(time,sst)
61set(gca,'XLim',xlim(:))
62xlabel('Time (year)')
63ylabel('NINO3 SST (degC)')
64title('a) NINO3 Sea Surface Temperature (seasonal)')
65hold off
66
67%--- Contour plot wavelet power spectrum
68subplot('position',[0.1 0.37 0.65 0.28])
69levels = [0.0625,0.125,0.25,0.5,1,2,4,8,16] ;
70Yticks = 2.^(fix(log2(min(period))):fix(log2(max(period))));
71contour(time,log2(period),log2(power),log2(levels));  %*** or use 'contourfill'
72%imagesc(time,log2(period),log2(power));  %*** uncomment for 'image' plot
73xlabel('Time (year)')
74ylabel('Period (years)')
75title('b) NINO3 SST Wavelet Power Spectrum')
76set(gca,'XLim',xlim(:))
77set(gca,'YLim',log2([min(period),max(period)]), ...
78	'YDir','reverse', ...
79	'YTick',log2(Yticks(:)), ...
80	'YTickLabel',Yticks)
81% 95% significance contour, levels at -99 (fake) and 1 (95% signif)
82hold on
83contour(time,log2(period),sig95,[-99,1],'k');
84hold on
85% cone-of-influence, anything "below" is dubious
86plot(time,log2(coi),'k')
87hold off
88
89%--- Plot global wavelet spectrum
90subplot('position',[0.77 0.37 0.2 0.28])
91plot(global_ws,log2(period))
92hold on
93plot(global_signif,log2(period),'--')
94hold off
95xlabel('Power (degC^2)')
96title('c) Global Wavelet Spectrum')
97set(gca,'YLim',log2([min(period),max(period)]), ...
98	'YDir','reverse', ...
99	'YTick',log2(Yticks(:)), ...
100	'YTickLabel','')
101set(gca,'XLim',[0,1.25*max(global_ws)])
102
103%--- Plot 2--8 yr scale-average time series
104subplot('position',[0.1 0.07 0.65 0.2])
105plot(time,scale_avg)
106set(gca,'XLim',xlim(:))
107xlabel('Time (year)')
108ylabel('Avg variance (degC^2)')
109title('d) 2-8 yr Scale-average Time Series')
110hold on
111plot(xlim,scaleavg_signif+[0,0],'--')
112hold off
113
114% end of code

نتیجه حاصل از اجرای کد بالا، در تصویر زیر نشان داده شده است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پردازش سیگنال
• آموزش مقدماتی پردازش سیگنال با Python (پایتون)
• مجموعه آموزش‌‌های هوش مصنوعی
• آموزش یادگیری عمیق (Deep learning)
• تبدیل فوریه سریع (fft) — به زبان ساده
• سری فوریه مختلط — به زبان ساده
• شبکه عصبی در متلب — از صفر تا صد

^^