سری زمانی در علم داده — از صفر تا صد

مبحث «سری‌های زمانی» (Time Series) به داده‌های وابسته به زمان مربوط می‌شود. تحلیل سری زمانی نیز یک از روش‌های تحلیل چنین داده‌هایی است. برای مثال تشخیص روند تغییرات ارزش سهام با توجه به داده‌های جمع‌آوری شده در طول یک سال می‌تواند تحلیل سری زمانی نامیده شود.

معمولا در تحلیل سری زمانی، هدف ایجاد مدلی است که رفتار داده‌های مرتبط با زمان را تشخیص دهد. به این ترتیب می‌توان عمل پیش‌بینی را برای آینده صورت داد. به نظر می‌رسد تحلیل سری زمانی، کمک می‌کند که با مطالعه گذشته و درس گرفتن از آن، آینده را پیش‌بینی کرد و به بهتر شدن آن دست زد.

برای آشنایی با مفاهیم اولیه و آماری این مبحث می‌توانید به نوشتار تحلیل سری زمانی — تعریف و مفاهیم اولیه مراجعه کنید. همچنین برای آشنایی با ابزارهای تحلیل سری زمانی بهتر است نوشتار فرادرس در این زمینه با نام تابع خودهمبستگی (Autocorrelation Function) — مفاهیم و کاربردها را نیز مطالعه کنید.

سری زمانی در علم داده

گاهی می‌توان سری زمانی را به صورت یک مسئله رگرسیون با متغیر مستقل «زمان» در نظر گرفت. در این حالت هدف از انجام تحلیل سری زمان، محاسبه مقدار متغیر وابسته در زمان آینده است. در ادامه با اصطلاحاتی نظیر «میانگین متحرک» (Moving Average)، «هموار‌سازی نمایی» (Exponential Smoothing)، «ایستایی» (Stationary)، «خودهمبستگی» (Autocorrelation) و مدل SARIMA آشنا خواهیم شد.

فیلم آموزش تحلیل سری های زمانی با پایتون و آر R در فرادرس

کلیک کنید

تابع خود همبستگی (Autocorrelation Function)

می‌توان خود همبستگی را به صورت شباهت بین مشاهدات در نظر گرفت. تابع خود همبستگی نیز به منظور اندازه‌گیری این شباهت تهیه شده است. در تصویر زیر نمونه‌ای از نمودار تابع خودهمبستگی را مشاهده می‌کنید.

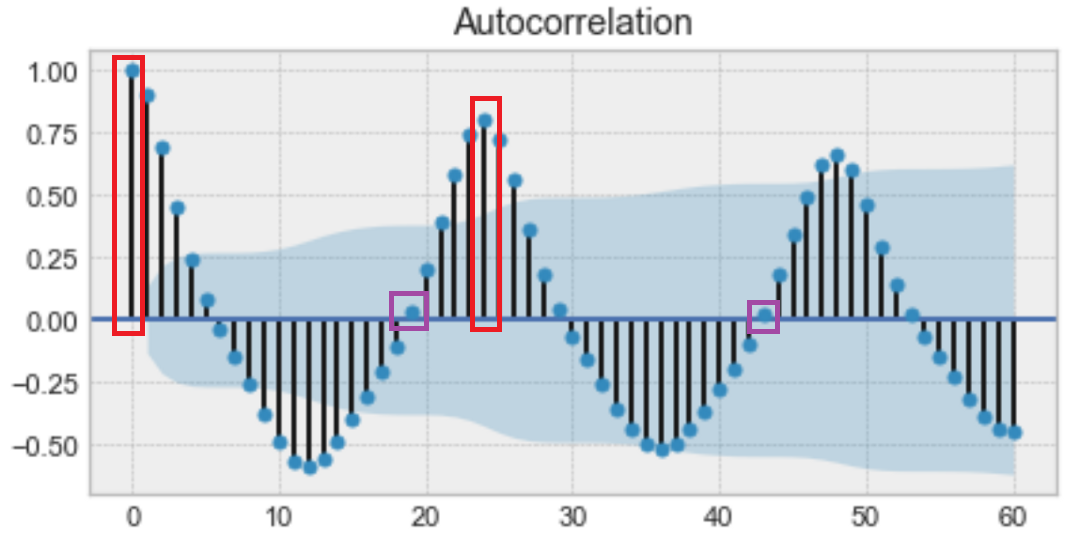
اگر با دقت به این نمودار نگاه کنید، متوجه می‌شوید که مقدارهای مربوط به زمان اول و زمان ۲۴، شباهت زیادی با یکدیگر دارند. همچنین مشاهده مربوط به زمان ۱۹ با زمان ۴۳ نیز مشابهت زیادی دارند. این شباهت‌ها را در نقاط دیگر مانند ۱۲ امین و ۳۵ امین نقاط نیز می‌توان مشاهده کرد. به این ترتیب می‌توان نتیجه گرفت که در هر ۲۴ واحد زمانی، پدیده زمانی یا مقدارهایشان تکرار یا مشابه یکدیگر تولید می‌شوند. به همین علت این نمودار به صورت تناوبی و به شکل تابع سینوس (Sin) ترسیم شده است. این نمودار می‌تواند بیانگر وجود «تغییرات فصلی» (Seasonality) یا تناوبی در سری زمانی باشد. به این ترتیب با توجه به وجود تغییرات فصلی، اگر بتوانیم مقدار مربوط به این سری یا دنباله را در زمان t بدست آوریم، مقدار پیش‌بینی را برای زمان t+24 نیز خواهیم داشت.

تغییرات فصلی (Seasonality)

منظور از تغییرات فصلی، وجود نوساناتی است که به صورت تناوبی در سری زمانی وجود دارد. برای مثال میزان مصرف الکتریسیته، دارای تغییرات فصلی است، البته در اینجا شاید تغییرات تناوبی با طول دوره فصل‌های سال نباشد و در هر دوره ۲۴ ساعتی تکرار شوند. مشخص است که میزان مصرف برق در روز افزایشی بوده ولی در طول شب کاهشی است. در این جا دوره تناوب به صورت ۲۴ ساعتی است. همین امر را می‌توان در میزان فروش در عیدها نسبت به روزهای دیگر سال در نظر گرفت. در اینجا دوره تناوب یا تغییرات فصلی در یک سال صورت می‌گیرد.

نمودار زیر مربوط به تغییرات میزان مصرف برق در تاریخ‌های مختلف است. مشخص است که در ابتدا (نیمه شب) مصرف، حداقل ممکن است و به تناوب این مقدار مشاهده می‌شود. در طول روز نیز میزان مصرف افزایشی شده و باز هم به صورت تناوبی در روزهای دیگر نیز تکرار می‌شود.

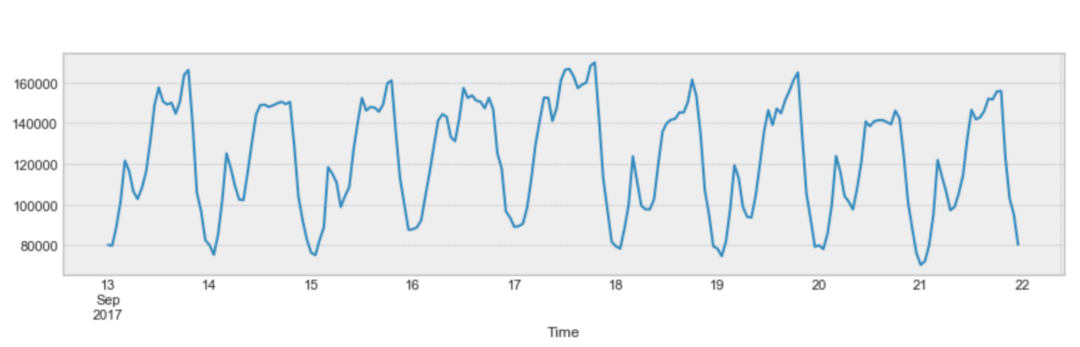
توجه داشته باشید که تشخیص تغییرات فصلی به کمک رسم نمودار و یا تابع خودهمبستگی نیز امکان‌پذیر است. بنابراین اگر در نمودار خودهمبستگی تغییرات به صورت سینوسی دیده شود می‌توان رای به وجود تغییرات فصلی در سری زمانی داد.

ایستایی (Stationary)

یکی از خصوصیات اصلی و مهم در سری زمان، ایستایی است. سری زمانی که خاصیت ایستایی داشته باشد را می‌توان تجزیه و تحلیل کرد. بسیاری از تبدیلات مانند میانگین متحرک (Moving Average)، در سری زمانی به منظور ایستا کردن آن به کار می‌روند.

سری زمانی را ایستا گویند اگر خصوصیات آماری آن مانند میانگین و واریانس در طول زمان ثابت باشد. از طرفی ماتریس کوواریانس برای سری زمانی باید مستقل از زمان باشد. با توجه به نمودار قبلی می‌توان ثابت بودن میانگین و واریانس را مشاهده کرد. زیرا به نظر می‌رسد در طی هر روز میانگین مصرف انرژی برق یکسان است. از طرفی تغییرات مصرف نیز حول میانگین ثابت به نظر می‌رسد. ولی معمولا، ارزش سهام در بازار بورس، یک پدیده ایستا نیست زیرا می‌توان روند افزایشی یا کاهشی را به خوبی در آن مشاهده کرد. همچنین تغییرات نسبت به میانگین هر روز می‌تواند متفاوت باشد.

در تحلیل سری زمانی، قبل از مدل‌سازی، باید سری را به صورت ایستا درآورد. به این منظور روش‌های بررسی ایستایی سری زمانی در ادامه مورد بررسی قرار می‌گیرند.

بررسی ایستایی سری زمانی

یکی از روش‌های بررسی ایستایی، انجام آزمون Dickey-Fuller است. به کمک این آزمون آماری می‌توان ایستایی یک سری زمانی را مورد بررسی قرار داد. اگر به زبان آزمون فرض آماری در مورد این آماره صحبت کنیم، می‌توان گفت که فرض صفر در این آزمون ناایستا بودن سری زمانی است. در نتیجه اگر با توجه به مقدار p-Value یا همان مقدار احتمال، فرض صفر رد شود، رای به ایستا بودن سری زمانی خواهیم داد.

با توجه به مقدار احتمال (p) می‌توان در مورد ایستایی سری زمانی تصمیم گرفت. اگر p کوچکتر از احتمال خطای نوع اول ($$\alpha$$) باشد، فرض صفر رد شده و رای به ایستایی سری زمانی خواهیم داد. در غیر اینصورت دلیلی برای وجود ایستایی سری زمانی وجود ندارد. اطلاع دارید که معمولا مقدار $$\alpha$$ را برابر با 0.05‌ یا 5% در نظر می‌گیرند.

به تصویر زیر نگاه کنید. با توجه به شکل تغییرات سری زمانی و مقدار احتمال $$p-Value=0.518$$ متوجه می‌شویم که سری زمانی ایستا نیست.

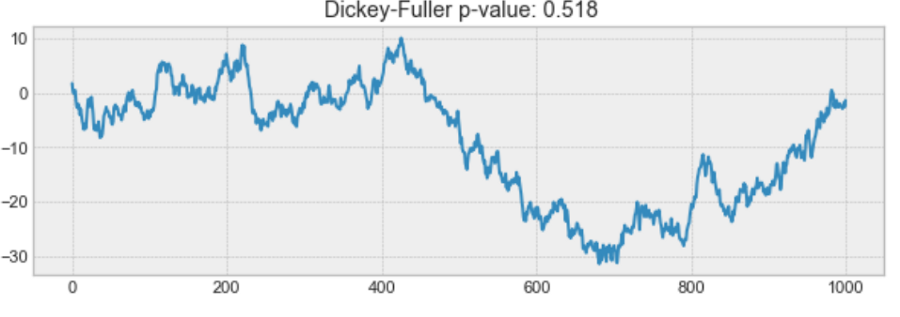
نکته: در اینجا از نحوه محاسبه شاخص Dickey-Fuller صرف نظر کرده‌ایم زیرا در بیشتر نرم‌افزارهای تحلیل سری زمانی محاسبات مربوط به آن قابل انجام است. از طرفی تفسیری که از آن بدست می‌آید مهم است تا بتوان ایستایی سری زمانی را تشخیص داد.

مدل‌سازی سری زمانی

به منظور مدل‌سازی سری زمانی روش‌های مختلفی با توجه به ساختار داده‌های سری، وجود دارد. در اینجا به سه روش عمده اشاره خواهیم کرد.

• میانگین متحرک (Moving Average)
• هموارسازی نمایی (Exponential Smoothing)
• مدل ترکیبی (SARIMA)

مدل میانگین متحرک (Moving Average)

یکی از ساده‌ترین مدل‌های سری زمانی، میانگین متحرک است. در این مدل، مقدار پیش‌بینی برای زمان بعدی به صورت میانگین مقدارهای قبلی خواهد بود. به همین دلیل مدل را به صورت میانگین متحرک نامیده‌اند. اگر مدل، ایستا باشد، در بسیاری از مواقع مدل میانگین متحرک قابل استفاده و البته از دقت مناسبی نیز برخوردار خواهد بود. در غیر اینصورت به کمک میانگین متحرک می‌توان روند یک سری زمانی را تشخیص داد. با تعریف یک «پنجره» (Window) از شیوه میانگین متحرک برای هموارسازی سری زمانی و تغیین نقاط تغییر روند می‌توان استفاده کرد.

فیلم آموزش سری های زمانی فصلی (رایگان) در فرادرس

کلیک کنید

نکته: منظور از پنجره در سری زمانی، بازه‌ای از سری زمانی است که به منظور تحلیل دقیق‌تر رفتار سری به کار گرفته می‌شود.

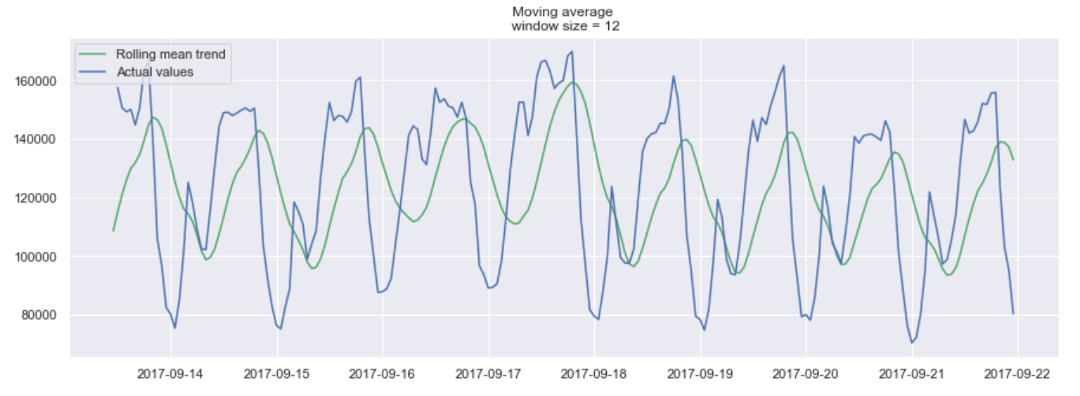
در تصویر زیر با استفاده از تکنیک میانگین متحرک، روند تغییرات میانگین (Rolling mean Trend) نمایش داده شده است. اندازه پنجره در این نمودار برابر با ۲۴ است. به این ترتیب برای بازه‌های ۲۴ ساعتی میانگین محاسبه شده است. برای مثال فاصله میانگین مصرف انرژی در بازه ساعت ۱۵ یک روز تا ساعت ۱۵ روز دیگر ملاک تعیین یک نقطه از خط سبز رنگ شده است. به همین ترتیب در کل یک روز از میانگین‌های مصرف در بازه‌های ۲۴ ساعتی استفاده شده است.

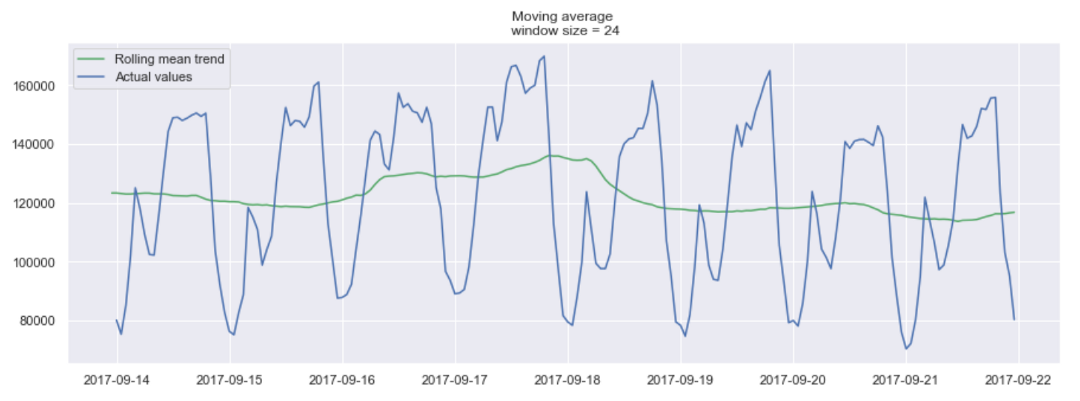
همانطور که دیده می‌شود، خطوط آبی رنگ مقدارهای واقعی و خطوط سبز رنگ میانگین متحرک با پنجره (یا تاخیر - Lag) برابر با ۲۴ را نشان می‌دهند. به نظر می‌رسد تا تاریخ 29-09-2017 روند صعودی و از آن به بعد میانگین میزان مصرف انرژی، نزولی است. از طرفی خط سبز رنگ در نمودار، نمایش هموار شده (Smoothed) سری زمانی با اندازه پنجره ۲۴ است. با تمرکز روی خطوط آبی نمودار که مربوط به سری زمانی است، مشخص است که در هر ۲۴ ساعت دو نقطه به عنوان قله (Peak) مصرف دیده می‌شوند. هر چه اندازه پنجره را کوچکتر انتخاب کنیم، میزان هموار سازی در مدل میانگین متحرک کاهش خواهد یافت. در تصویر زیر با اندازه پنجره ۱۲، تغییرات خط روند که بوسیله میانگین متحرک تولید شده بیشتر از حالت قبل با اندازه پنجره ۲۴ است. به این ترتیب هموارسازی کمتر صورت گرفته و به نظر می‌رسد سری زمانی ایستا نشده است.

هموارسازی نمایی (Exponential Smoothing)

هموارسازی نمایی نیز از همان منطق هموار سازی میانگین متحرک پیروی می‌کند. به این ترتیب می‌توان این روش را به صورت میانگین وزنی برای داده‌های سری زمانی در نظر گرفت که به داده‌های دورتر وزن کمتری در محاسبه میانگین می‌دهد. کاهش وزن مقدارهای گذشته دور در حقیقت از اهمیتشان در محاسبه و پیش‌بینی مقادیر مربوط به آینده می‌کاهد و داده‌های مربوط به حال حاضر تاثیر بیشتری خواهند داشت.

از لحاظ ریاضی، مدل هموارسازی نمایی را می‌توان به صورت زیر نمایش داد:

$$\large y_t=\alpha x_t+(1-\alpha)y_{t-1}, \;\;t>0$$

در اینجا منظور از $$x_t$$ مقدار واقعی سری در زمان t است و $$y_t$$‌ نیز بیانگر مقدار پیش‌بینی شده سری در زمان t توسط هموارسازی نمایی است. به این ترتیب میانگین وزنی بین مقدار واقعی و پیش‌بینی در زمان t برای زمان t+۱ سری زمانی در نظر گرفته می‌شود.

مشخص است که در این رابطه $$\alpha$$ عامل یا فاکتور هموارسازی است. مقدار این عامل در بازه بین ۰ و ۱ قرار دارد. از طرفی با افزایش میزان این فاکتور نقش مشاهدات گذشته در محاسبه و پیش‌بینی مقدارهای آینده کاهش می‌یابد. در حقیقت فاکتور $$\alpha$$ نرخ تاثیر گذاری مقدارهای گذشته را تعیین می‌کند.

در نمودار زیر هموارسازی نمایی با استفاده از فاکتور $$\alpha=0.3$$ و $$\alpha=0.05$$ نمایش داده شده است. همانطور که مشخص است زمانی که مقدار $$\alpha$$‌ کم است، هموارسازی بیشتر صورت گرفته است. با انتخاب $$\alpha=0$$ در حقیقت هموارسازی به صورت میانگین متحرک در خواهد آمد.

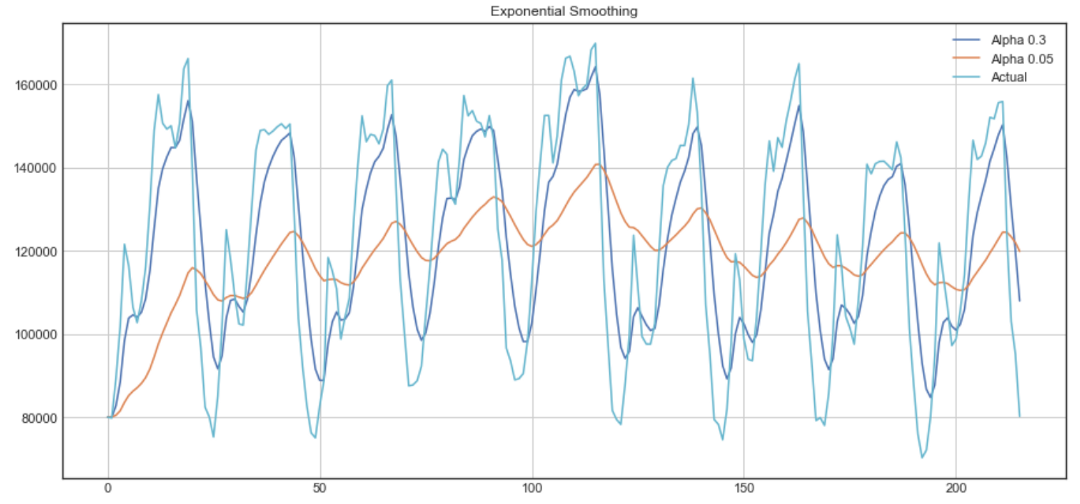
خط سبز در این نمودار مقدارهای واقعی سری زمانی است در حالیکه خط آبی و نارنجی به ترتیب با فاکتور 0.3 و 0.05 هموارسازی را انجام داده‌اند.

نکته: استفاده از هموارسازی نمایی برای سری زمانی بدون روند مناسب به نظر می‌رسد. وجود تناوب در این حالت مشکلی ایجاد نمی‌کند.

هموارسازی نمایی مضاعف (Double Exponential Smoothing)

اگر سری زمانی دارای روند باشند، استفاده از روش هموارسازی نمایی مضاعف نتایج بهتری را ارائه خواهد داد. به نظر می‌رسد که می‌توان هموارسازی نمایی مضاعف را به صورت دو بار استفاده از هموارسازی نمایی ساده در نظر گرفت. شکل رابطه‌ ریاضی آن در زیر قابل مشاهده است.

$$\large y_t=\alpha x_t+(1-\alpha)(y_{t-1}+b_{t-1});\\\large b_t=\beta(y_t-y_{t-1})+(1-\beta)b_{t-1}$$

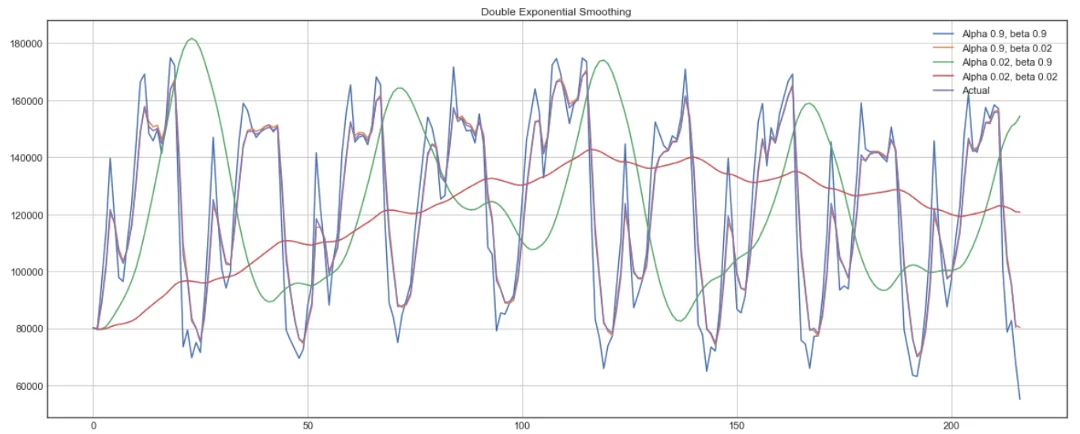
در این رابطه، منظور از $$\beta$$ فاکتور هموارسازی روند است که می‌تواند مانند $$\alpha$$ مقداری بین ۰ تا ۱ داشته باشد. در نمودار زیر با توجه به مقدارهای مختلف برای Alpha و Beta عمل هموارسازی صورت گرفته است.

همانطور که مشخص است با انتخاب مقدارهای کوچک برای Alpha و Beta، هموارسازی به خوبی صورت گرفته است ولی در مقابل با انتخاب Alpha=0.9 و beta=0.02 و beta=0.9 بهترین پیش‌بینی‌ها حاصل شده است. مشخص است با این فاکتورها پیش‌بینی مقدارهای مشاهده شده با مقدار واقعی فاصله کمی داشته ولی امکان پیش‌بینی برای زمان‌های آینده به خوبی صورت نخواهد گرفت. بنابراین استفاده از محاسبات مربوط به خط روند، ابزار بهتری برای پیش‌بینی آینده محسوب می‌شود.

نکته: استفاده از هموارسازی نمایی مضاعف برای سری زمانی بدون تغییرات فصلی مناسب به نظر می‌رسد. وجود تناوب و روند در این حالت مشکلی ایجاد نمی‌کند.

هموارسازی نمایی سه‌تایی (Triple Exponential Smoothing)

با اضافه شدن فاکتور یا عامل هموارسازی فصلی، می‌توان برای سری‌های زمانی فصلی نیز مدلی ارائه داد. مدل ریاضی برای چنین روشی در ادامه دیده می‌شود. همانطور که مشخص است از سه فاکتور همزمان ($$\alpha$$, $$\beta$$ , $$\gamma$$) برای هموارسازی یا پیش‌بینی سری زمانی استفاده شده است.

$$\large y_t=\alpha\dfrac{x_t}{c_{t-L}}+(1-\alpha)(y_{t-1}+b_{t-1});\\\large b_t=\beta(y_t-y_{t-1})+(1-\beta)b_{t-1}\\ \large c_t=\gamma \dfrac{x_t}{y_t}+(1-\gamma)c_{t-L}$$

به $$\gamma$$ پارامتر یا فاکتور هموارسازی فصلی می‌گویند. $$L$$ نیز طول دوره یا بازه زمانی فصل‌ها است.

مدل میانگین متحرک خود همبسته یکپارچه فصلی (SARIMA)

مدل SARIMA (محفف Seasonal Autoregressive Integrated Moving Average Model) را می‌توان ترکیبی از یک مدل پیچیده و ساده در نظر گرفت که می‌تواند برای سری‌های زمانی ناایستا و با تغییرات فصلی به کار گرفته شود. در حالت پیچیده اولیه، مدل «خودهمبسته» (Autoregressive -AR) با مرتبه p استفاده می‌شود. این مدل در حقیقت اجرای رگرسیون است که متغیر مستقل و وابسته هر دو داده‌های سری زمانی را تشکیل می‌دهند. به این ترتیب مقدار حال حاضر سری زمانی وابسته به مقادیر گذشته در نظر گرفته می‌شود. این کار براساس مقدار تاخیر یا Lag برابر با p صورت می‌گیرد. به این معنی که مقدار حاصل حاضر با استفاده از یک رگرسیون خطی براساس p مقدار قبلی انجام می‌شود.

فیلم آموزش کاربرد چندجمله ای و عملگرهای تاخیری در تحلیل سری های زمانی (رایگان) در فرادرس

کلیک کنید

تعیین مقدار مناسب برای پارامتر p توسط تابع و ضریب همبستگی جزئی تعیین می‌شود. همانطور که در نمودار زیر می‌بینید با در نظر گرفتن درجه ۴ برای تاخیرها، میزان تابع خودهمبستگی به صفر می‌رسد بنابراین می‌توان پارامتر p را برابر با ۴ در نظر گرفت.

از طرف دیگر مدل ساده «میانگین متحرک» (Moving Average یا MA) نیز به مدل قبلی افزوده می‌شود. پارامتر این مدل را به صورت q نشان می‌دهند. برای برآورد این پارامتر از تابع و نمودار خود همبستگی استفاده می‌شود. این پارامتر  بزرگترین تاخیری را نشان می‌دهد که از آن به بعد میزان خود همبستگی به صفر نزدیک می‌شود. در تصویر زیر این مقدار برابر با ۴ است.

سپس پارامتر درجه یکپارچگی (Integrated -I) را به مدل اضافه می‌کنیم. پارامتر این مدل را با d نشان می‌دهند که میزان بزرگترین فاصله یا اختلافی است که باعث ایستا شدن سری زمانی در روش هموارسازی میانگین متحرک است.

در مرحله آخر نیز مولفه تغییرات فصلی (Seasonality) را به مدل اضافه می‌کنیم. پارامترهای این مولفه به صورت P,D,Q,s هستند. s نیز طول فصل‌ها را مشخص می‌کند. از طرفی پارامترهای P و Q نیز مانند p و q در مدل MA و AR با توجه به تغییرات فصلی تعیین می‌شوند. در انتها نیز پارامتر D به عنوان پارامتر یکپارچه‌سازی فصلی برای حذف تغییرات فصلی به مدل اضافه می‌شود. به این ترتیب یک مدل SARIMA را به صورت زیر نمایش می‌دهند.

(SARIMA(p,d,q)(P,D,Q,s

نکته اصلی در این گونه تحلیل‌ها، حذف اثرات تغییرات فصلی و روند یا رفتار ناایستا در سری زمانی است تا بتوان مدل SARIMA را به کار گرفت.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌بینی و تحلیل سری‌های زمانی
• آموزش تحلیل و پیش‌بینی سری های زمانی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های کاربردی شبکه های عصبی مصنوعی
• آموزش متلب با نگرش تحلیل آماری، تحلیل سری های زمانی و داده های مکانی
• آموزش کاربرد چندجمله ای و عملگرهای تاخیری در تحلیل سری های زمانی

^^