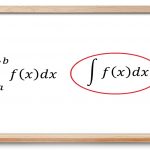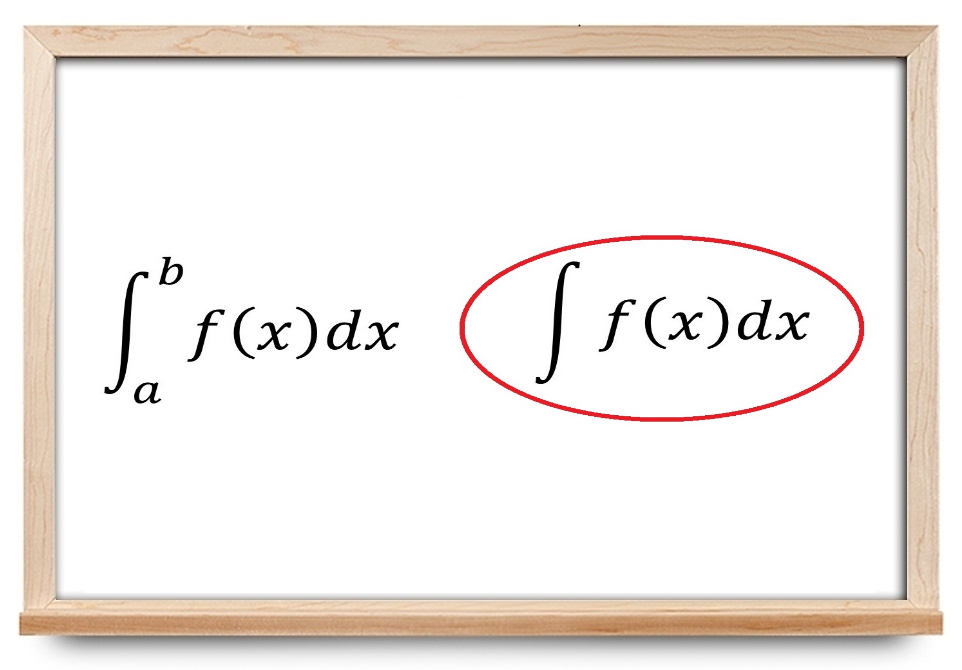انتگرال نامعین — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های پیشین مجله فرادرس، مفاهیم انتگرال و روش‌های انتگرال‌گیری را بیان کردیم. در این آموزش، با مفاهیم انتگرال نامعین آشنا می‌شویم و چند مثال متنوع را بیان می‌کنیم.

پادمشتق و انتگرال نامعین

تابع $$f ( x )$$ را در نظر بگیرید که روی بازه $$I$$ تعریف شده است. تابع $$F ( x )$$ یک پادمشتق $$f ( x)$$ نامیده می‌شود، اگر برای همه $$x$$های روی بازه $$I$$، داشته باشیم:

$$\large { F ^ \prime \left ( x \right ) = f \left ( x \right ) }$$

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

برای تابع $$f (x )$$ تعداد بینهایتی پادمشتق وجود دارد که با هم در ثابت $$C$$ تفاوت دارند:

$$\large { \left ( { F \left ( x \right ) + C } \right ) ^ \prime = F ^ \prime \left ( x \right ) + C ^ \prime } = { f \left ( x \right ) + 0 } = { f \left ( x \right ) . }$$

مجموعه همه پادمشتق‌های تابع $$f ( x)$$، انتگرال نامعین $$f ( x)$$ نامیده می‌شود و به صورت زیر بیان می‌گردد:

$$\large { { \int } { { f \left ( x \right ) } { d x } } } = { F \left ( x \right ) + C , \; \; } \kern0pt{\text{if} \; \; F ^ \prime \left ( x \right ) = f \left ( x \right ) . }$$

در این تعریف، $$\int$$ نماد انتگرال، $$f ( x)$$ انتگرالده، $$x$$ متغیر انتگرال‌گیری، $$d x$$ دیفرانسیل متغیر $$x$$ و $$C$$ ثابت انتگرال‌گیری نامیده می‌شود.

انتگرال نامعین توابع رایج

انتگرال‌گیری فرایند معکوس مشتق‌گیری است، بنابراین، جدول انتگرال‌های پایه از جدول مشتق‌های پایه تبعیت می‌کند.

در جدول زیر فهرستی از انتگرال‌های نامعین مهم ارائه شده است.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

ویژگی‌های انتگرال نامعین

دو ویژگی مهم انتگرال نامعین به صورت زیر است که در محاسبه آن‌ها کاربرد فراوانی دارند:

۱. اگر $$a$$ یک عدد ثابت باشد، آنگاه داریم:

$$ \large \cssId{element11} { \int { a f \left ( x \right ) d x } } = \cssId{element12} { a \int { f \left ( x \right ) d x } } $$

یعنی ضریب ثابت را می‌توان از انتگرال بیرون آورد.

2. برای توابع $$f ( x )$$ و $$g ( x)$$، رابطه زیر برقرار است:

$$ \large \cssId{element13} { \int { \left [ { f \left ( x \right ) \pm g \left ( x \right ) } \right ] d x } } = \cssId{element14} { \int { f \left ( x \right ) d x } } \pm \cssId{element15} { \int { g \left ( x \right ) d x } } $$

یعنی انتگرال نامعین مجموع (یا تفاضل) دو تابع، برابر با مجموع (یا تفاضل) انتگرال آن دو تابع است.

محاسبه انتگرال‌ها با استفاده از ویژگی‌های خطی انتگرال نامعین و استفاده از جدول انتگرال‌های اصلی، انتگرال‌گیری مستقیم نام دارد.

مثال‌هایی از محاسبه انتگرال نامعین

در این بخش چند مثال را از محاسبه انتگرال نامعین بررسی می‌کنیم.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

مثال ۱

حاصل انتگرال نامعین $${\int {\left( {3{x^2} – 6x + 2\cos x} \right)dx} }$$ را به دست آورید.

حل: با استفاده از ویژگی‌های ۱ و ۲، داریم:

$$\large \begin {align*} I & = \int { \left ( { 3 { x ^ 2 } – 6 x + 2 \cos x } \right ) d x } \\ & = { \int { 3 { x ^ 2 } d x } } - { \int { 6 x d x } } + { \int { 2 \cos x d x } } \\ & = { 3 { \int { { x ^2 } d x } } } - { 6 { \int { x d x } } } + { 2 { \int { \cos x d x } } . } \end {align*}$$

حاصل هر سه انتگرال را با استفاده از جدول بالا می‌نویسیم و در نهایت، خواهیم داشت:

$$\large \begin{align*} I & = 3 \cdot { \frac { { { x ^ 3 } } } { 3 } } - { 6 \cdot { \frac { { { x ^ 2 } } } { 2 } } } + { 2 \cdot { \sin x } + C } \\ & = { { { x ^ 3 } } - { 3 { x ^ 2 } } + { 2 \sin x + C . } } \end {align*}$$

مثال ۲

انتگرال نامعین $$\int {\left( {1 + x} \right)\left( {1 + 2x} \right)dx}$$ را محاسبه کنید.

حل: انتگرالده را به صورت زیر ساده می‌کنیم:

$$\large { \left ( { 1 + x } \right ) \left ( { 1 + 2 x } \right ) } ={ 1 + x + 2 x + 2 { x ^ 2 } } = { 2 { x ^ 2 } + 3 x + 1 . }$$

و حاصل انتگرال به صورت زیر محاسبه می‌شود:

$$\large \begin {align*} & \int { \left ( { 1 + x } \right ) \left ( { 1 + 2 x } \right ) d x } = { \int { \left ( { 2 { x ^ 2 } + 3 x + 1 } \right ) d x } } \\ & = { \int { 2 { x ^ 2 } d x } } + { \int { 3 x d x } } + { \int { 1 d x } } = { 2 \int { { x ^ 2 } d x } } + { 3 \int { x d x } } + { \int { d x } } \\ & = { 2 \cdot \frac { { { x ^ 3 } } } { 3 } } + { 3 \cdot \frac { { { x ^ 2 } } } { 2 } } + { x + C } = { \frac { { 2 { x ^ 3 } } } { 3 } + \frac { { 3 { x ^ 2 } } } { 2 } + x + C . } \end {align*}$$

مثال ۳

حاصل انتگرال نامعین $$\int {\left( {\large{\frac{1}{{{x^2}}}}\normalsize – \large{\frac{1}{{{x^3}}}}\normalsize} \right)dx}$$ را به دست آورید.

حل: با استفاده از قانون جمع، می‌نویسیم:

$$\large { I = \int { \left ( { \frac { 1 } { { { x ^ 2 } } } – \frac { 1 } { { { x ^ 3 } } } } \right ) d x } } = { \int { \frac { { d x } } { { { x ^ 2 } } } } – \int { \frac { { d x } } { { { x ^ 3 } } } } . }$$

انتگرالده‌های دو انتگرال توابعی توانی هستند؛ بنابراین، می‌توان نوشت:

$$\large \begin {align*} I & = \int { { x ^ { – 2 } } d x } – \int { { x ^ { – 3 } } d x } = { \frac { { { x ^ { – 1 } } } } { { \left ( { – 1 } \right ) } } } - { \frac { { { x ^ { – 2 } } } } { { \left ( { – 2 } \right ) } } + C } \\ & = { – \frac { 1 } { x } + \frac { 1 } { { 2 { x ^ 2 } } } + C . } \end {align*}$$

مثال ۴

حاصل انتگرال نامعین $$\int { \left ( { \sqrt x + \sqrt [ \large 3 \normalsize ] { x } } \right ) d x }$$ را به دست آورید.

حل:

$$\large \begin {align*} \int { \left ( { \sqrt x + \sqrt [ \large 3 \normalsize ]{ x } } \right ) d x } & = { \int { \sqrt x d x } + \int { \sqrt [ \large 3 \normalsize ] { x } d x } } = { \int { { x ^ { \large \frac { 1 } { 2 } \normalsize } } d x } + \int { { x ^ { \large \frac { 1 } { 3 } \normalsize } } d x } } \\ & = { \frac { { { x ^ { \large \frac { 1 } { 2 } \normalsize + 1 } } } } { { \frac { 1 } { 2 } + 1 } } + \frac { { { x ^ { \large \frac { 1 } { 3 } \normalsize + 1 } } } } { { \frac { 1 } { 3 } + 1 } } + C } = { \frac { { 2 { x ^ { \large \frac { 3 }{ 2 } \normalsize } } } } { 3 } + \frac { { 3 { x ^ { \large \frac { 4 }{ 3 } \normalsize } } } } { 4 } + C}  \\ & = { \frac { { 2 \sqrt { { x ^ 3 } } } } { 3 } + \frac { { 3 \sqrt [ \large 3 \normalsize ]{ { { x ^ 4 } } } } } { 4 } + C . } \end {align*}$$

مثال ۵

حاصل انتگرال نامعین $$\int { \large { \frac { { x + 1 } } { { \sqrt x } } } \normalsize d x }$$ را به دست آورید.

حل: انتگرال را به صورت مجموع دو انتگرال می‌نویسیم و سپس آن‌ها را به طور جداگانه محاسبه می‌کنیم:

$$\large \begin {align*} { \int { \frac { { x + 1 } } { { \sqrt x } } d x } } & = { \int { \left ( { \frac { x } { { \sqrt x } } + \frac { 1 } { { \sqrt x } } } \right ) d x } } = { \int { \left ( { \sqrt x + \frac { 1 } { { \sqrt x } } } \right ) d x } } \\ & = { \int { \sqrt x d x } + \int { \frac { { d x } } { { \sqrt x } } } } = { \frac { { { x ^ { \frac { 3 } { 2 } } } } } { { \frac { 3 } { 2 } } } + 2 \sqrt x + C } \\ & = { \frac { { 2 \sqrt { { x ^ 3 } } } } { 3 } + 2 \sqrt x + C . } \end {align*}$$

مثال ۶

انتگرال نامعین $$\int {{{\left( {x + \sqrt x } \right)}^2}dx}$$ را محاسبه کنید.

حل: توان دوم انتگرالده را اعمال کرده و جملات را بسط می‌دهیم:

$$\large \begin {align*} I & = \int { { { \left ( { x + \sqrt x } \right ) } ^ 2 } d x } = { \int { \left ( { { x ^ 2 } + 2 x \sqrt x + { { \left ( { \sqrt x } \right ) } ^ 2 } } \right ) d x } } \\ &= { \int { \left ( { { x ^ 2 } + 2 { x ^ { \frac { 3 } { 2 } } } + x } \right ) d x } . } \end {align*}$$

با توجه به ویژگی‌های اساسی انتگرال، داریم:

$$\large \begin {align*} I & = \int { \left ( { { x ^ 2 } + 2 { x ^ { \frac { 3 } { 2 } } } + x } \right ) d x } \\ & = { \int { { x ^ 2 } d x } } + { 2 \int { { x ^ { \frac { 3 } {2 } } } d x } } + { \int { x d x } . } \end {align*}$$

با کمک جدول انتگرال‌ها، به راحتی می‌توانیم انتگرال‌ها را محاسبه کنیم و خواهیم داشت:

$$\large \begin {align*} I & = \frac { { { x ^ 3 } } } { 3 } + 2 \cdot \frac { { { x ^ { \frac { 5 } { 2 } } } } } { { \frac { 5 } { 2 } } } + \frac { { { x ^ 2 } } } { 2 } + C \\ &= { \frac { { { x ^ 3 } } } { 3 } + \frac { { 4 { x ^ { \frac { 5 } { 2 } } } } } { 5 } + \frac { { { x ^ 2 } } } { 2 } + C } \\ & = { \frac { { { x ^ 3 } } } { 3 } + \frac { { 4 \sqrt { { x ^ 5 } } } } { 5 } + \frac { { { x ^ 2 } } } { 2 } + C . } \end {align*}$$

مثال ۷

انتگرال نامعین $$\int {\left( {\large\frac{3}{{\sqrt[\large 3\normalsize]{x}}}\normalsize + \large\frac{2}{{\sqrt x }}\normalsize} \right)dx}$$ را محاسبه کنید.

حل: با استفاده از قانون توان انتگرال، داریم:

$$\large \begin {align*} { \int { \left ( { \frac { 3 } { { \sqrt [ \large 3 \normalsize ]{ x } } } + \frac { 2 } { { \sqrt x } } } \right ) d x } } & = { \int { \frac { { 3 d x } } { { \sqrt [ \large 3 \normalsize ] { x } } } } + \int { \frac { { 2 d x } } { { \sqrt x } } } } = { 3 \int { { x ^ { – \large \frac { 1 } { 3 } \normalsize } } d x } + 2 \int { { x ^ { – \large \frac { 1 } { 2 } \normalsize } } d x } } \\ & = { 3 \cdot \frac { { { x ^ { – \large \frac { 1 } { 3 } \normalsize + 1 } } } } { { – \large \frac { 1 } { 3 } \normalsize + 1}} }+{ 2 \cdot \frac { { { x ^ { – \large \frac { 1 } { 2 } \normalsize + 1 } } } } { { – \frac { 1 } { 2 } + 1 } } } + { C } \\ & = { \frac { { 9 { x ^ { \large \frac { 2 } { 3} \normalsize } } } } { 2 } + 4 { x ^ { \large \frac { 1 } { 2 } \normalsize } } + C } = { \frac { { 9 \sqrt [ \large 3 \normalsize ] { { { x ^ 2 } } } } } { 2 } + 4 \sqrt x + C . } \end {align*}$$

مثال ۸

انتگرال نامعین $$\int {\left( {\sqrt[3]{x} + {e^3}} \right)dx}$$ را محاسبه کنید.

حل: با توجه به ویژگی‌های اساسی انتگرال‌ می‌توان نوشت:

$$\large \begin {align*} I & = \int { \left ( { \sqrt [ 3 ] { x } + { e ^ 3 } } \right ) d x } = { \int { \left ( { { x ^ { \frac { 1 } { 3 } } } + { e ^ 3 } } \right ) d x } } \\ & = { \int { { x ^ { \frac { 1 } { 3 } } } d x } + \int { { e ^ 3 } d x } } = { \int { { x ^ { \frac { 1 }{ 3 } } } d x } + { e ^ 3 } \int { d x } . } \end {align*}$$

در انتگرال سوم، $$e ^ 3$$ یک ثابت است، بنابراین، آن را از داخل انتگرال بیرون می‌آوریم. در نتیجه، خواهیم داشت:

$$\large \begin {align*} I & = \int { { x ^ { \frac { 1 } { 3 } } } d x } + { e ^ 3 } \int { d x } = { \frac { { { x ^ { \frac { 4 } { 3 } } } } } { { \frac { 4 } { 3 } } } + { e ^ 3 } x + C } \\ & = { \frac { { 3 \sqrt [ 3 ] { { { x ^ 4 } } } } } { 4 } + { e ^ 3 } x + C . } \end {align*}$$

مثال ۹

عبارت $$\int {\large\frac{{4dx}}{{2 + 3{x^2}}}\normalsize}$$ را محاسبه کنید.

حل: از جدول انتگرال و به طور خاص، $$\int { \large \frac { { d x } } { { { a ^ 2 } + { x ^ 2 } } } \normalsize } = { \large \frac { 1 } { a } \normalsize } \arctan { \large \frac { x } { a } \normalsize } + C$$ استفاده می‌کنیم. در نتیجه، خواهیم داشت:

$$\large \begin {align*} \int { \frac { { 4 d x } } { { 2 + 3 { x ^ 2 } } } } & = { 4 \int { \frac { { d x } } { { 3 \left ( { \frac { 2 } { 3 } + { x ^ 2 } } \right ) } } } } = { \frac { 4 } { 3 } \int { \frac { { d x } } { { { { \left ( { \sqrt { \frac { 2 } { 3 } } } \right ) } ^ 2 } + { x ^ 2 } } } } } \\ & = { \frac { 4 } { 3 } \cdot \frac { 1 } { { \sqrt { \frac { 2 } { 3 } } } } \arctan \frac { x } { { \sqrt { \frac { 2 } { 3 } } } } } + { C } = { \frac { 4 } { { \sqrt 6 } } \arctan \frac { { \sqrt 3 x } } { { \sqrt 2 } } } + { C . } \end {align*}$$

مثال ۱۰

انتگرال نامعین $$\int {\large{\frac{{{x^2}}}{{1 + {x^2}}}}\normalsize dx}$$ را محاسبه کنید.

حل: این انتگرال را به صورت جمع دو انتگرال می‌نویسیم:

$$\large \begin {align*} I & = \int { \frac { { { x ^ 2 } } } { { 1 + { x ^ 2 } } } d x } = \int { \frac { { 1 + { x ^ 2 } – 1 } } { { 1 + { x ^ 2 } } } d x } = { \int { \left ( { \frac { { 1 + { x ^ 2 } } } { { 1 + { x ^ 2 } } } } - { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) d x } } \\ & = { \int { \left ( { 1 – \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) d x } } = { \int { d x } } - { \int { \frac { { d x } } { {1 + { x ^ 2 } }} } .} \end {align*}$$

در نتیجه، خواهیم داشت:

$$\large { I = \int { d x } – \int { \frac { { d x } } { { 1 + { x ^ 2 } } } } } = { x – \arctan x + C . }$$

مثال ۱۱

انتگرال نامعین $$\int {\large{\frac{{dx}}{{1 + 2{x^2}}}}\normalsize}$$ را محاسبه کنید.

حل: می‌توانیم انتگرال را به صورت زیر بنویسیم:

$$\large \begin {align*} I & = \int { \frac { { d x } } { { 1 + 2 { x ^ 2 } } } } = { \int { \frac { { d x } } { { 2 \left ( { \frac { 1 } { 2 } + { x ^ 2 } } \right ) } } } } \\ & = { \frac { 1 } { 2 } \int { \frac { { d x } }{ { \frac { 1 } { 2 } + { x ^ 2 } } } } } = { \frac { 1 } { 2 } \int { \frac { { d x } } { { { { \left ( { \frac { 1 } { { \sqrt 2 } } } \right ) } ^ 2 } + { x ^ 2 } } } } . } \end {align*}$$

با استفاده از انتگرال $$\int {\large\frac{{dx}}{{{a^2} + {x^2}}}\normalsize} = {\large\frac{1}{a}\normalsize}\arctan {\large\frac{x}{a}\normalsize}$$، داریم:

$$\large \begin {align*} I & = \frac { 1 } { 2 } \int { \frac { { d x } } { { { { \left( { \frac { 1 } { { \sqrt 2 } } } \right ) } ^ 2 } + { x ^ 2 } } } } = { \frac { 1 } { 2 } \cdot \frac {1 } { { \frac { 1 } { { \sqrt 2 } } } } \arctan \frac { x } { { \frac { 1 } { { \sqrt 2 } } } } + C }\\ & = { \frac { { \sqrt 2 } } { 2 } \arctan \left ( { \sqrt 2 x } \right ) + C } = { \frac { 1 } { { \sqrt 2 } } \arctan \left ( { \sqrt 2 x } \right ) + C . } \end {align*}$$

مثال ۱۲

حاصل انتگرال نامعین $$\int {\large\frac{{\pi dx}}{{\sqrt {\pi – {x^2}} }}\normalsize}$$ را بیابید.

حل: با استفاده از انتگرال $$\int {\large\frac{{dx}}{{\sqrt {{a^2} – {x^2}} }}\normalsize}= \arcsin {\large\frac{x}{a}\normalsize} + C$$، خواهیم داشت:

$$\large { \int { \frac { { \pi d x } } { { \sqrt { \pi – { x ^ 2 } } } } } } = { \pi \int { \frac { { d x } } { { \sqrt { { { \left ( { \sqrt \pi } \right ) } ^ 2 } – { x ^ 2 } } } } } } = { \pi \arcsin \frac { x } { { \sqrt \pi } } + C . }$$

مثال ۱۳

حاصل انتگرال $$\int { \left ( { 2 \cos x – 5 \sin x } \right ) d x }$$ را به دست آورید.

حل: با استفاده از قاعده جمع، قاعده ضریب ثابت و جدول انتگرال‌های پایه، داریم:

$$\large \begin {align*} \int { \left ( { 2 \cos x – 5 \sin x } \right ) d x } & = { \int { 2 \cos x d x } } - { \int { 5 \sin x d x } } \\ &= { 2 \int { \cos x d x } } - { 5 \int { \sin x d x } } \\ &= { 2 \cdot \sin x } - { 5 \cdot \left ( { – \cos x } \right ) + C } \\ & = { 2 \sin x + 5 \cos x + C . } \end {align*}$$

مثال ۱۴

حاصل انتگرال نامعین $$\int {\large{\frac{{dx}}{{\sqrt {1 – \large{\frac{{{x^2}}}{2}}\normalsize} }}}\normalsize}$$ را محاسبه کنید.

حل: از چند عمل جبری ساده استفاده می‌کنیم و انتگرال را به فرم استاندارد می‌نویسیم:

$$\large \begin {align*} I & = \int { \frac { { d x } } { { \sqrt { 1 – \frac { { { x ^ 2 } } } { 2 } } } } } = { \int { \frac { { d x } } { { \sqrt { \frac { 1 } { 2 } \left ( { 2 – { x ^ 2 } } \right ) } } } } } \\ & = { \int { \frac { { d x } } { { \sqrt { \frac { 1 } { 2 } } \sqrt { 2 – { x ^ 2 } } } } } } = { \sqrt 2 \int { \frac { { d x } } { { \sqrt { 2 – { x ^ 2 } } } } } } \\ & = { \sqrt 2 \int { \frac { { d x } } { { \sqrt { { { \left ( { \sqrt 2 } \right ) } ^ 2 } – { x ^ 2 } } } } } . } \end {align*}$$

بسط بالا شامل انتگرال $$\int { \large \frac { { d x } } { { \sqrt { { a ^ 2 } – { x ^ 2 } } } } \normalsize } = \arcsin { \large \frac { x } { a } \normalsize }$$ است. بنابراین، خواهیم داشت:

$$\large { I = \sqrt 2 \int { \frac { { d x } } { { \sqrt { { { \left ( { \sqrt 2 } \right ) } ^ 2 } – { x ^ 2 } } } } } } = { \sqrt 2 \arcsin \frac { x } {{ \sqrt 2 } } + C . }$$

مثال ۱۵

انتگرال نامعین $$\int {{{\tan }^2}xdx}$$ را محاسبه کنید.

حل: از آنجایی که $${ \tan ^ 2 } x = { \sec ^ 2 } x – 1$$، انتگرال برابر است با:

$$\large \begin {align*} & \int { { { \tan } ^ 2 } x d x } = { \int { \left ( { { { \sec } ^ 2 } x – 1 } \right ) d x } } \\ & = { \int { { { \sec } ^ 2 } x d x } – \int { d x } } = { \tan x – x + C . } \end {align*}$$

مثال ۱۶

انتگرال نامعین $$\int {{{\cot }^2}xdx}$$ را محاسبه کنید.

حل: از اتحاد مثلثاتی زیر استفاده می‌کنیم:

$$\large { \frac { 1 } { { { { \sin } ^ 2 } x } } – { \cot ^ 2 } x = 1 , } \; \; \Rightarrow { { \cot ^ 2 } x = \frac { 1 } { { { { \sin } ^ 2 } x } } – 1 . }$$

در نتیجه، می‌توان این انتگرال نامعین را به صورت مجموع دو انتگرال نوشت:

$$\large { I = \int { { { \cot } ^ 2 } x d x } = \int { \left ( { \frac { 1 } { { { { \sin } ^ 2 } x } } – 1 } \right ) d x } } = { \int { \frac { { d x } } { { { { \sin } ^ 2 } x } } } – \int { d x} .}$$

بنابراین، خواهیم داشت:

$$\large { I = \int { \frac { { d x } } { { { { \sin } ^ 2 } x } } } – \int { d x } } = { – \cot x – x + C . }$$

مثال ۱۷

حاصل انتگرال نامعین $$\int {\large\frac{{dx}}{{{\sin^2}2x}}\normalsize}$$ را بدون استفاده از تغییر متغیر به دست آورید.

حل: با استفاده از فرمول زاویه دو برابر $$\sin 2 x= 2 \sin x \cos x$$ و اتحاد $${ \sin ^ 2 } x + { \cos ^ 2 } x = 1$$، می‌توان نوشت:

$$\large \begin {align*} & \int { \frac { { d x } } { { { \sin ^ 2 } 2 x } } } = { \frac { 1 } { 4 } \int { \frac { { d x } } { { { \sin ^ 2 } x { { \cos } ^ 2 } x } } } } = { \frac { 1 } { 4 } \int { \frac { { \left ( { { { \sin } ^ 2 } x + { { \cos } ^ 2 } x } \right ) d x } } { { { \sin ^ 2 } x { { \cos } ^ 2 } x } } } } \\ & = { \frac { 1 } { 4 } \int { \left ( { \frac { 1 } { { { { \cos } ^2 } x } } } \right . } + { \left . { \frac { 1 } { { { \sin ^ 2 } x } } } \right ) d x } } = { \frac { 1 } { 4 } \int { { { \sec } ^ 2 } x d x } } + { \frac { 1 } { 4 } \int { { \csc ^ 2 } x d x } }\\ & = { \frac { 1 } { 4 } \tan x – \frac { 1 } { 4 } \cot x } + { C } = { \frac { 1 } { 4 } \left ( { \tan x – \cot x } \right ) } + { C . } \end {align*}$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضی عمومی ۱ (همراه با حل مثال و تست کنکور کارشناسی ارشد)
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش ریاضی عمومی ۲
• انتگرال گاوسی — از صفر تا صد
• انتگرال دوگانه — به زبان ساده
• تقلب نامه (Cheat Sheet) فرمول های انتگرال

^^