آموزش روش AHP یا تحلیل سلسله مراتبی | به زبان ساده

در دنیایی با پیچیدگی روزافزون، اتخاذ بهترین تصمیمات به مسئله دشواری برای مدیران شرکت‌ها، سازمان‌های دولتی، سیاست‌گذاران و سایر تصمیم‌گیرندگان تبدیل شده است و آن‌ها ترجیح می‌دهند از ابزارهای تحلیلی و کمی استفاده کنند. یکی از این ابزار‌ها، فرایند تحلیل سلسله‌مراتبی یا بهره‌گیری از روش AHP است. در این نوشتار، به صورت اجمالی و به همراه مثال به معرفی روش AHP می‌پردازیم.

روش AHP چیست؟

به صورت کلی، «فرایند تحلیل سلسه مراتبی» یا روش (Analytical Hierarchy Process | AHP) نظریه‌ای بر پایه «سنجش نسبی» (Relative Measurement) است. در این روش، از تکنیکی ساختارمند (بر پایه اصول ریاضی و روانشناسی) برای نظم‌دهی و تحلیل تصمیمات پیچیده استفاده می‌شود. این روش توسط «توماس ساعتی» (Thomas Saaty) - استاد شناخته‌شده عراقی - در دهه ۱‍۹۷۰ میلادی بوجود آمد. در فرایند تحلیل سلسله مراتبی، از روشی دقیق برای کمی کردن وزن‌های معیار‌های تصمیم‌گیری بکارگرفته می‌شود.

سنجش نسبی چیست؟

در سنجش نسبی، تمرکز روی اندازه‌گیری دقیق مقادیر نیست بلکه نسبت‌های بین آن‌ها بررسی می‌شود. یک جفت سنگ را در نظر بگیرید. در اندازه‌گیری معمولی ممکن است به دانستن وزن دقیق این سنگ‌ها توجه شود و در صورتی اندازه‌گیری (۲،۱) صحیح است که سنگ اول، ۲ کیلوگرم و سنگ دوم، ۱ کیلوگرم وزن داشته باشند.

در سنجش نسبی، به دانستن سنگینی هر شی در مقایسه با شی دیگر توجه می‌شود. در نتیجه، جفت اندازه‌گیری (۲،۱) زمانی صحیح است که وزن سنگ اول، دو برابر سنگ دوم باشد. در این مثال، درصورت بکارگیری سنجش نسبی، جفت‌های اندازه‌گیری (۱/۳ ،۲/۳)، (۴،۲) و (۸،۴) نیز برای این دو سنگ صدق می‌کنند.

بهترین کاربرد روش سنجش نسبی چیست؟

بهترین کاربرد روش سنجش نسبی، در مسائلی است که باید بهترین جایگزین روش فعلی، انتخاب شود. به علاوه، در زمان غیرملموس بودن ویژگی‌های گزینه، استفاده از معیار اندازه‌گیری دشوار است و اندازه‌گیری نسبی، فرایند را تسهیل می‌کند. روش AHP با انجام مقایسه‌های زوجی (جفت به جفت) بین گزینه‌‌ها آن‌ها را رتبه‌بندی می‌کند.

یکی از مهم‌ترین کاربرد‌های AHP، بکارگیری آن در نواحی غیرعینی است. در نتیجه، از آن برای حل مسائل تصمیم‌گیری چند معیاره (Multi-criteria Decision Making | MCDM) استفاده می‌شود که در آن گزینه‌ها با توجه به چندین معیار بررسی می‌شوند.

خصوصیات عینی گزینه‌ها مانند وزن سنگ‌های متفاوت یا حقوق کارمندان مختلف، بدون اعمال نظر شخصی و ابهام قابل اندازه‌گیری هستند. در نتیجه، بکارگیری روش AHP مفید به شمار نمی‌رود. بزرگی بعضی از ویژگی‌های گزینه‌ها مانند چابکی یک ورزشکار یا زیبایی یک پل، به آسانی قابل درک و سنجش نیست. این ویژگی‌ها عینی نیستند و روش AHP در اینجا بیشترین کارایی خود را خواهد داشت.

چگونه از روش AHP استفاده کنیم؟

از روش AHP می‌توان در مسائل تصمیم‌گیری با گزینه‌های محدود استفاده کرد. در یک فرایند تصمیم‌گیری، یک هدف و تعداد محدودی گزینه به صورت زیر وجود دارد که در آن از تصمیم‌گیرنده خواسته شده که بهترین گزینه را انتخاب کند.

$$X=\left\{x_{1},x_{2},x_{3},...,x_{n}\right\}$$

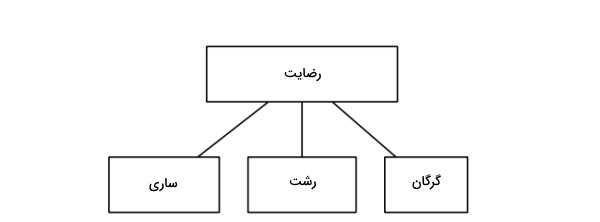
تشریح روش AHP با مثال، آسان‌تر از تشریح نظری آن است. در ادامه به بررسی نمونه‌ای پرداخته‌ایم. فرض کنید که خانواده‌ای قصد دارد برای تعطیلات به یکی از شهر‌های شمالی سفر کند. هدف خانواده کسب بیشترین رضایت و مطلوبیت از سفر است. در اینجا، تصمیم‌گیرنده باید از میان ۳ گزینه گرگان، رشت و ساری به انتخاب بپردازد.

{   گرگان   ،    رشت   ،   ساری  }   =   X

• ساری:$$x_{1}$$
• رشت:$$x_{2}$$
• گرگان:$$x_{3}$$

اغلب، در فرایند‌های تصمیم‌گیری از تصمیم‌گیرنده درخواست می‌شود که به هرکدام از گزینه‌ها نمره‌ای اختصاص دهد و سپس گزینه‌ای با بالاترین ارزش را از میان آن‌ها انتخاب کند.

اگر مجموعه‌ای داده شده از گزینه‌ها به صورت $$X=\left\{x_{1},x_{2},x_{3},...,x_{n}\right\}$$داشته باشیم، تصمیم‌گیرنده باید یک بردار وزن‌دهی به صورت زیر به آن‌ها اختصاص دهد.

$$w=\left(w_{1},...,w_{n}\right)^{T}$$

که در آن $$w_{i}$$ مقداری است که به صورت منسجم، ارزش گزینه $$x_{i}$$ را می‌سنجد. یعنی هرچه $$w_{i}$$ بزرگ‌تر باشد، ارزش گزینه $$i$$ بیشتر است. درواقع، اگر و تنها اگر، $$w_{i}$$ بزرگ‌تر از $$w_{j}$$ باشد،  $$x_{i}$$ به $$x_{j}$$ ترجیح داده می‌شود. بردار وزن‌دهی، همان بردار امتیازدهی است و اجزای آن‌ها الویت‌ها یا وزن‌های گزینه‌ها ($$x_{i}$$ها) هستند.

برای مثال، اگر بردار وزن‌دهی به شکل مقابل داشته باشیم، $$w=\left(0.4,0.2,0.3,0.1\right)^{T}$$یعنی $$x_{1}$$ نسبت به سایر گزینه‌ها برای فرد، اهمیت بیشتری دارد. جایی که $$w_{i}$$ بیشتر از $$w_{j}$$ باشد، یعنی گزینه $$x_{i}$$ به$$x_{j}$$ ترجیح داده شده است.

مثال اول بکارگیری روش AHP

بار دیگر به مثال انتخاب مقصد مسافرتی رجوع کنیم. اگر بردار $$w=\left(0.3,0.5,0.2\right)^{T}$$ برای مجموعه‌ای از گزینه‌های X= { رشت، گرگان، ساری } انتخاب شده باشد، بنابراین الویت انتخاب شهر‌ها به صورت زیر خواهد بود.

ساری  <  رشت < گرگان

زیرا $$w_{2}$$ بیشتر از $$w_{1}$$ بیشتر از $$w_{3}$$ است. تصمیم‌گیری به این روش آسان به نظر می‌رسد اما در صورت افزوده شدن پیچیدگی‌ها، به مسئله‌ای دشوار تبدیل می‌شود. همان‌طور که قابل مشاهده است، پیچیدگی با تعداد گزینه‌ها و معیارها افزایش می‌یابد.

تصمیم‌گیرنده هنگام امتیازدهی عددی، برای فهرستی طولانی از گزینه‌ها، با دشواری مواجه می‌شود. در نهایت، ممکن است موفق به تصمیم‌گیری شود اما بهترین تصمیم ممکن را انتخاب نکند. امکان دارد، این اتفاق، به علت محدودیت‌های شناختی و عدم امکان مقایسه بهینه چندین گزینه به صورت همزمان، رخ دهد.

روشی موثر برای غلبه بر این مشکل بکارگیری «مقایسه زوجی» (Pairwise Comparison) است. این روش امکان مقایسه دو گزینه را در هر زمان بوجود می آورد. در این روش، مسئله اصلی به چند مسئله کوچک‌تر تبدیل می‌شود.

مقایسه‌های دوبه‌دو، به شکل «ماتریس مقایسه زوجی» (Pairwise Comparison Matrix) انجام و این ماتریس به شکل زیر تعریف می‌شود.

$$\mathbf{A}=\left(\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right)$$

در ماتریس بالا، به ازای $$a_{ij}$$>0 میزان ترجیحات از $$x_{i}$$ تا $$x_{j}$$ تعیین می‌شود. به صورت دقیق‌تر، طبق نظریه ساعتی، هر درایه ماتریس نشان‌دهنده نسبت تقریبی بین دو وزن است.

$$\forall i،j$$            $$a_{ij}\approx\frac{w_{i}}{w_{j}}$$

یعنی اگر درایه‌های ماتریس دقیقا نشان‌دهنده نسبت بین وزن‌ها باشند، ماتریس $$A$$ به شکل زیر قابل مشاهده خواهد بود.

$$\mathbf{A}=\left(w_{i} / w_{j}\right)_{n \times n}=\left(\begin{array}{cccc} w_{1} / w_{1} & w_{1} / w_{2} & \ldots & w_{1} / w_{n} \\ w_{2} / w_{1} & w_{2} / w_{2} & \ldots & w_{2} / w_{n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n} / w_{1} & w_{n} / w_{2} & \ldots & w_{n} / w_{n} \end{array}\right)$$

با در نظر گرفتن دو ماتریس گفته شده به ماتریس سوم می‌رسیم به صورتی که $$a_{ij}=1/a_{ji}$$ و ماتریس A می‌تواند به شکل ساده و بازنویسی شده زیر، بیان شود.

$$\mathbf{A}=\left(\begin{array}{cccc} 1 & a_{12} & \cdots & a_{1 n} \\ \frac{1}{a_{12}} & 1 & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{1}{a_{1 n}} & \frac{1}{a_{2 n}} & \cdots & 1 \end{array}\right)$$

به عبارتی دیگر، ساختار ساده شده مقایسه زوجی به این شکل، این فرض را دنبال می‌کند که اگر برای مثال، $$x_{1}$$ دو برابر $$x_{2}$$ بهتر باشد، نتیجه‌گیری می‌کنیم که $$x_{2}$$ به اندازه نصف $$x_{1}$$  خوب است. در اینجا، ادامه مثال مسافرت را بررسی و آن‌را به روش ماتریس مقایسه زوجی تشریح می‌کنیم. در ماتریس زیر، برای سادگی، عناوین $$x_{1}$$، $$x_{2}$$ و $$x_{۳}$$ بر سطر و ستون‌ها درج شده‌اند.

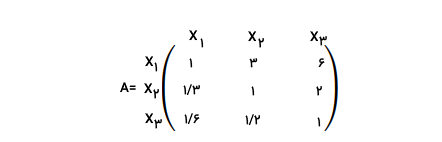
از این ماتریس مخصوص و نهاده $$a_{12}$$ متوجه می‌شویم که $$x_{1}$$  (رشت)، ۳ برابر بهتر از $$x_{2}$$ (گرگان) است. یعنی $$a_{12}$$=3 نشاندهنده $$w_{1}=3w_{2}$$ است. زمانی که ماتریس مقایسه‌ای زوجی کامل شود، از روش‌های متعددی می‌توان به بردار وزن دست پیدا کرد. در این مثال، می‌توان شرط $$a_{ij}=w_{i}/w_{j} \forall i,j$$  را با بردار قرار گرفته در ادامه، بررسی کرد.

$$\mathbf{w}=\left(\begin{array}{l} 6 / 9 \\ 2 / 9 \\ 1 / 9 \end{array}\right)$$

در نتیجه، رشت بهترین گزینه به شمار می‌رود. به صورت خلاصه، زمانی که اعداد گزینه بسیار بزرگ هستند، مقایسه زوجی روشی موثر برای دستیابی به رتبه‌بندی است. رتبه‌بندی گزینه‌های قرارگرفته در بردار $$w$$ قوی‌تر از حالتی است که به صورت مستقیم می‌خواستیم آن‌ها را بدون استفاده از $$A$$ بدست بیاوریم.

از ماتریس مقایسه زوجی تا سلسله‌ مراتب

در اینجا به چرایی پر شدن ماتریس A به صورت انجام شده و عوامل تاثیرگذار بر قضاوت‌های فرد تصمیم‌گیرنده می‌پردازیم. اگر برای مثال، فرد تصمیم‌گیرنده قصد خرید نان داشته باشد، عوامل تاثیرگذار بر تصمیم، کمتر خواهند بود.

در آن‌صورت، تنها دو عامل قیمت و کیفیت نان مورد توجه قرار می‌گیرند. ممکن است در مسائل دیگر، عوامل تاثیرگذار بر تصمیم، متعدد باشند. برای مثال زمانی ‌که یکی از اعضای مجلس مسئله‌ای را مطرح می‌کند، نفع رای‌دهندگان، سابقه خودش، احتمال دوباره رای آوردن و بسیاری از عوامل دیگر را مدنظر قرار می‌‌دهد.

در ابتدا باید به جای واژه عامل از واژه «معیار» (Criterion) استفاده کنیم و توجه داشته باشیم که تصمیم‌گیری با وجود معیار‌های متعدد و متضاد، با استفاده از روش‌های تصمیم‌گیری چندمعیاره انجام می‌شود. در فرایند تصمیم‌گیری، متخصص باید مجموعه‌ای از معیار‌ها را $$C=\left\{c_{1},c_{2},...,c_{m}\right\}$$ که خصوصیات یک هدف خاص به شمار می‌روند، مورد بررسی قرار دهد. این خصوصیات، با درنظر گرفتن یک هدف خاص، یک گزینه ‌را نسبت به گزینه دیگر، به مورد بهتری تبدیل می‌کند.

در مثال بیان‌شده که راجع به مقاصد گردشگری برای تعطیلات بود، مجموعه معیار‌ها مطابق موارد زیر در نظر گرفته می‌شود.

  { آب و هوا ، اماکن دیدنی ، محیط } =  C

که در آن

• $$c_{1}$$: آب‌و‌هوا
• $$c_{2}$$: اماکن دیدنی
• $$c_{3}$$: محیط

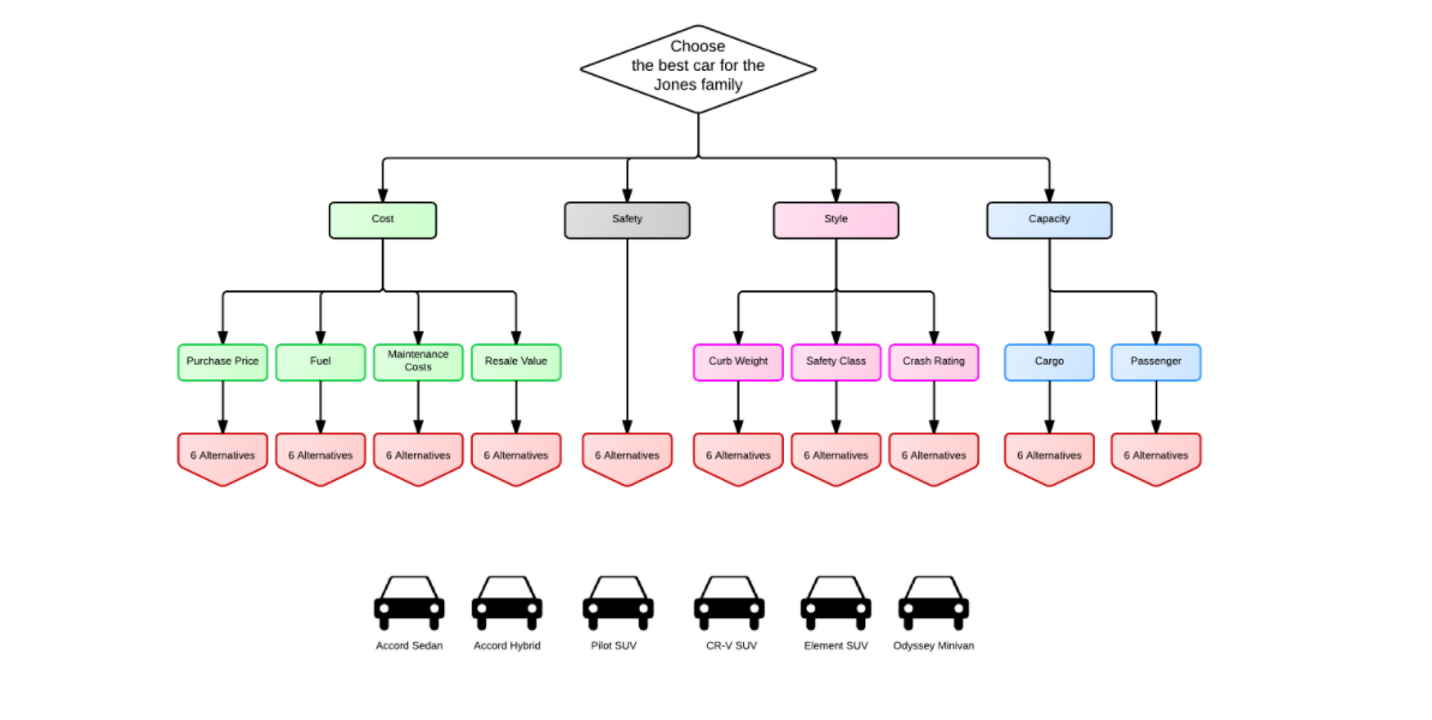
در اینجا به یک شکل رسم شده نیاز داریم که گزینه‌ها، معیار‌ها و هدف را در نظر بگیرد و ساختار مسئله را به شکل بصری نشان دهد. در روش AHP، سلسله مراتب این نقش را به عهده می‌گیرد و به ترتیب از موارد زیر تشکیل شده است.

• هدف
• مجموعه گزینه‌ها
• مجموعه معیارها
• رابطه هدف، معیار و گزینه‌ها

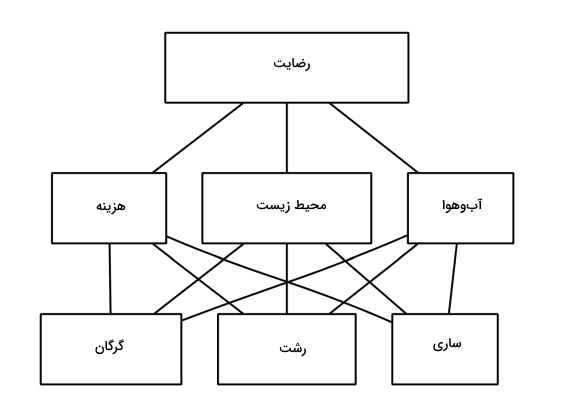
در تصویر بالا سلسله مراتب برای انتخاب شهر شمالی را مشاهده می‌کنید. در بالاترین طبقه، هدف و در پایین‌ترین طبقه، گزینه‌ها قرار دارند. در طبقه میانی می‌توانید معیار‌ها را ملاحظه کنید. خطی که هر دو عنصر را به یکدیگر متصل می‌کند، نشان‌دهنده رابطه وابستگی سلسله مراتبی بین آن‌هاست.

مشکل اصلی ماتریس مقایسه‌ای زوجی $$A$$ در شکل بالا، مقایسه گزینه‌ها بدون درنظر گرفتن معیار است. با پرکردن ماتریس A تصمیم‌گیرنده تنها به رضایت کلی با در نظرگرفتن گزینه‌ها می‌پردازد و هیچ توجهی به معیار‌هایی که به رضایت سراسری می‌انجامد - مانند هزینه، اماکن دیدنی و محیط زیست - ندارد. مانند مثال قبلی، پیچیدگی می‌تواند به صورت یک مشکل بروز کند و راه‌حل، تجزیه مسئله بزرگ‌تر به مسئله کوچک‌تر است.

به همین خاطر، در اینجا، ساعتی پیشنهاد تشکیل ماتریس متفاوتی را به ازای هر معیار ارائه می‌کند. ماتریس $$A^{\left(k\right)}$$، ماتریسی از مقایسه‌های زوجی بین گزینه‌ها طبق معیار K است. ۳ ماتریس «محیط زیست» ( Environment | E)، «اماکن دیدنی» (Sightseeing | S) و «آب‌و‌هوا» (Climate | C) را در نظر بگیرید.

درایه $$a_{13}$$ از ماتریس $$A^{\left(c\right)}$$، نشان‌دهنده این است که تصمیم‌گیرنده در صورت مقایسه آب‌و‌هوای دو شهر، رشت را به ساری ترجیح خواهد داد. ۳ ماتریسی که در ادامه مشاهده می‌شوند به عنوان مثالی از ترجیحات انتخاب شده بوسیله تصمیم‌گیرنده درباره ۳ شهر شمالی با توجه به ۳ معیار گفته‌شده خواهند بود.

$$\mathbf{A}^{(c)}=\left(\begin{array}{ccc} 1 & 1 & 4 \\ 1 & 1 & 4 \\ 1 / 4 & 1 / 4 & 1 \end{array}\right) \quad \mathbf{A}^{(s)}=\left(\begin{array}{ccc} 1 & 2 & 6 \\ 1 / 2 & 1 & 3 \\ 1 / 6 & 1 / 3 & 1 \end{array}\right) \quad \mathbf{A}^{(e)}=\left(\begin{array}{ccc} 1 & 1 / 2 & 1 / 8 \\ 2 & 1 & 1 / 4 \\ 8 & 4 & 1 \end{array}\right)$$

در ادامه، بردار‌های الویت یا وزن‌دهی را تخمین می‌زنیم.

$$\mathbf{w}^{(c)}=\left(\begin{array}{c} 4 / 9 \\ 4 / 9 \\ 1 / 9 \end{array}\right) \quad \mathbf{w}^{(s)}=\left(\begin{array}{l} 6 / 10 \\ 3 / 10 \\ 1 / 10 \end{array}\right) \quad \mathbf{w}^{(e)}=\left(\begin{array}{l} 1 / 11 \\ 2 / 11 \\ 8 / 11 \end{array}\right)$$

حال‌که به جای ۳ بردار، ۱ بردار داریم، تفسیر، حداقل، دو جنبه خواهد داشت. از آن‌جایی که ۳ بردار ۳ بعدی وجود دارند، ممکن است فردی آن‌ها را مانند ۳ نقطه در فضای اقلیدسی ۳ بعدی تصور کند. بردار‌ها، نشان‌دهنده رتبه‌بندی یا وزن‌دهی هستند و می‌توانند با یکدیگر در تضاد باشند. از لحاظ آب‌و‌هوا، گرگان به ساری ترجیح داده می‌شود اما از لحاظ محیط زیست این ترجیح برعکس است.

این منطقی است که فرض کنیم راه حل، از توافق بین ۳ بردار $$W_{e}$$ ، $$W_{c}$$  و  $$W_{s}$$ حاصل می‌شود. با این‌ حال، میانگین حسابی ساده، بهترین راه برای جمع کردن بردار‌ها نیست زیرا به احتمال زیاد، معیار‌ها از میزان اهمیت متفاوتی برخوردار هستند. برای مثال، ممکن است یک مشتری مسن و با توانایی مالی بالا، اهمیت چندانی برای هزینه قائل نشود و تنها به فضایی آرام و دنج برای سپری کردن تعطیلات خود احتیاج داشته باشد.

در این مثال فرضی، معیار محیط زیست مهم‌تر از معیار هزینه خواهد بود. در نتیجه، به نوعی دیگر از تابع میانگین سازی نیاز خواهیم داشت و میانگین حسابی وزنی بکار گرفته خواهد شد. حال، مسئله قابل توجه، یافتن وزن برای اختصاص دادن به بردار‌های متفاوت است.

وزن اختصاص داده شده به هر بردار باید متناسب با اهمیت معیار مربوطه باشد. راه‌حل ارائه‌شده، بکارگیری تکنیک یکسان قبلی است. در ابتدا یک ماتریس مقایسه‌ای زوجی تشکیل می‌شود که اهمیت معیار را با توجه به دسترسی به هدف، مقایسه می‌کند. در مثال گفته شده، ماتریس می‌تواند به صورت زیر باشد.

$$\hat{\mathbf{A}}=\left(\begin{array}{ccc} 1 & 1 / 2 & 1 / 4 \\ 2 & 1 & 1 / 2 \\ 4 & 2 & 1 \end{array}\right)$$

سپس به بردار $$w=\left\{w_{1},w_{2},w_{3}\right\}$$ دست پیدا می‌کنیم که اجزای آن‌را وزن‌های معیار تشکیل می‌دهند.

$$\hat{\mathbf{w}}=\left(\begin{array}{l} 1 / 7 \\ 2 / 7 \\ 4 / 7 \end{array}\right)$$

طبق این بردار، تصمیم‌گیرنده - در مثال ما، خانواده - به معیار سوم یا همان محیط زیست علاقه‌مند است. در ادامه، ترکیب خطی $$w^{\left(e\right)}$$ ، $$w^{\left(c\right)}$$ و  $$w^{\left(s\right)}$$ را بررسی می‌کنیم.

$$\mathbf{w}=\hat{w}_{1} \mathbf{w}^{(c)}+\hat{w}_{2} \mathbf{w}^{(s)}+\hat{w}_{3} \mathbf{w}^{(e)}$$

حال، به رتبه‌بندی نهایی رسیده‌ایم و می‌توانیم بهترین گزینه یا گزینه با بالاترین امتیاز را انتخاب کنیم که همان $$x_{3}$$ در مثال ما یا شهر ساری است. در نهایت، بهترین گزینه، عضوی از مجموعه $$\left\{x_{i}\mid w_{i}\geq w_{j}, \forall i , j\right\}$$ است. نقش وزن معیار را می‌توان با یک مثال عددی نشان داد. بردار اهمیت برای معیار را به‌جای $$\left(1/7,4/7,2/7\right)^{T}$$، $$\left(1/7,2/7,4/7\right)^{T}$$در نظر بگیرید. با این‌کار، اهمیت نهایی به صورت $$\left(0.43,0.29,0.28\right)^{T}$$ خواهد بود و بهترین گزینه حالا، $$x_{1}$$ یا رشت خواهد شد.

\begin{aligned}
=& \frac{1}{7}\left(\begin{array}{l}
4 / 9 \\
4 / 9 \\
1 / 9
\end{array}\right)+\frac{2}{7}\left(\begin{array}{l}
6 / 10 \\
3 / 10 \\
1 / 10
\end{array}\right)+\frac{4}{7}\left(\begin{array}{l}
1 / 11 \\
2 / 11 \\
8 / 11
\end{array}\right) \\
\approx\left(\begin{array}{l}
0.287 \\
0.253 \\
0.460
\end{array}\right)
\end{aligned}

توجه داشته باشید که سلسله مراتب می‌تواند سطوح بیشتری از معیار را در بر بگیرد. برای مثال، برای انتخاب بهترین شهر برای تعطیلات، معیار آب‌و هوا می‌تواند به چندین معیار کوچک‌تر مانند احتمال بارش باران، طول روز و دما تقسیم شود که هرکدام به نحوی به مفهوم آب‌و‌هوا مربوط می‌شوند. در اینجا فضای کافی را برای رسم سلسله مراتبی با معیار‌های متعد نداریم اما در ادامه مثالی را با معیار‌های بیشتر مطرح می‌کنیم.

مثال سلسله مراتب با معیار‌های بیشتر

در این مثال، به صورت فرضی، سلسله مراتب را برای انتخاب اتومبیل، بررسی می‌کنیم. توجه داشته باشید که چرخ، «معیار کوچک‌تری» (Sub Criteria) برای مکانیک و زیبایی اتومبیل، در نظر گرفته می‌شود.

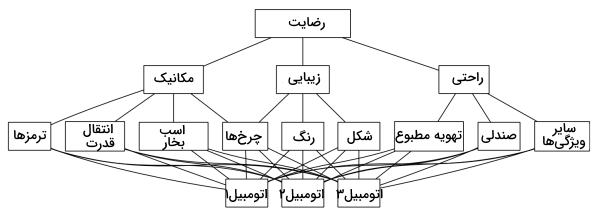
در دنیای واقعی نیز از روش AHP برای انتخاب دستگاه اتومبیل مطلوب استفاده شده است. تا اینجا، با استفاده از مثال‌های ساده، ۳ گام اصلی روش AHP را بررسی کرده‌ایم که به ترتیب در ادامه، شرح داده شده‌اند.

• بررسی ساختار مسئله و مفهوم سلسله مراتب
• استخراج مقایسه‌های زوجی
• بدست آوردن بردار رتبه‌بندی یا وزن و ترکیب‌های خطی آن‌ها

کاربردهای روش AHP در دنیای واقعی

با این ‌وجود، تا به اینجا، موقعیت‌های ساده‌ با فرض‌های متفاوت در نظر گرفته شده‌اند. در ادامه، بکارگیری روش AHP را به عنوان مدلی منعطف‌تر نیز بررسی می‌کنیم. لازم به یادآوری نیست که مثال‌های دنیای واقعی در سطح بالاتری از پیچیدگی قرار دارند.

ارزیابی شهر و برنامه‌ریزی

ساعتی، روش AHP را برای رتبه‌بندی مجموعه‌ای از شهر‌ها از قابل سکونت‌ترین تا غیرقابل سکونت‌ترین بکار برد. او در تحقیقاتش به مجموعه‌ای از شهر‌ها در ایالات متحده آمریکا توجه کرد. درواقع، رضایت از هدف نهایی یا همان قابل سکونت بودن، می‌تواند به رضایت از چندین معیار، برای مثال محیط، خدمات و امنیت تقسیم شود و مجدداً امکان تقسیم هر کدام از این معیار‌ها به معیار‌های کوچک‌تر وجود دارد. برای مثال، بخش خدمات می‌تواند به معیار‌های کوچک‌تری مانند امکانات حمل‌و‌نقل، خدمات درمانی و ... تقسیم شود. بدون شک بعضی از شهر‌ها قابل سکونت‌تر از سایر شهر‌ها خواهند بود.

رتبه‌بندی کشور‌ها

تا اواخر دهه ۱۹۸۰ میلادی، رتبه‌بندی کشور‌ها بر اساس جی دی پی سرانه صورت می‌گرفت یا اینکه مهم‌ترین معیار در نظر گرفته می‌شد. در اوایل دهه ۹۰ میلادی، معیاری جامع و ترکیبی با در نظرگرفتن چندین عامل، توسط اقتصاددانانی مانند «آمارتیاسن» (Amartya Sen) -اقتصاددان هندی - تحت عنوان «شاخص توسعه انسانی»  (Human Development Index | HDI) بوجود آمد.

در سال ۱۹۸۷ میلادی، روش AHP برای رتبه‌بندی کشورها با درنظرگرفتن چند معیار ارائه شد. در این مطالعه، گزینه‌ها، کشور‌ها بودند و معیار شامل تمام ویژگی‌هایی بود که می‌توانست یک کشور را به کشور بهتری تبدیل کند. درواقع، با انتخاب مناسب معیار، این نوع بهره‌گیری از AHP می‌تواند به عنوان اصول اولیه در تحلیل چند متغیره رتبه‌بندی کشور‌ها بکار رود.

خدمات گوشی‌های تلفن همراه

با رایج شدن استفاده از گوشی‌های هوشمند، خدمات تلفن همراه و اپلیکیشن‌های آن‌ها موفق‌تر می‌شوند و به بخشی از زندگی روزانه کاربران آن‌ها تبدیل شده‌اند. یکی از موارد مهم، تشخیص و درک عوامل مهم موفقیتی است که موجب مقبولیت و پذیرش دستگاه‌های تلفن همراه و خدمات متنوع آن‌ها می‌شوند. مدل‌های قدیمی‌تر تنها مجموعه‌ای محدود از عوامل مقبولیت را مورد ملاحظه قرار می‌دهند و بر ارزش‌های قدیمی خدمات تلفن همراه مانند کارایی، استفاده آسان و هزینه تمرکز می‌کنند.

بعضی از محققان، روش AHP را برای تعیین مهم‌ترین معیار تاثیرگذار بر مقبولیت دستگاه‌های تلفن همراه و خدمات آن نزد مشتریان ارائه کرده‌اند. ویژگی‌های اصلی مدنظر قرارگرفته شامل مدل پرداخت، عملکرد، ارزش افزوده، کیفیت و هزینه هستند.

اهدای عضو

به صورت کلی، تعداد افراد نیازمند به عضو‌های اهدا شده بیشتر از کل تعداد اعضای اهدایی است و انواع مختلف تخصیص اعضا می‌تواند پیامد‌های قابل توجهی را به همراه داشته باشد. بعضی از مسائل بهینه‌سازی ترکیبی ارائه شده‌اند تا بتوانند به بهترین نحو ممکن اهداکنندگان و اعضا را با یکدیگر منطبق کنند. بعضی از الگوریتم‌ها این مورد را در نظر می‌گیرند که ممکن است فردی نسبت به سایرین در مدت زمان کوتاه‌تری به عضو اهدا شده احتیاج داشته باشد و زمان مسئله‌ای حیاتی برای او محسوب شود.

در مطالعه‌ای، محققان از روش AHP برای تجزیه ۴ معیار سرعت عمل، کارایی، منفعت و برابری استفاده کردند و در نهایت، اهمیت آن‌ها را در فرایند انطباق اهداکنندگان و اعضا، تخمین زدند. در این نمونه، بیماران همان گزینه‌ها بودند اما تعداد بالای آن‌ها تصمیم‌گیری با بکارگیری نظر شخصی را با دشواری روبه‌رو می‌کرد.

خوشبختانه، در این مسئله، ماتریس‌های مقایسه زوجی، به صورت خودکار پر شده بودند زیرا کمی کردن معیار‌های متفاوت به سادگی صورت می‌پذیرفت. برای مثال، اگر، امید به زندگی دو بیمار ۱ و ۲ سال بود، نتیجه گرفته شده این بود که در آن معیار، شتاب لازم برای انجام عمل برای بیمار اول دو برابر بیمار دوم است.

پیش‌بینی شطرنج

از روش AHP برای پیش‌بینی نیز استفاده شده است. یعنی ورزشکاران، گزینه و خصوصیات آن‌ها، معیار در نظر گرفته می‌شود. همچنین، بازیکن با بالاترین امتیاز را به عنوان محتمل‌ترین برنده می‌شناسیم. در اینجا، به بکارگیری روش AHP در مسابقات شطرنج اشاره می‌کنیم. از AHP برای تعیین نتیجه لیگ قهرمانی جهانی شطرنج در سال میلادی و همچنین مسابقات بین «فیشر» (Fischer) و «اسپاسکی» (Spassky) در سال ۱۹۷۲ میلادی و «کورشنوی» (Korchnoi) و «کارپف» (Karpov) در سال ۱۹۷۸ میلادی استفاده شده است. سلسله مراتب احتمالی برای این مسئله را می‌توانید در شکل زیر مشاهده کنید.

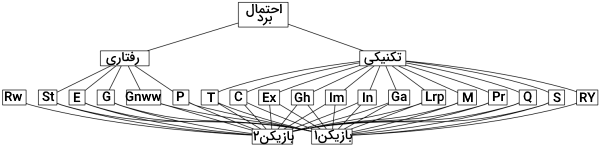
مقادیر وزن‌ها در $$w_{1},...,w_{n}$$ در رابطه با پیش‌بینی می‌تواند به عنوان «احتمال نظری» (Subjective Probability) در نظر گرفته شود. برای مثال، در این مسئله $$w_{1}$$و$$w_{2}$$ می‌توانند به عنوان احتمال نظری برنده شدن دو قهرمان شطرنج به شمار روند.

در تصویر سلسله مراتب بالا می‌توانید احتمال برنده شدن دو بازیکن شطرنج را باتوجه به دو معیار رفتاری و تکنیکی و معیارهای کوچک‌تر مشاهده کنید. از این معیار‌ها می‌توان به (خونسردی و تمایل به برنده شدن) (GN | Good Nerves and Will to Win)، «شخصیت»(Personality | P)، «قدرت بدنی» (Stamina  |  ST)، «غرور» (Ego | E)، «محاسبات» (Calculation | Q)، «تجربه » (Experience | EX)، «سلامت» (Good Health | GH)، «تخیل» (Imagination | IM)، «شهود» (Intuition)، «میزان خشونت در بازی» (Game Aggressiveness | GA)، «برنامه ریزی بلندمدت» (Long Range Planning | LRP)، «حافظه» (Memory  | M)، «آمادگی» (Preparation | PR)، «سرعت عمل» (Quickness | Q)، «جوان بودن» (Relative Youth | RY)، «ثانیه‌ها» (Seconds | S)، «فن بازی» (Technique | M) اشاره کرد.

محدودیت‌های روش AHP چیست؟

روش AHP بدون خطا نیست. کاربران AHP باید از محدودیت‌های آن و مواردی که در آن‌ها استفاده از AHP نادرست است، اطلاع داشته باشند. در اینجا به ۲ مورد از محدودیت‌های این روش اشاره می‌کنیم.

• معکوس شدن مرتبه
• مقیاس‌های متفاوت

معکوس شدن مرتبه

یکی از نقد‌های وارده به AHP، برگرفته از پدیده «معکوس شدن مرتبه» (Rank Reversal) است. از زمان انتشار مقاله «وان نومان» (Von Neumann) و «مورگنسترن» (Morgenstern)، برای متدولوژی‌های تحلیل تصمیم‌گیری به اصولی نیاز بوده است. طبق یکی از این اصول، اگر گزینه جدیدی به مجموعه اصلی گزینه‌ها افزوده شود، رابطه ترتیبی (<) در مجموعه قبلی گزینه‌ها نباید تغییر کند.

با جابجا کردن این مفهوم در زندگی روزانه، اگر فردی در حال انتخاب یک وعده غذایی باشد و آش را به سوپ ترجیح دهد، زمانی که به او ماهی تعارف می‌کنند نباید ترجیحاتش نسبت به آش و سوپ تغییری بکند. «بلتون» (Belton) و همکاران، مثال بعدی را مطرح کردند تا امکان وقوع معکوس شدن رتبه‌بندی را نشان دهند. ماتریس‌های زیر را در نظر بگیرید.

$$\mathbf{A}^{(a)}=\left(\begin{array}{ccc} 1 & 1 / 9 & 1 \\ 9 & 1 & 9 \\ 1 & 1 / 9 & 1 \end{array}\right) \quad \mathbf{A}^{(b)}=\left(\begin{array}{ccc} 1 & 9 & 9 \\ 1 / 9 & 1 & 1 \\ 1 / 9 & 1 & 1 \end{array}\right) \quad \mathbf{A}^{(c)}=\left(\begin{array}{ccc} 1 & 8 / 9 & 8 \\ 9 / 8 & 1 & 9 \\ 1 / 8 & 1 / 9 & 1 \end{array}\right)$$

در این ماتریس‌ها، ۳ گزینه با در نظر گرفتن ۳ معیار با یکدیگر مقایسه می‌شوند. با فرض اینکه هر ۳ معیار، وزن یکسان، برابر ۱/۳ دارند، آخرین بردار وزن‌دهی یا الویت به شکل$$\left(0.45,0.47,0.08\right)^{T}$$ است و گزینه‌ها به صورت $$x_{2}$$ بیشتر از $$x_{1}$$ بیشتر از $$x_{3}$$، رتبه‌بندی شده‌اند. تا اینجا، خطایی وجود ندارد. حال فرض کنید، گزینه جدیدی تحت عنوان $$x_{4}$$ به مجموعه اصلی و اولیه اضافه و ارزیابی‌های جدید مطابق ماتریس‌های زیر باشند.

$$\mathbf{A}^{(a)}=\left(\begin{array}{cccc} 1 & 1 / 9 & 1 & 1 / 9 \\ 9 & 1 & 9 & 1 \\ 1 & 1 / 9 & 1 & 1 / 9 \\ 9 & 1 & 9 & 1 \end{array}\right) \quad \mathbf{A}^{(b)}=\left(\begin{array}{cccc} 1 & 9 & 9 & 9 \\ 1 / 9 & 1 & 1 & 1 \\ 1 / 9 & 1 & 1 & 1 \\ 1 / 9 & 1 & 1 & 1 \end{array}\right) \quad \mathbf{A}^{(c)}=\left(\begin{array}{cccc} 1 & 8 / 9 & 8 & 8 / 9 \\ 9 / 8 & 1 & 9 & 1 \\ 1 / 8 & 1 / 9 & 1 & 1 / 9 \\ 9 / 8 & 1 & 9 & 1 \end{array}\right)$$

توجه داشته باشید که ترجیحات درباره ۳ گزینه اولیه تغییر نکرده است. با این ‌حال، با توجه به مهم‌بودن معیار، بردار وزن‌دهی جدید به شکل $$\left(0.37,0.29,0.06,0.29\right)^{T}$$ خواهد بود و در نتیجه، مرتبه جدید به صورت $$x_{1}$$ بیشتر از $$x_{۲}$$، $$x_{۲}$$ به صورت تقریبی برابر با $$x_{4}$$ و $$x_{4}$$ بیشتر از $$x_{۳}$$ است.

حال، $$x_{۱}$$ ، بالاترین امتیاز را دارد. تاثیر این خطا، زمانی آشکارتر می‌شود که به مثال اولیه یا همان انتخاب شهر شمالی رجوع کنیم. در این‌صورت، با در نظر گرفتن یک شهر دیگر، مانند آمل، ممکن بود ترتیب اصلی ۳ شهر دیگر، بهم بریزد و مشکلات مهم‌تری در دنیای واقعی بوجود بیاید.

مقیاس‌های متفاوت

با وجود برتر بودن نظریه سنجش نسبی، تصمیم‌گیرنده می‌تواند از لحاظ آب‌و‌هوا بیان کند که گرگان ۴ برابر بهتر از ساری است. در زندگی روزمره ، افراد از عبارت‌هایی مانند (من سوپ قارچ را کمی بیشتر از سوپ گوجه ترجیح می‌دهم) یا (من به شدت موز را به سیب ترجیح می‌دهم) استفاده می‌کنند. برای کمک به فرد تصمیم‌گیرنده، بعضی از اصطلاحات زبانی ارائه شده‌اند و برای هرکدام، با توجه به درایه‌های $$a_{ij}$$ ارزش متفاوتی در نظر گرفته شده است.

بنابراین، تصمیم‌گیرنده می‌تواند نظریه‌های خود را درباره جفت‌ها با بکارگیری عبارات زبانی، اظهار کند که در نهایت به اعداد حقیقی تبدیل می‌شوند. مقیاس ساعتی و «مقیاس تعدیل شده» (Balanced Scale) برای کمی کردن عبارات زبانی را می‌توانید در جدول زیر مشاهده کنید.

اینکه کدام یک از این معیار‌ها بهتر هستند هنوز تعیین نشده است اما مقیاس ساعتی بهینه به شمار نمی‌رود. مقیاس تعدیل‌شده زمینه علمی بهتری دارد و باتوجه به آزمایش‌های تجربی انجام شده با افراد، بوجود آمده است. اغلب محققان، عقیده دارند که برای تخصیص دادن اعداد به عبارت‌های کلامی، استفاده از اعداد صحیح ۱ تا ۹ و اعداد معکوس آن‌ها، مناسب خواهد بود. مهم‌ترین دلیل این انتخاب، توانایی محدود انسان‌ها در پردازش اطلاعات است.

بردار الویت یا بردار وزن‌دهی چیست ؟

همان‌طور که مشاهده کردید، یکی از گام‌های مهم در روش AHP، بدست آوردن «بردار الویت» (Priority Vector) برای هر ماتریس مقایسه زوجی است. توجه داشته باشید اگر هرکدام از درایه‌های ماتریس، $$a_{ij}$$ دقیقاً معادل نسبت بین دو وزن $$w_{i}$$ و $$w_{j}$$ باشند، تمام ستون‌های $$A$$ با یکدیگر تناسب خواهند داشت و در نتیجه بردار وزن‌دهی یا الویت، معادل هر بردار نرمال‌سازی شده (بردار یکه) از ماتریس A خواهد بود.

در این‌صورت، تمام اطلاعات قرار داده شده در ماتریس $$A$$ در بردار $$w$$ قرار خواهند داشت و اطلاعات از بین نمی‌روند. زمانی که درایه‌های ماتریس $$A$$ دقیقاً بصورت نسبت‌هایی از وزن‌ها، نباشند، بردار وزنی حاوی اطلاعات ماتریس A، بدست نمی‌آید. از آنجایی‌که، نمی‌توان بدون بردار الویت از روش AHP، استفاده کرد، بوجود آوردن روش‌های هوشمندانه برای تخمین مناسب بردار الویت، ضروری به شمار می‌رود.

واضح است که از روش‌های متفاوت می‌توان، بردار‌های الویت مختلفی را بدست آورد، غیر از زمانی که درایه‌‌های ماتریس، نشان‌دهنده نسبت‌های بین وزن‌ها باشند که در این‌صورت از تمامی روش‌ها به بردار$$w$$ یکسانی، دست می‌یابیم. در «عقلانیت کامل» (Perfect Rationality) بردار $$w$$ بدست آمده از هر روش، به صورت مقابل است $$A=\left(w_{i}/w_{j}\right)_{n\times n}$$.

روش بردار ویژه چیست؟

شناخته‌شده‌ترین روش برای تخمین بردار الویت، به شمار می‌‌رود که توسط خود ساعتی ارايه شده است. طبق این روش، بردار الویت باید برابر با بردار ویژه اصلی (بردار ویژه بدست آمده از بزرگ‌ترین مقدار ویژه) در نظر گرفته شود. در جبر خطی عموماً، این بردار، «پرون-فربنیوس» (Perron-Frobenius) نامیده می‌شود. این روش برگرفته از مشاهداتی است که در ادامه مطرح شده‌اند. ماتریس A را در نظر بگیرید که درایه‌های آن، دقیقاً برابر نسبت بین وزن‌ها هستند، در این صورت مطابق محاسبات زیر با ضرب آن‌ها در بردار $$w$$ به مقدار مشاهده شده دست می‌یابیم.

$$\mathbf{A} \mathbf{w}=\left(\begin{array}{cccc} w_{1} / w_{1} & w_{1} / w_{2} & \ldots & w_{1} / w_{n} \\ w_{2} / w_{1} & w_{2} / w_{2} & \ldots & w_{2} / w_{n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n} / w_{1} & w_{n} / w_{2} & \ldots & w_{n} / w_{n} \end{array}\right)\left(\begin{array}{c} w_{1} \\ \vdots \\ w_{n} \end{array}\right)=\left(\begin{array}{c} n w_{1} \\ \vdots \\ n w_{n} \end{array}\right)=n \mathbf{w}$$

از جبر خطی می‌دانیم که در معادله $$AW=nW$$، مقادیر $$n$$ و $$w$$ به ترتیب برابر یکی از مقادیر ویژه و یکی از بردار‌های ویژه ماتریس A هستند. همچنین، با دانستن اینکه دیگر مقدار ویژه ماتریس A صفر و مرتبه آن برابر N-1 است، درمیابیم که n بزرگ‌ترین مقدار ویژه ماتریس A به شمار می‌رود.

بنابراین، اگر درایه‌های ماتریس A به صورت نسبت‌هایی بین وزن‌ها باشند، بردار وزن، بردار ویژه‌ای از ماتریس A با توجه به مقدار ویژه $$n$$ خواهد بود. ساعتی این نتیجه را با جایگزین کردن $$n$$ با حداکثر مقدار ویژه ماتریس A که جامع‌تر است، به تمام ماتریس‌های مقایسه‌ای زوجی تعمیم می‌دهد.

بنابراین بردار $$w$$ را می‌توان از هر زوج مقایسه‌ای ماتریس A به صورت راه‌حل معادلات زیر بدست آورد.

$$\left\{\begin{array}{l} \mathbf{A} \mathbf{w}=\lambda_{\max } \mathbf{w} \\ \mathbf{w}^{T} \mathbf{1}=1 \end{array}\right.$$

که در آن$$\lambda_{\max}$$ ، حداکثر مقدار ویژه ماتریس A و $$1=(1,...,1)^{T}$$است. با اینکه این مسئله به سادگی توسط نرم‌افزار‌های ریاضی و اکسل قابل حل است اما تفسیر آن برای بعضی از افراد، طاقت‌فرسا به شمار می‌رود.

روش میانگین هندسی چیست؟

روش پرکاربرد دیگر برای تخمین بردار الویت، «روش میانگین هندسی» (Geometric Mean Method) ارائه شده توسط «کرافورد» (Crawford) و «ویلیامز»(Williams) است. طبق این روش، هر عضو تشکیل‌دهنده بردار $$w$$ از تقسیم میانگین هندسی عناصر سطر مربوطه بر جمله نرمال‌سازی بدست می‌آید. در نهایت، مجموع اجزای تشکیل‌دهنده بردار $$w$$، برابر ۱ می‌شوند.

$$w_{i}=\left(\prod_\left(j=1\right)^n a_{ij} \right)^{\frac{1}{n}}\div\sum_i^n\left(\prod_j^na_{ij}\right)^{\frac{1}{n}}$$

مثال تخمین بردار الویت با بکارگیری روش میانگین هندسی

ماتریس زیر را در نظر بگیرید.

$$\mathbf{A}=\left(\begin{array}{cccc} 1 & 1 / 2 & 1 / 4 & 3 \\ 2 & 1 & 1 / 2 & 2 \\ 4 & 2 & 1 & 2 \\ 1 / 3 & 1 / 2 & 1 / 2 & 1 \end{array}\right)$$

در ماتریس نام‌برده با استفاده از نکته گفته شده، بردار $$w$$ به شکل زیر محاسبه می‌شود.

$$w\approx \left(0.119,0.208,0.454,0.219\right)^{T}$$

روش‌های دیگر

روش‌های مختلفی برای محاسبه بردار الویت در متون مربوطه ارائه شده‌اند. از میان تمام این مطالعات انجام شده، بعد از رو‌ش‌های بردار ویژه و میانگین هندسی، روشی که در ادامه شرح می‌دهیم، محبوبیت بیشتری بدست آور‌ده‌ است.

روش حداقل مربعات چیست؟

در «روش حداقل مربعات» (Least Squares Method) بردار الویت با توجه به مسئله بهینه‌یابی زیر بدست می‌آید.

حداقل سازی         $$\sum_\left(i=1\right)^n\sum_\left(j=1\right)^n\left(a_{ij}-\frac{w_{i}}{w_{j}}\right)^{2}$$

نسبت به قید               $$\sum_\left(i=1\right)^n w_{i}=1 $$

مسئله بهینه‌سازی می‌تواند حداقل‌کننده‌هایی نسبی داشته باشد و ممکن است الگوریتم بهینه‌سازی اینجا با مشکل مواجه شود که محققان در مقالاتی مجزا، به این مسئله و راه‌حل‌های آن اشاره کرده‌اند.

سازگاری در ماتریس چیست؟

یک تصمیم‌گیرنده عقلایی کامل، باید قادر باشد جفت ترجیحات خود را به صورت دقیق بیان کند، برای مثال $$a_{ij}=w_{i}/w_{j} \forall i,j$$. در ادامه، پیامد‌های این شرط را بر درایه‌های ماتریس زوج مقایسه‌ای A بررسی می‌کنیم. اگر $$a_{ij}a_{jk}$$ را بنویسیم و شرط $$a_{ij}=w_{i}/w_{j} \forall i,j$$ را اعمال کنیم، به نتایج زیر دست می‌یابیم.

$$a_{ij}a_{jk}=\frac{w_{i}}{w_{j}}\frac{w_{j}}{w_{k}}=\frac{w_{i}}{w_{k}}=a_{ik}$$

بنابراین، اگر تمام درایه‌های ماتریس مقایسه‌ای A، شرط $$a_{ij}=w_{i}/w_{j} \forall i,j$$ را رعایت کنند، شرط زیر نیز برقرار خواهد بود.

$$a_{ik}=a_{ij}a_{jk}\forall i,j,k$$

یعنی هر مقایسه مستقیم $$a_{ik}$$ توسط تمام مقایسه‌های غیرمستقیم $$a_{ij}a_{jk}\forall j$$ تایید می‌شود. اصولاً، یک تصمیم‌گیرنده که بتواند به خوبی مقایسه‌های زوجی سازگار را انجام دهد، خود را نقض نخواهد کرد. ماتریسی با این شرایط، ماتریس «سازگار» (Consistent) نامیده می‌شود.

مثال اول سازگاری در ماتریس

۳ سنگ  $$x_{1}$$ ، $$x_{2}$$ و $$x_{3}$$ را در نظر بگیرید.

اگر تصمیم‌گیرنده بیان کند که $$x_{1}$$ سه‌ برابر سنگین‌تر از $$x_{3}$$ باشد یعنی درایه سیزدهم برابر ۳ ($$a_{13}=3$$) است.

همچنین، سنگینی $$x_{1}$$ دوبرابر $$x_{2}$$ است، یعنی درایه دوازدهم با ۲ ($$a_{12}=2$$) برابری می‌کند.

بعلاوه، $$x_{2}$$ دوبرابر سنگین‌تر از $$x_{3}$$ به شمار می‌رود($$a_{23}=2$$).

در ادامه، تصمیم‌گیرنده خود را نقض می‌کند زیرا مستقیماً اعلام می‌کند که $$a_{13}=3$$ اما به صورت غیرمستقیم نشان می‌دهد که ارزش $$a_{13}$$ باید معادل $$a_{12}a_{23}$$ یا ۴ باشد که برابر ۳ نیست. این استدلال را می‌توان به صورت ماتریس‌های زوجی مقایسه‌ای نشان داد.

مثال دوم سازگاری در ماتریس

مثال دیگری را با وجود دو ماتریس مقایسه‌ای دیگر در نظر بگیرید.

$$\left(\begin{array}{ccc} 1 & 2 & 4 \\ 1 / 2 & 1 & 2 \\ 1 / 4 & 1 / 2 & 1 \end{array}\right) \quad\left(\begin{array}{ccc} 1 & 2 & 1 / 2 \\ 1 / 2 & 1 & 2 \\ 2 & 1 / 2 & 1 \end{array}\right)$$

که برای آن‌ها به ترتیب از دو نمودار زیر استفاده می‌کنیم.

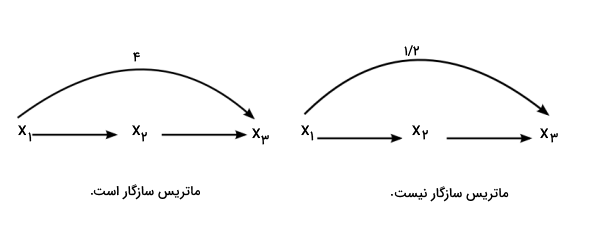
«شاخص عدم سازگاری» (Inconsistency Index)، مانند یک ترمومتر (حرارت سنج) عمل می‌کند. این شاخص، ماتریس‌های مقایسه زوجی را به عنوان داده در نظر می‌گیرد و ناسازگار بودن ارزیابی‌ها را می‌سنجد.

ماتریس‌ها به ندرت سازگار هستند زیرا عوامل بسیاری بر ظهور عدم سازگاری تاثیرگذارند. برای مثال ممکن است از تصمیم‌گیرندگان درخواست شود که از اعداد صحیح و معکوس آن‌ها استفاده کنند. اگر $$3=a_{ij}$$ و $$1/2=a_{ij}$$ باشد، یافتن مقداری سازگار برای $$a_{ik}$$ ناممکن است. همچنین، تعداد انتقال‌پذیری مستقل (i، j و k) در ماتریسی با مرتبه $$n$$ برابر با $$\left(\begin{array}{c}3\\ n\end{array}\right)$$ است که نشان‌دهنده عدم سازگار بودن ماتریس به شمار می‌رود.

شاخص سازگاری چیست ؟

با توجه به در نظرگرفتن ماتریس زوج مقایسه‌ای A، حداکثر مقدار ویژه آن ($$\lambda_{\max}$$) برابر با $$n$$ خواهد بود، اگر و تنها اگر ماتریس سازگاری داشته باشد. ساعتی، «شاخص سازگاری» (Consistency Index) را به شکل زیر ارائه کرد.

$$C I(\mathbf{A})=\frac{\lambda_{\max }-n}{n-1}$$

اگرچه، بررسی‌های عددی نشان‌دهنده این هستند که «ارزش انتظاری» (Expected Value) شاخص سازگاری ماتریسی تصادفی به مرتبه $$n+1$$، به صورت میانگین از ارزش انتظاری ماتریسی تصادفی به مرتبه $$n$$ بزرگ‌تر است. در نتیجه، شاخص سازگاری، ماتریس‌هایی با مراتب متفاوت را به صورت بی‌طرفانه مقایسه نمی‌کند و باید مجدداً، مقیاس‌ٰهای آن بازنگری شوند.

نسبت سازگاری چیست؟

«نسبت سازگاری» (Consistency Ratio)، نسخه بازتنظیم‌شده شاخص سازگاری به شمار می‌رود. ماتریسی با مرتبه $$n$$ را در نظر بگیرید. نسبت سازگاری را می‌توان از تقسیم شاخص سازگاری بر عدد حقیقی $$RI_{n}$$ یا (شاخص تصادفی) بدست آورد. شاخص تصادفی، تخمینی از میانگین شاخص سازگاری بدست آمده از مجموعه‌ای بزرگ از ماتریس‌های تصادفی تولید شده به اندازه $$n$$ است.  بنابراین، نسبت سازگاری به صورت زیر محاسبه می‌شود.

      $$C I(\mathbf{A})=\frac{\lambda_{\max }-n}{n-1}$$

در جدول زیر می‌توانید مقادیر تخمین‌زده شده برای $$RI_{n}$$ را مشاهده کنید. توجه داشته باشید که تولید ماتریس‌های تصادفی به تعریف یک بازه محدود - برای مثال، بازه [۹ و ۱٫۹] - نیاز دارد. به عقیده ساعتی، در عمل، فرد باید ماتریس‌هایی با نسبت سازگاری کمتر مساوی ۰٫۱ را قبول و مقادیر بزرگ‌تر از ۰٫۱ را رد کند. اگر نسبت سازگاری برابر ۰٫۱ باشد به معنی این است که ۱۰ درصد از ارزیابی‌ها، ناسازگار هستند.

مثال شاخص و نسبت سازگاری

ماتریس مقایسه‌ای زوجی زیر را در نظر بگیرید.

$$\mathbf{A}=\left(\begin{array}{cccc} 1 & 2 & 9 & 1 \\ 1 / 2 & 1 & 1 / 3 & 1 / 6 \\ 1 / 9 & 3 & 1 & 2 \\ 1 & 6 & 1 / 2 & 1 \end{array}\right)$$

با محاسبه، حداکثر مقدار ویژه برابر ۵٫۲۸ خواهد بود. با استفاده از فرمول شاخص سازگاری، این مقدار برای ماتریس A معادل ۰٫۴۲۶۶۷ خواهد شد. با تقسیم آن بر $$RI_{4}$$ ، نسبت سازگاری برای ماتریس $$A$$ به صورت تقریبی برابر ۰٫۴۸ بدست می‌آید که بالاتر از حد آستانه ۰٫۱ است. در یک مسئله تصمیم‌گیری، این مورد رایج است که تصمیم‌گیرنده، تا زمان رسیدن نسبت سازگاری به کمتر از ۰٫۱ به تعدیل ارزیابی‌های خود ادامه دهد.

شاخص دترمینان‌ها چیست؟

شاخص دترمینان‌ها توسط «پلائز» (Pelaez) و «لاماتا» (Lamata) بوجود آمده و از ویژگی‌های ماتریسی با مرتبه ۳ است. با بسط دادن دترمینان ماتریس حقیقی ۳ در ۳، دترمینان آن به صورت زیر بدست می‌آید.

$$det(A)=\frac{a_{13}}{a_{12}a_{23}}+\frac{a_{12}a_{23}}{a_{13}}-2$$

اگر ماتریس A، ناسازگار باشد، آنگاه $$a_{13}\neq a_{12}a_{23}$$ و دترمینان ماتریس A، مثبت خواهد بود زیرا به صورت کلی شرایط مقابل برقرار هستند.

$$\frac{a}{b}+\frac{b}{a}-2>0$$

$$\forall a\neq b$$    و $$a,b>0$$.

این امکان وجود دارد که این نتیجه را به ماتریس‌هایی با مراتب بالاتر از ۳ تعمیم دهیم و شاخص عدم سازگاری را به عنوان میانگین دترمینان‌های تمام ماتریس‌های کوچک‌تر $$T_{ijk}$$ بوجود آمده از ماتریسی زوج مقایسه‌ای معین به شرح زیر تعریف کنیم.

$$\mathbf{T}_{i j k}=\left(\begin{array}{ccc} 1 & a_{i j} & a_{i k} \\ a_{j i} & 1 & a_{j k} \\ a_{k i} & a_{k j} & 1 \end{array}\right)$$

$$\forall i$$

تعداد این ماتریس‌های کوچک‌تر معادل است با $$\left(\begin{array}{c}n\\ 3\end{array}\right)=\frac{n!}{3!\left(n-3\right)!}$$. نتیجه شاخص، نشان‌دهنده عدم سازگاری‌های محاسبه شده برای تمام ماتریس‌های کوچک‌تر $$T_{ijk}$$ است. ($$i$$)

$$CI\left(A\right)=\sum_\left(i=1\right)^\left(n-2\right)\sum_\left(j=i+1\right)^\left(n-1\right)\sum_\left(k=j+1\right)^n\left(\frac{a_{ik}}{a_{ij}a_{jk}}+\frac{a_{ij}a_{jk}}{a_{ik}}-2\right)/\left(\begin{array}{c}n\\ 3\end{array}\right)$$

مثال بدست آوردن شاخص سازگاری با بکارگیری دترمینان‌ها

ماتریس A در مثال قبلی را در نظر بگیرید. حال، می‌توانیم میانگین دترمینان‌های ماتریس‌های زیرمجموعه $$T_{ijk}$$ که در آن‌ها $$k$$> $$j$$ و $$i$$ <$$j$$ است را، محاسبه کنیم.

                                                                                  $$=(11.5741+1.3333+16.0556+34.0278)/4=15.7477$$

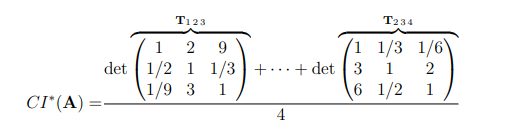
شاخص سازگاری، در تناسب با شاخص عدم سازگاری دیگری به نام $$c_{3}$$ قرار دارد. «ضریب» (Coefficient) $$c_{3}$$ چند جمله‌ای یک ماتریس زوج مقایسه‌ای است که به عنوان شاخص عدم سازگاری توسط «شیرائیشی» (Shiraishi) و «اوباتا» (Obata) ارائه شد. طبق تعریف، چندجمله‌ای ماتریس A، به صورت زیر محاسبه می‌شود.

$$P_{A}\left(\lambda\right)=\lambda^{n}+c_{1}\lambda^{n-1}+...+c_{n-1}\lambda+c_{n}$$

که در آن $$c_{1},...,c_{n}$$ اعداد حقیقی هستند و $$\lambda$$ مجهول به شمار می‌رود. شیرائیشی و همکارانش ثابت کردند که درصورت منفی بودن $$c_{3}$$، ماتریس، به صورت کامل، سازگار نخواهد بود. در حقیقت با توجه به نظریه پرون-فوربنیوس واضح است که  تنها قاعده چندجمله‌ای که منجر به $$\lambda_{max}=n$$ می‌شود، به شرح زیر است.

$$P_{A}\left(\lambda\right)=\lambda^{n-1}\left(\lambda-n\right)$$

در نتیجه، اگر $$c_{3}$$ منفی باشد، با قاعده بالا تناقض خواهد داشت و نشانه مطمئنی از عدم سازگاری است. همچنین، شیرائیشی به همراه همکاران شرح تحلیلی $$c_{3}$$ را به طریق زیر اثبات کرده است.

$$c_{3}=\sum_\left(i=1\right)^\left(n-2\right)\sum_\left(j=i+1\right)^\left(n-1\right)\sum_\left(k=j+1\right)^n\left(2-\frac{a_{ik}}{a_{ij}a_{jk}}-\frac{a_{ij}a_{jk}}{a_{ik}}\right)$$

در فرمول بالا، تناسب میان شاخص سازگاری و $$c_{3}$$ قابل مشاهده‌تر است.

شاخص سازگاری هندسی چیست؟

این شاخص توسط «کرافورد» (Crawford) مطرح شده است. در این شاخص بردار الویت یا بردار وزن‌دهی با روش میانگین هندسی محاسبه می‌شود. با در نظر داشتن این وزن تخمین زده شده، می‌توان میزان نسبی کمی ناسازگاری $$e_{ij}$$ رابرای هر درایه $$a_{ij}$$ به شرح زیر محاسبه کرد.

$$e_{ij}=a_{ij}\frac{w_{j}}{w_{i}}$$

واضح است که برای ماتریس‌های سازگار، ارزش $$e_{ij}$$ برابر با ۱ است زیرا از ضرب درایه در معکوس آن بدست می‌آید.

$$a_{ij}=\frac{w_{i}}{w_{j}}\Rightarrow ln e_{ij}=0$$

حال امکان تعریف شاخص ناسازگاری سراسری وجود دارد. این شاخص از جمع نرمال‌سازی شده موارد نسبی به دست آمده از عدم سازگاری ماتریس A، محاسبه می‌شوند. شاخص ناسازگاری سراسری یا شاخص سازگاری هندسی را می‌توان به شکل زیر محاسبه کرد.

$$GCI(A)=\frac{2}{\left(n-1\right)\left(n-2\right)}\sum_\left(i=1\right)^\left(n-1\right)\sum_\left(j=i+1\right)^n\left(lne_{ij}\right)^{2}$$

مثال شاخص سازگاری هندسی

در اینجا به ماتریس A که پیش‌تر آن‌را معرفی کرده بودیم، رجوع می‌کنیم. با بکارگیری روش میانگین هندسی، بردار الویت یا وزن‌دهی معادل $$w\approx\left(2.06,0,408,0.904,1.316\right)^{T}$$ خواهد شد. در ادامه، راحت‌تر خواهد بود که مقادیر با توجه به فرمول بیان‌شده در بخش شاخص سازگاری هندسی، محاسبه شوند.

$$\mathbf{E}=\left(e_{i j}\right)_{n \times n}=\left(a_{i j} \frac{w_{j}}{w_{i}}\right)_{n \times n}=\left(\begin{array}{cccc} 1 & 0.3964 & 3.9482 & 0.6389 \\ 2.5227 & 1 & 0.7379 & 1.8612 \\ 0.2538 & 1.3554 & 1 & 2.9129 \\ 1.5651 & 1.8612 & 0.3432 & 1 \end{array}\right)$$

در نهایت، با بکارگیری آخرین فرمول بیان شده در شاخص سازگاری هندسی، می‌توان این شاخص را برای ماتریس A محاسبه کرد.

$$GCI\left(A\right)\approx 1.52$$

شاخص سازگاری هارمونیک چیست؟

اگر و تنها اگر، A، ماتریس زوجی مقایسه‌ای سازگاری باشد، ستون‌های آن نسبت‌هایی از یکدیگر هستند و مرتبه ماتریس A برابر ۱ است. در نتیجه، فرض می‌کنیم که هرچه تناسب میان ستون‌ها کمتر باشد، ماتریس سازگاری کمتری دارد. شاخص عدم سازگاری که تنها بر پایه تناسب میان ستون‌های ماتریس بوجود آمده باشد، توسط «استین» (Stein) و «میزی» (Mizzi) ارائه شد.

با در نظر گرفتن ماتریس A، آن‌ها بیان کردند که بردار  فرعی S به صورتی وجود دارد که $$s=\left(s_{1},s_{2},...,s_{n}\right)^{T}$$ و  $$s_{j}=\sum_i^n a_{ij}\forall j$$. ثابت شده بود که $$\sum_j^n s_j^\left(-1\right)=1$$

$$HM\left(s\right)=\frac{n}{\sum_\left(j=1\right)^n \frac{1}{s_{j}}}$$

تابع $$HM$$ خود می‌تواند شاخصی از عدم سازگاری باشد اما طبق تجارب محاسباتی، نرمال‌سازی برای تنظیم رفتار تابع $$HM$$ با شاخص سازگاری انجام شده است. بنابراین «شاخص سازگاری هارمونیک» (Harmonic Consistency Index) به شکل زیر محاسبه می‌شود.

$$HCI\left(A\right)=\frac{\left(HM\left(s\right)-n\right)\left(n+1\right)}{n\left(n-1\right)}$$

مثال شاخص سازگاری هارمونیک

با در نظر گرفتن ماتریس $$A$$، بردار $$s$$به شکل زیر محاسبه می‌شود.

$$s=(\frac{47}{18},12,\frac{65}{6},\frac{25}{6})^{T}$$

میانگین هارمونیک نیز به روش زیر بدست می‌آید.

$$HM\left(s\right)=\frac{4}{\frac{1}{\frac{47}{18}}+\frac{1}{12}+\frac{1}{\frac{65}{6}}+\frac{1}{\frac{25}{6}}}=\frac{733200}{146387}=5.00864$$

حال، امکان بدست آوردن مقدار شاخص سازگاری هارمونیک با قرار دادن مقدار $$HM(s)$$ در فرمول شاخص سازگاری هارمونیک وجود دارد و $$HCI(A)$$ به صورت تقریبی برابر ۰٫۴۲ خواهد بود.

فیلم آموزش فرایند تحلیل سلسله مراتبی AHP در تصمیم‌گیری چند شاخصه

برای یادگیری بیشتر پیرامون روش AHP می‌توانید به آموزش بالا مراجعه کنید. این دوره آموزشی در ۶۹ دقیقه توسط فرادرس تدوین شده است. در ویدئو آموزشی حاضر به ترتیب سرفصل‌های روش AHP، اصول فرایند سلسله مراتبی، ماتریس مقایسات زوجی، مراحل روش AHP و مثال کاربردی در نرم‌افزار Expert Choice بررسی می‌شوند.

• برای مشاهده فیلم آموزش فرایند تحلیل سلسله مراتبی AHP در تصمیم‌گیری چند شاخصه + اینجا کلیک کنید.

سخن پایانی

‌AHP یکی از روش‌هایی است که از زمان بوجود آمدن تا به‌حال، کاربرد‌های زیادی در علوم مختلف داشته است و از روش‌های آسان به شمار می‌رود. با وجود سهولت بکارگیری روش AHP، در مورد مفاهیم زیرمجموعه و روش محاسبه برخی از موارد - با وجود گذشتن چندین سال - همچنان مباحثه وجود دارد.

در این نوشتار آموختیم که روش AHP از ۳ گام، تشخیص مسئله، استخراج ماتریس‌های مقایسه‌ای زوجی و بدست آوردن بردار‌های وزن‌دهی و ترکیب خطی آن‌ها تشکیل شده است. علاوه بر روش‌های مطرح‌شده در این نوشتار، راه‌های متعدد دیگری برای حل مسئله‌ها با روش AHP وجود دارد. از این راه‌های متعدد می‌توان به تنوع روش‌های محاسباتی برای بدست آوردن بردار الویت و شاخص‌های ناسازگاری اشاره کرد.

در AHP، برخلاف سایر زمینه‌ها در ریاضی کاربردی و مدلسازی ریاضی، بسیاری از راه‌ها و شاخص‌ها به‌گونه‌ای ابتکاری و ذهنی مطرح شده‌اند و این مورد موجب شده در این زمینه، مطالب متعددی بوجود بیاید. بهتر است که در آینده روش‌های جدید معرفی‌ شده برای AHP مورد بررسی و مطالعات بیشتری قرار گیرند و همزمان با مطرح شدن آن‌ها شواهد نشان‌دهنده کارایی و اصالت‌شان، ارائه شود.

«مجله فرادرس» در زمینه بورس و تحلیل تکنیکال نیز مطالب جامعی را به زبان ساده تهیه کرده است که در صورت علاقه، می‌توانید به آن‌ها مراجعه کنید.

• اوراق بهادار چیست؟ — به زبان ساده (+ فیلم آموزش رایگان)
• سهام چیست و سهامدار کیست؟ — به زبان ساده
• بورس چیست — به زبان ساده (+ فیلم آموزش رایگان بورس)
• آموزش بورس رایگان | گام به گام برای همه | به زبان ساده
• تفاوت بورس و فرابورس چیست؟ — به زبان ساده
• فرابورس چیست ؟ — به زبان ساده
• بازار پایه چیست؟ | به زبان ساده (+ فیلم آموزش رایگان)
• بورس کالا چیست؟ | به زبان ساده (+ فیلم آموزش رایگان)
• بهترین کارگزاری بورس | بررسی جامع کارگزاری ها
• عرضه اولیه در بورس چیست ؟ | به زبان ساده (+ فیلم آموزش رایگان) 
• صندوق سرمایه گذاری چیست؟ — به زبان ساده
• ETF چیست ؟ (صندوق قابل معامله) | به زبان ساده (+ فیلم آموزش رایگان)
• ارزش خالص دارایی یا NAV چیست ؟ | به زبان ساده
• کد بورسی چیست — راهنمای دریافت کد بورسی — گام به گام
• ثبت نام در بورس و سامانه سجام — راهنمای گام به گام (+ فیلم آموزش رایگان)
• سامانه سجام چیست؟ — راهنمای گام به گام تصویری و ساده
• سبد سهام یا پرتفوی چیست؟ | به زبان ساده
• شاخص بورس چیست؟ | به زبان ساده (+ فیلم آموزش رایگان)
• نمودار بورس و کاربردهای آن — از صفر تا صد (+ فیلم آموزش رایگان)
• سیگنال بورس چیست؟ — به زبان ساده
• حجم مبنا چیست | به زبان ساده (+ فیلم آموزش رایگان)
• سهام شناور چیست؟ — به زبان ساده (+ فیلم آموزش رایگان)
• تحلیل فاندامنتال چیست؟ | به زبان ساده — از صفر تا صد
• تحلیل بنیادی چیست؟ | به زبان ساده
• EPS چیست ؟ — به زبان ساده
• نسبت P/E چیست؟ — به زبان ساده
• پول هوشمند در بورس چیست؟ — به زبان ساده
• آموزش تابلو خوانی بورس | به زبان ساده (+ فیلم آموزش رایگان)
• نوسان گیری در بورس | به زبان ساده (+ فیلم آموزش رایگان)
• افزایش سرمایه در بورس | به زبان ساده (+ فیلم آموزش رایگان)
• پرایس‌اکشن (Price Action) چیست؟ | به زبان ساده و گام به گام
• پولبک (Pull Back) در بورس چیست ؟ — انواع و کاربرد به زبان ساده
• تحلیل تکنیکال بورس ایران | راهنمای کاربردی
• آموزش تحلیل‌ تکنیکال‌‌ بورس رایگان (+ دانلود فیلم آموزش رایگان)
• اندیکاتور CCI چیست؟ — به زبان ساده
• اندیکاتور atr — آموزش به زبان ساده و گام به گام
• امواج الیوت در تحلیل‌ تکنیکال‌‌ | به زبان ساده (+ فیلم آموزش رایگان)
• آموزش فیبوناچی در تحلیل‌ تکنیکال‌‌ بورس‌ | به زبان ساده (+ فیلم آموزش رایگان)
• آموزش اندیکاتور های تحلیل‌ تکنیکال‌‌ بورس | به زبان ساده (+ فیلم آموزش رایگان)
• اندیکاتور استوکاستیک (stochastic) — آموزش کاربردی و به زبان ساده
• معاملات الگوریتمی چیست؟ | به زبان ساده (+ فیلم آموزش رایگان)
• روانشناسی در بورس | راهنمای کاربردی (+ فیلم آموزش رایگان)
• بورس نزدک (NASDAQ)‌ چیست؟ | آنچه باید بدانید به زبان ساده
• ایچیموکو چیست؟ — آموزش اندیکاتور ایچیموکو به زبان ساده
• فارابیکسو — آموزش فارابیکسو کارگزاری فارابی | گام به گام
• خرید سهام در بورس در بورس — آموزش خرید سهام در بورس — گام به گام
• تعدیل در بورس چیست ؟ | به زبان ساده
• DPS در بورس چیست ؟ | مفهوم DPS به زبان ساده
• اندیکاتور MACD چیست ؟ — آموزش تصویری و به زبان ساده