در آموزشهای قبلی از مجموعه مطالب ریاضی مجله فرادرس، انحنا و شعاع انحنا را معرفی کردیم. در این آموزش، با گسترنده منحنی آشنا میشویم.
گسترنده منحنی
منحنی مسطح γ \gamma γ
r = r ( s ) , \large \mathbf { r } = \mathbf { r } \left ( s \right ) , r = r ( s ) ,
که در آن، پارامتر s s s طول قوس منحنی را نشان میدهد. فرض کنید در هر نقطه، خمیدگی منحنی مخالف صفر باشد (K ( s ) ≠ 0 K\left( s \right) \ne 0 K ( s ) = 0 M M M
R = R ( s ) = 1 K ( s ) . \large R = R \left ( s \right ) = \frac { 1 } { { K \left ( s \right ) } } . R = R ( s ) = K ( s ) 1 .
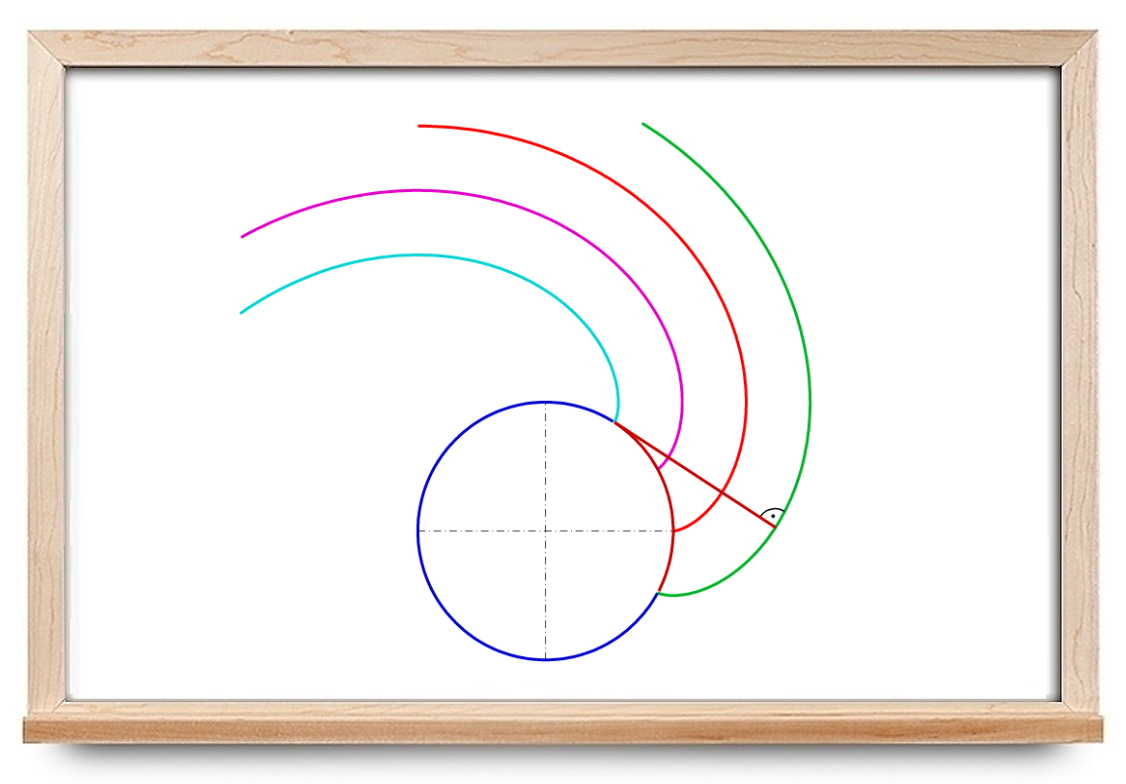
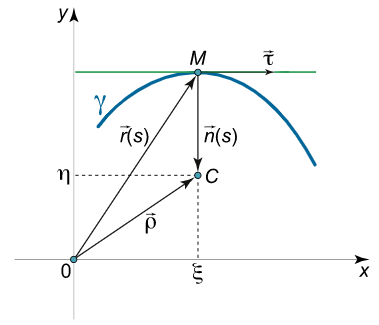
روی خط عمود n \mathbf{n} n M C \mathbf{MC} MC R ( s ) R ( s ) R ( s ) M M M
شکل ۱ نقطه C C C γ \gamma γ M M M
اگر بردار شعاع مرکز خمیدگی را با ρ \boldsymbol{\rho} ρ
ρ = O M + M C = r + R n . \large \boldsymbol { \rho } = \mathbf { O M } + \mathbf { M C } = \mathbf { r } + R \mathbf { n } . ρ = OM + MC = r + R n .
بردار عمود n \mathbf {n} n
n = 1 K d τ d s = 1 K d 2 r d s 2 = R d 2 r d s 2 , \large { \mathbf { n } = \frac { 1 } { K } \frac { { d \boldsymbol { \tau } } } { { d s } } } = { \frac { 1 }{ K } \frac { { { d ^ 2 } \mathbf { r } } } { { d { s ^ 2 } } } } = { R \frac { { { d ^ 2 } \mathbf { r } } } { { d { s ^ 2 } } } , } n = K 1 d s d τ = K 1 d s 2 d 2 r = R d s 2 d 2 r ,
که در آن، τ \boldsymbol\tau τ M M M
ρ = r + R n = r + R 2 d 2 r d s 2 . \large { \boldsymbol \rho = \mathbf { r } + R \mathbf { n } } = { \mathbf { r } + { R ^ 2 } \frac { { { d ^ 2 } \mathbf { r } } } { { d { s ^ 2 } } } . } ρ = r + R n = r + R 2 d s 2 d 2 r .
برای هر نقطه از منحنی، با فرض K ≠ 0 K \ne 0 K = 0 γ \gamma γ
اگر منحنی γ 1 \gamma _ 1 γ 1 γ \gamma γ γ \gamma γ γ 1 \gamma _ 1 γ 1
مرکز خمیدگی را با نقطه C C C ( ξ , η ) \left( {\xi ,\eta } \right) ( ξ , η ) γ \gamma γ
x = x ( t ) , y = y ( t ) , α ≤ t ≤ β , \large { x = x \left ( t \right ) , } \; \; \; { y = y \left ( t \right ) , } \; \; \; \kern-0.3pt { \alpha \le t \le \beta , } x = x ( t ) , y = y ( t ) , α ≤ t ≤ β ,
مختصات مراکز خمیدگی ( ξ , η ) \left( {\xi ,\eta } \right) ( ξ , η )
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ , η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ . \large { \xi = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } , } \; \; \; \kern-0.3pt { \eta = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } . } ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 , η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 .
این فرمولها از عبارت بردار شعاعی ρ \boldsymbol\rho ρ
اگر منحنی γ \gamma γ y = f ( x ) y = f\left( x \right) y = f ( x )
ξ = x – 1 + ( y ’ ) 2 y ′ ′ y ’ , η = y + 1 + ( y ’ ) 2 y ′ ′ . \large { \xi = x – \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } } { { y ^ { \prime \prime } } } y’ , } \; \; \; \kern-0.3pt { \eta = y + \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } }{ { y ^ { \prime \prime } } } . } ξ = x – y ′′ 1 + ( y ’ ) 2 y ’ , η = y + y ′′ 1 + ( y ’ ) 2 .
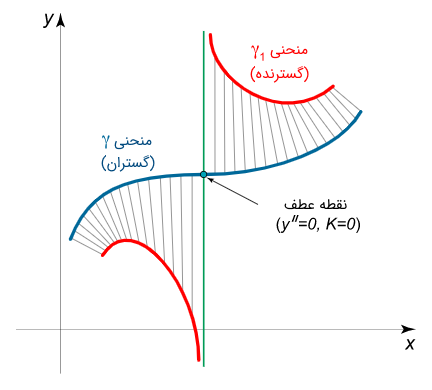
توجه کنید که شرایط خمیدگی غیرصفر در همه نقاط منحنی به اندازه کافی قوی است. در نتیجه، منحنیهای مشخص، برای مثال آنهایی که دارای نقاط عطف هستند، خارج از تحلیلاند. بنابراین، یک مورد عمومیتر خمیدگی دلخواه را بررسی میکنیم. اگر خمیدگی در یک نقطه برابر با صفر باشد، گسترنده در این نقطه دارای یک ناپیوستگی است. این مورد در شکل ۲ نشان داده شده است.
شکل ۲ مثالهای گسترنده منحنی
در این بخش، مثالهای متنوعی از گسترنده منحنی را بررسی خواهیم کرد.
مثال اول گسترنده منحنی
گسترده دایره زیر را تعیین کنید.
x 2 + y 2 = R 2 . \large { x ^ 2 } + { y ^ 2 } = { R ^2 } . x 2 + y 2 = R 2 .
حل: معادله دایره را به فرم پارامتری زیر مینویسیم:
x = R cos t , y = R sin t . \large x = R \cos t , \; \; \; y = R \sin t . x = R cos t , y = R sin t .
مشتقات x x x y y y t t t
x ’ = ( R cos t ) ′ = – R sin t , y = ( R sin t ) ′ = R cos t , \large \begin {align*} x’ & = { \left ( { R \cos t } \right ) ^ \prime } = – R \sin t , \; \; \; \kern-0.3pt y = { \left ( { R \sin t } \right ) ^ \prime } = R \cos t , \end {align*} x ’ = ( R cos t ) ′ = – R sin t , y = ( R sin t ) ′ = R cos t ,
x ′ ′ = ( – R sin t ) ′ = – R cos t , y ′ ′ = ( R cos t ) ′ = – R sin t . \large \begin {align*} { x ^ { \prime \prime } = { \left ( { – R \sin t } \right ) ^ \prime } = – R \cos t , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { R \cos t } \right ) ^ \prime } = – R \sin t . } \end {align*} x ′′ = ( – R sin t ) ′ = – R cos t , y ′′ = ( R cos t ) ′ = – R sin t .
مختصات مرکز خمیدگی ( ξ , η ) \left( {\xi ,\eta } \right) ( ξ , η )
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ , η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ . \large { \xi = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } , } \; \; \; \kern-0.3pt { \eta = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } . } ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 , η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 .
با قرار دادن x x x y y y
$$ \large \require{cancel} \begin {align*} \xi & = x – y’ \frac { { { { \left ( {x’} \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } = { { R \cos t – R \cos t \cdot } \kern0pt { \frac { \cancel { { { R ^ 2 }{ { \sin } ^ 2 } t + { R ^ 2 } { { \cos } ^ 2 } t } } } { \cancel { { { R ^ 2 } { { \sin } ^ 2 } t + { R ^ 2 } { { \cos } ^ 2 } t } } } } } \\ & = { \cancel { R \cos t } – \cancel { R \cos t } \equiv 0;} \end {align*} $$
$$ \large \require {cancel} \begin {align*}<br />
\eta & = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } = { { R \sin t – R \sin t } \cdot \kern0pt { \frac { \cancel { { { R ^ 2 } { { \sin } ^ 2 } t + { R ^ 2 } { { \cos } ^ 2 } t } } } { \cancel { { { R ^ 2 } { { \sin } ^ 2 } t + { R ^ 2 } { { \cos } ^ 2 } t } } } } } \\ & = { R \sin t – R \sin t \equiv 0.}<br />
\end {align*} $$
بنابراین، به یک نتیجه بدیهی میرسیم: گسترنده منحنی دایره تنها یک نقطه (مرکز دایره) است.
مثال دوم گسترنده منحنی
اوولوت بیضی زیر را محاسبه کنید:
x 2 a 2 + y 2 b 2 = 1. \large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 . a 2 x 2 + b 2 y 2 = 1.
حل: فرم پارامتری معادله بیضی به صورت زیر است:
x = a cos t , y = b sin t . \large x = a \cos t , \; \; \; y = b \sin t . x = a cos t , y = b sin t .
مشتقات x x x y y y t t t
x ’ = ( a cos t ) ′ = – a sin t , y ’ = ( b sin t ) ′ = b cos t , \large { x’ = { \left ( { a \cos t } \right ) ^ \prime } = – a \sin t , } \; \; \; \kern-0.3pt { y’ = { \left ( { b \sin t } \right ) ^ \prime } = b \cos t , } x ’ = ( a cos t ) ′ = – a sin t , y ’ = ( b sin t ) ′ = b cos t ,
x ′ ′ = ( – a sin t ) ′ = – a cos t , y ′ ′ = ( b cos t ) ′ = – b sin t . \large { x ^ { \prime \prime } = { \left ( { – a \sin t } \right ) ^ \prime } = – a \cos t , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { b \cos t } \right ) ^ \prime } = – b \sin t . } x ′′ = ( – a sin t ) ′ = – a cos t , y ′′ = ( b cos t ) ′ = – b sin t .
برای محاسبه مختصات مرکز خمیدگی ( ξ , η ) \left( {\xi ,\eta } \right) ( ξ , η )
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ , η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ . \large { \xi = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y^ { \prime \prime } – x ^ { \prime \prime } y’ } } , } \; \; \; \kern-0.3pt { \eta = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } . } ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 , η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 .
با قرار دادن عبارات x x x y y y
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = a cos t – b cos t ⋅ a 2 sin 2 t + b 2 cos 2 t a b sin 2 t + a b cos 2 t = a cos t – cos t ⋅ a 2 sin 2 t + b 2 cos 2 t a = a 2 cos t – a 2 sin 2 t cos t – b 2 cos 3 t a = a 2 cos t ( 1 – sin 2 t ) – b 2 cos 3 t a = 1 a ( a 2 cos 3 t – b 2 cos 3 t ) = a 2 – b 2 a cos 3 t ; \large \begin {align*} \xi & = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } = { { a \cos t – b \cos t } \cdot \kern0pt { \frac { { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 }{ { \cos } ^ 2 } t } } { { a b \, { { \sin } ^ 2 } t + a b \, { { \cos } ^ 2 } t } } } } \\ & = { { a \cos t – \cos t } \cdot \kern0pt { \frac { { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 }{ { \cos } ^ 2 } t } } { a } } } \\ &= { \frac { { { a ^ 2 } \cos t – { a ^ 2 } { { \sin } ^ 2 } t \cos t – { b ^ 2 } { { \cos } ^ 3 } t } } { a } = \frac { { { a ^ 2 } \cos t \left ( { 1 – { { \sin } ^ 2 } t } \right ) – { b ^ 2 } { { \cos } ^ 3 } t } } { a } } \\ & = { \frac { 1 } { a } \left ( { { a ^ 2 } { { \cos } ^ 3 } t – { b ^ 2 } { { \cos } ^ 3 } t } \right ) = \frac { { { a ^ 2 } – { b ^ 2 } } } { a } { \cos ^ 3 } t ; } \end {align*} ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = a cos t – b cos t ⋅ ab sin 2 t + ab cos 2 t a 2 sin 2 t + b 2 cos 2 t = a cos t – cos t ⋅ a a 2 sin 2 t + b 2 cos 2 t = a a 2 cos t – a 2 sin 2 t cos t – b 2 cos 3 t = a a 2 cos t ( 1– sin 2 t ) – b 2 cos 3 t = a 1 ( a 2 cos 3 t – b 2 cos 3 t ) = a a 2 – b 2 cos 3 t ;
η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = b sin t – a sin t ⋅ a 2 sin 2 t + b 2 cos 2 t a b sin 2 t + a b cos 2 t = b sin t – sin t ⋅ a 2 sin 2 t + b 2 cos 2 t b = b 2 sin t – a 2 sin 3 t – b 2 cos 2 t sin t b = b 2 sin t ( 1 – cos 2 t ) – a 2 sin 3 t b = 1 b ( b 2 sin 3 t – a 2 sin 3 t ) = b 2 – a 2 b sin 3 t . \large \begin {align*} \eta & = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } }{ { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } = { { b \sin t – a \sin t } \cdot \kern0pt{ \frac { { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } } { { a b \, { { \sin } ^ 2 } t + a b \, { { \cos } ^ 2 } t } } } } \\ & = { { b \sin t – \sin t } \cdot\kern0pt { \frac { { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } } { b } } } \\ & = { \frac { { { b ^ 2 } \sin t – { a ^ 2 } { \sin ^ 3 } t – { b ^ 2 } { \cos ^ 2 } t \sin t } } { b } } \\ & = { \frac { { { b ^ 2 } \sin t \left ( { 1 – { { \cos } ^ 2 } t } \right ) – { a ^ 2 } { \sin ^ 3 } t } } { b } } \\ & = { \frac { 1 } { b } \left ( { { b ^ 2 } { \sin ^ 3 } t – { a ^ 2 } { \sin ^ 3 } t } \right ) = \frac { { { b ^ 2 } – { a ^ 2 } } } { b } { \sin ^ 3 } t .} \end {align*} η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = b sin t – a sin t ⋅ ab sin 2 t + ab cos 2 t a 2 sin 2 t + b 2 cos 2 t = b sin t – sin t ⋅ b a 2 sin 2 t + b 2 cos 2 t = b b 2 sin t – a 2 sin 3 t – b 2 cos 2 t sin t = b b 2 sin t ( 1– cos 2 t ) – a 2 sin 3 t = b 1 ( b 2 sin 3 t – a 2 sin 3 t ) = b b 2 – a 2 sin 3 t .
در نتیجه، گسترنده منحنی یک بیضی با معادلات پارامتری زیر توصیف میشود:
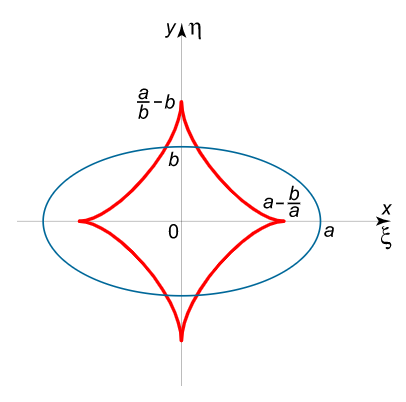
ξ = a 2 – b 2 a cos 3 t = ( a – b a ) cos 3 t , η = b 2 – a 2 b sin 3 t = ( b – a b ) sin 3 t . \large \begin {align*} \xi & = \frac { { { a ^ 2 } – { b ^ 2 } } } { a } { \cos ^ 3 } t = \left ( { a – \frac {b } { a } } \right ) { \cos ^ 3 } t , \; \; \; \kern-0.3pt \\ \eta & = \frac { { { b ^ 2 } – { a ^ 2 } } } { b } { \sin ^ 3 } t = \left ( { b – \frac { a } { b } } \right ) { \sin ^ 3 } t . \end {align*} ξ η = a a 2 – b 2 cos 3 t = ( a – a b ) cos 3 t , = b b 2 – a 2 sin 3 t = ( b – b a ) sin 3 t .
با حذف پارامتر t t t
ξ = a 2 – b 2 a cos 3 t , ⇒ a ξ = ( a 2 – b 2 ) cos 3 t , ⇒ a ξ a 2 – b 2 = cos 3 t , ⇒ ( a ξ ) 2 3 ( a 2 – b 2 ) 2 3 = cos 2 t ; \large \begin {align*} \xi & = \frac { { { a ^ 2 } – { b ^ 2 } } } { a }{ \cos ^ 3 } t , \; \; \Rightarrow { a \xi = \left ( { { a ^ 2 } – { b ^ 2 } } \right ) { \cos ^ 3 } t , } \; \; \\ & \Rightarrow { \frac { { a \xi } }{ { { a ^ 2 } – { b ^ 2 } } } = { \cos ^ 3 } t , } \; \; \Rightarrow { \frac { { { { \left ( { a \xi } \right ) } ^ { \large \frac { 2 }{ 3 } \normalsize } } } } { { { { \left ( { { a ^ 2 } – { b ^ 2 } } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } } = { \cos ^ 2 } t ; } \end {align*} ξ = a a 2 – b 2 cos 3 t , ⇒ a ξ = ( a 2 – b 2 ) cos 3 t , ⇒ a 2 – b 2 a ξ = cos 3 t , ⇒ ( a 2 – b 2 ) 3 2 ( a ξ ) 3 2 = cos 2 t ;
η = b 2 – a 2 b sin 3 t , ⇒ b η = ( b 2 – a 2 ) sin 3 t , ⇒ b η [ – ( a 2 – b 2 ) ] = sin 3 t , ⇒ ( b η ) 2 3 ( a 2 – b 2 ) 2 3 = sin 2 t . \large \begin {align*} \eta & = \frac { { { b ^ 2 } – { a ^ 2 } } } { b }{ \sin ^ 3 } t , \; \; \Rightarrow { b \eta = \left ( { { b ^ 2 } – { a ^ 2 } } \right ) { \sin ^ 3 } t , } \; \; \\ & \Rightarrow { \frac { { b \eta } }{ { \left [ { – \left ( { { a ^ 2 } – { b ^ 2 } } \right ) } \right ] } } = { \sin ^ 3 } t , } \; \;\Rightarrow { \frac { { { { \left ( { b \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } }{ { { { \left ( { { a ^ 2 } – { b ^ 2 } } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } } = { \sin ^ 2 } t . } \end {align*} η = b b 2 – a 2 sin 3 t , ⇒ b η = ( b 2 – a 2 ) sin 3 t , ⇒ [ – ( a 2 – b 2 ) ] b η = sin 3 t , ⇒ ( a 2 – b 2 ) 3 2 ( b η ) 3 2 = sin 2 t .
با جمع مجذور سینوس و کسینوس، خواهیم داشت:
( a ξ ) 2 3 ( a 2 – b 2 ) 2 3 + ( b η ) 2 3 ( a 2 – b 2 ) 2 3 = 1 , ⇒ ( a ξ ) 2 3 + ( b η ) 2 3 = ( a 2 – b 2 ) 2 3 . \large { \frac { { { { \left ( { a \xi } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } } { { { { \left ( { { a ^ 2 } – { b ^ 2 } } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } } + \frac { { {{ \left ( { b \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } }{ { { { \left ( { { a ^ 2 } – { b ^ 2 } } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } } = 1 , } \; \; \Rightarrow { { \left ( { a \xi } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } + { \left ( { b \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } = { \left ( { { a ^ 2 } – { b ^ 2 } } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } . } ( a 2 – b 2 ) 3 2 ( a ξ ) 3 2 + ( a 2 – b 2 ) 3 2 ( b η ) 3 2 = 1 , ⇒ ( a ξ ) 3 2 + ( b η ) 3 2 = ( a 2 – b 2 ) 3 2 .
سه تساوی a ξ = X a\xi = X a ξ = X b η = Y b\eta = Y b η = Y a 2 – b 2 = A {a^2} – {b^2} = A a 2 – b 2 = A
X 2 3 + Y 2 3 = A 2 3 . \large { X ^ { \large \frac { 2 } { 3 } \normalsize } } + { Y ^ { \large \frac { 2 } { 3 } \normalsize } } = { A ^ { \large \frac { 2 } { 3 } \normalsize } } . X 3 2 + Y 3 2 = A 3 2 .
همانطور که میبینیم، گسترنده منحنی بیضی یک منحنی ستارهگون است. شکل ۳ این منحنی را نشان میدهد.
شکل ۳ مثال سوم گسترنده منحنی
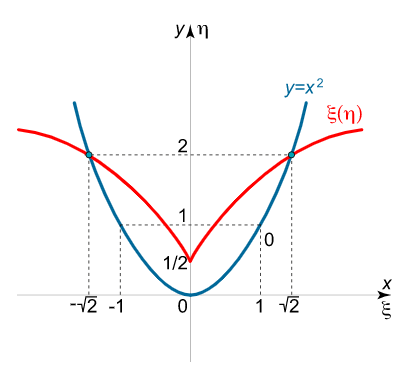
گسترنده منحنی سهمی y = x 2 y = x ^ 2 y = x 2
حل: برای یک منحنی داده شده با یک معادله ضمنی، مختصات مرکز خمیدگی با فرمولهای زیر تعیین میشود:
ξ = x – 1 + ( y ’ ) 2 y ′ ′ y ’ , η = y + 1 + ( y ’ ) 2 y ′ ′ . \large { \xi = x – \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } } { { y ^ { \prime \prime } } } y’ , } \; \; \; \kern-0.3pt { \eta = y + \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } }{ { y ^ { \prime \prime } } } . } ξ = x – y ′′ 1 + ( y ’ ) 2 y ’ , η = y + y ′′ 1 + ( y ’ ) 2 .
با جایگذاری تابع داده شده، خواهیم داشت:
ξ = x – 1 + ( y ’ ) 2 y ′ ′ y ’ = x – 1 + ( 2 x ) 2 2 ⋅ 2 x = x – x ( 1 + 4 x 2 ) = – 4 x 3 ; \large \begin {align*} \xi & = x – \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } }{ { y ^ { \prime \prime } } } y’ = { x – \frac { { 1 + { { \left ( { 2 x } \right ) } ^ 2 } } } { 2 } \cdot 2 x } \\ & = { x – x \left ( { 1 + 4 { x ^ 2 } } \right ) } = { – 4 { x ^ 3 } ; } \end {align*} ξ = x – y ′′ 1 + ( y ’ ) 2 y ’ = x – 2 1 + ( 2 x ) 2 ⋅ 2 x = x – x ( 1 + 4 x 2 ) = –4 x 3 ;
η = y + 1 + ( y ’ ) 2 y ′ ′ = x 2 + 1 + ( 2 x ) 2 2 = x 2 + 1 + 4 x 2 2 = 3 x 2 + 1 2 . \large \begin {align*} \eta & = y + \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } }{ { y ^ { \prime \prime } } } = { { x ^ 2 } + \frac { { 1 + { { \left ( { 2 x } \right ) } ^ 2 } } } { 2 } }\\ & = { { x ^ 2 } + \frac { { 1 + 4 { x ^ 2 } } } { 2 } } = { 3 { x ^ 2 } + \frac { 1 } { 2 } . } \end {align*} η = y + y ′′ 1 + ( y ’ ) 2 = x 2 + 2 1 + ( 2 x ) 2 = x 2 + 2 1 + 4 x 2 = 3 x 2 + 2 1 .
با حذف متغیر x x x ξ ( η ) \xi \left( \eta \right) ξ ( η )
η = 3 x 2 + 1 2 , ⇒ η – 1 2 = 3 x 2 , ⇒ x 2 = η 3 – 1 6 , ⇒ x = ± ( η 3 – 1 6 ) 1 2 . \large \begin {align*} \eta & = 3 { x ^ 2 } + \frac { 1 } { 2 } , \; \; \Rightarrow { \eta – \frac { 1 } { 2 } = 3 { x ^ 2 } , \; \; } \\ & \Rightarrow { { x ^ 2 } = \frac { \eta } { 3 } – \frac { 1 } {6 } , \; \; } \Rightarrow { x = \pm { \left ( { \frac { \eta } { 3 } – \frac { 1 } { 6 } } \right ) ^ { \large \frac { 1 } { 2 } \normalsize } } . } \end {align*} η = 3 x 2 + 2 1 , ⇒ η – 2 1 = 3 x 2 , ⇒ x 2 = 3 η – 6 1 , ⇒ x = ± ( 3 η – 6 1 ) 2 1 .
در نتیجه، داریم:
ξ = – 4 x 3 = – 4 ⋅ [ ± ( η 3 – 1 6 ) 1 2 ] 3 = ± 4 ( η 3 – 1 6 ) 3 2 , \large { \xi = – 4 { x ^ 3 } = – 4 \cdot { \left [ { \pm { { \left ( { \frac { \eta } { 3 } – \frac { 1 } { 6 } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } \right ] ^ 3 } } = { \pm 4 { \left ( { \frac { \eta } { 3 } – \frac { 1 } { 6 } } \right ) ^ { \large \frac { 3 } { 2 } \normalsize } } , } ξ = –4 x 3 = –4 ⋅ ± ( 3 η – 6 1 ) 2 1 3 = ± 4 ( 3 η – 6 1 ) 2 3 ,
که در آن، η ≥ 1 2 \eta \ge \large\frac{1}{2}\normalsize η ≥ 2 1
سهمی و گسترنده آن در شکل ۴ رسم شدهاند.
شکل ۴ گسترنده منحنی بالا شبیه یک دمچلچلهای است که معادله آن یک سهمی شبهمکعبی است.
مثال چهارم گسترنده منحنی
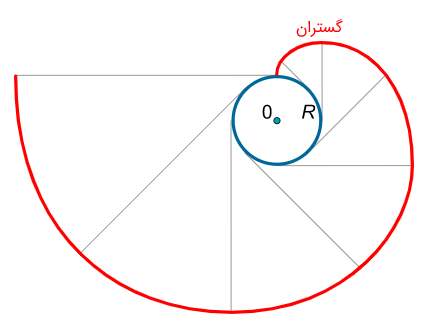
گسترنده مارپیچ لگاریتمی r = e θ r = e ^ \theta r = e θ
حل: منحنی در دستگاه مختصات کارتزین با دستگاه معادلات زیر بیان میشود:
x = r cos θ = e θ cos θ , y = r sin θ = e θ sin θ . \large { x = r \cos \theta = { e ^ \theta } \cos \theta ,} \; \; \; \kern-0pt { y = r \sin \theta = { e ^ \theta } \sin \theta . } x = r cos θ = e θ cos θ , y = r sin θ = e θ sin θ .
این توصیف معادله منحنی به فرم پارامتری است که در آن، زاویه θ \theta θ
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ , η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ . \large { \xi = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } , } \; \; \; \kern-0.3pt { \eta = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } . } ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 , η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 .
مشتقها به صورت زیر هستند:
$$ \large \begin {align*}<br />
\require {cancel} { x’ = { \left ( { { e ^ \theta } \cos \theta } \right ) ^ \prime } } = { { e ^ \theta } \cos \theta – { e ^ \theta } \sin \theta } = { { e ^ \theta } \left ( { \cos \theta – \sin \theta } \right ) ; }<br />
\end {align*} $$
x ′ ′ = [ e θ ( cos θ – sin θ ) ] ′ = e θ ( cos θ – sin θ ) + e θ ( – sin θ – cos θ ) = e θ ( cos θ – sin θ − sin θ – cos θ ) = – 2 e θ sin θ ; \large \begin {align*} x ^ { \prime \prime } & = \left [ { { e ^ \theta } \left ( { \cos \theta – \sin \theta } \right ) } \right ] ^ \prime = { { e ^ \theta } \left ( { \cos \theta – \sin \theta } \right ) + { e ^ \theta } \left ( { – \sin \theta – \cos \theta } \right ) } \\ & = { { e ^ \theta } \left ( { \cancel { \cos \theta } – \sin \theta } \right . } -{ \left . { \sin \theta – \cancel { \cos \theta } } \right ) } = { – 2 { e ^ \theta } \sin \theta ; } \end {align*} x ′′ = [ e θ ( cos θ – sin θ ) ] ′ = e θ ( cos θ – sin θ ) + e θ ( – sin θ – cos θ ) = e θ ( cos θ – sin θ − sin θ – cos θ ) = –2 e θ sin θ ;
y ’ = ( e θ sin θ ) ′ = e θ sin θ + e θ cos θ = e θ ( sin θ + cos θ ) ; \large { y’ = { \left ( { { e ^ \theta } \sin \theta } \right ) ^ \prime } } = { { e ^ \theta } \sin \theta + { e ^ \theta } \cos \theta } = { { e ^ \theta } \left ( { \sin \theta + \cos \theta } \right ) ; } y ’ = ( e θ sin θ ) ′ = e θ sin θ + e θ cos θ = e θ ( sin θ + cos θ ) ;
y ′ ′ = [ e θ ( sin θ + cos θ ) ] ′ = e θ ( sin θ + cos θ ) + e θ ( cos θ – sin θ ) = e θ ( sin θ + cos θ + cos θ – sin θ ) = 2 e θ cos θ . \large \begin {align*} y ^ { \prime \prime } & = \left[ { { e ^ \theta } \left ( { \sin \theta + \cos \theta } \right ) } \right ] ^ \prime = { { e ^ \theta } \left ( { \sin \theta + \cos \theta } \right) + { e ^ \theta } \left ( { \cos \theta – \sin \theta } \right ) } \\ & = { { e ^ \theta } \left ( { \cancel { \sin \theta } + \cos \theta } \right . } + { \left .{ \cos \theta – \cancel { \sin \theta } } \right ) } = { 2 { e ^ \theta } \cos \theta . } \end {align*} y ′′ = [ e θ ( sin θ + cos θ ) ] ′ = e θ ( sin θ + cos θ ) + e θ ( cos θ – sin θ ) = e θ ( sin θ + cos θ + cos θ – sin θ ) = 2 e θ cos θ .
عبارات ξ \xi ξ η \eta η
F = ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = 1 2 ⋅ 2 1 = 1. \large { F = \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } } = { \frac { 1 } { 2 } \cdot \frac { 2 } { 1 } = 1 . } F = x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = 2 1 ⋅ 1 2 = 1.
در نتیجه، مختصات ξ \xi ξ η \eta η
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = x – y ’ F = e θ cos θ – e θ ( sin θ + cos θ ) = – e θ sin θ = – y ; \large \begin {align*} \xi & = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } = { x – y’ F } \\ & = { { e ^ \theta } \cos \theta – { e ^ \theta } \left ( { \sin \theta + \cos \theta } \right ) } = { – { e ^ \theta } \sin \theta = – y ; } \end {align*} ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = x – y ’ F = e θ cos θ – e θ ( sin θ + cos θ ) = – e θ sin θ = – y ;
η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = y + x ’ F = e θ sin θ + e θ ( cos θ – sin θ ) = e θ cos θ = x . \large \begin {align*} \eta & = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } = { y + x’ F } \\ & = { { e ^ \theta } \sin \theta + { e ^ \theta } \left ( { \cos \theta – \sin \theta } \right ) } = { { e ^ \theta } \cos \theta = x . } \end {align*} η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = y + x ’ F = e θ sin θ + e θ ( cos θ – sin θ ) = e θ cos θ = x .
بنابراین، اگر دستگاه مختصات اولیه x O y {xOy} x O y π 2 \large\frac{\pi }{2}\normalsize 2 π ξ O η {\xi O \eta} ξ O η − y - y − y ξ \xi ξ x x x η \eta η r = e θ r = e ^ \theta r = e θ π 2 \large\frac{\pi }{2}\normalsize 2 π
مثال پنجم گسترنده منحنی
گسترنده منحنی چرخزاد زیر را به دست آورید:
x = t – sin t , y = 1 – cos t . \large { x = t – \sin t , } \; \; \; \kern-0.3pt { y = 1 – \cos t . } x = t – sin t , y = 1– cos t .
حل: ابتدا مشتق منحنی داده شده را به دست میآوریم:
x ’ = ( t – sin t ) ′ = 1 – cos t , y ’ = ( 1 – cos t ) ′ = sin t . \large { x’ = { \left ( { t – \sin t } \right ) ^ \prime } = 1 – \cos t , } \; \; \; \kern-0.3pt { y’ = { \left ( { 1 – \cos t } \right ) ^ \prime } = \sin t . } x ’ = ( t – sin t ) ′ = 1– cos t , y ’ = ( 1– cos t ) ′ = sin t .
x ′ ′ = ( 1 – cos t ) ′ = sin t , y ′ ′ = ( sin t ) ′ = cos t . \large { x ^ { \prime \prime } = { \left ( { 1 – \cos t } \right ) ^ \prime } = \sin t , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { \sin t } \right)^\prime } = \cos t.} x ′′ = ( 1– cos t ) ′ = sin t , y ′′ = ( sin t ) ′ = cos t .
مختصات مرکز خمیدگی به صورت زیر است:
( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = ( 1 – cos t ) 2 + sin 2 t ( 1 – cos t ) cos t – sin t sin t = 1 – 2 cos t + cos 2 t + sin 2 t cos t – cos 2 t – sin 2 t = 2 ( 1 – cos t ) cos t – 1 = – 2 ; \large \begin {align*} \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } & = { \frac { { { { \left ( { 1 – \cos t } \right ) } ^ 2 } + { { \sin } ^ 2 } t } } { { \left ( { 1 – \cos t } \right ) \cos t – \sin t \sin t } } } \\ & = { \frac { { 1 – 2 \cos t + { { \cos } ^ 2 } t + { { \sin } ^ 2 } t } } { { \cos t – { { \cos } ^ 2 } t – { { \sin } ^ 2 } t } } } \\ & = { \frac { { 2 \left ( { 1 – \cos t } \right ) } } { { \cos t – 1 } } = – 2 ; } \end {align*} x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = ( 1– cos t ) cos t – sin t sin t ( 1– cos t ) 2 + sin 2 t = cos t – cos 2 t – sin 2 t 1–2 cos t + cos 2 t + sin 2 t = cos t –1 2 ( 1– cos t ) = –2 ;
ξ = x – y ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = t – sin t – sin t ⋅ ( – 2 ) = t + sin t ; \large { \xi = x – y’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } } = { t – \sin t – \sin t \cdot \left ( { – 2 } \right)} = {t + \sin t;} ξ = x – y ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = t – sin t – sin t ⋅ ( –2 ) = t + sin t ;
η = y + x ’ ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = 1 – cos t + ( 1 – cos t ) ⋅ ( – 2 ) = cos t – 1. \large { \eta = y + x’ \frac { { { { \left ( { x’ } \right ) } ^ 2 } + { { \left ( { y’ } \right ) } ^ 2 } } } { { x’ y ^ { \prime \prime } – x ^ { \prime \prime } y’ } } } = { 1 – \cos t + \left ( { 1 – \cos t } \right ) \cdot \left ( { – 2 } \right ) } = { \cos t – 1 . } η = y + x ’ x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = 1– cos t + ( 1– cos t ) ⋅ ( –2 ) = cos t –1.
در ادامه، پارامتر t t t t = τ + π t = \tau + \pi t = τ + π τ \tau τ π \pi π t t t
حال مختصات مرکز خمیدگی ξ \xi ξ η \eta η τ \tau τ
ξ = t + sin t = τ + π + sin ( τ + π ) = [ τ – sin τ ] + π ; \large { \xi = t + \sin t } = { \tau + \pi + \sin \left ( { \tau + \pi } \right ) } = { \left [ { \tau – \sin \tau } \right ] + \pi ; } ξ = t + sin t = τ + π + sin ( τ + π ) = [ τ – sin τ ] + π ;
η = cos t – 1 = cos ( τ + π ) – 1 = – cos τ + 1 – 2 = [ 1 – cos τ ] – 2. \large { \eta = \cos t – 1 } = { \cos \left ( { \tau + \pi } \right ) – 1 } = { – \cos \tau + 1 – 2 } = { \left [ { 1 – \cos \tau } \right ] – 2 . } η = cos t –1 = cos ( τ + π ) –1 = – cos τ + 1–2 = [ 1– cos τ ] –2.
بنابراین، گسترنده منحنی چرخزاد نیز یک چرخزاد است. موقعیت آن نسبت به منحنی اولیه با بردار ( π , – 2 ) \left( {\pi , – 2} \right) ( π , –2 ) t → τ t \to \tau t → τ
مثال ششم گسترنده منحنی
ثابت کنید منحنی با معادلاتِ
x = R ( cos t + t sin t ) , y = R ( sin t – t cos t ) \large { x = R \left ( { \cos t + t \sin t } \right ) , } \; \; \; \kern-0.3pt { y = R \left ( { \sin t – t \cos t } \right ) } x = R ( cos t + t sin t ) , y = R ( sin t – t cos t )
گسترنده منحنی دایرهای با شعاع R R R
حل: مشتقات x x x y y y t t t
$$ \large \begin {align*} \require {cancel}<br />
x’ & = {\left[ {R\left( {\cos t + t\sin t} \right)} \right]^\prime } = {R\left( { – \cancel{\sin t} + \cancel{\sin t} + t\cos t} \right) = Rt\cos t,} \\<br />
x^{\prime\prime} & = {\left( {Rt\cos t} \right)^\prime } ={ R\left( {\cos t – t\sin t} \right),} \\<br />
y’ &= {\left[ {R\left( {\sin t – t\cos t} \right)} \right]^\prime } = {R\left( {\cancel{\cos t} – \cancel{\cos t} + t\sin t} \right) = Rt\sin t,} \\<br />
y^{\prime\prime} & = {\left( {Rt\sin t} \right)^\prime } = {R\left( {\sin t + t\cos t} \right).}<br />
\end {align*} $$
اکنون مختصات مرکز خمیدگی منحنی را محاسبه میکنیم:
D = ( x ’ ) 2 + ( y ’ ) 2 x ’ y ′ ′ – x ′ ′ y ’ = 1. \large {D = \frac{{{{\left( {x’} \right)}^2} + {{\left( {y’} \right)}^2}}}{{x’y^{\prime \prime} – x^{\prime\prime}y’}} } = { 1.} D = x ’ y ′′ – x ′′ y ’ ( x ’ ) 2 + ( y ’ ) 2 = 1.
در نتیجه، مختصات مرکز به صورت زیر خواهد بود:
$$ \large \require {cancel} \begin {align*} \xi = x – y’ D & = { R \left ( { \cos t + t \sin t } \right ) – R t \sin t \cdot 1 } \\ & = { R \cos t + \cancel { R t \sin t } – \cancel { R t \sin t } } = { R \cos t ; } \end {align*} $$
$$ \large \require {cancel} \begin {align*}<br />
{ \eta = y + x’ D } & = { R \left ( { \sin t – t \cos t } \right ) + R t \sin t \cdot 1 } \\ & = { R \sin t – \cancel { R t \cos t } + \cancel { R t \cos t } } = { R \sin t . }<br />
\end {align*} $$
معادلات پارامتری گسترنده منحنی دایره به شعاع R R R
ξ = R cos t , η = R sin t . \large \xi = R \cos t , \; \; \; \eta = R \sin t . ξ = R cos t , η = R sin t .
در مختصات کارتزین ( ξ , η ) \left( {\xi ,\eta } \right) ( ξ , η )
ξ 2 + η 2 = R 2 . \large { \xi ^ 2 } + { \eta ^ 2 } = { R ^ 2 } . ξ 2 + η 2 = R 2 .
گستران دایره به صورت یک مارپیچ است (شکل ۵).
شکل ۵ مثال هفتم گسترنده منحنی
معادله گسترنده هذلولوی y = 1 x y = \large\frac{1}{x}\normalsize y = x 1
حل: مشتقات اول و دوم تابع هذلولوی به صورت زیر هستند:
y ’ = ( 1 x ) ′ = – 1 x 2 , y ′ ′ = ( – 1 x 2 ) ′ = 2 x 3 . \large { y’ = { \left ( { \frac { 1 } { x } } \right ) ^ \prime } = – \frac { 1 } { { { x ^ 2 } } } , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) ^ \prime } = \frac { 2 } { { { x ^ 3 } } } . } y ’ = ( x 1 ) ′ = – x 2 1 , y ′′ = ( – x 2 1 ) ′ = x 3 2 .
در نتیجه، مختصات مرکز خمیدگی هذلولوی به صورت زیر خواهد بود:
ξ = x – 1 + ( y ’ ) 2 y ′ ′ y ’ = x – 1 + ( – 1 x 2 ) 2 2 x 3 ⋅ ( – 1 x 2 ) = x – 1 + 1 x 4 2 x 3 ⋅ ( – 1 x 2 ) = x + ( x 4 + 1 ) x 3 2 x 4 x 2 = x + x 4 + 1 2 x 3 = 2 x 4 + x 4 + 1 2 x 3 = 3 x 4 + 1 2 x 3 ; \large \begin {align*} \xi & = x – \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } } { { y ^ { \prime \prime } } } y’ = { x – \frac { { 1 + { { \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } ^ 2 } } } { { \frac { 2 } { { { x ^ 3 } } } } } \cdot \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } \\ & = { x – \frac { { 1 + \frac { 1 } { { { x ^ 4 }} } } } { { \frac { 2 } { { {x ^ 3 } } } } } \cdot \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } = { x + \frac { { \left ( { { x ^ 4 } + 1 } \right ) { x ^ 3 } } } { { 2 { x ^ 4 } { x ^2 } } } } \\ & = { x + \frac { { { x ^ 4 } + 1 } } { { 2 { x ^ 3 } }} } = { \frac { { 2 { x ^ 4 } + { x ^ 4 } + 1 } } { { 2 { x ^ 3 } } } } = { \frac { { 3 { x ^ 4 } + 1 } } { { 2 { x ^ 3 } } } ; } \end {align*} ξ = x – y ′′ 1 + ( y ’ ) 2 y ’ = x – x 3 2 1 + ( – x 2 1 ) 2 ⋅ ( – x 2 1 ) = x – x 3 2 1 + x 4 1 ⋅ ( – x 2 1 ) = x + 2 x 4 x 2 ( x 4 + 1 ) x 3 = x + 2 x 3 x 4 + 1 = 2 x 3 2 x 4 + x 4 + 1 = 2 x 3 3 x 4 + 1 ;
η = y + 1 + ( y ’ ) 2 y ′ ′ = 1 x + 1 + ( – 1 x 2 ) 2 2 x 3 = 1 x + 1 + 1 x 4 2 x 3 = 1 x + ( x 4 + 1 ) x 3 2 x 4 = 1 x + x 4 + 1 2 x = x 4 + 3 2 x . \large \begin {align*} \eta & = y + \frac { { 1 + { { \left ( { y’ } \right ) } ^ 2 } } } { { y ^ { \prime \prime } } } = { \frac { 1 } { x } + \frac { { 1 + { { \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } ^ 2 } } } { { \frac { 2 } { { { x ^ 3 } } } } } } \\ & = { \frac { 1 } { x } + \frac {{ 1 + \frac { 1 } { { { x ^ 4 } } } } } { { \frac { 2 }{ { { x ^ 3 } } } } } } = { \frac { 1 } { x } + \frac { { \left ( { { x ^ 4 } + 1 } \right ) { x ^ 3 } } } { { 2 { x ^ 4 } } } } \\ & = { \frac { 1 } { x } + \frac { { { x ^ 4} + 1 } } { { 2 x } } } = { \frac { { { x ^ 4 } + 3 } } { { 2 x } } .} \end {align*} η = y + y ′′ 1 + ( y ’ ) 2 = x 1 + x 3 2 1 + ( – x 2 1 ) 2 = x 1 + x 3 2 1 + x 4 1 = x 1 + 2 x 4 ( x 4 + 1 ) x 3 = x 1 + 2 x x 4 + 1 = 2 x x 4 + 3 .
با استفاده از عملیات جبری، متغیر x x x ξ \xi ξ η \eta η ξ \xi ξ η \eta η
ξ + η = 3 x 4 + 1 2 x 3 + x 4 + 3 2 x = 3 x 4 + 1 + x 6 + 3 x 2 2 x 3 = x 6 + 3 x 4 + 3 x 2 + 1 2 x 3 = ( x 2 + 1 ) 3 2 x 3 = 1 2 ( x 2 + 1 x ) 3 = 1 2 ( x + 1 x ) 3 ; \large \begin {align*} { \xi + \eta } & = { \frac { { 3 { x ^ 4 } + 1 } } { { 2 { x ^3 } } } + \frac { { { x ^ 4 } + 3 } } { { 2 x } } } = { \frac { { 3 { x ^ 4 } + 1 + { x ^ 6 } + 3 { x ^ 2 } } } { { 2 { x ^ 3 } } } } \\ & = { \frac { { { x ^ 6 } + 3 { x ^4 } + 3 { x ^ 2 } + 1 } }{ { 2 { x ^ 3 } } } } = { \frac { { { { \left ( { { x ^ 2 } + 1 } \right ) } ^ 3 } } } { { 2 { x ^ 3 } } } } \\ & = { \frac { 1 } { 2 } { \left ( { \frac { { { x ^ 2 } + 1 } } { x } } \right ) ^ 3 } } = { \frac { 1 } { 2 } { \left ( { x + \frac { 1 } { x } } \right ) ^ 3 } ; } \end {align*} ξ + η = 2 x 3 3 x 4 + 1 + 2 x x 4 + 3 = 2 x 3 3 x 4 + 1 + x 6 + 3 x 2 = 2 x 3 x 6 + 3 x 4 + 3 x 2 + 1 = 2 x 3 ( x 2 + 1 ) 3 = 2 1 ( x x 2 + 1 ) 3 = 2 1 ( x + x 1 ) 3 ;
ξ – η = 3 x 4 + 1 2 x 3 – x 4 + 3 2 x = 3 x 4 + 1 – x 6 – 3 x 2 2 x 3 = – x 6 – 3 x 4 + 3 x 2 – 1 2 x 3 = – ( x 2 – 1 ) 3 2 x 3 = – 1 2 ( x 2 – 1 x ) 3 = – 1 2 ( x – 1 x ) 3 . \large \begin {align*} { \xi – \eta } & = { \frac { { 3 { x ^ 4 } + 1 } } { { 2 { x ^ 3 } } } – \frac { { { x ^ 4 } + 3 } } { { 2 x } } } = { \frac { { 3 { x ^ 4 } + 1 – { x ^ 6 } – 3 { x ^ 2 } } } { { 2 { x ^ 3 } } } } \\ & = { – \frac { { { x ^ 6 } – 3 { x ^ 4 } + 3 { x ^ 2 } – 1 } } { { 2 { x ^ 3 } } } } = { – \frac { { { { \left ( { { x ^ 2 } – 1 } \right ) } ^ 3 } }} { { 2 { x ^3 } } } } \\ & = { – \frac { 1 } { 2 } { \left ( { \frac { { { x ^ 2 } – 1 } } { x } } \right ) ^ 3 } } = { – \frac { 1 } { 2 } { \left ( { x – \frac { 1 } { x } } \right ) ^ 3 } . } \end {align*} ξ – η = 2 x 3 3 x 4 + 1 – 2 x x 4 + 3 = 2 x 3 3 x 4 + 1– x 6 –3 x 2 = – 2 x 3 x 6 –3 x 4 + 3 x 2 –1 = – 2 x 3 ( x 2 –1 ) 3 = – 2 1 ( x x 2 –1 ) 3 = – 2 1 ( x – x 1 ) 3 .
با اعمال جذر مکعب، روابط زیر به دست میآیند:
( ξ + η ) 1 3 = 1 2 3 ( x + 1 x ) , ( ξ – η ) 1 3 = – 1 2 3 ( x – 1 x ) . \large { { \left ( { \xi + \eta } \right ) ^ { \large \frac { 1 }{ 3 } \normalsize } } = \frac { 1 } { { \sqrt [ \large 3 \normalsize ]{ 2 } } } \left ( { x + \frac { 1 } { x } } \right ) , } \; \; \; \kern-0.3pt { { \left ( { \xi – \eta } \right ) ^ { \large \frac { 1 }{ 3 } \normalsize } } = – \frac { 1 } { { \sqrt [ \large 3 \normalsize ]{ 2 } } } \left ( { x – \frac { 1 } { x } } \right ) . } ( ξ + η ) 3 1 = 3 2 1 ( x + x 1 ) , ( ξ – η ) 3 1 = – 3 2 1 ( x – x 1 ) .
اکنون هر معادله را به توان دو میرسانیم:
( ξ + η ) 2 3 = 1 4 3 ( x + 1 x ) 2 = 1 4 3 ( x 2 + 2 + 1 x 2 ) , \large { { \left ( { \xi + \eta } \right ) ^ { \large \frac { 2 }{ 3 } \normalsize } } } = { \frac { 1 } { { \sqrt [ \large 3 \normalsize]{ 4 } } } { \left ( { x + \frac { 1 } { x } } \right ) ^ 2 } } = { \frac { 1 } { { \sqrt [ \large 3 \normalsize ] { 4 } } } \left ( { { x ^ 2 } + 2 + \frac { 1 } { { { x ^ 2 } } } } \right ) , } ( ξ + η ) 3 2 = 3 4 1 ( x + x 1 ) 2 = 3 4 1 ( x 2 + 2 + x 2 1 ) ,
( ξ – η ) 2 3 = 1 4 3 ( x – 1 x ) 2 = 1 4 3 ( x 2 – 2 + 1 x 2 ) . \large { { \left ( { \xi – \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } } = { \frac { 1 } { { \sqrt [ \large 3 \normalsize ] { 4 } } } { \left ( { x – \frac { 1 } { x } } \right ) ^ 2 } } = { \frac { 1 } { { \sqrt [ \large 3 \normalsize ] { 4 } } } \left ( { { x ^ 2 } – 2 + \frac { 1 } { { { x ^ 2 } } } } \right ) . } ( ξ – η ) 3 2 = 3 4 1 ( x – x 1 ) 2 = 3 4 1 ( x 2 –2 + x 2 1 ) .
4 3 ( ξ + η ) 2 3 = x 2 + 2 + 1 x 2 , 4 3 ( ξ – η ) 2 3 = x 2 – 2 + 1 x 2 \large { \sqrt [ \large 3 \normalsize ] { 4 } { \left ( { \xi + \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } = { x ^ 2 } + 2 + \frac { 1 } { { { x ^ 2 } } } , } \; \; \; \kern-0.3pt { \sqrt [ \large 3 \normalsize ] { 4 } { \left ( { \xi – \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } = { x ^ 2 } – 2 + \frac { 1 } { { { x ^ 2 } } } } 3 4 ( ξ + η ) 3 2 = x 2 + 2 + x 2 1 , 3 4 ( ξ – η ) 3 2 = x 2 –2 + x 2 1
و معادله دوم را از معادله اول کم میکنیم:
4 3 [ ( ξ + η ) 2 3 – ( ξ – η ) 2 3 ] = x 2 + 2 + 1 x 2 – ( x 2 – 2 + 1 x 2 ) , ⇒ 4 3 [ ( ξ + η ) 2 3 – ( ξ – η ) 2 3 ] = 4 , ⇒ 4 3 [ ( ξ + η ) 2 3 – ( ξ – η ) 2 3 ] = 4 , ⇒ ( ξ + η ) 2 3 – ( ξ – η ) 2 3 = 4 4 3 , ⇒ ( ξ + η ) 2 3 – ( ξ – η ) 2 3 = 4 2 3 . \large \begin {align*} & \sqrt [ \large 3 \normalsize ] { 4 } \left [ { { { \left ( { \xi + \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } – { { \left ( { \xi – \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ] = { { x ^ 2 } + 2 + \frac { 1 }{ { { x ^ 2 } } } – \left ( { { x ^ 2 } – 2 + \frac { 1 } { { { x ^ 2 } } } } \right ) , \; \; } \\ & \Rightarrow { \sqrt [ \large 3 \normalsize ] { 4 } \left [ { { { \left ( { \xi + \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } – { { \left ( { \xi – \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ] = 4 , \; \; } \Rightarrow { \sqrt [ \large 3 \normalsize ] { 4 } \left [ { { { \left ( { \xi + \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } – { { \left ( { \xi – \eta } \right ) } ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ] = 4 , \; \; } \\ & \Rightarrow { { \left ( { \xi + \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } – { \left ( { \xi – \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } = \frac { 4 } { { \sqrt [ \large 3 \normalsize ] { 4 } } } , \; \; } \Rightarrow { { \left ( { \xi + \eta } \right ) ^ { \large \frac { 2 } { 3 } \normalsize } } – { \left ( { \xi – \eta } \right ) ^ { \large \frac { 2 }{ 3 } \normalsize } } = { 4 ^ { \large \frac { 2 } { 3 } \normalsize } } . } \end {align*} 3 4 [ ( ξ + η ) 3 2 – ( ξ – η ) 3 2 ] = x 2 + 2 + x 2 1 – ( x 2 –2 + x 2 1 ) , ⇒ 3 4 [ ( ξ + η ) 3 2 – ( ξ – η ) 3 2 ] = 4 , ⇒ 3 4 [ ( ξ + η ) 3 2 – ( ξ – η ) 3 2 ] = 4 , ⇒ ( ξ + η ) 3 2 – ( ξ – η ) 3 2 = 3 4 4 , ⇒ ( ξ + η ) 3 2 – ( ξ – η ) 3 2 = 4 3 2 .
در نتیجه، معادله گسترنده منحنی هذلولوی را به فرم ضمنی f ( ξ , η ) = 0 f\left( {\xi ,\eta } \right) = 0 f ( ξ , η ) = 0