گراف دو همبند (Biconnected Graph) — از صفر تا صد
در این مطلب، مفهوم گراف دو همبند و مولفه دو همبند مورد بررسی قرار میگیرد و روش تشخیص هر یک از آنها بیان میشود. همچنین، پیادهسازی روشهای بیان شده در زبانهای برنامهنویسی گوناگون شامل «سیپلاسپلاس» (++C)، «جاوا» (Java)، «پایتون ۳» (Python 3) انجام خواهد شد.
یک گراف بدون جهت، «دو همبند» (Biconnected Graph) نامیده میشود اگر بین هر دو «راس» (Node) آن، حداقل دو مسیر مجزا وجود داشته باشد. در یک گراف دو همبند، چرخه سادهای بین هر دو راس وجود دارد. بر اساس قرارداد، دو گره متصل شده به وسیله یک یال، یک گراف دو همبند میسازند؛ اما این مورد، خصوصیت بیان شده در خط پیشین را تایید نمیکند. برای یک گراف با بیش از دو راس، خصوصیت بالا باید وجود داشته باشد تا گراف دو همبند محسوب شود. مثالهایی از گراف دو همبند و غیر دو همبند در ادامه آمده است.

روش بررسی دو همبند بودن یک گراف
یک گراف دو همبند است اگر همبند باشد و هیچ «راس برشی» (ٰArticulation Point) نداشته باشد. بنابراین، برای تشخیص گراف دو همبند، نیاز به تشخیص دو چیز در یک گراف است:
- گراف همبند باشد.
- هیچ راس برشی در گراف وجود نداشته باشد.
کار را میتوان از هر راسی آغاز کرد و «پیمایش جستجوی اول عمق» (Depth-First Search Traversal | DFS) را انجام داد. در پیمایش DFS، بررسی میشود که آیا راس برشی وجود دارد یا خیر. اگر هیچ راس برشی پیدا نشد، گراف دو همبند است. در نهایت، باید بررسی شود که آیا همه راسها از پیمایش جستجوی اول عمق در دسترس هستند یا خیر. اگر همه راسها در دسترس نباشند بدین معنا است که گراف حتی متصل نیز نیست. در ادامه، پیادهسازی رویکرد بیان شده در زبانهای برنامهنویسی گوناگون ارائه شده است.
برنامه تشخیص گراف دو همبند در ++C
1// A C++ program to find if a given undirected graph is
2// biconnected
3#include<iostream>
4#include <list>
5#define NIL -1
6using namespace std;
7
8// A class that represents an undirected graph
9class Graph
10{
11 int V; // No. of vertices
12 list<int> *adj; // A dynamic array of adjacency lists
13 bool isBCUtil(int v, bool visited[], int disc[], int low[],
14 int parent[]);
15public:
16 Graph(int V); // Constructor
17 void addEdge(int v, int w); // to add an edge to graph
18 bool isBC(); // returns true if graph is Biconnected
19};
20
21Graph::Graph(int V)
22{
23 this->V = V;
24 adj = new list<int>[V];
25}
26
27void Graph::addEdge(int v, int w)
28{
29 adj[v].push_back(w);
30 adj[w].push_back(v); // Note: the graph is undirected
31}
32
33// A recursive function that returns true if there is an articulation
34// point in given graph, otherwise returns false.
35// This function is almost same as isAPUtil() here ( http://goo.gl/Me9Fw )
36// u --> The vertex to be visited next
37// visited[] --> keeps tract of visited vertices
38// disc[] --> Stores discovery times of visited vertices
39// parent[] --> Stores parent vertices in DFS tree
40bool Graph::isBCUtil(int u, bool visited[], int disc[],int low[],int parent[])
41{
42 // A static variable is used for simplicity, we can avoid use of static
43 // variable by passing a pointer.
44 static int time = 0;
45
46 // Count of children in DFS Tree
47 int children = 0;
48
49 // Mark the current node as visited
50 visited[u] = true;
51
52 // Initialize discovery time and low value
53 disc[u] = low[u] = ++time;
54
55 // Go through all vertices aadjacent to this
56 list<int>::iterator i;
57 for (i = adj[u].begin(); i != adj[u].end(); ++i)
58 {
59 int v = *i; // v is current adjacent of u
60
61 // If v is not visited yet, then make it a child of u
62 // in DFS tree and recur for it
63 if (!visited[v])
64 {
65 children++;
66 parent[v] = u;
67
68 // check if subgraph rooted with v has an articulation point
69 if (isBCUtil(v, visited, disc, low, parent))
70 return true;
71
72 // Check if the subtree rooted with v has a connection to
73 // one of the ancestors of u
74 low[u] = min(low[u], low[v]);
75
76 // u is an articulation point in following cases
77
78 // (1) u is root of DFS tree and has two or more chilren.
79 if (parent[u] == NIL && children > 1)
80 return true;
81
82 // (2) If u is not root and low value of one of its child is
83 // more than discovery value of u.
84 if (parent[u] != NIL && low[v] >= disc[u])
85 return true;
86 }
87
88 // Update low value of u for parent function calls.
89 else if (v != parent[u])
90 low[u] = min(low[u], disc[v]);
91 }
92 return false;
93}
94
95// The main function that returns true if graph is Biconnected,
96// otherwise false. It uses recursive function isBCUtil()
97bool Graph::isBC()
98{
99 // Mark all the vertices as not visited
100 bool *visited = new bool[V];
101 int *disc = new int[V];
102 int *low = new int[V];
103 int *parent = new int[V];
104
105 // Initialize parent and visited, and ap(articulation point)
106 // arrays
107 for (int i = 0; i < V; i++)
108 {
109 parent[i] = NIL;
110 visited[i] = false;
111 }
112
113 // Call the recursive helper function to find if there is an articulation
114 // point in given graph. We do DFS traversal starring from vertex 0
115 if (isBCUtil(0, visited, disc, low, parent) == true)
116 return false;
117
118 // Now check whether the given graph is connected or not. An undirected
119 // graph is connected if all vertices are reachable from any starting
120 // point (we have taken 0 as starting point)
121 for (int i = 0; i < V; i++)
122 if (visited[i] == false)
123 return false;
124
125 return true;
126}
127
128// Driver program to test above function
129int main()
130{
131 // Create graphs given in above diagrams
132 Graph g1(2);
133 g1.addEdge(0, 1);
134 g1.isBC()? cout << "Yes\n" : cout << "No\n";
135
136 Graph g2(5);
137 g2.addEdge(1, 0);
138 g2.addEdge(0, 2);
139 g2.addEdge(2, 1);
140 g2.addEdge(0, 3);
141 g2.addEdge(3, 4);
142 g2.addEdge(2, 4);
143 g2.isBC()? cout << "Yes\n" : cout << "No\n";
144
145 Graph g3(3);
146 g3.addEdge(0, 1);
147 g3.addEdge(1, 2);
148 g3.isBC()? cout << "Yes\n" : cout << "No\n";
149
150 Graph g4(5);
151 g4.addEdge(1, 0);
152 g4.addEdge(0, 2);
153 g4.addEdge(2, 1);
154 g4.addEdge(0, 3);
155 g4.addEdge(3, 4);
156 g4.isBC()? cout << "Yes\n" : cout << "No\n";
157
158 Graph g5(3);
159 g5.addEdge(0, 1);
160 g5.addEdge(1, 2);
161 g5.addEdge(2, 0);
162 g5.isBC()? cout << "Yes\n" : cout << "No\n";
163
164 return 0;
165}برنامه تشخیص گراف دو همبند در جاوا
1// A Java program to find if a given undirected graph is
2// biconnected
3import java.io.*;
4import java.util.*;
5import java.util.LinkedList;
6
7// This class represents a directed graph using adjacency
8// list representation
9class Graph
10{
11 private int V; // No. of vertices
12
13 // Array of lists for Adjacency List Representation
14 private LinkedList<Integer> adj[];
15
16 int time = 0;
17 static final int NIL = -1;
18
19 // Constructor
20 Graph(int v)
21 {
22 V = v;
23 adj = new LinkedList[v];
24 for (int i=0; i<v; ++i)
25 adj[i] = new LinkedList();
26 }
27
28 //Function to add an edge into the graph
29 void addEdge(int v, int w)
30 {
31 adj[v].add(w); //Note that the graph is undirected.
32 adj[w].add(v);
33 }
34
35 // A recursive function that returns true if there is an articulation
36 // point in given graph, otherwise returns false.
37 // This function is almost same as isAPUtil() @ http://goo.gl/Me9Fw
38 // u --> The vertex to be visited next
39 // visited[] --> keeps tract of visited vertices
40 // disc[] --> Stores discovery times of visited vertices
41 // parent[] --> Stores parent vertices in DFS tree
42 boolean isBCUtil(int u, boolean visited[], int disc[],int low[],
43 int parent[])
44 {
45
46 // Count of children in DFS Tree
47 int children = 0;
48
49 // Mark the current node as visited
50 visited[u] = true;
51
52 // Initialize discovery time and low value
53 disc[u] = low[u] = ++time;
54
55 // Go through all vertices aadjacent to this
56 Iterator<Integer> i = adj[u].iterator();
57 while (i.hasNext())
58 {
59 int v = i.next(); // v is current adjacent of u
60
61 // If v is not visited yet, then make it a child of u
62 // in DFS tree and recur for it
63 if (!visited[v])
64 {
65 children++;
66 parent[v] = u;
67
68 // check if subgraph rooted with v has an articulation point
69 if (isBCUtil(v, visited, disc, low, parent))
70 return true;
71
72 // Check if the subtree rooted with v has a connection to
73 // one of the ancestors of u
74 low[u] = Math.min(low[u], low[v]);
75
76 // u is an articulation point in following cases
77
78 // (1) u is root of DFS tree and has two or more chilren.
79 if (parent[u] == NIL && children > 1)
80 return true;
81
82 // (2) If u is not root and low value of one of its
83 // child is more than discovery value of u.
84 if (parent[u] != NIL && low[v] >= disc[u])
85 return true;
86 }
87
88 // Update low value of u for parent function calls.
89 else if (v != parent[u])
90 low[u] = Math.min(low[u], disc[v]);
91 }
92 return false;
93 }
94
95 // The main function that returns true if graph is Biconnected,
96 // otherwise false. It uses recursive function isBCUtil()
97 boolean isBC()
98 {
99 // Mark all the vertices as not visited
100 boolean visited[] = new boolean[V];
101 int disc[] = new int[V];
102 int low[] = new int[V];
103 int parent[] = new int[V];
104
105 // Initialize parent and visited, and ap(articulation point)
106 // arrays
107 for (int i = 0; i < V; i++)
108 {
109 parent[i] = NIL;
110 visited[i] = false;
111 }
112
113 // Call the recursive helper function to find if there is an
114 // articulation/ point in given graph. We do DFS traversal
115 // starring from vertex 0
116 if (isBCUtil(0, visited, disc, low, parent) == true)
117 return false;
118
119 // Now check whether the given graph is connected or not.
120 // An undirected graph is connected if all vertices are
121 // reachable from any starting point (we have taken 0 as
122 // starting point)
123 for (int i = 0; i < V; i++)
124 if (visited[i] == false)
125 return false;
126
127 return true;
128 }
129
130 // Driver method
131 public static void main(String args[])
132 {
133 // Create graphs given in above diagrams
134 Graph g1 =new Graph(2);
135 g1.addEdge(0, 1);
136 if (g1.isBC())
137 System.out.println("Yes");
138 else
139 System.out.println("No");
140
141 Graph g2 =new Graph(5);
142 g2.addEdge(1, 0);
143 g2.addEdge(0, 2);
144 g2.addEdge(2, 1);
145 g2.addEdge(0, 3);
146 g2.addEdge(3, 4);
147 g2.addEdge(2, 4);
148 if (g2.isBC())
149 System.out.println("Yes");
150 else
151 System.out.println("No");
152
153 Graph g3 = new Graph(3);
154 g3.addEdge(0, 1);
155 g3.addEdge(1, 2);
156 if (g3.isBC())
157 System.out.println("Yes");
158 else
159 System.out.println("No");
160
161 Graph g4 = new Graph(5);
162 g4.addEdge(1, 0);
163 g4.addEdge(0, 2);
164 g4.addEdge(2, 1);
165 g4.addEdge(0, 3);
166 g4.addEdge(3, 4);
167 if (g4.isBC())
168 System.out.println("Yes");
169 else
170 System.out.println("No");
171
172 Graph g5= new Graph(3);
173 g5.addEdge(0, 1);
174 g5.addEdge(1, 2);
175 g5.addEdge(2, 0);
176 if (g5.isBC())
177 System.out.println("Yes");
178 else
179 System.out.println("No");
180 }
181}
182// This code is contributed by Aakash Hasija برنامه تشخیص گراف دو همبند در پایتون
1# Python program to find if a given undirected graph is
2# biconnected
3
4from collections import defaultdict
5
6#This class represents an undirected graph using adjacency list representation
7class Graph:
8
9 def __init__(self,vertices):
10 self.V= vertices #No. of vertices
11 self.graph = defaultdict(list) # default dictionary to store graph
12 self.Time = 0
13
14 # function to add an edge to graph
15 def addEdge(self,u,v):
16 self.graph[u].append(v)
17 self.graph[v].append(u)
18
19 '''A recursive function that returns true if there is an articulation
20 point in given graph, otherwise returns false.
21 This function is almost same as isAPUtil()
22 u --> The vertex to be visited next
23 visited[] --> keeps tract of visited vertices
24 disc[] --> Stores discovery times of visited vertices
25 parent[] --> Stores parent vertices in DFS tree'''
26 def isBCUtil(self,u, visited, parent, low, disc):
27
28 #Count of children in current node
29 children =0
30
31 # Mark the current node as visited and print it
32 visited[u]= True
33
34 # Initialize discovery time and low value
35 disc[u] = self.Time
36 low[u] = self.Time
37 self.Time += 1
38
39 #Recur for all the vertices adjacent to this vertex
40 for v in self.graph[u]:
41 # If v is not visited yet, then make it a child of u
42 # in DFS tree and recur for it
43 if visited[v] == False :
44 parent[v] = u
45 children += 1
46 if self.isBCUtil(v, visited, parent, low, disc):
47 return True
48
49 # Check if the subtree rooted with v has a connection to
50 # one of the ancestors of u
51 low[u] = min(low[u], low[v])
52
53 # u is an articulation point in following cases
54 # (1) u is root of DFS tree and has two or more chilren.
55 if parent[u] == -1 and children > 1:
56 return True
57
58 #(2) If u is not root and low value of one of its child is more
59 # than discovery value of u.
60 if parent[u] != -1 and low[v] >= disc[u]:
61 return True
62
63 elif v != parent[u]: # Update low value of u for parent function calls.
64 low[u] = min(low[u], disc[v])
65
66 return False
67
68
69 # The main function that returns true if graph is Biconnected,
70 # otherwise false. It uses recursive function isBCUtil()
71 def isBC(self):
72
73 # Mark all the vertices as not visited and Initialize parent and visited,
74 # and ap(articulation point) arrays
75 visited = [False] * (self.V)
76 disc = [float("Inf")] * (self.V)
77 low = [float("Inf")] * (self.V)
78 parent = [-1] * (self.V)
79
80
81 # Call the recursive helper function to find if there is an
82 # articulation points in given graph. We do DFS traversal starting
83 # from vertex 0
84 if self.isBCUtil(0, visited, parent, low, disc):
85 return False
86
87 '''Now check whether the given graph is connected or not.
88 An undirected graph is connected if all vertices are
89 reachable from any starting point (we have taken 0 as
90 starting point)'''
91 if any(i == False for i in visited):
92 return False
93
94 return True
95
96# Create a graph given in the above diagram
97g1 = Graph(2)
98g1.addEdge(0, 1)
99print "Yes" if g1.isBC() else "No"
100
101g2 = Graph(5)
102g2.addEdge(1, 0)
103g2.addEdge(0, 2)
104g2.addEdge(2, 1)
105g2.addEdge(0, 3)
106g2.addEdge(3, 4)
107g2.addEdge(2, 4)
108print "Yes" if g2.isBC() else "No"
109
110g3 = Graph(3)
111g3.addEdge(0, 1)
112g3.addEdge(1, 2)
113print "Yes" if g3.isBC() else "No"
114
115
116g4 = Graph (5)
117g4.addEdge(1, 0)
118g4.addEdge(0, 2)
119g4.addEdge(2, 1)
120g4.addEdge(0, 3)
121g4.addEdge(3, 4)
122print "Yes" if g4.isBC() else "No"
123
124g5 = Graph(3)
125g5.addEdge(0, 1)
126g5.addEdge(1, 2)
127g5.addEdge(2, 0)
128print "Yes" if g5.isBC() else "No"
129
130#This code is contributed by Neelam Yadavخروجی قطعه کدهای بالا، به صورت زیر است.
Yes Yes No No Yes
تابع بالا، یک DFS ساده با آرایههای اضافی است. بنابراین، پیچیدگی زمانی آن مشابه با DFS و برای ارائه لیست همجواری گراف، برابر با O(V+E) است.
برنامه تشخیص مولفه دو همبند (Biconnected Components)
یک «مولفه دو همبند» (Biconnected Components) یک زیر گراف حداکثر دو همبند است. در این مطلب، روش نوشتن برنامه تشخیص مولفه دو همبند در گراف با استفاده از الگوریتم ارائه شده توسط «جان هاپکرافت» (John Hopcroft) و «رابرت تارجان» (Robert Tarjan) آموزش داده شده است.
همچنین، پیادهسازی روش ارائه شده، در زبانهای «سیپلاسپلاس» (++C)، «جاوا» (Java) و «پایتون ۳» (Python 3) انجام شده است.
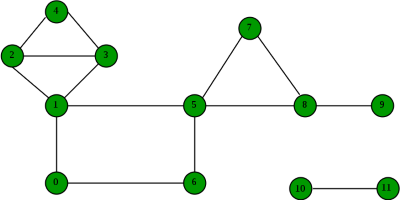
در گراف بالا، مولفههای دو همبند به شرح زیر هستند:
4–2 3–4 3–1 2–3 1–2
8–9
8–5 7–8 5–7
6–0 5–6 1–5 0–1
10–11
الگوریتم ارائه شده برای تشخیص مولفه دو همبند، بر پایه Disc و Low Valueهای موجود در قطعه کدهای مربوط به گراف دو همبند است. هدف، ذخیرهسازی یالهای ملاقات شده در پشته در حالی است که جستجوی اول عمق (Depth First Search) روی گراف انجام و به دنبال «راسهای برشی» (Articulation Point) گشته میشود.
به محض اینکه راس برشی پیدا شود، همه راسهای ملاقات شده در طول DFS از نود u به بعد یک مولفه دو همبند را تشکیل میدهند. هنگامی که DFS برای یک مولفه همبند انجام شد، همه راسهای ارائه شده در پشته یک مولفه دو همبند را تشکیل میدهند. اگر هیچ راس برشی در گراف وجود نداشته باشد، گراف دو همبند است و بنابراین، یک مولفه دو همبند وجود دارد که خود گراف است.
برنامه تشخیص مولفه دو همبند در ++C
1// A C++ program to find biconnected components in a given undirected graph
2#include <iostream>
3#include <list>
4#include <stack>
5#define NIL -1
6using namespace std;
7int count = 0;
8class Edge {
9public:
10 int u;
11 int v;
12 Edge(int u, int v);
13};
14Edge::Edge(int u, int v)
15{
16 this->u = u;
17 this->v = v;
18}
19
20// A class that represents an directed graph
21class Graph {
22 int V; // No. of vertices
23 int E; // No. of edges
24 list<int>* adj; // A dynamic array of adjacency lists
25
26 // A Recursive DFS based function used by BCC()
27 void BCCUtil(int u, int disc[], int low[],
28 list<Edge>* st, int parent[]);
29
30public:
31 Graph(int V); // Constructor
32 void addEdge(int v, int w); // function to add an edge to graph
33 void BCC(); // prints strongly connected components
34};
35
36Graph::Graph(int V)
37{
38 this->V = V;
39 this->E = 0;
40 adj = new list<int>[V];
41}
42
43void Graph::addEdge(int v, int w)
44{
45 adj[v].push_back(w);
46 E++;
47}
48
49// A recursive function that finds and prints strongly connected
50// components using DFS traversal
51// u --> The vertex to be visited next
52// disc[] --> Stores discovery times of visited vertices
53// low[] -- >> earliest visited vertex (the vertex with minimum
54// discovery time) that can be reached from subtree
55// rooted with current vertex
56// *st -- >> To store visited edges
57void Graph::BCCUtil(int u, int disc[], int low[], list<Edge>* st,
58 int parent[])
59{
60 // A static variable is used for simplicity, we can avoid use
61 // of static variable by passing a pointer.
62 static int time = 0;
63
64 // Initialize discovery time and low value
65 disc[u] = low[u] = ++time;
66 int children = 0;
67
68 // Go through all vertices adjacent to this
69 list<int>::iterator i;
70 for (i = adj[u].begin(); i != adj[u].end(); ++i) {
71 int v = *i; // v is current adjacent of 'u'
72
73 // If v is not visited yet, then recur for it
74 if (disc[v] == -1) {
75 children++;
76 parent[v] = u;
77 // store the edge in stack
78 st->push_back(Edge(u, v));
79 BCCUtil(v, disc, low, st, parent);
80
81 // Check if the subtree rooted with 'v' has a
82 // connection to one of the ancestors of 'u'
83 // Case 1 -- per Strongly Connected Components Article
84 low[u] = min(low[u], low[v]);
85
86 // If u is an articulation point,
87 // pop all edges from stack till u -- v
88 if ((disc[u] == 1 && children > 1) || (disc[u] > 1 && low[v] >= disc[u])) {
89 while (st->back().u != u || st->back().v != v) {
90 cout << st->back().u << "--" << st->back().v << " ";
91 st->pop_back();
92 }
93 cout << st->back().u << "--" << st->back().v;
94 st->pop_back();
95 cout << endl;
96 count++;
97 }
98 }
99
100 // Update low value of 'u' only of 'v' is still in stack
101 // (i.e. it's a back edge, not cross edge).
102 // Case 2 -- per Strongly Connected Components Article
103 else if (v != parent[u]) {
104 low[u] = min(low[u], disc[v]);
105 if (disc[v] < disc[u]) {
106 st->push_back(Edge(u, v));
107 }
108 }
109 }
110}
111
112// The function to do DFS traversal. It uses BCCUtil()
113void Graph::BCC()
114{
115 int* disc = new int[V];
116 int* low = new int[V];
117 int* parent = new int[V];
118 list<Edge>* st = new list<Edge>[E];
119
120 // Initialize disc and low, and parent arrays
121 for (int i = 0; i < V; i++) {
122 disc[i] = NIL;
123 low[i] = NIL;
124 parent[i] = NIL;
125 }
126
127 for (int i = 0; i < V; i++) {
128 if (disc[i] == NIL)
129 BCCUtil(i, disc, low, st, parent);
130
131 int j = 0;
132 // If stack is not empty, pop all edges from stack
133 while (st->size() > 0) {
134 j = 1;
135 cout << st->back().u << "--" << st->back().v << " ";
136 st->pop_back();
137 }
138 if (j == 1) {
139 cout << endl;
140 count++;
141 }
142 }
143}
144
145// Driver program to test above function
146int main()
147{
148 Graph g(12);
149 g.addEdge(0, 1);
150 g.addEdge(1, 0);
151 g.addEdge(1, 2);
152 g.addEdge(2, 1);
153 g.addEdge(1, 3);
154 g.addEdge(3, 1);
155 g.addEdge(2, 3);
156 g.addEdge(3, 2);
157 g.addEdge(2, 4);
158 g.addEdge(4, 2);
159 g.addEdge(3, 4);
160 g.addEdge(4, 3);
161 g.addEdge(1, 5);
162 g.addEdge(5, 1);
163 g.addEdge(0, 6);
164 g.addEdge(6, 0);
165 g.addEdge(5, 6);
166 g.addEdge(6, 5);
167 g.addEdge(5, 7);
168 g.addEdge(7, 5);
169 g.addEdge(5, 8);
170 g.addEdge(8, 5);
171 g.addEdge(7, 8);
172 g.addEdge(8, 7);
173 g.addEdge(8, 9);
174 g.addEdge(9, 8);
175 g.addEdge(10, 11);
176 g.addEdge(11, 10);
177 g.BCC();
178 cout << "Above are " << count << " biconnected components in graph";
179 return 0;
180}برنامه تشخیص مولفه دو همبند در جاوا
1// A Java program to find biconnected components in a given
2// undirected graph
3import java.io.*;
4import java.util.*;
5
6// This class represents a directed graph using adjacency
7// list representation
8class Graph {
9 private int V, E; // No. of vertices & Edges respectively
10 private LinkedList<Integer> adj[]; // Adjacency List
11
12 // Count is number of biconnected components. time is
13 // used to find discovery times
14 static int count = 0, time = 0;
15
16 class Edge {
17 int u;
18 int v;
19 Edge(int u, int v)
20 {
21 this.u = u;
22 this.v = v;
23 }
24 };
25
26 // Constructor
27 Graph(int v)
28 {
29 V = v;
30 E = 0;
31 adj = new LinkedList[v];
32 for (int i = 0; i < v; ++i)
33 adj[i] = new LinkedList();
34 }
35
36 // Function to add an edge into the graph
37 void addEdge(int v, int w)
38 {
39 adj[v].add(w);
40 E++;
41 }
42
43 // A recursive function that finds and prints strongly connected
44 // components using DFS traversal
45 // u --> The vertex to be visited next
46 // disc[] --> Stores discovery times of visited vertices
47 // low[] -- >> earliest visited vertex (the vertex with minimum
48 // discovery time) that can be reached from subtree
49 // rooted with current vertex
50 // *st -- >> To store visited edges
51 void BCCUtil(int u, int disc[], int low[], LinkedList<Edge> st,
52 int parent[])
53 {
54
55 // Initialize discovery time and low value
56 disc[u] = low[u] = ++time;
57 int children = 0;
58
59 // Go through all vertices adjacent to this
60 Iterator<Integer> it = adj[u].iterator();
61 while (it.hasNext()) {
62 int v = it.next(); // v is current adjacent of 'u'
63
64 // If v is not visited yet, then recur for it
65 if (disc[v] == -1) {
66 children++;
67 parent[v] = u;
68
69 // store the edge in stack
70 st.add(new Edge(u, v));
71 BCCUtil(v, disc, low, st, parent);
72
73 // Check if the subtree rooted with 'v' has a
74 // connection to one of the ancestors of 'u'
75 // Case 1 -- per Strongly Connected Components Article
76 if (low[u] > low[v])
77 low[u] = low[v];
78
79 // If u is an articulation point,
80 // pop all edges from stack till u -- v
81 if ((disc[u] == 1 && children > 1) || (disc[u] > 1 && low[v] >= disc[u])) {
82 while (st.getLast().u != u || st.getLast().v != v) {
83 System.out.print(st.getLast().u + "--" + st.getLast().v + " ");
84 st.removeLast();
85 }
86 System.out.println(st.getLast().u + "--" + st.getLast().v + " ");
87 st.removeLast();
88
89 count++;
90 }
91 }
92
93 // Update low value of 'u' only if 'v' is still in stack
94 // (i.e. it's a back edge, not cross edge).
95 // Case 2 -- per Strongly Connected Components Article
96 else if (v != parent[u] && disc[v] < disc[u] ) {
97 if (low[u] > disc[v])
98 low[u] = disc[v];
99
100 st.add(new Edge(u, v));
101 }
102 }
103 }
104
105 // The function to do DFS traversal. It uses BCCUtil()
106 void BCC()
107 {
108 int disc[] = new int[V];
109 int low[] = new int[V];
110 int parent[] = new int[V];
111 LinkedList<Edge> st = new LinkedList<Edge>();
112
113 // Initialize disc and low, and parent arrays
114 for (int i = 0; i < V; i++) {
115 disc[i] = -1;
116 low[i] = -1;
117 parent[i] = -1;
118 }
119
120 for (int i = 0; i < V; i++) {
121 if (disc[i] == -1)
122 BCCUtil(i, disc, low, st, parent);
123
124 int j = 0;
125
126 // If stack is not empty, pop all edges from stack
127 while (st.size() > 0) {
128 j = 1;
129 System.out.print(st.getLast().u + "--" + st.getLast().v + " ");
130 st.removeLast();
131 }
132 if (j == 1) {
133 System.out.println();
134 count++;
135 }
136 }
137 }
138
139 public static void main(String args[])
140 {
141 Graph g = new Graph(12);
142 g.addEdge(0, 1);
143 g.addEdge(1, 0);
144 g.addEdge(1, 2);
145 g.addEdge(2, 1);
146 g.addEdge(1, 3);
147 g.addEdge(3, 1);
148 g.addEdge(2, 3);
149 g.addEdge(3, 2);
150 g.addEdge(2, 4);
151 g.addEdge(4, 2);
152 g.addEdge(3, 4);
153 g.addEdge(4, 3);
154 g.addEdge(1, 5);
155 g.addEdge(5, 1);
156 g.addEdge(0, 6);
157 g.addEdge(6, 0);
158 g.addEdge(5, 6);
159 g.addEdge(6, 5);
160 g.addEdge(5, 7);
161 g.addEdge(7, 5);
162 g.addEdge(5, 8);
163 g.addEdge(8, 5);
164 g.addEdge(7, 8);
165 g.addEdge(8, 7);
166 g.addEdge(8, 9);
167 g.addEdge(9, 8);
168 g.addEdge(10, 11);
169 g.addEdge(11, 10);
170
171 g.BCC();
172
173 System.out.println("Above are " + g.count + " biconnected components in graph");
174 }
175}
176// This code is contributed by Aakash Hasijaبرنامه تشخیص مولفه دو همبند در پایتون
1# Python program to find biconnected components in a given
2# undirected graph
3# Complexity : O(V + E)
4
5
6from collections import defaultdict
7
8# This class represents an directed graph
9# using adjacency list representation
10class Graph:
11
12 def __init__(self, vertices):
13 # No. of vertices
14 self.V = vertices
15
16 # default dictionary to store graph
17 self.graph = defaultdict(list)
18
19 # time is used to find discovery times
20 self.Time = 0
21
22 # Count is number of biconnected components
23 self.count = 0
24
25 # function to add an edge to graph
26 def addEdge(self, u, v):
27 self.graph[u].append(v)
28 self.graph[v].append(u)
29
30 '''A recursive function that finds and prints strongly connected
31 components using DFS traversal
32 u --> The vertex to be visited next
33 disc[] --> Stores discovery times of visited vertices
34 low[] -- >> earliest visited vertex (the vertex with minimum
35 discovery time) that can be reached from subtree
36 rooted with current vertex
37 st -- >> To store visited edges'''
38 def BCCUtil(self, u, parent, low, disc, st):
39
40 # Count of children in current node
41 children = 0
42
43 # Initialize discovery time and low value
44 disc[u] = self.Time
45 low[u] = self.Time
46 self.Time += 1
47
48
49 # Recur for all the vertices adjacent to this vertex
50 for v in self.graph[u]:
51 # If v is not visited yet, then make it a child of u
52 # in DFS tree and recur for it
53 if disc[v] == -1 :
54 parent[v] = u
55 children += 1
56 st.append((u, v)) # store the edge in stack
57 self.BCCUtil(v, parent, low, disc, st)
58
59 # Check if the subtree rooted with v has a connection to
60 # one of the ancestors of u
61 # Case 1 -- per Strongly Connected Components Article
62 low[u] = min(low[u], low[v])
63
64 # If u is an articulation point, pop
65 # all edges from stack till (u, v)
66 if parent[u] == -1 and children > 1 or parent[u] != -1 and low[v] >= disc[u]:
67 self.count += 1 # increment count
68 w = -1
69 while w != (u, v):
70 w = st.pop()
71 print w,
72 print""
73
74 elif v != parent[u] and low[u] > disc[v]:
75 '''Update low value of 'u' only of 'v' is still in stack
76 (i.e. it's a back edge, not cross edge).
77 Case 2
78 -- per Strongly Connected Components Article'''
79
80 low[u] = min(low [u], disc[v])
81
82 st.append((u, v))
83
84
85 # The function to do DFS traversal.
86 # It uses recursive BCCUtil()
87 def BCC(self):
88
89 # Initialize disc and low, and parent arrays
90 disc = [-1] * (self.V)
91 low = [-1] * (self.V)
92 parent = [-1] * (self.V)
93 st = []
94
95 # Call the recursive helper function to
96 # find articulation points
97 # in DFS tree rooted with vertex 'i'
98 for i in range(self.V):
99 if disc[i] == -1:
100 self.BCCUtil(i, parent, low, disc, st)
101
102 # If stack is not empty, pop all edges from stack
103 if st:
104 self.count = self.count + 1
105
106 while st:
107 w = st.pop()
108 print w,
109 print ""
110
111# Create a graph given in the above diagram
112
113g = Graph(12)
114g.addEdge(0, 1)
115g.addEdge(1, 2)
116g.addEdge(1, 3)
117g.addEdge(2, 3)
118g.addEdge(2, 4)
119g.addEdge(3, 4)
120g.addEdge(1, 5)
121g.addEdge(0, 6)
122g.addEdge(5, 6)
123g.addEdge(5, 7)
124g.addEdge(5, 8)
125g.addEdge(7, 8)
126g.addEdge(8, 9)
127g.addEdge(10, 11)
128
129g.BCC();
130print ("Above are % d biconnected components in graph" %(g.count));
131
132# This code is contributed by Neelam Yadavخروجی قطعه کدهای بالا به صورت زیر است.
4--2 3--4 3--1 2--3 1--2 8--9 8--5 7--8 5--7 6--0 5--6 1--5 0--1 10--11 Above are 5 biconnected components in graph
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش ساختمان دادهها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- برنامه تشخیص وجود دور در گراف جهتدار — راهنمای کاربردی
- برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی
- یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
- الگوریتم بازی مار و پله همراه با کد — به زبان ساده
- حل مساله n وزیر با الگوریتم پسگرد (Backtracking) — به زبان ساده
^^













سلام
خواهشا یکم توی ترجمه بیشتر دقت کنید، مخصوصا سر معادل سازی اصطلاح ها و شرط های لازم و کافی، که احتمال بد فهمی کم شود.
متشکر!:)