کمان دایره چیست؟ – محاسبه طول و اندازه + حل مثال
کمان دایره شامل دو نقطه روی دایره و تمام نقاط بین آن دو نقطه است. به عبارت دیگر، کمان، قسمتی از محیط دایره محسوب میشود. در این آموزش از مجله فرادرس، ویژگیها، اجزا، روش رسم و محاسبه کمان دایره را معرفی میکنیم. به علاوه، ضمن حل چندین مثال متنوع، به برخی از سوالات پرتکرار در رابطه با کمان دایره پاسخ میدهیم.


دایره و اجزای آن
دایره، شکل مسطحی است که از یک منحنی بسته تشکیل میشود. تمام نقاط دایره، در فاصله مشخصی از یک نقطه ثابت قرار دارند. به این نقطه ثابت، مرکز دایره میگویند.
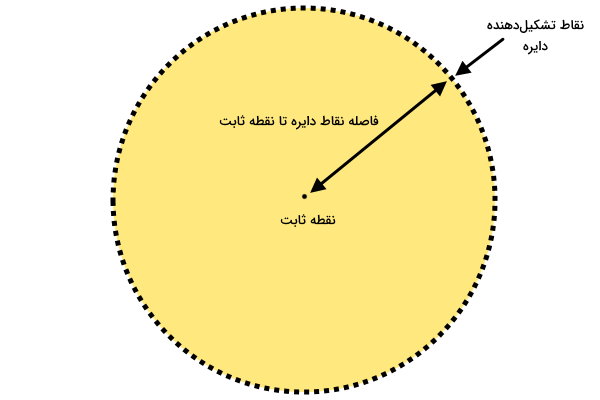
فاصله مرکز دایره تا محیط آن، با عنوان شعاع شناخته میشود. از دیگر اجزای دایره میتوان به وتر، قطر، کمان، قطاع، قطعه و مماس اشاره کرد.
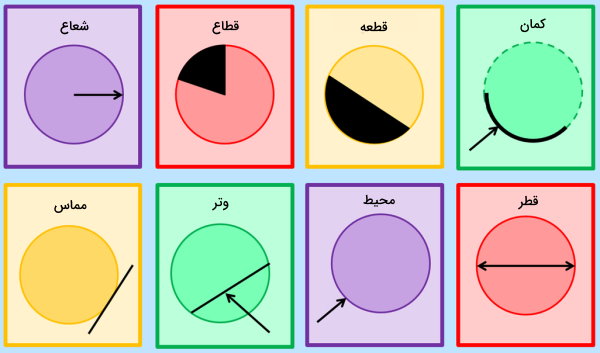
کمان دایره چیست؟
قوس یا «کمان» (Arc)، منحنی محدود به دو نقطه است. کمان دایره، به عنوان بخشی از دایره یا به طور دقیقتر، بخشی از محیط دایره تعریف میشود.
برای درک مفهوم کمان، با استفاده از مداد، یک دایره مانند دایره زیر رسم کنید. سپس، دو نقطه مانند نقاط الف و ب را بر روی محیط دایره در نظر بگیرید.
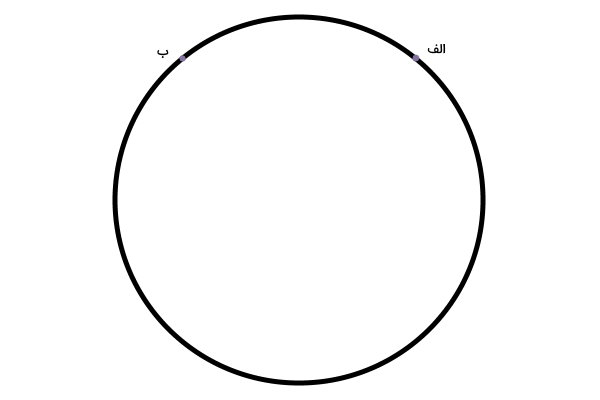
نقاط الف و ب، محیط دایره را به دو منحنی کوچک و بزرگ تقسیم میکنند. این منحنیها با عنوان کمان یا قوس دایره شناخته میشوند. در تصویر زیر، دو کمان محدود به نقاط الف و ب را با رنگهای متفاوت نمایش دادهایم. 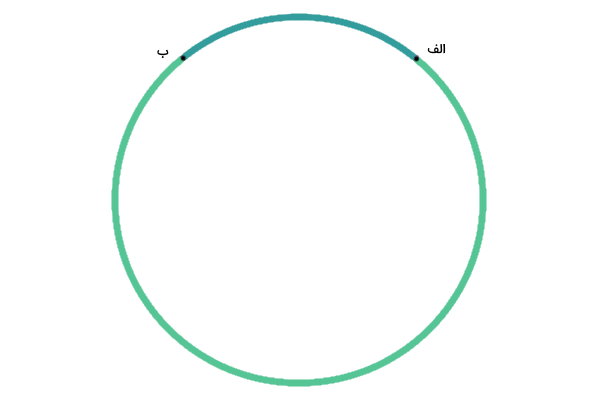
علامت کمان دایره چیست؟
در هندسه، قوس دایره، با علامت ⌒ در بالای حروف نقاط انتهایی آن نمایش داده میشود. به عنوان مثال، اگر بخواهیم کمان محدود به دو نقطه A و B بر روی محیط دایره را نمایش دهیم، از عبارت استفاده میکنیم. این عبارت را به صورت «کمان AB» میخوانیم.
ویژگی های کمان دایره چه هستند؟
ویژگیهای کمان، ارتباط نزدیکی با مفهوم زاویه مرکزی و محاطی دایره دارند. در بخشهای بعدی، به تعریف این زوایا خواهیم پرداخت. از مهمترین خواص کمان دایره میتوان به موارد زیر اشاره کرد:
- در یک دایره، زوایای مرکزی مقابل به کمانهایی با طول برابر، اندازه برابر دارند.
- زوایای محاطی مقابل یک کمان با هم برابر هستند.
- اندازه زاویه مرکزی مقابل یک کمان، دو برابر اندازه زاویه محاطی مقابل همان کمان است.
- در یک دایره، اگر دو کمان برابر باشند، وترهای نظیر آنها نیز با هم برابرند.
کمان دایره، بخشی از محیط آن است. محیط و مساحت، از مهمترین اندازههای دایره به شمار میروند. در صورت تمایل به یادگیری در مورد مساحت دایره، مطالعه مطلب «مساحت دایره به زبان ساده + فیلم آموزشی و حل تمرین» از مجله فرادرس را به شما پیشنهاد میکنیم.
کمان دایره چگونه رسم می شود ؟
پرگار، بهترین ابزار برای رسم دایره است. بنابراین، این ابزار معمولا به منظور رسم کمانهای دایره مورد استفاده قرار میگیرد.
به منظور رسم یک کمان، دهانه پرگار را به اندازه دلخواه (شعاع مورد نظر) باز میکنیم و سوزن آن را بر روی یک نقطه دلخواه (مرکز مورد نظر) قرار میدهیم.
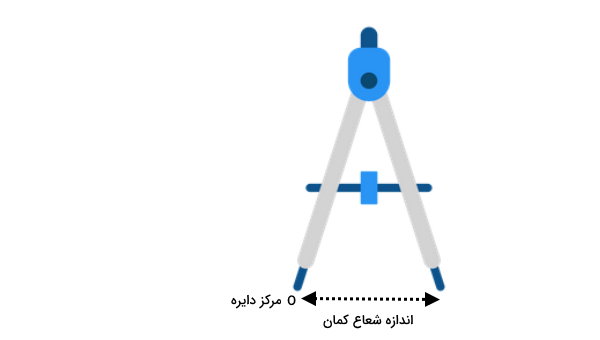
در مرحله بعد، پرگار را به اندازه دلخواه (طول کمان) میچرخانیم. به این ترتیب، کمان دایره رسم میشود.
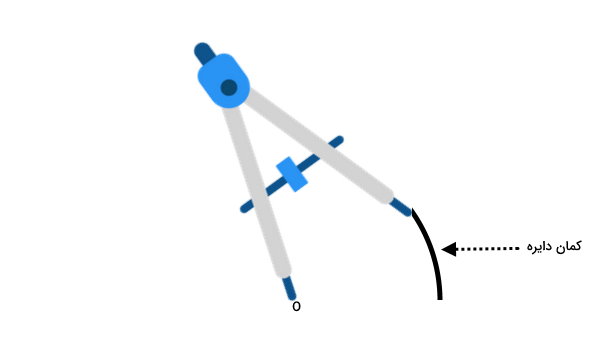
اندازه های کمان دایره چه هستند؟
کمان دایره، با دو اندازه طول کمان و زاویه مرکزی مشخص میشود. در ادامه، به تعریف این اندازهها میپردازیم. در بخش بعد نیز، روشهای تعیین طول و زاویه را مورد بررسی قرار میدهیم.
طول کمان دایره چیست ؟
کمان، بخشی از محیط دایره است. بر اساس این تعریف، طول کمان دایره، نسبتی از محیط دایره کامل خواهد بود. کمان دایره با واحدهای طول نظیر میلیمتر، سانتیمتر، متر و غیره بیان میشود. در ریاضیات، طول کمان را با حرف l در ابتدای عبارت جبری آن نمایش میدهند. به عنوان مثال، اگر طول برابر 7 سانتیمتر باشد، نمایش آن به صورت خواهد بود.
زاویه کمان دایره چیست ؟
زاویه مقابل کمان در مرکز دایره، با عنوان زاویه کمان یا زاویه مرکزی دایره شناخته میشود. اگر شعاعهای دایره را از دو انتهای کمان رسم کنیم، شکلی مشابه شکل زیر به وجود میآید.
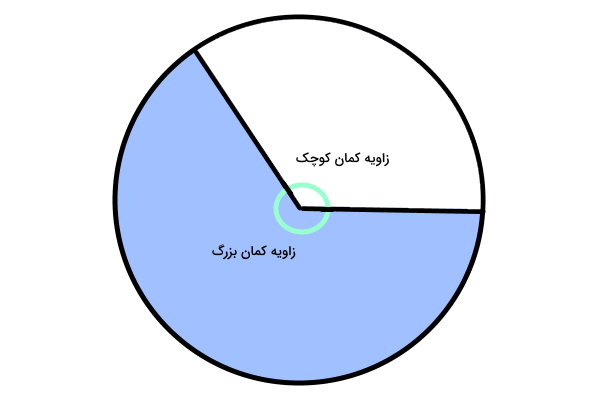
زاویه کمان را معمولا با حرف m در ابتدای عبارت جبری آن نمایش میدهند. به عنوان مثال، اگر زاویه برابر 40 درجه باشد، نمایش آن به صورت خواهد بود. توجه داشته باشید که دو کمان با زاویههای مرکزی برابر میتوانند دارای طولهای متفاوت باشند.
به عنوان مثال، در تصویر زیر، و برابر هستند. با این وجود، بزرگتر از است.

زاویه محاطی دایره چیست و چه رابطهای با زاویه مرکزی دارد؟
زاویه محاطی، زاویهای است که راس آن بر روی محیط دایره قرار دارد و ضلعهای آن، دایره را قطع کردهاند. تصویر زیر، نمونهای از یک زاویه محاطی را نمایش میدهد.
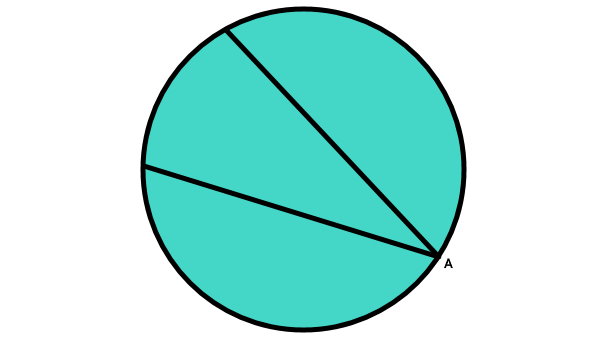
با استفاده از قانون جمع زوایای داخلی مثلث و زوایای مکمل میتوان ثابت کرد که اگر یکی از ضلعهای زاویه محاطی از مرکز دایره عبور کند (یکی از ضلعهای زاویه محاطی، قطر دایره باشد)، اندازه زاویه مرکزی مقابل کمان، دو برابر اندازه زاویه محاطی خواهد بود.
بر اساس خواص کمان دایره، تمام زوایای محاطی مقابل یک کمان، هماندازهاند. بنابراین، تمام زوایای مرکزی مقابل یک کمان، دو برابر زوایای محاطی مقابل آن کمان هستند.
زاویه ظلی چیست و چه رابطهای با زاویه مرکزی دارد؟
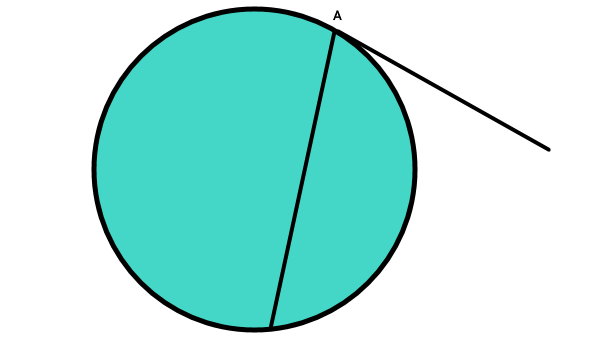
به زاویهای که راس آن بر روی دایره قرار گیرد، یکی از ضلعهای آن بر دایره مماس بوده و ضلع دیگر آن وتری از دایره باشد، زاویه ظلی میگویند. زاویه ظلی، نصف کمان روبهروی آن است.
زاویه و طول کمان دایره چگونه اندازه گیری می شود ؟
اندازهگیری زاویه کمان توسط روشهای دستی یا محاسباتی انجام میشود. برای اندازهگیری طول کمان نیز میتوان از فرمولهای مخصوص استفاده کرد.
تعیین دستی زاویه کمان
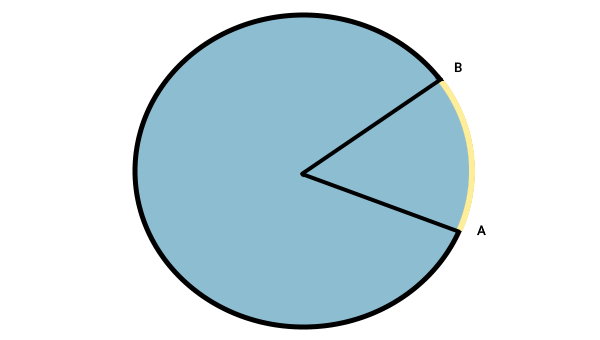
نقاله، وسیله مخصوص اندازهگیری زاویه شکلهای هندسی است. این وسیله، به منظور تعیین دسی زاویه کمان دایره نیز مورد استفاده قرار میگیرد. کمان BA در دایره زیر را در نظر بگیرید.

برای اندازهگیری زاویه مقابل این کمان، ابتدا شعاعهای دو انتهای آن را رسم میکنیم.
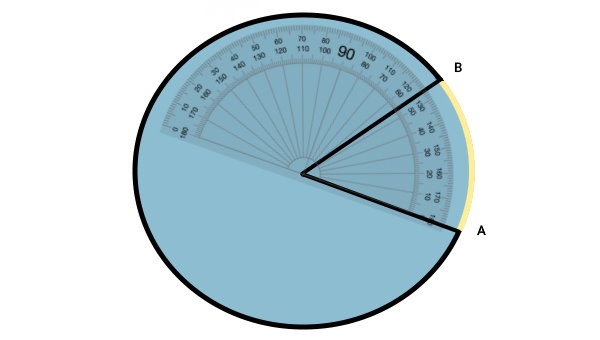
سپس، مرکز نقاله را بر روی مرکز دایره قرار میدهیم. اگر راستای خط زاویه صفر درجه را بر روی یکی از شعاعها منطبق کنیم، شعاع دیگر از روی عدد زاویه کمان عبور خواهد کرد. به عنوان مثال، در تصویر زیر، زاویه کمان برابر 55 درجه است.
محاسبه طول کمان
برای درک نحوه محاسبه طول کمان، ابتدا باید با فرمول محیط دایره آشنا شوید. این فرمول به صورت زیر نوشته میشود:
شعاع × عدد پی × 2 = محیط دایره کامل
زاویه یک دایره کامل برابر 360 درجه است. به عبارت دیگر، در صورتی که زاویه مقابل یک کمان، برابر 360 درجه باشد، طول آن با محیط دایره کامل برابر خواهد بود. اگر زاویه مقابل کمان، کمتر از 360 درجه باشد، طول آن از ضرب محیط دایره در نسبت زاویه کمان به 360 درجه بدست میآید.
بر اساس توضیحات بالا، فرمول طول کمان دایره برابر است با:
(360 ÷ زاویه کمان) × محیط دایره کامل = طول کمان
یا
(360 ÷ زاویه کمان) × شعاع × عدد پی × 2 = طول کمان
عبارت جبری طول کمان دایره به صورت زیر نوشته میشود:
- l: طول کمان
- r: شعاع دایره
- θ: زاویه مقابل کمان بر حسب رادیان
این فرمول، فرم کلی فرمول قبلی است. در صورتی که زاویه بر حسب رادیان داده شد، میتوان به طور مستقیم از این فرمول استفاده کرد. در غیر اینصورت (بیان زاویه به صورت درجه)، باید زاویه را توسط نسبت زیر به شکل رادیان درآورد:
- rad: زاویه بر حسب رادیان
- deg: زاویه بر حسب درجه
- π: عدد ثابت 3/14
عدد پی، نسبت محیط دایره به قطر آن است.
مثال 1: محاسبه طول کمان
طول را حساب کنید.
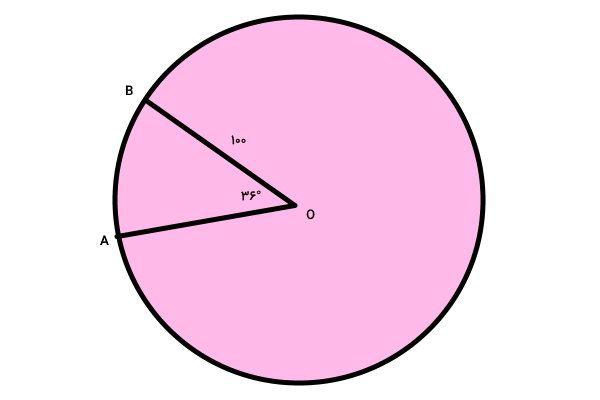
به منظور تعیین طول ، دو راه وجود دارد. در تصویر بالا، شعاع دایره کامل داده شده است. محیط این دایره برابر است با:
شعاع × عدد پی × 2 = محیط دایره کامل
100 × 3/14 × 2 = محیط دایره کامل
628 = محیط دایره کامل
نسبت طول کمان به محیط دایره برابر نسبت زاویه مقابل آن به زاویه دایره کامل است:
بنابراین داریم:
در نتیجه، طول برابر 62/8 است. در روش دوم میتوانستیم اندازه شعاع و زاویه مقابل کمان را به طور مستقیم در فرمول زیر وارد کنیم:
(360 ÷ زاویه کمان) × شعاع × عدد پی × 2 = طول کمان
(360 ÷36) × 100 × 3/14 × 2 = طول کمان
(0/1) × 100 × 3/14 × 2 = طول کمان
10 × 3/14 × 2 = طول کمان
31/4 × 2 = طول کمان
62/8 = طول کمان
مثال 2: محاسبه زاویه کمان
طول یک کمان برابر 56 سانتیمتر و طول دایره کامل برابر 168 سانتیمتر است. زاویه مقابل کمان را حساب کنید.
در این مثال نیز مشابه با مثال 1 میتوانیم زاویه کمان را به دو روش تعیین کنیم. در اینجا، سادهترین روش، تعیین نسبت طول کمان به محیط و استفاده از مقدار به دست آمده است:
3 ÷ 1 = 168 ÷ 56 = نسبت طول کمان به محیط
نسبت طول کمان به محیط دایره برابر یکسوم است. بنابراین، زاویه مقابل کمان نیز یکسوم زاویه دایره (360 درجه تقسیم بر 3) خواهد بود:
120 = 3 ÷ 360 = زاویه کمان
در نتیجه، زاویه مقابل کمان دایره برابر 120 درجه است.
مثال 3: محاسبه طول کمان بر حسب رادیان
اگر زاویه مقابل یک کمان برابر π/4 (پی چهارم) و شعاع دایره کامل برابر 3 باشد، طول کمان بر حسب رادیان چقدر خواهد بود؟
در صورت مسئله، اندازه زاویه بر حسب رادیان داده شده است. از اینرو، به منظور تعیین طول کمان از فرمول آن بر حسب رادیان استفاده میکنیم:
- l: طول کمان
- r: شعاع دایره برابر 3
- θ: زاویه مقابل کمان برابر پی چهارم
مثال 4: محاسبه طول کمان به کمک خواص مماس
مماس دایره، خطی است که با محیط دایره در یک نقطه تلاقی پیدا میکند. در صورت رسم شعاع دایره از نقطه تلاقی، یک زاویه قائمه بین مماس و شعاع دایره تشکیل میشود.
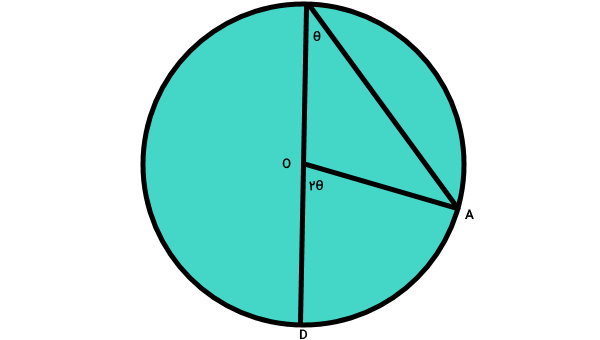
در تصویر زیر، پارهخط AB در نقطه A بر دایره مماس شده است. نقطه O نیز مرکز دایره را نمایش میدهد. با توجه به توضیحات ارائه شده، زاویه کمان AD و طول آن را محاسبه کنید.
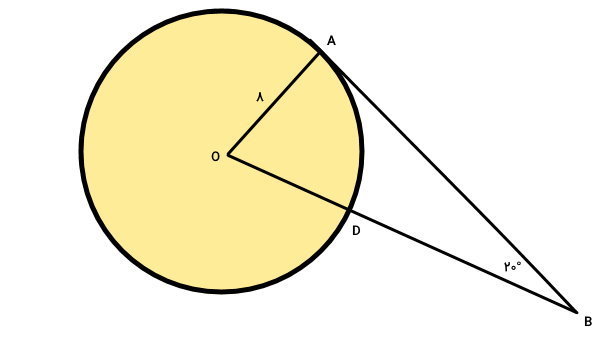
در تصویر بالا، پارهخط AB، مماس دایره و پارهخط OA، شعاع دایره است. طبق تعریف، زاویه بین این دو پارهخط باید 90 درجه باشد.
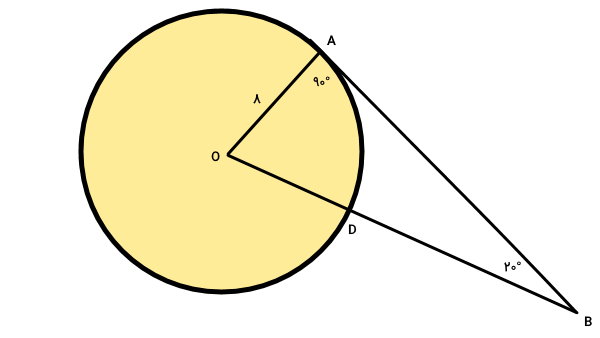
بنابراین، دو زاویه مثلث OAB را داریم. زاویه سوم در راس O، از قانون جمع زوایای داخلی مثلث به دست میآید. مطابق با این قانون، مجموع زوایای داخلی هر مثلث برابر 180 درجه است. به این ترتیب، داریم:
در نتیجه، زاویه راس O یا همان زاویه مقابل به کمان AD برابر 70 درجه است. با داشتن زاویه کمان میتوانیم طول آن را با استفاده از فرمول زیر محاسبه کنیم:
- : طول کمان
- r: شعاع دایره برابر 8
- θ: زاویه مقابل کمان برابر 70 درجه
در نتیجه، طول کمان AD تقریبا برابر 9/77 است.
اجزای مرتبط با کمان دایره چه هستند؟
وتر، قطعه و قطاع دایره، با توجه به مفهوم کمان تعریف میشوند. در ادامه به معرفی این موارد میپردازیم.
وتر دایره چیست؟
به پارهخطی که دو انتهای کمان دایره را به هم وصل میکند، وتر دایره میگویند.
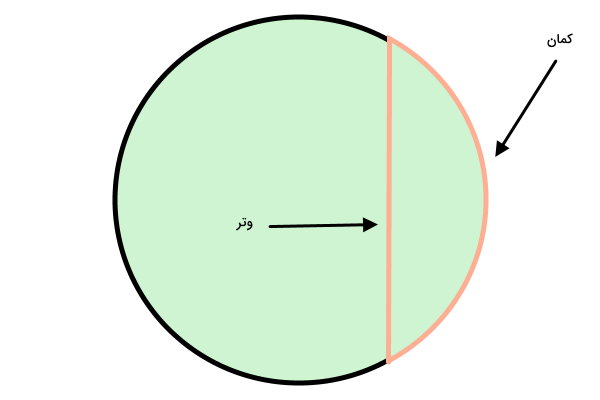
قطعه دایره چیست؟
قطعه دایره، ناحیه محدود به وتر و کمان دایره است. به عنوان مثال، در تصویر زیر، ناحیه سفید، یکی از قطعههای دایره و ناحیه رنگی، قطعه مکمل آن را نمایش میدهد.
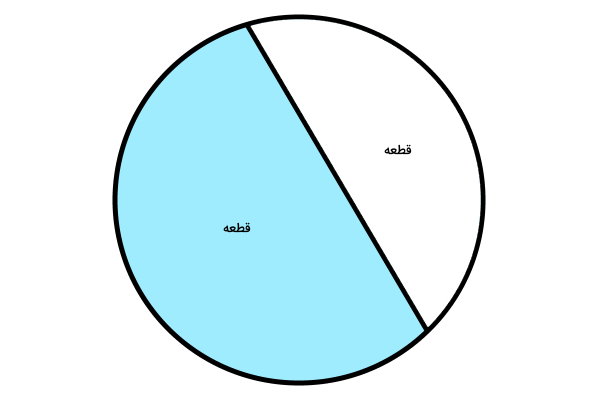
قطاع دایره چیست؟
اگر دو انتهای کمان دایره را به مرکز آن متصل کنیم، دایره به دو قطاع تقسم میشود. قطاع دایره، ناحیه محدود به کمان و دو شعاع آن است. در تصویر زیر، هر دو ناحیه سفید و رنگی، به عنوان قطاعهای دایره در نظر گرفته میشوند.
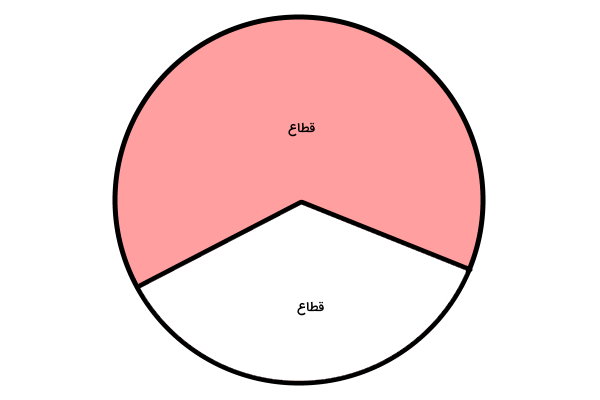
کمان نیم دایره چیست؟
اگر اندازه کمان برابر با نصف محیط دایره باشد، به آن کمان نیمدایره میگویند. در رابطه با محیط و مساحت نیمدایره، دو مطلب در مجله فرادرس تهیه شده است که مطالعه آنها را به شما پیشنهاد میکنیم:
ربعدایره نیز یکی دیگر از انواع قطاعهای دایره است. هر ربعدایره، از یک کمان به طول یکچهارم محیط دایره کامل و دو شعاع تشکیل میشود. برای آشنایی بیشتر با این قطاع، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد میکنیم:
محاسبه آنلاین زاویه و طول کمان دایره
یکی از روشهای محاسبه زاویه و طول کمان دایره، استفاده از سایتهای اینترنتی تخصصی در این زمینه است. به عنوان مثال، ماشین حساب سایت Omni Calculator (+) امکان محاسبه اندازههای طول و زاویه کمان را به همراه مساحت قطاع و طول وتر مقابل کمان را فراهم میکند. تصویر زیر، ماشین حساب کمان در سایت Omni Calculator را نمایش میدهد.
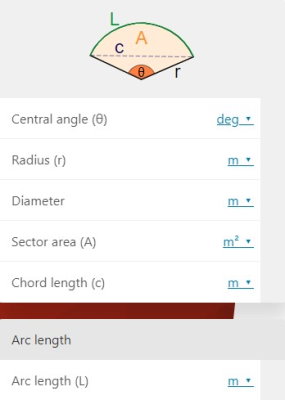
با وارد کردن اندازه زاویه مرکزی (θ) و یکی از اندازههای شعاع، قطر، مساحت قطاع یا طول وتر، طول کمان محاسبه میشود و در کادر مخصوص آن (L) به نمایش در میآید. به عنوان مثال، بر اساس محاسبات این ماشین حساب، طول کمان با زاویه مرکزی 45 درجه و شعاع 19 متر برابر با 14/92 است.
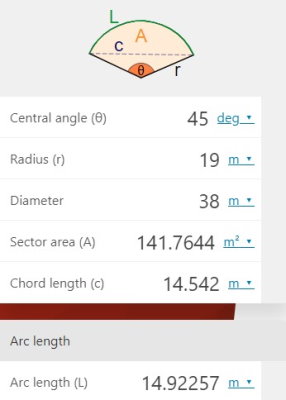
در صورت مشخص بودن اندازه طول کمان و یکی از اندازههای شعاع، قطر یا مساحت قطاع، امکان تعیین زاویه مرکزی کمان نیز فراه میشود. تصویر زیر، محاسبه زاویه کمان با طول 20 متر و شعاع 30 متر را نمایش میدهد.
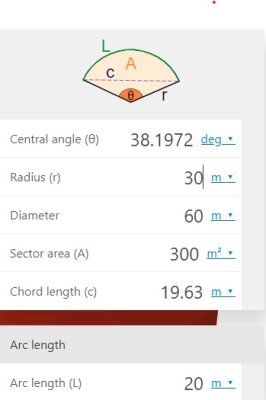
یکی دیگر از ویژگیهای ابزارهای محاسبه آنلاین زاویه و طول کمان دایره، امکان تنظیم واحد تمام اندازههای ورودی و خروجی است. به عنوان مثال، در صورت تمایل میتوانید زاویه را بر حسب رادیان وارد یا محاسبه کنید.
سوالات متداول در رابطه با کمان دایره
در این بخش، به برخی از سوالات پرتکرار در رابطه با کمان دایره، به طور خلاصه پاسخ میدهیم.
تعریف کمان دایره چیست؟
کمان دایره، بخشی از محیط دایره است.
کمان دایره چند درجه است؟
زاویه کمان دایره، زاویه برخورد شعاعهای رسم شده از دو انتهای آن است.
ابزار رسم کمان دایره چیست؟
بهترین ابزار دستی برای رسم کمان دایره، پرگار است.
رابطه بین کمان و وتر دایره چیست؟
وتر، خط اتصالدهنده دو انتهای یک کمان است.
رابطه بین کمان و محیط دایره چیست؟
طول کمان، از ضرب محیط دایره در زاویه مقابل کمان (بر حسب رادیان) به دست میآید.
تفاوت کمان با قطاع چیست؟
کمان دایره، بخشی از محیط دایره است. قطاع، بخشی متشکل از کمان و دو شعاع دایره است.
تفاوت زاویه مرکزی و محاطی دایره چیست؟
راس زاویه مرکزی دایره بر روی مرکز آن قرار میگیرد؛ در صورتیکه راس زاویه محاطی دایره بر روی محیط آن قرار دارد.
شباهت زاویه مرکزی و محاطی دایره چیست؟
هر دو زاویه مرکزی و محاطی، محدود به محیط دایره (روی محیط یا درون آن) هستند.
کدام دو نقطه دایره را به دو کمان مساوی تقسیم میکنند؟
نقاط ابتدا و انتهای هر قطر، دایره را به دو کمان مساوی تقسیم میکنند.
آزمون کمان دایره
۱. کدام عبارت ماهیت دقیق منحنی کمان دایره (Arc) را طبق تعریف استاندارد هندسی بیان میکند؟
بخشی از محیط دایره که بین دو نقطه روی آن قرار دارد.
پارهخطی که دو نقطه روی محیط دایره را به هم وصل میکند.
نقطهای روی محیط دایره که به مرکز متصل شده است.
ناحیهای از دایره بین دو شعاع و محیط دایره.
عبارت «بخشی از محیط دایره که بین دو نقطه روی آن قرار دارد» تعریف هندسی استاندارد کمان دایره (Arc) است. این بخش از محیط، منحنی بین دو نقطه روی محیط دایره محسوب میشود.
۲. در ریاضیات، برای نمایش آرک بین دو نقطه A و B روی محیط دایره از چه نشانهای معمولا استفاده میشود؟
دو نقطه کنار هم بدون نشانه خاصی نوشته میشوند.
علامت قوسیشکل بالای AB مانند ⌒ یا به کار میرود.
خط راست بالای AB قرار میگیرد.
نماد دایره کوچک کنار AB قرار داده میشود.
در نمایش ریاضی کمان یا آرک میان دو نقطه روی دایره، از علامت قوسیشکل در بالای نام نقاط استفاده میشود. این روش نوشتاری به صورت ⌒ یا کاملا متداول است تا کمان را از سایر اجزا متمایز کند.
۳. کدام عبارت به صورت صحیح فرمول طول کمان، رابطه آن با زاویه مرکزی و شعاع دایره و واحدهای متداول ارتباطی را بیان میکند؟
رابطه طول کمان با زاویه مرکزی فقط در صورتی برقرار است که شعاع یک واحد فرض شود و طول کمان بدون واحد بیان میگردد.
طول کمان فقط به اندازه وتر و محیط دایره بستگی دارد و معمولا با واحد درجه محاسبه میشود.
برای محاسبه طول کمان فقط زاویه مرکزی به رادیان نیاز است و واحد حاصل زاویه (رادیان یا درجه) است.
طول کمان برابر شعاع ضربدر زاویه مرکزی بر حسب رادیان است و خروجی با واحد طول مانند سانتیمتر یا متر بیان میشود.
فرمول صحیح برای طول کمان این است که طول کمان حاصل ضرب شعاع در زاویه مرکزی بر حسب رادیان است. مقدار به دست آمده همیشه با یکای طول (مثلا سانتیمتر یا متر) سنجیده میشود.
۴. وقتی سه نقطه A، B و C روی محیط دایره قرار دارند و C بین A و B است، چه روشی برای تشخیص و نامگذاری کمان کوچک و بزرگ بین A و B کاربرد دارد؟
کمان کوچک بین A و B، کوتاهترین مسافت روی محیط بین این دو نقطه است که از C عبور میکند.
کمان بزرگ بین A و B، بخشی از محیط دایره است که C بین A و B قرار ندارد.
کمان کوچک بین A و B، کمانی است که C بین این دو نقطه قرار گیرد و طول کمتری نسبت به کمان دیگر داشته باشد.
برای تشخیص کمان کوچک، باید هر دو نقطه را با خط راست به هم وصل کنیم و کمانی که تقسیم کوچکتری دارد همان کمان کوچک است.
کمان کوچک میان دو نقطه A و B آن بخشی از محیط دایره است که نقطه C بین آن دو قرار گیرد و این کمان نسبت به کمان دیگر کوتاهتر است.
۵. دانشآموز برای پیداکردن طول کمان در دایرهای با شعاع ۶ سانتیمتر و زاویه مرکزی ۴۵ درجه، کدام مراحل و فرمول را دنبال کند؟
فرمول محیط کامل و تقسیم بر ۸ برای طول کمان، بدون نیاز به رادیان
فرمول l = r θ با تبدیل ۴۵ درجه به رادیان، سپس ضرب در شعاع
فرمول l = r θ با زاویه به درجه بدون تبدیل، سپس تقسیم بر محیط
فقط محاسبه نسبت ۴۵ به ۱۸۰ و ضرب در محیط دایره
برای محاسبه طول کمان زمانی که زاویه مرکزی به درجه داده شده، ابتدا باید زاویه را به رادیان تبدیل کرد. سپس از فرمول l = r θ استفاده میشود، به این صورت که ابتدا ۴۵ درجه را به رادیان (۴۵ × π / ۱۸۰) تبدیل میکنند، سپس مقدار به دست آمده در شعاع (۶ سانتیمتر) ضرب میشود تا طول کمان به دست آید.
۶. اگر در یک دایره دو کمان برابر داشته باشیم، کدام یک از ویژگیهای زیر درباره وتر، زاویه مرکزی و زاویه محاطی مقابل این کمانها صحیح است؟
هیچ ارتباط مستقیمی بین طول وتر و زاویه کمانهای برابر وجود ندارد.
وترهای مقابل دو کمان برابر همیشه مساویاند و زوایای مرکزی نیز برابر خواهند بود.
زاویه محاطی رو به کمانهای برابر همیشه بزرگتر است ولی وترها برابر نیستند.
فقط زاویه مرکزی کمانها برابر است اما وترها ممکن است متفاوت باشند.
وقتی دو کمان برابر روی یک دایره باشند، وترهای مقابل دو کمان دقیقا طول مساوی خواهند داشت. همچنین، زاویه مرکزی روبروی هر یک از این دو کمان نیز به دلیل برابری طول کمانها کاملا برابر است. به همین صورت، زاویه محاطی مقابل آن کمانها نیز اندازه کاملا یکسانی دارد.به عبارت دیگر، برابری کمانها سبب برابری طول وتر مقابل و همچنین زوایای مربوطه (مرکزی و محاطی) میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت دایره + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- دایره چیست ؟ — تعریف و مفاهیم به زبان ساده
- شعاع چیست ؟ — شعاع دایره به زبان ساده
- وتر چیست ؟ — به زبان ساده
- عدد پی (Π) چیست ؟ — کاربردها به زبان ساده
- قطاع و مقطع دایره و محاسبات آن در هندسه — به زبان ساده
- محیط دایره به زبان ساده + حل تمرین و فیلم آموزش رایگان
- مساحت دایره به زبان ساده + حل تمرین
- فرمول محیط دایره چیست ؟ + حل تمرین و مثال
- فرمول مساحت دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- نسبت محیط دایره به قطر آن چیست ؟ — به زبان ساده
- نسبت محیط دایره به شعاع آن چیست ؟ — به زبان ساده
- مساحت نیم دایره چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- مساحت ربع دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محاسبه محیط دایره آنلاین — بهترین سایت ها + حل تمرین
- محیط نیم دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط ربع دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محاسبه گر مساحت دایره آنلاین — بهترین سایت ها + حل تمرین و مثال
- محیط و مساحت دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط دایره با چی متناسب است ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط و مساحت دایره چیست ؟ — به زبان ساده + حل مثال
- دایره چند شعاع دارد ؟ — تصویری و به زبان ساده
- مماس دایره چیست و چه ویژگی هایی دارد؟ — به زبان ساده + حل تمرین و مثال
- کمان دایره چیست ؟ — محاسبه طول و اندازه + حل مثال(همین مطلب)
- قطر دایره چیست ؟ — رسم و محاسبه قطر + حل تمرین و مثال
- قطعه دایره چیست ؟ — فرمول محیط و مساحت + حل مثال
- قطاع دایره چیست ؟ — فرمول های محاسبه محیط و مساحت + حل مثال و تمرین













سلام
برای محاسبه طول کمان در نیم دایره باید چکار کرد؟
سلام
با تشکر از بحث آموزنده
لطفا در انتهای مطلب
(زاویه کمان دایره چیست ؟) عبارت طول کمان AB از طول کمان CD بزرگتر است، را
اصلاح بفرمایید
(طول کمان CD از طول کمان AB بزرگتر است) صحیح است
با احترام
سلامی
با سلام و وقت بخیر؛
ممنون از دقت نظر شما. متن اصلاح شد.
با عرض سلام، یک سوال دارم خدمت اساتید محترم و آن اینکه آیا در فرمول جاذبه نیوتن برای محاسبه نیروی گرانش بین دو جرم ، مقدار R یعنی فاصله بین مراکز ثقل آن دو جرم برابر با وتر و یا کمان در نظر گرفته می شود؟ پیشاپیش سپاسگزارم.
سلام وقتی طول و محیط و هیچی دایره رو بهمون ندادن و فقط گفتن دایره ای مثلا به هشت کمان مساوی تقسیم شده چجوری باید اندازه ی کمان هارو محاسبه کنیم؟
با سلام؛
مقدار R در رابطه نیروی گرانش فاصله مرکزهای جرم دو جسم از یکدیگر است،
با تشکر از همراهس شما با مجله فرادرس
من یه سوال ساده داشتم که به همه مسائل اشاره شد بجز سوال من
سلام.وقت بخیر.ضمن تشکر از مطالب عالی شما.سوال دارم .اگردر قطعه دایره ، طول وتر دایره معلوم باشد و طول عمود بر وتر ،چگونه باید طول کمان حساب کنیم