کشش نخ – به زبان ساده

یکی از مباحث مهم در فیزیک و مکانیک کلاسیک، نیروی کشش نخ یا طناب است. کشش نخ نیرویی است که توسط یک نخ، طناب، کابل، سیم یا موارد مشابه به یک یا چند جسم وارد میشود. هر جسمی که به ریسمانی آویزان شده باشد یا توسط طنابی بچرخد یا همانند آونگ، حرکتی رفت و برگشتی انجام دهد، نیروی کشش نخ به آن اعمال میشود.
محاسبه نیروی کشش نخ نهتنها برای رشتههای فیزیک و مکانیک، بلکه برای مهندسان عمران و معمارانی که به وفور از طناب در پروژههای خود از آن استفاده میکنند نیز اهمیت بسیار زیادی دارد. در این مقاله قصد داریم تا به زبانی ساده به بررسی نیروی کشش نخ و نحوه محاسبه آن در مثالهای متنوع بپردازیم. با ما در ادامه این مقاله همراه باشید.
نیروی کشش نخ
در این قسمت به محاسبه نیروی کشش یک رشته نخ میپردازیم. در بخش بعدی به بررسی سیستم چند رشتهای خواهیم پرداخت. در اینجا نخ یا طنابهایی بررسی میشوند که به صورت یکنواخت کشیده میشوند. در واقع نیروی کشش نخ به هر جزء از طناب به طور یکسان وارد میشود.
محاسبه نیروی وزن (گرانش)
کشش در یک رشته نخ، ریسمان یا موارد مشابه، نتیجه نیرویی است که از هر دو طرف (انتها) به ریسمان وارد میشود. از قانون دوم نیوتن به یاد داریم که نیرو، حاصل ضرب جرم در شتاب است که با واحد نیوتن سنجیده میشود.
در صورتی که طناب محکم کشیده شده باشد، هرگونه تغییر در شتاب یا جرم اجسام متصل به طناب، در نیروی کشش نخ تغییر ایجاد میکند. یادآور میشویم که طناب مد نظر ما، جرمی یکنواخت در واحد طول داشته و میزان کشیده شدنش در هر جزء یکسان است. همچنین از جرم طناب در محاسبات صرفنظر میکنیم. نکتهای که در اینجا باید به یاد داشته باشید، فراموش نکردن شتاب گرانش زمین ()، برای اجسام متصل به طناب است. پس برای حالتی که یک جسم از طریق طنابی آویزان و در حال تعادل است، نیروی کشش نخ برابر با نیروی وزن است. به شکل زیر دقت کنید.

برابری نیروی کشش نخ و نیرو وزن از قانون سوم نیوتن نتیجه میشود. احتمالاً عبارت «هر عملی، عکسالعملی است برابر و در خلاف جهت» را زیاد شنیدهاید. عبارت مذکور بیان قانون سوم نیوتن بوده و مطابق با آن نیرو وزن در جهت پایین و نیرو کشش نخ در جهت بالا است.
حال فرض کنید که میخواهیم جسم 10 کیلوگرمی شکل فوق را توسط طنابی با شتاب ثابت به سمت بالا ببریم. به نظر شما چه میزان نیروی کشش به طناب اعمال میشود؟ در شکل فوق دیدیم که نیرویی از سمت وزن جسم به طناب وارد میشود. حال در شکل زیر مشخص است که نیروی دوم، حاصل شتاب دادن سیستم به طرف بالاست.

پس در مجموع به هنگام حرکت سیستم شکل فوق با شتاب ثابت به طرف بالا، نیروی کشش به طناب وارد میشود.
محاسبه نیروی حاصل از دوران
آونگی را در نظر بگیرید. جسمی که از انتهای طنابی آویزان و حرکت نوسانی (رفتوبرگشت) انجام میدهد یا میچرخد، از طریق نیروس گریز از مرکز (Centrifugal Force) باعث ایجاد نیروd کشش در نخ میشود. برای آشنایی با نیروd گریز از مرکز به مطلب «حرکت دایرهای -- به زبان ساده» مراجعه کنید. میدانیم که نیروd گریز از مرکز مطابق با رابطه زیر محاسبه میشود.
مطابق رابطه فوق، هر چه جرم و سرعت چرخش جسم بیشتر باشد، نیروی گریز از مرکز بیشتر است. در رابطه فوق شعاع دایرهای است که روی محیط آن حرکت دایرهای انجام میگیرد. در اینجا شعاع همان طول طناب است. در ادامه در نظر داریم تا نیرو کشش نخ برای یک حرکت آونگی را محاسبه کنیم. از آنجا که جهت و بزرگی نیروی گریز از مرکز با تغییر مکان جسم، در واقع تغییر سرعت، تغییر میکند، میخواهیم بیشترین نیروی کشش نخ را در حرکت مذکور به دست آوریم. در این حرکت، جسم در نقطه تعادل آونگ بیشترین سرعت را دارد. همچنین به یاد داشته باشید که نیروی گرانش (وزن) همیشه به سمت پایین بر جسم اثر میکند.
حال حرکت نوسانی آونگی را در نظر بگیرید که سرعت جسم 10 کیلوگرمی در پایینترین نقطه (نقطه تعادل آونگ) است. طول طناب آونگ را در نظر بگیرید. نیروی کشش نخ به صورت زیر محاسبه میشود:
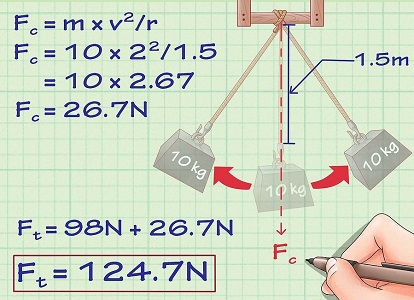
در حالت فوق، یعنی لحظهای که جسم در پایینترین نقطه قرار دارد. نیروی وزن همانند حالتی محاسبه میشود که سیستم جسم و طناب در حال تعادل هستند. پیشتر بیان کردیم که نیروی وزن همیشه به سمت پایین است. حال اگر در نقطهای به جز نقطه تعادل آونگ در حرکت دایرهای، اقدام به محاسبه نیروی کشش نخ کنیم، تاثیر نیروی وزن بر کشش نخ متفاوت خواهد بود. در این حالت نیروی کشش نخ، که در واقع عکسالعمل نیروی وزن است، برابر با بخشی () از این نیرو است. در واقع () مولفهای است که در راستا (موازات) نیروی کششی طناب است. این مطلب را در قالب مثال زیر عنوان میکنیم.
دوباره حرکت آونگی را در نظر بگیرید. به عنوان مثال میخواهیم نیروی کشش طناب را در حالتی که نسبت به وضعیت تعادل، به اندازه ۱۵ درجه به طرف چپ یا راست رفته است، محاسبه کنیم. در این نقطه سرعت جسم است. در نتیجه نیروی کشش طناب به صورت زیر است:

همانطور که در شکل فوق مشاهده میشود، نیروی کشش نخ در این نقطه مقدار کمتری نسبت به پایینترین نقطه دارد. اگر برایتان سوال است که چرا مقدار () در کسینوس زاویه ضرب شده است، به مقاله «بردار - به زبان ساده» مراجعه کنید. حال به نظر شما به هنگام چرخاندن جسمی از طریق طناب، در کدام نقطه از حرکت دایرهای احتمال پاره شدن طناب بیشتر است؟
نیروی کشش نخ حاصل از نیرو اصطکاک
در این قسمت میخواهیم نیروی کشش ناشی از اصطکاک را محاسبه کنیم. فرض کنید که به جسمی ۱۰ کیلوگرمی طنابی بسته و آن را از طریق طناب روی زمین میکشیم. در مقاله «اصطکاک — به زبان ساده» دیدیم که به هنگام حرکت یک جسم از حال سکون، با دو نوع نیروی اصطکاک روبهرو هستیم.
مورد اول، نیروی اصطکاکی است که مانع از حرکت جسم میشود. این نیروی اصطکاک به اصطکاک ایستایی موسوم بوده که طبق رابطه محاسبه میشود. مورد دوم، اصطکاک جنبشی () است که همیشه مقداری کمتر از اصطکاک ایستایی دارد (). اگر دقت کرده باشید به هنگام هل دادن یک جسم، در ابتدا نیروی بیشتری باید صرف کنید، اما به محض اینکه جسم شروع به حرکت کرد، نیروی کمتری برای هل دادن آن نیاز است، علت این امر در نهفته است. در دو رابطه نیروی اصطکاک ایستایی و جنبشی، نیروی عمودی سطح (تکیهگاه) بوده که برابر با نیرو وزن است. به طور مثال به هنگام کشیدن جسمی ۱۰ کیلوگرمی به وسیله طناب، روی سطحی که ضریب اصطکاک جنبشی آن 0.5 است، نیروی کشش نخ به صورت شکل زیر محاسبه میشود:

حال اگر فرض کنیم که ضریب اصطکاک ایستایی سطح برای جسم ۰/۷ باشد، نیروی اصطکاک آن به صورت زیر محاسبه میشود:
در اینجا حداقل نیروی کششی نخ جهت حرکت جسم (آستانه حرکت)، باید برابر با باشد. اما به محض حرکت، اصطکاک جنبشی وارد عمل شده و حداقل نیرو برای کشیدن جسم توسط طناب (حرکت با شتاب صفر یا همان سرعت ثابت) به کاهش پیدا میکند.
محاسبه کشش نخ در حالتهای چندتایی
در این بخش میخواهیم نیروی کشش نخ را در سیستمهایی بررسی کنیم که بتوان آنها را متشکل از چند ریسمان در نظر گرفت. به حالتهایی که در زیر آمده است توجه کنید.
نیروی کشش نخ در قرقره
قرقره را میتوان ماشینی ساده، متشکل از دیسکی معلق (آویزان) در نظر گرفت که سبب تغییر جهت نیروی کششی در طناب میشود.
در ساختار طناب و قرقره، دو جسم به دو انتهای طناب بسته شدهاند. اگر یکی از جسمها سنگینتر باشد، به سمت پایین حرکت کرده و در نتیجه جسم سبکتر به سمت بالا میرود. در واقع میتوان گفت که طول طناب در دوطرف قرقره تغییر میکند. در اینجا نیز جهت سادگی کار، از جرم قرقره و طناب صرفنظر میکنیم. همچنین حرکت طناب روی قرقره اصطکاکی ندارد. همانند حالتهای قبلی ساختار طناب، یکنواخت و نیروی کششی به هر جزء آن به صورت یکسان وارد میشود.
با این اوصاف، مطابق با قانون سوم نیوتن، نیروی کشش نخ در دو انتهای ریسمان، حتی اگر توسط نیروهای متفاوت وزن کشیده شوند، برابر است. برای این سیستم ساده، نیروی کشش نخ برابر با مقدار زیر است:
به طور مثال جسمی ۱۰ کیلوگرمی و جسمی ۵ کیلوگرمی را از دو انتهای طناب قرقره آویزان میکنیم. نیروی کشش نخ به صورت زیر محاسبه میشود:

دقت شود از آنجایی که نیروی کشش نخ در همهجا یکسان است، شتاب کل سیستم نیز ثابت است.
در مثال فوق، طنابهای دو سمت قرقره با یکدیگر موازی بودند. حال در مثال زیر فرض میکنیم که دو طناب موازی نبوده و راستای یکی از طنابها با سطح افقی زاویه درجه میسازد. میتوانید فرض کنیم که قرقره بالای سطحی شیبدار، به شکل زیر قرار دارد.
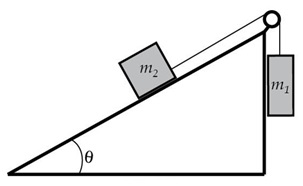
مطابق شکل فوق، جرم ۱۰ کیلوگرمی را جسم و جرم ۵ کیلوگرمی را جسم فرض میکنیم. فرض کنید که جسم با سطح شیبدار بدون اصطکاک است. نیروی کشش نخ در این حالت به صورت زیر محاسبه میشود:
جسم ۱۰ کیلوگرمی که آویزان است، به سمت پایین حرکت میکند. پس نیرویی که عامل شتاب آن میشود برابر است با:
در خصوص جسم دوم، بخشی از نیروی وزن در راستای کشش نخ قرار میگیرد. در واقع نیروی در خلاف جهت نیروی کشش نخ اعمال میشود. پس نیرویی که باعث شتاب دادن جسم میشود به صورت زیر است:
از آنجایی که نیروی کششی طناب به هر جزء از آن به صورت یکسان وارد میشود، شتاب کل سیستم ثابت و یکسان است. در واقع شتاب حرکت جسم و برابر است. در نتیجه از رابطه داریم:
در اینجا نیز اگر برایتان سوال است که چرا نیروی وزن () را در سینوس زاویه سطح شیبدار ضرب کردیم، به مقاله «سطح شیبدار -- به زبان ساده» رجوع کنید.
نگه داشتن یک جسم توسط چند ریسمان
در این بخش در نظر داریم تا نیروی کشش نخ را در سیستمی «Y» شکل بررسی کنیم. مطابق با شکل زیر، وزنهای ۱۰ کیلوگرمی توسط طنابهایی به شکل «Y» در حال تعادل است. نیروی کشش در طناب پایین مشخص و برابر با نیروی وزن حاصل از جرم ۱۰ کیلوگرمی است. از آنجایی که سیستم در حال تعادل است، باید مجموع مولفههای عمودی طنابهای و با نیروی وزن (کشش طناب پایین) برابر باشد. همچنین مولفههای افقی دو طناب و باید برابر باشند تا تعادل سیستم حفظ شود. با توجه به توضیحات فوق، برای محاسبه نیروی کشش طناب در سیستم مذکور به شرح زیر عمل میکنیم:
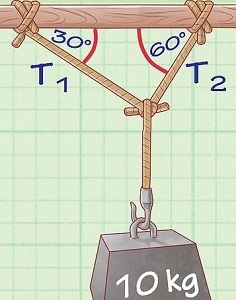
میدانیم که نیروی گرانش (وزن) به سمت پایین است. در نظر بگیرید که نیروی وزن جسم ۱۰ کیلوگرمی به مرکز سیستم Y، یعنی جایی که سه طناب به یکدیگر گره خوردهاند، وارد میشود. اجازه دهید طنابی که در راستای عمود قرار دارد را بنامیم. مشخص است که نیروی کشش نخ به سادگی برابر با نیروی وزن است. اما همانطور که در مثالهای قبلی دیدیم، در صورتی که طنابها نسبت به حالت عمود، دارای زاویه باشند، تنها بخشی از نیروی وزن در راستای آنها قرار میگیرد. در نتیجه داریم:
گفتیم که سیستم در حال تعادل است، پس تمامی نیروهای موجود در سیستم در دو راستای عمودی و افقی باید یکدیگر را خنثی کنند. برای بررسی درستی پاسخ به شکل زیر دقت کنید:
در راستای عمودی داریم:
رابطه (۱)
و در راستای افقی:
رابطه (۲)
دو معادله و دو مجهول داریم. با استفاده از رابطه (۲)، کشش نخ در طناب یک را بر حسب کشش نخ در طناب ۲ بهدست میآوریم و آن را در رابطه (۱) قرار میدهیم. به این ترتیب،کشش نخ ۱ برابر ۴۹ نیوتن و کشش نخ ۲ برابر ۸۴/۵ نیوتن خواهند بود.
همانطور که ملاحظه میشود تمامی نیروهای درگیر در سیستم یکدیگر را خنثی کرده و سیستم در حال تعادل است. در واقع هیچ نیرویی وجود ندارد که باعث شتاب دادن جسم شود.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- آموزش فیزیک پایه ۱
- مجموعه آموزشهای مهندسی مکانیک
- حرکت سقوط آزاد -- به زبان ساده
- حرکت با شتاب ثابت -- به زبان ساده
- معادله دیفرانسیل حرکت — از صفر تا صد
- اصطکاک — به زبان ساده
^^













سلام در مسعله آخر جای T چی میزاریم
بهتر است نویسنده محترم یک بار دیگر خودش مقاله را مطالعه نموده و اشکالات نگارشی آن را اصلاح نمایند.
به عنوان مثال عبارت: “نیرو کشش نخ حاصل از نیرو اصطکاک” درست نیست. درست آن به شکل زیر است:
نیروی کشش نخ حاصل از نیروی اصطکاک
اشکالات نگارشی از این نوع فراوان و مکرر در متن دیده میشود؛ مانند:
محاسبه نیرو وزن؛ محاسبه نیرو حاصل از دوران؛ محاسبه نیرو کشش نخ؛ نیرو گریز از مرکز و …
که در همهی عبارتهای بالا حرف “ی” افتاده است.
در ضمن نیروی گریز از مرکز به انگلیسی centrifugal force میشود، که به اشتباه Centripetal Force نوشته شده است. معنی عبارت اخیر نیروی متمایل به مرکز است نه گریز از مرکز.
با سلام؛
متن بازبینی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس
hello. That’s nice but I wish you would put the site in English so that I don’t have to use transliteration.
این مسله آخر اشتباه حل شد کاملا اشتباهه تو این مساله باید تجزیه کرد
با سلام،
مساله آخر ویرایش و اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس