پیاده سازی توزیع های احتمال در پایتون — راهنمای کاربردی

در این مطلب، چهار «توزیع احتمال» (Probability Distribution) محبوب، شامل «توزیع لاگ نرمال» (Log-Normal Distribution)، «توزیع دوجمله‌ای» (Binomial Distribution)، «توزیع پواسون» (Poisson Distribution) و «توزیع برنولی» (Bernoulli Distribution) به طور مختصر معرفی شده‌اند. سپس، روش پیاده‌سازی این توزیع های احتمال در پایتون شرح داده شده است.

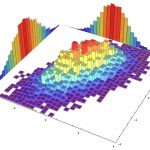
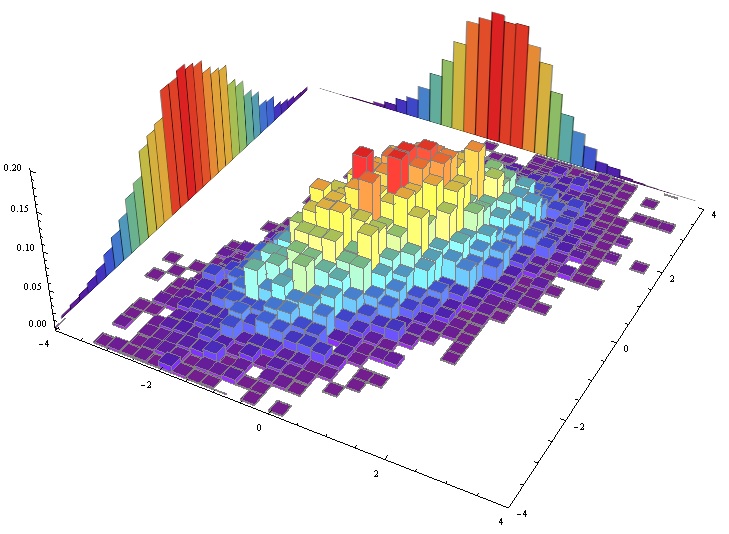
توزیع لاگ نرمال

در تئوری آمار و احتمال، توزیع «لاگ نرمال» (Log-normal) به عنوان یک توزیع پیوسته، برای بیان رفتار بعضی از پدیده‌های احتمالی، به کار می‌رود. اگر متغیر تصادفی $$X$$ دارای توزیع لاگ نرمال باشد، آنگاه توزیع $$Y=ln\left(X\right)$$ نرمال است. به همین ترتیب می‌توان گفت، اگر $$Y$$ توزیع نرمال داشته باشد، آنگاه $$X=\mathrm{EXP}\left(Y\right)$$ دارای توزیع «لاگ نرمال» است.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

در ادامه، از کتابخانه پایتون «نام‌پای» (NumPy) برای پیاده‌سازی این توزیع استفاده شده است.

1>>> import scipy.stats
2>>> import numpy as np
3>>> import matplotlib.pyplot as plt
4>>> np.random.seed(1234)
5>>> samples=np.random.lognormal(mean=1.,sigma=.4,size=10000)
6>>> shape,loc,scale=scipy.stats.lognorm.fit(samples,floc=0)
7>>> num_bins=50
8>>> clr="#EFEFEF"
9>>> counts,edges,patches=plt.hist(samples,bins=num_bins,color=clr)
10>>> centers=0.5*(edges[:-1]+edges[1:])
11>>> cdf=scipy.stats.lognorm.cdf(edges,shape,loc=loc,scale=scale)
12>>> prob=np.diff(cdf)
13>>> plt.plot(centers,samples.size*prob,'k-',linewidth=2)

1[<matplotlib.lines.Line2D object at 0x0359E890>]

1>>> plt.show()

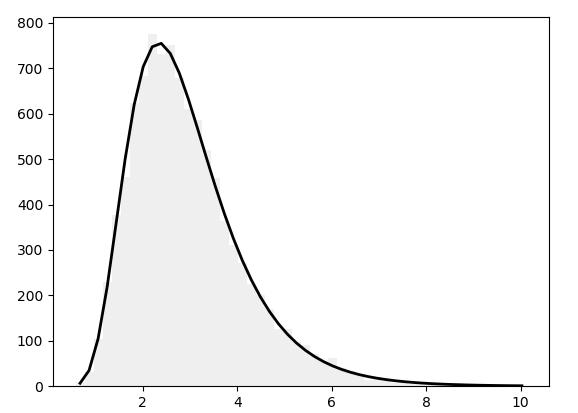
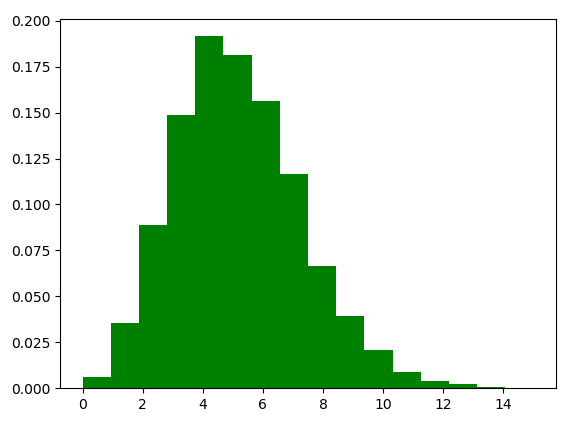
توزیع دوجمله‌ای

توزیع دوجمله‌ای، احتمال موفقیت در n آزمایش مستقل را تعیین می‌کند. این آزمایش‌ها، پرسش‌های بله-خیر هستند. یکی از مثال‌های معروف توزیع دوجمله‌ای، پرتاب سکه است.

فیلم آموزش ریاضی برای یادگیری ماشین + پیاده سازی در پایتون در فرادرس

کلیک کنید

در ادامه، کد پیاده‌سازی این توزیع در زبان برنامه‌نویسی پایتون با بهره‌گیری از کتابخانه‌های Seaborn ارائه شده است.

1>>> import seaborn
2>>> from scipy.stats import binom
3>>> data=binom.rvs(n=17,p=0.7,loc=0,size=1010)
4>>> ax=seaborn.distplot(data,
5                kde=True,
6                color='pink',
7                hist_kws={"linewidth": 22,'alpha':0.77})
8>>> ax.set(xlabel='Binomial',ylabel='Frequency')

1[Text(0,0.5,’Frequency’), Text(0.5,0,’Binomial’)]

1>>> plt.show()

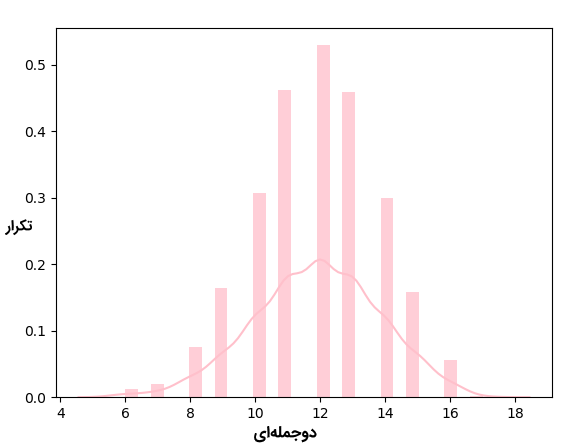
مثال دیگری از توزیع دوجمله‌ای که با استفاده از کتابخانه NumPy پیاده‌سازی شده، در زیر آمده است.

1>>> s=np.random.binomial(10,0.5,1000)
2>>> plt.hist(s,16,normed=True,color='Brown')

(array([0.00177778, 0.02311111, 0. , 0.08711111, 0. ,
0.18666667, 0. , 0.33777778, 0.45155556, 0. ,
0.37688889, 0. , 0.224 , 0. , 0.07466667,
0.01422222]), array([0. , 0.5625, 1.125 , 1.6875, 2.25 , 2.8125, 3.375 , 3.9375,
4.5 , 5.0625, 5.625 , 6.1875, 6.75 , 7.3125, 7.875 , 8.4375,
9. ]), 

1>>> plt.show()

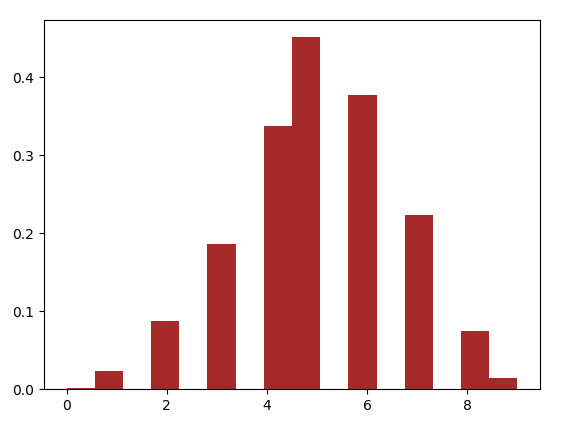
توزیع پواسون در پایتون

توزیع پواسون، احتمال وقوع تعداد مشخصی از رویدادها در یک بازه ثابت از زمان یا فضا را فراهم می‌کند.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

این توزیع، فرض می‌کند که رویدادها با نرخ ثابتی به وقوع می‌پیوندند و هر رویداد، مستقل از رویداد پیش از خود است.

1>>> import numpy as np
2>>> s=np.random.poisson(5, 10000)
3>>> import matplotlib.pyplot as plt
4>>> plt.hist(s,16,normed=True,color='Green')

1(array([5.86666667e-03, 3.55200000e-02, 8.86400000e-02, 1.48906667e-01,
21.91573333e-01, 1.81440000e-01, 1.56160000e-01, 1.16586667e-01,
36.65600000e-02, 3.90400000e-02, 2.06933333e-02, 9.06666667e-03,
43.84000000e-03, 2.13333333e-03, 5.33333333e-04, 1.06666667e-04]), array([ 0. , 0.9375, 1.875 , 2.8125, 3.75 , 4.6875, 5.625 ,
56.5625, 7.5 , 8.4375, 9.375 , 10.3125, 11.25 , 12.1875,
613.125 , 14.0625, 15. ]), <a list of 16 Patch objects>)

1>>> plt.show()

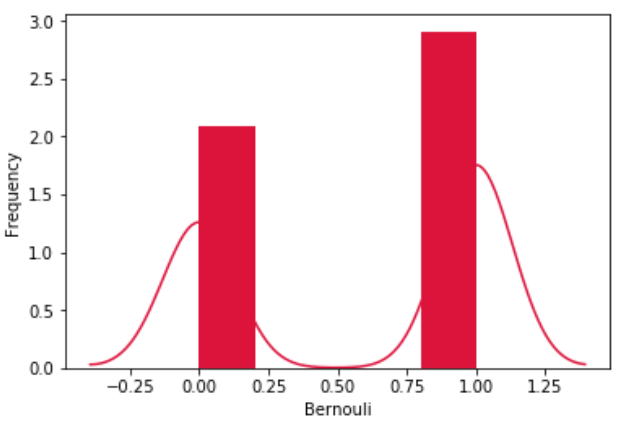
توزیع برنولی

توزیع برنولی، نوعی از توزیع دوجمله‌ای است که در آن یک آزمایش یکتا انجام می‌شود. این توزیع، یک توزیع احتمال گسسته است که احتمال p را برای مقدار ۱ و احتمال q را برای مقدار ۰ دارد. p می‌تواند «موفقیت» (Success)، «بله» (Yes)، «درست» (True) یا یک باشد.

فیلم آموزش برنامه نویسی R و نرم افزار RStudio – مقدماتی در فرادرس

کلیک کنید

به طور مشابه، q=1-p می‌تواند «شکست» (Failure)، خیر (No)، «غلط» (False) یا صفر باشد. در ادامه، کد پیاده‌سازی توزیع برنولی با استفاده از کتابخانه پایتون «سای‌پای» (scipy) انجام شده است.

1from scipy.stats import bernoulli
2import seaborn as sb
3
4data_bern = bernoulli.rvs(size=1000,p=0.6)
5ax = sb.distplot(data_bern,
6                  kde=True,
7                  color='crimson',
8                  hist_kws={"linewidth": 25,'alpha':1})
9ax.set(xlabel='Bernouli', ylabel='Frequency')

نتیجه‌گیری

در این مطلب، روش پیاده‌سازی توزیع های احتمال در پایتون برای چهار توزیع محبوب لاگ نرمال، دو جمله‌ای، پواسون و برنولی بیان شد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• گنجینه آموزش‌های برنامه نویسی پایتون (Python)
• مجموعه آموزش‌های نرم‌افزارهای آماری
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
• دادهکاوی (Data Mining) — از صفر تا صد