کتابخانه NumPy پایتون – راهنمای جامع — بخش اول

NumPy یک کتابخانه برای زبان برنامه نویسی پایتون (Python) است. با استفاده از این کتابخانه امکان استفاده از آرایهها و ماتریسهای بزرگ چند بعدی فراهم میشود. همچنین میتوان از تابعهای ریاضیاتی سطح بالا بر روی این آرایهها استفاده کرد. پیش از اینکه این آموزش را مطالعه کنید، میبایست دستکم اندکی با زبان برنامهنویسی پایتون آشنایی داشته باشید. همچنین اگر نیاز دارید معلوماتتان را در مورد پایتون یکبار یادآوری کنید، میتوانید از آموزش پایتون استفاده کنید.
همچنین اگر میخواهید بر روی نمونههای ارائه شده در این آموزش کار کنید، باید برخی نرمافزارها را روی رایانه خود نصب کنید. دستکم موارد زیر الزامی هستند.
این نرمافزارها هم مفید هستند.
- ipython یک پوسته (Shell) تعاملی بهبود یافته برای پایتون است که برای بررسی خصوصیات NumPy بسیار مناسب است.
- matplotlib به شما امکان رسم نمودار را میدهد.
- SciPy بسیاری از رویههای علمی را در خود دارد که بر روی NumPy عمل میکنند.

مفاهیم پایه
هدف اصلی NumPy فراهم ساختن امکان کار با آرایههای چندبعدی همگن است. این آرایهها جدولی از عناصر (معمولاً اعداد) هستند که همگی از یک نوع میباشند و با یک چندتایی، از اعداد صحیح مثبت اندیسگذاری میشوند. در NumPy ابعاد به نام محور (axe) شناخته میشوند. تعداد محورها رتبه (rank) نامیده میشود.
برای مثال، مختصات یک نقطه در فضای 3 بعدی [1, 2, 1] یک آرایه با رتبه 1 است زیرا یک محور دارد. این محور طولی بهاندازه 3 دارد. در مثال زیر آرایه رتبه 2 دارد (2 بعدی است). بعد (محور) نخست طولی به اندازه 2 دارد، بعد دوم طول 3 دارد.
[[ 1., 0., 0.], [ 0., 1., 2.]]
کلاس آرایه Numpy بهصورت ndarray نامگذاری شده است. همچنین بهصورت مستعار array نامیده میشود. توجه داشته باشید که numpy.array همان کلاس کتابخانه استاندارد پایتون به نام array.array نیست. کتابخانه استاندارد پایتون تنها آرایههای تکبعدی را مدیریت میکند و کاربردهای اندکی دارد. خصوصیات مهمتر یک ndarray بدین ترتیب هستند.
ndarray.ndim
تعداد محور (ابعاد) آرایه است. در دنیای پایتون تعداد ابعاد بهصورت رتبه نامیده میشود.
ndarray.shape
ابعاد یک آرایه است. این خصوصیت از یک چندتایی اعداد صحیح تشکیل یافته است که نشاندهنده اندازه هر بعد آرایه هستند. برای یک ماتریس با n ردیف و m ستون، شکل (shape) بهصورت (n,m) خواهد بود. بدین ترتیب طول چندتایی shape برابر با رتبه آرایه یا تعداد ابعاد ndim است.
ndarray.size
تعداد کل عناصر آرایه است. این مقدار برابر با حاصلضرب اجزای shape است.
ndarray.dtype
نوع عناصر یک آرایه را توصیف میکند. فرد میتواند dtype آرایه را با استفاده از انواع استاندارد پایتون ایجاد یا توصیف کند. بهعلاوه NumPy انواع مخصوص به خود را نیز دارد. برای مثال numpy.int32، numpy.int16 و numpy.float64 نمونههایی از انواع آرایه تعریف شده در NumPy هستند.
ndarray.itemsize
اندازه بایتهای هر یک از عناصر آرایه است. برای نمونه itemsize یک آرایه از عناصری با نوع float64 برابر با 8 (64/8) است در حالی که itemsize یک آرایه از نوع complex32 برابر با 4 (32/8) است. این مقدار معادل ndarray.dtype.itemsize است.
ndarray.data
این بافر (buffer) حاوی عناصر واقعی آرایه است. بهطورمعمول ما نیاز نداریم از این خصوصیت استفاده کنیم، زیرا با استفاده از امکان اندیسگذاری میتوانیم به عناصر آرایه دسترسی داشته باشیم.
مثال
>>> from numpy import * >>> a = arange(15).reshape(3, 5) >>> a array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14]]) >>> a.shape (3, 5) >>> a.ndim 2 >>> a.dtype.name 'int32' >>> a.itemsize 4 >>> a.size 15 >>> type(a) numpy.ndarray >>> b = array([6, 7, 8]) >>> b array([6, 7, 8]) >>> type(b) numpy.ndarray

ایجاد آرایه
چند روش برای ایجاد آرایه وجود دارند. برای مثال، میتوان با استفاده از تابع array یک آرایه را از فهرست معمولی پایتون یا چندتاییها ایجاد کرد. نوع آرایه حاصل، برابر با نوع عناصر موجود در دنبالههای تشکیل دهنده آن خواهد بود.
>>> from numpy import *
>>> a = array( [2,3,4] )
>>> a
array([2, 3, 4])
>>> a.dtype
dtype('int32')
>>> b = array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64')
یکی از خطاهای رایج در کار کردن با آرایههای چندبعدی زمانی رخ میدهد که قصد داریم array را با چند آرگومان عددی فراخوانی کنیم، در حالی که باید از فهرست منفردی از اعداد به عنوان آرگومان استفاده کنیم.
>>> a = array(1,2,3,4) # اشتباه >>> a = array([1,2,3,4]) # صحیح
array دنبالهای از دنبالهها را به آرایههای چندبعدی تبدیل میکند، دنبالهای از دنبالههای دنبالهها به آرایههای سهبعدی تبدیل میشود و همینطور تا آخر.
>>> b = array( [ (1.5,2,3), (4,5,6) ] ) >>> b array([[ 1.5, 2. , 3. ], [ 4. , 5. , 6. ]])
نوع آرایه را میتوان در زمان ایجاد آن به طور صریح تعیین کرد.
>>> c = array( [ [1,2], [3,4] ], dtype=complex ) >>> c array([[ 1.+0.j, 2.+0.j], [ 3.+0.j, 4.+0.j]])
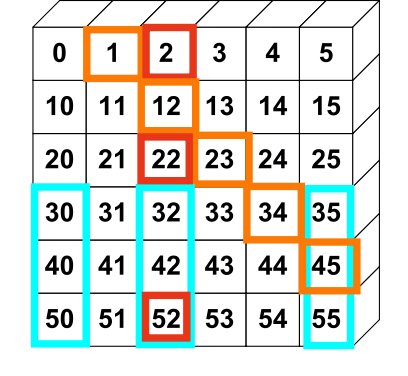
معمولاً عناصر یک آرایه از ابتدا مشخص نیستند، اما اندازه آن مشخص است. از اینرو NumPy چند تابع برای ایجاد آرایه با جایگاههای ابتدایی مشخص پیشنهاد میکند. بدین ترتیب در ادامه نیازی به بسط آرایه که عملیات پرهزینهای است، وجود نخواهد داشت. تابع zeros یک آرایه با مقادیر تماماً صفر ایجاد میکند. تابع ones یک آرایه با مقادیر 1 تولید میکند و تابع empty یک آرایه ایجاد میکند که محتوای اولیه آن تصادفی است و به وضعیت حافظه بستگی دارد. به طور پیشفرض dtype آرایه ایجاد شده، برابر با float64 است.
>>> zeros( (3,4) ) array([[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]) >>> ones( (2,3,4), dtype=int16 ) # را هم میتوان تعیین کرد dtype array([[[ 1, 1, 1, 1], [ 1, 1, 1, 1], [ 1, 1, 1, 1]], [[ 1, 1, 1, 1], [ 1, 1, 1, 1], [ 1, 1, 1, 1]]], dtype=int16) >>> empty( (2,3) ) array([[ 3.73603959e-262, 6.02658058e-154, 6.55490914e-260], [ 5.30498948e-313, 3.14673309e-307, 1.00000000e+000]])
NumPy برای ایجاد دنبالههایی از اعداد یک تابع مشابه range ارائه کرده است که بهجای لیست، یک آرایه برمیگرداند.
>>> arange( 10, 30, 5 ) array([10, 15, 20, 25]) >>> arange( 0, 2, 0.3 ) # آرگومانهای اعشاری میپذیرد array([ 0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8]
زمانی که arange با آرگومانهای اعشاری استفاده میشود، به دلیل دقت متناهی اعداد اعشاری، عموماً امکان پیشبینی تعداد عناصر به دست آمده وجود ندارد. به همین دلیل معمولاً استفاده از تابع linspace که تعداد عناصر مطلوب را نیز به عنوان یک آرگومان میگیرد، بهتر است:
1>>> linspace( 0, 2, 9 ) # 9 عدد از 0 تا 2
2array([ 0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])
3>>> x = linspace( 0, 2*pi, 100 ) # برای تابع ارزیابی در نقاط زیاد مناسب است
4>>> f = sin(x)پرینت کردن آرایهها
زمانی که یک آرایه را پرینت میکنید NumPy آن را به صوت یک فهرست تودرتو نمایش میدهد که طرح کلی آن بهصورت زیر است:
- آخرین محور از چپ به راست پرینت میشود.
- محور ماقبل آخر از بالا به پایین پرینت میشود.
- باقی محورها نیز از بالا به پایین پرینت و هرکدام با یک خط خالی از قبلی جدا میشوند.
بدین ترتیب آرایههای تکبعدی بهصورت ردیفی، آرایههای دوبعدی بهصورت ماتریس و آرایههای سهبعدی بهصورت فهرستی از ماتریسها پرینت میشوند.
1>>> a = arange(6) # 1d آرایه
2>>> print a
3[0 1 2 3 4 5]
4>>>
5>>> b = arange(12).reshape(4,3) # 2d آرایه
6>>> print b
7[[ 0 1 2]
8[ 3 4 5]
9[ 6 7 8]
10[ 9 10 11]]
11>>>
12>>> c = arange(24).reshape(2,3,4) # 3d آرایه
13>>> print c
14[[[ 0 1 2 3]
15[ 4 5 6 7]
16[ 8 9 10 11]]
17[[12 13 14 15]
18[16 17 18 19]
19[20 21 22 23]]]اگر یک آرایه برای پرینت گرفتن بسیار بزرگ باشد، NumPy به طور خودکار بخش مرکزی آرایه را قطع میکند و تنها ابتدا و انتهای آن را نمایش میدهد.
1>>> print arange(10000)
2[ 0 1 2 ..., 9997 9998 9999]
3>>>
4>>> print arange(10000).reshape(100,100)
5[[ 0 1 2 ..., 97 98 99]
6[ 100 101 102 ..., 197 198 199]
7[ 200 201 202 ..., 297 298 299]
8...,
9[9700 9701 9702 ..., 9797 9798 9799]
10[9800 9801 9802 ..., 9897 9898 9899]
11[9900 9901 9902 ..., 9997 9998 9999]برای اینکه این حالت را غیرفعال کنیم و NumPy کل آرایه را پرینت بگیرد، میتوانیم با استفاده از گزینه set_printoptions رفتار آن را تغییر دهیم.
1>>> set_printoptions(threshold='nan')عملیاتهای پایه
عملیاتهای حسابی بر روی آرایهها در سطح عناصر انجام مییابند. درنتیجه اجرای عملیات حسابی یک آرایه جدید ایجاد و مقادیر آن پر میشود.
1>>> a = array( [20,30,40,50] )
2>>> b = arange( 4 )
3>>> b
4array([0, 1, 2, 3])
5>>> c = a-b
6>>> c
7array([20, 29, 38, 47])
8>>> b**2
9array([0, 1, 4, 9])
10>>> 10*sin(a)
11array([ 9.12945251, -9.88031624, 7.4511316 , -2.62374854])
12>>> a<35
13array([True, True, False, False], dtype=bool)برخلاف بسیاری از زبانهای ماتریسی عملگر * در آرایههای NumPy بهصورت عنصر به عنصر، عمل ضرب را انجام میدهد. ضرب ماتریسی را میتوان با استفاده از تابع dot یا ایجاد اشیای matrix انجام داد.
1>>> A = array( [[1,1],
2... [0,1]] )
3>>> B = array( [[2,0],
4... [3,4]] )
5>>> A*B # ضرب در سطح عناصر
6array([[2, 0],
7[0, 4]])
8>>> dot(A,B) # ضرب در سطح ماتریس
9array([[5, 4],
10[3, 4]])برخی عملیاتها مانند += و *= بهجای ایجاد یک آرایه جدید بر روی همان ماتریس موجود عمل میکنند.
1>>> a = ones((2,3), dtype=int)
2>>> b = random.random((2,3))
3>>> a *= 3
4>>> a
5array([[3, 3, 3],
6[3, 3, 3]])
7>>> b += a
8>>> b
9array([[ 3.69092703, 3.8324276 , 3.0114541 ],
10[ 3.18679111, 3.3039349 , 3.37600289]])
11>>> a += b # به مقدار صحیح تبدیل میشود b
12>>> a
13array([[6, 6, 6],
14[6, 6, 6]])زمانی که بر روی آرایههایی با انواع مختلف، عملیاتی انجام میگیرد، نوع آرایه حاصل متناظر با نوع آرایه عمومیتر یا دقیقتر خواهد بود (این حالت به نام upcasting نامیده میشود).
1>>> a = ones(3, dtype=int32)
2>>> b = linspace(0,pi,3)
3>>> b.dtype.name
4'float64'
5>>> c = a+b
6>>> c
7array([ 1. , 2.57079633, 4.14159265])
8>>> c.dtype.name
9'float64'
10>>> d = exp(c*1j)
11>>> d
12array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j,
13-0.54030231-0.84147098j])
14>>> d.dtype.name
15'complex128'بسیاری از عملیاتهای تک آرایهای مانند جمع زدن همه عناصر یک آرایه بهصورت متدهایی در کلاس ndarray اجرا میشوند.
1>>> a = random.random((2,3))
2>>> a
3array([[ 0.6903007 , 0.39168346, 0.16524769],
4[ 0.48819875, 0.77188505, 0.94792155]])
5>>> a.sum()
63.4552372100521485
7>>> a.min()
80.16524768654743593
9>>> a.max()
100.9479215542670073این عملیاتها به طور پیشفرض طوری بر روی آرایهها اجرا میشوند که صرفنظر از شکلشان، گویی آرایهها فهرستی از اعداد هستند. بااینحال با تعیین پارامتر axis میتوان یک عملیات را در راستای یک محور تعیین شده در یک آرایه اجرا کرد:
1>>> b = arange(12).reshape(3,4)
2>>> b
3array([[ 0, 1, 2, 3],
4[ 4, 5, 6, 7],
5[ 8, 9, 10, 11]])
6>>>
7>>> b.sum(axis=0) # sum of each column
8array([12, 15, 18, 21])
9>>>
10>>> b.min(axis=1) # min of each row
11array([0, 4, 8])
12>>>
13>>> b.cumsum(axis=1) # cumulative sum along each row
14array([[ 0, 1, 3, 6],
15[ 4, 9, 15, 22],
16[ 8, 17, 27, 38]])تابعهای سراسری
NumPy تابعهای ریاضیاتی متداولی مانند sin، cos و exp را در خود دارد. در NumPy این توابع به نام «تابعهای سراسری» (ufanc) نامیده میشوند. درون NumPy این تابعها در سطح عناصر یک آرایه اجرا میشوند و درنتیجه یک آرایه جدید ایجاد میکنند.
1>>> B = arange(3)
2>>> B
3array([0, 1, 2])
4>>> exp(B)
5array([ 1. , 2.71828183, 7.3890561 ])
6>>> sqrt(B)
7array([ 0. , 1. , 1.41421356])
8>>> C = array([2., -1., 4.])
9>>> add(B, C)
10array([ 2., 0., 6.])اندیسگذاری، قطعهبندی و تکرار
آرایههای تکبعدی را میتوان همانند فهرستها و دیگر دنبالههای پایتون، اندیسگذاری کرد، قطعهبندی نمود و عملیاتی را بر روی آنها تکرار کرد.
1>>> a = arange(10)**3
2>>> a
3array([ 0, 1, 8, 27, 64, 125, 216, 343, 512, 729])
4>>> a[2]
58
6>>> a[2:5]
7array([ 8, 27, 64])
8>>> a[:6:2] = -1000 # equivalent to a[0:6:2] = -1000; from start to position 6, exclusive, set every 2nd element to -1000
9>>> a
10array([-1000, 1, -1000, 27, -1000, 125, 216, 343, 512, 729])
11>>> a[::-1] # reversed a
12array([ 729, 512, 343, 216, 125, -1000, 27, -1000, 1, -1000])
13>>> for i in a:
14... print i**(1/3.),
15...
16nan 1.0 nan 3.0 nan 5.0 6.0 7.0 8.0 9.0آرایههای چندبعدی میتوانند برای هر محور خود یک اندیس داشته باشند. این اندیسها در یک چندتایی که با کاما از هم جدا میشود ارائه میشوند:
1>>> def f(x,y):
2... return 10*x+y
3...
4>>> b = fromfunction(f,(5,4),dtype=int)
5>>> b
6array([[ 0, 1, 2, 3],
7[10, 11, 12, 13],
8[20, 21, 22, 23],
9[30, 31, 32, 33],
10[40, 41, 42, 43]])
11>>> b[2,3]
1223
13>>> b[0:5, 1] # bهر ردیف در ستون دوم
14array([ 1, 11, 21, 31, 41])
15>>> b[: ,1] # معادل مثال قبلی
16array([ 1, 11, 21, 31, 41])
17>>> b[1:3,: ] # b هر ستون در ردیف دوم و سوم
18array([[10, 11, 12, 13],
19[20, 21, 22, 23]])زمانی که تعداد اندیسها کمتر از تعداد محورها باشد، اندیسهای ناموجود بهصورت قطعههای کامل در نظر گرفته میشوند:
1>>> b[-1] # b[-1,:]ردیف آخر و معادل
2array([40, 41, 42, 43])در مورد آرایه [b[i عبارت داخل براکت را میتوان بدینصورت نوشت که ابتدا یک «i» قرار داد و سپس به تعداد محورهای باقیمانده «:» قرار داد. NumPy امکان استفاده از نقطه را نیز دارد یعنی [...,b[i.
نقطهها (...) بدین معنی است که به NumPy میگوییم هر مقدار دونقطه (:) دیگر که نیاز است بگذار تا یک چندتایی کامل برای اندیسها ایجاد شود.
1>>> c = array( [ [[ 0, 1, 2], # یک آرایه 3 بعدی (دو آرایه 2بعدی پشته شده)
2... [ 10, 12, 13]],
3...
4... [[100,101,102],
5... [110,112,113]] ] )
6>>> c.shape
7(2, 2, 3)
8>>> c[1,...] # c[1,:,:] یا c[1]همانند
9array([[100, 101, 102],
10[110, 112, 113]])
11>>> c[...,2] # c[:,:,2] همانند
12array([[ 2, 13],
13[102, 113]])تکرار عملیات بر روی آرایههای چندبعدی با توجه به محور نخست انجام مییابد.
1>>> for row in b:
2... print row
3...
4[0 1 2 3]
5[10 11 12 13]
6[20 21 22 23]
7[30 31 32 33]
8[40 41 42 43]بااینحال، اگر کسی بخواهد یک عملیات را بر روی همه عناصر یک آرایه اجرا کند، میتواند از خصوصیت flat استفاده کند که باعث میشود عملیات بر روی همه عناصر آرایه تکرار شود:
1>>> for element in b.flat:
2... print element,
3...
40 1 2 3 10 11 12 13 20 21 22 23 30 31 32 33 40 41 42 43
5
دستکاری شکل
چگونه میتوانیم شکل یک آرایه را تغییر دهیم؟ هر آرایهای شکلی دارد که بر اساس تعداد عناصر هر محور تعیین میشود:
1>>> a = floor(10*random.random((3,4)))
2>>> a
3array([[ 7., 5., 9., 3.],
4[ 7., 2., 7., 8.],
5[ 6., 8., 3., 2.]])
6>>> a.shape
7(3, 4)شکل یک آرایه را میتوان بهوسیله فرمانهای مختلف تغییر داد:
1>>> a.ravel() # مسطح سازی آرایه
2array([ 7., 5., 9., 3., 7., 2., 7., 8., 6., 8., 3., 2.])
3>>> a.shape = (6, 2)
4>>> a.transpose()
5array([[ 7., 9., 7., 7., 6., 3.],
6[ 5., 3., 2., 8., 8., 2.]])ترتیب عناصر در آرایه حاصل از ()ravel بهطورمعمول به «سبک C» هستند یعنی اندیس منتهیالیه سمت راست «سریعتر از بقیه تغییر مییابد» بنابراین عنصر بعد از [a[0,0، عنصر [a[0,1 است. اگر شکل آرایه تغییر یابد، در حالت جدید هم بهصورت «سبک C» با آن برخورد میشود. NumPy بهطورمعمول آرایههایی ایجاد میکند که به این ترتیب ذخیره میشوند. بنابراین برای کپی کردن آرگومانهای آن نیازی به ()ravel نیست، اما اگر آرایه با استفاده از تکههایی از آرایههای دیگر یا با استفاده از گزینههای نامعمول ایجاد شده باشد، ممکن است نیاز باشد که ()ravel نیز کپی شود. تابعهای ()ravel و ()reshape را نیز میتوان با استفاده از آرگومانهای اختیاری تغییر داد و مثلاً از آرایههایی به سبک فرترن (FORTRAN) استفاده کرد که در آنها اندیس منتهیالیه سمت چپ قبل از همه تغییر مییابد.
تابع reshape آرگومانش را با شکل تغییر یافتهای برمیگرداند، در حالی که تابع resize خود آرایه را تغییر میدهد:
1>>> a
2array([[ 7., 5.],
3[ 9., 3.],
4[ 7., 2.],
5[ 7., 8.],
6[ 6., 8.],
7[ 3., 2.]])
8>>> a.resize((2,6))
9>>> a
10array([[ 7., 5., 9., 3., 7., 2.],
11[ 7., 8., 6., 8., 3., 2.]])اگر یک بعد در طی عملیات reshape بهصورت 1- تعیین شده باشد در این صورت ابعاد دیگر به طور خودکار محاسبه میشوند:
1>>> a.reshape(3,-1)
2array([[ 7., 5., 9., 3.],
3[ 7., 2., 7., 8.],
4[ 6., 8., 3., 2.]])پشتهسازی (Stacking) با آرایههای مختلف
میتوان از چند آرایه برای پشتهسازی در راستای محورهای مختلف استفاده کرد:
1>>> a = floor(10*random.random((2,2)))
2>>> a
3array([[ 1., 1.],
4[ 5., 8.]])
5>>> b = floor(10*random.random((2,2)))
6>>> b
7array([[ 3., 3.],
8[ 6., 0.]])
9>>> vstack((a,b))
10array([[ 1., 1.],
11[ 5., 8.],
12[ 3., 3.],
13[ 6., 0.]])
14>>> hstack((a,b))
15array([[ 1., 1., 3., 3.],
16[ 5., 8., 6., 0.]])تابع column_stack آرایههای یکبعدی را بهصورت ستونهایی در یک آرایه دوبعدی پشته میکند. این تابع معادل تابع vstack است که تنها در مورد آرایههای یکبعدی عمل میکند:
1>>> column_stack((a,b)) # با آرایههای 2 بعدی
2array([[ 1., 1., 3., 3.],
3[ 5., 8., 6., 0.]])
4>>> a=array([4.,2.])
5>>> b=array([2.,8.])
6>>> a[:,newaxis] # بدین ترتیب میتوان برداری با ستونهای 2 بعدی داشت
7array([[ 4.],
8[ 2.]])
9>>> column_stack((a[:,newaxis],b[:,newaxis]))
10array([[ 4., 2.],
11[ 2., 8.]])
12>>> vstack((a[:,newaxis],b[:,newaxis])) # متفاوت است vstack رفتار
13array([[ 4.],
14[ 2.],
15[ 2.],
16[ 8.]])از سوی دیگر، تابع row_stack آرایههای یکبعدی را بهصورت ردیفهایی در آرایههای دوبعدی، پشته میکند. برای آرایههایی با ابعادی بیش از 2، تابع hstack در راستای محور دوم و vstack در راستای محور اول پشتهسازی میکند و تابع concatenate امکان تعیین تعداد محورهایی که پشتهسازی در راستای آنها انجام میگیرد را مهیا کرده است. در موارد پیچیدهتر تابعهای []_r و []_c برای ایجاد آرایههایی با پشتهسازی در راستای یک محور، مناسب هستند. این توابع امکان استفاده از عبارتهای محدودهای (":") را فراهم کردهاند:
1>>> r_[1:4,0,4]
2array([1, 2, 3, 0, 4])[]_r و []_ c وقتی بر روی آرایهها به عنوان آرگومان استفاده میشوند، مشابه توابع vstack و hstack با رفتار پیشفرض عمل میکنند، اما این مزیت اضافی را دارند که امکان تعریف کردن تعداد محورهایی که پشتهسازی در راستای آنها انجام میشود را دارند.
افراز کردن یک آرایه به چند آرایه کوچکتر
با استفاده از تابع hsplit میتوان یک آرایه را در راستای محورهای افقیاش افراز کرد. این کار یا با تعیین تعداد آرایههای همشکلی که باید بازگردانده شوند، انجام میگیرد یا با تعیین ستونهایی که پس از آنها باید عمل تقسیم کردن انجام گیرد.
1>>> a = floor(10*random.random((2,12)))
2>>> a
3array([[ 8., 8., 3., 9., 0., 4., 3., 0., 0., 6., 4., 4.],
4[ 0., 3., 2., 9., 6., 0., 4., 5., 7., 5., 1., 4.]])
5>>> hsplit(a,3) # به 3 بخش افراز میکند
6[array([[ 8., 8., 3., 9.],
7[ 0., 3., 2., 9.]]), array([[ 0., 4., 3., 0.],
8[ 6., 0., 4., 5.]]), array([[ 0., 6., 4., 4.],
9[ 7., 5., 1., 4.]])]
10>>> hsplit(a,(3,4)) # آن را پس از ستونهای سوم و چهارم افراز میکند
11[array([[ 8., 8., 3.],
12[ 0., 3., 2.]]), array([[ 9.],
13[ 9.]]), array([[ 0., 4., 3., 0., 0., 6., 4., 4.],
14[ 6., 0., 4., 5., 7., 5., 1., 4.]])]تابع Vsplit آرایه را در راستای محورهای عمودی افراز میکند و تابع array split امکان تعیین دقیق محورهایی که باید افراز شوند را فراهم کرده است.
کپیها و نمایشها
زمانی که بر روی آرایهها عملیاتی انجام میدهیم یا آنها را دستکاری میکنیم، در برخی موارد دادههای آنها به یک آرایه جدید کپی میشود و در برخی موارد نیز چنین نمیشود. این مسئله موجب سردرگمی افراد مبتدی میشود. بهطورکلی سه حالت وجود دارد:
هیچ کپی انجام نمیشود
در انتسابهای ساده هیچ کپی از اشیای آرایه یا دیگر دادهها ایجاد نمیشود.
1>>> a = arange(12)
2>>> b = a # هیچ شی جدیدی ایجاد نمیشود
3>>> b is a # هستند ndarray هر دو همان شی
4True
5>>> b.shape = 3,4 # شکل آن تغییر مییابد
6>>> a.shape
7(3, 4)پایتون اشیای تغییرپذیر را بهصورت مرجع ارسال میکند بنابراین فراخوانهای تابع هیچ کپی جدیدی ایجاد نمیکنند.
1>>> def f(x):
2... print id(x)
3...
4>>> id(a) # شناساگر منحصربهفرد شیء استid
5148293216
6>>> f(a)
7148293216
نمایش (view) یا کپی سطحی
اشیای آرایهای مختلف میتوانند دادههای مشترکی داشته باشند. متد view یک شی آرایهای جدید ایجاد میکند که از دادههای مشابهی استفاده میکند.
1>>> c = a.view()
2>>> c is a
3False
4>>> c.base is a # استa نمایشی از دادههایی است که متعلق به c
5True
6>>> c.flags.owndata
7False
8>>>
9>>> c.shape = 2,6 # تغییر نمیکند a شکل
10>>> a.shape
11(3, 4)
12>>> c[0,4] = 1234 # تغییر میکند a دادههای
13>>> a
14array([[ 0, 1, 2, 3],
15[1234, 5, 6, 7],
16[ 8, 9, 10, 11]])قطعهبندی کردن یک آرایه یک نمایش (view) از آن بازمیگرداند:
1>>> s = a[: , 1:3] # "s = a[:,1:3]"برای خوانایی بیشتر فاصله اضافه شده است. همچنین میتوان نوشت:
2>>> s[:] = 10 # s[:] is a view of s. Note the difference between s=10 and s[:]=10
3>>> a
4array([[ 0, 10, 10, 3],
5[1234, 10, 10, 7],
6[ 8, 10, 10, 11]])کپی عمیق
متد copy یک کپی کامل از آرایه و دادههای آن ایجاد میکند.
1>>> d = a.copy() # یک شیء دادهای جدید با دادههای جدید ایجاد شده است
2>>> d is a
3False
4>>> d.base is a # هیچ چیز مشترکی ندارند. d و a
5False
6>>> d[0,0] = 9999
7>>> a
8array([[ 0, 10, 10, 3],
9[1234, 10, 10, 7],
10[ 8, 10, 10, 11]])در بخش دوم این مقاله، به بررسی مفاهیم و توابع پیشرفتهتری خواهیم پرداخت.
اگر تمایل به مطالعه بیشتر در مورد این موضوعات را داشته باشید؛ شاید آموزش های زیر نیز برای شما مفید باشند:
- آموزش برنامه نویسی پایتون
- آموزش ساخت ربات تلگرام با پایتون (Python)
- آموزش پایتون گرافیکی (رابط های گرافیکی پایتون)
- آموزش یادگیری ماشین (Machine Learning) با پایتون (Python)
#













با سلام و خسته نباشید
امکان این قسمت از مقاله رو یه توضیح مختصر بدین که چجوری این اتفاق میوفته؟
** در مثال زیر آرایه رتبه 2 دارد (2 بعدی است). بعد (محور) نخست طولی به اندازه 2 دارد، بعد دوم طول 3 دارد.
[[ 1., 0., 0.],
[ 0., 1., 2.]]