پایستگی و کوانتیده بودن بار الکتریکی | به زبان ساده

در این مطلب با مفهوم پایستگی و کوانتیده بودن بار الکتریکی آشنا می‌شویم. مهم است بدانید که منظور از کوانتیده چیزی است که به صورت تک تک قابل شمارش باشد؛ برای مثال دانه‌های برنج را می‌توان کمیتی کوانتیده معرفی کرد، ولی ماسه‌های ساحل به سختی به صورت تک تک قابل شمارش هستند. در این مطلب در مورد این ویژگی‌های بار الکتریکی صحبت خواهیم کرد.

پایستگی و کوانتیده بودن بار الکتریکی

پایستگی و کوانتیده بودن بار الکتریکی دو ویژگی مهم بارهای الکتریکی هستند. این واقعیت که همه بارهای مشاهده شده تاکنون همیشه مضرب صحیحی از ذره بنیادی $$e=1.6\times 10^{-19}\ C$$ هستند به عنوان کوانتیدگی بار الکتریکی شناخته می‌شود. بنابراین می‌توان نوشت بار الکتریکی برابر است با

$$q=\pm ne$$

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

که $$n=1,2,3,...$$ و $$e$$ اندازه کمترین بار الکتریکی است که می‌تواند توسط پروتون یا الکترون حمل شود. علت کوانتیدگی بار الکتریکی به این دلیل است که وقتی جسمی به جسم دیگر مالش داده می‌شود تعدادی الکترون بین دو جسم منتقل می‌شود. هیچ توضیحی علمی برای کوانتیدگی بار الکتریکی در تئوری‌های الکترودینامیک و فیزیک مدرن وجود ندارد اما می‌توان آن را به صورت تجربی تأیید کرد.

برای توضیح پایستگی و کوانتیده بودن بار الکتریکی در سطح میکروسکوپی Gell-Mann و Zweig فرض کردند که تمام ذرات بنیادی از اجزای تشکیل دهنده اولیه کوچکتری به نام کوارک ساخته شده‌اند. پروتون‌ها و نوترون‌ها از دو نوع کوارک (۱) کوارک‌های بالا که با u نمایش داده می‌شود و بار آن $$+\frac{2e}{3}$$ و (۲) کوارک‌های پایین که با d نمایش داده می‌شود و بار آن $$-\frac{e}{3}$$ است ساخته شده‌اند. بر اساس ساختار کوارکی، پروتون دارای ساختار $$uud$$ است و بار آن برابر با $$\frac{2e}{3}+\frac{2e}{3}-\frac{e}{3}=e$$ است. بر همین اساس ساختار یک نوترون $$udd$$ است و بار الکتریکی آن برابر با $$\frac{2e}{3}-\frac{e}{3}-\frac{e}{3}=0$$ است.

تا به امروز وجود کوارک از طریق آزمایشگاهی به طور مستقیم تایید نشده است اما از روش‌های غیر مستقیم وجود کوارک‌ها مورد تایید قرار گرفته است. در آینده زمانی که کوارک‌ها به صورت مستقیم مشاهده شوند تنها تغییری که در مفهوم کوانتیدگی بار به وجود می‌آید این است که کمیت کوانتیدگی از $$e$$ به $$\frac{e}{3}$$ تغییر می‌کند ولی نظریه کوانتیدگی بار به همین صورت باقی خواهد ماند.

همان طور که می‌دانید واحد بار الکتریکی کولن است، اما این واحد خیلی کاربردی نیست و در حقیقت یک واحد بزرگ است. فرض کنید جسمی را در نظر بگیریم که در هر ثانیه $$10^{9}$$ الکترون می‌دهد. زمان لازم برای داشتن بار الکتریکی برابر با ۱ کولن در این جسم را به روش زیر می‌توانیم محاسبه کنیم و داریم:

$$q=ne$$

$$n=\frac{q}{e}=\frac{1}{1.6\times 10^{-19}}=6.25\times 10^{18}$$

بدین ترتیب زمان لازم برای به دست آمدن بار الکتریکی ۱ کولنی برابر است با:

$$t=\frac{6.25\times 10^{18}}{10^{9}}=6.25\times 10^{9}\ seconds$$
$$\frac{6.25\times 10^{9}}{365\times 24\times 60\times 60}=198.2\ years$$

یعنی زمان لازم برای به دست آمدن یک بار ا کولنی چیزی بیش از ۱۹۸ سال است و این موضوع نشان می‌دهد که واحد کولن یک واحد بسیار بزرگ است و برای استفاده ما مفید نیست. بنابراین واحدهای کاربردی دیگری مانند میلی‌کولن، میکروکولن و نانوکولن استفاده می‌شود.

اصول پایستگی بار الکتریکی

بار الکتریکی نه ایجاد می‌شود و نه از بین می‌رود بلکه از یک سیستم به سیستم دیگر منتقل می‌شود، در نتیجه به طوری کلی بار یک سیستم منزوی ثابت می‌ماند.

بیان اول

هنگامی که یک میله شیشه‌ای (خنثی از نظر الکتریکی) با یک پارچه ابریشم مالش داده می‌شود (از نظر الکتریکی خنثی است)، الکترون‌های آزاد میله شیشه‌ای که نیروی اتصال ضعیف‌تری دارند به پارچه ابریشمی منتقل می‌شوند. بنابراین میله شیشه‌ای دچار کمبود الکترون شده و بار مثبت به دست می‌آورد در حالی که پارچه ابریشم بار منفی بیشتری دارد و بار کل آن منفی می‌شود. کل بار سیستم یعنی میله شیشه‌ای و پارچه ابریشم صفر می‌ماند.

بیان دوم

وقتی یک فوتون پرتوی $$\gamma$$ با انرژی برابر یا بیشتر از $$1.01$$ مگاالکترون‌ولت از نزدیکی هسته عبور می‌کند میدان الکتریکی ایجاد شده توسط هسته باعث از بین رفتن پرتوهای $$\gamma$$ و ایجاد یک جفت الکترون و پوزیترون می‌شود. این پدیده به تولید جفت معروف است و به صورت زیر نمایش داده می‌شود:

$$\gamma\rightarrow e^{-}+e^{+}$$

می‌توان دید که بار کل دو طرف تساوی صفر است.

بیان سوم

زمانی که یک الکترون و یک پوزیترون خیلی به یکدیگر نزدیک می‌شوند، از بین می‌روند و تولید دو پرتو گاما می‌کنند که انرژی هر یک $$0.51$$ مگاالکترون‌ولت است. این پدیده را نابودی ماده می‌نامند و به صورت زیر نمایش داده می‌شود:

$$e^{-}+e^{+}\rightarrow \gamma+\gamma$$

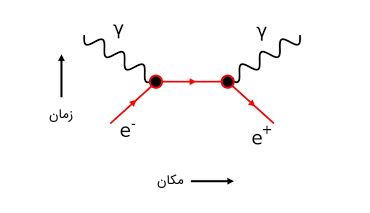
باز هم می‌توان مشاهده کرد که بار‌ الکتریکی هر دو طرف صفر است که بدین معنی است که پایستگی و کوانتیده بودن بار الکتریکی برقرار است.

بیان چهارم

واکنش زیر را در نظر بگیرید:

$$_{92}U^{238}\rightarrow_{90}U^{234}+_{2}He^{4}$$

می‌توان دید که بار هر دو طرف برابر با $$+92e$$ است.

بیان پنجم

واکنش هسته ای زیر را در نظر بگیرید:

$$_{92}U^{235}+ _{0}n^{1}\rightarrow_{56}Ba^{141}+_{36}Kr^{92}+3_{0}n^{1}+Energy$$

می‌توان دید که بار الکتریکی دو طرف واکنش برابر با $$+92e$$ است.

بارهای الکتریکی قابل جمع کردن هستند به این معنی که بار الکتریکی یک جسم برابر با مجموع بارهای الکتریکی است که در هر نقطه‌ای در جسم وجود دارند. وقتی عملیات جمع را انجام می‌دهیم باید به علامت بار الکتریکی دقت داشته باشیم و آن‌ها را در عملیات جمع وارد کنیم و در نهایت مثبت یا منفی بودن بار الکتریکی جسم باید بیان شود. در ادامه برای درک بهتر پایستگی و کوانتیده بودن بار الکتریکی به حل چند مثال می‌پردازیم.

مثال‌های پایستگی و کوانتیده بودن بار الکتریکی

مثال 1: چه مقدار بار الکتریکی لازم است تا به بار الکتریکی 1 کولن دست پیدا کنیم.

پاسخ: بار کل برابر با 1 کولن است، بار الکتریکی هر الکترون نیز برابر با $$e=1.6\times 10^{-19}\ C$$ است. تعداد بارهای الکتریکی به این معنی است که در رابطه $$q=ne$$ تعداد بارهای الکتریکی یعنی n را به دست آوریم. بدین ترتیب داریم:

$$q=ne\rightarrow 1=n\times 1.6\times 10^{-19}$$
$$\Rightarrow n=\frac{1}{1.6\times 10^{-19}}=6.25\times 10^{18}$$

مثال 2: چه تعدادی بار الکتریکی باید از یک جسم رسانا خارج کنیم تا در نهایت بار الکتریکی جسم برابر با $$q=3.5\ \mu C$$ شود.

پاسخ: بار الکتریکی $$q=3.5\ \mu C$$ بر حسب کولن برابر با $$q=3.5\ \mu C=3.5\times 10^{-6}\ C$$ است. با دانستن بار الکتریکی الکترون و استفاده از رابطه $$q=ne$$، می‌توانیم تعداد بارهای الکتریکی یا $$n$$ را به دست آوریم و داریم:

$$n=\frac{q}{e}=\frac{3.5\times 10^{-6}}{1.6\times 10^{-19}}=2.1875 \times10^{13}$$

بنابراین تعداد الکترون‌هایی که لازم است تا از جسم بگیریم تا بار الکتریکی آن برابر با $$q=3.5\ \mu C$$ شود برابر با $$2.1875 \times10^{13}$$ است.

مثال 3: تعداد بارهای مثبت و منفی 250 گرم آب در یک فنجان را به دست آوردید.

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

پاسخ: فرمول شیمیایی آب $$H_{2}O$$ است و جرم مولکولی آن برابر با $$18\ g\ mol^{-1}$$ است. تعداد مول‌های موجود در 250 گرم آب به صورت زیر قابل محاسبه است:

$$Nom.\ of\ moles=\frac{Given\ mass}{molecular\ mass}=\frac{250}{18}=13.89$$

هر مول ماده طبق ثابت آووگادرو شامل $$6.022 \times 10^{23}$$ مولکول است. پس $$13.89$$ مول از ماده شامل $$13.89\times6.022 \times 10^{23}$$ مولکول است و تعداد کل مولکول‌ها برابر با $$83.66\times 10^{23}$$ است.

تعداد الکترون‌‌های موجود در هر مولکول آب برابر 10 الکترون است. زیرا مولکول آب شامل 2 هیدروژن و یک اکسیژن است، هر هیدروژن 1 الکترون و هر اکسیژن 8 الکترون دارد ($$1\times 2 +8\times 1=10$$). در نتیجه تعداد کل الکترون‌های موجود در فنجان 250 گرمی از آب برابر است با:

$$83.66\times 10^{23}\times 10=83.66\times 10^{24}$$

بدین ترتیب بار الکتریکی منفی در فنجان برابر است با:

$$83.66\times 10^{24}\times 1.6 \times 10^{-19}=1.34 \times 10^{7}\ C$$

و چون آب از لحاظ الکتریکی خنثی است یعنی بار منفی و مثبت فنجان آب با هم برابر هستند، بدین ترتیب بار مثبت کل برابر با $$1.34 \times 10^{7}\ C$$ است.

مثال 4: تعداد الکترون‌های موجود در یک چراغ الکتریکی 100 واتی در ولتاژ 230 ولت در ثانیه چه قدر است؟

پاسخ: توان لامپ الکتریکی 100 وات و ولتاژ آن 230 ولت است. از رابطه توان الکتریکی می‌دانیم $$P=VI$$ و جریان الکتریکی برابر با $$I=\frac{q}{t}$$ است. با استفاده از این دو رابطه داریم:

$$q=\frac{P\ t}{V}=\frac{100\times 1}{230}=0.4348\ C$$

و با استفاده از رابطه $$q=ne$$ می‌توانیم تعداد بارهای الکتریکی را به دست آوریم. بدین ترتیب $$n$$ برابر است با:

$$\Rightarrow n=\frac{q}{e}=\frac{0.4348}{1.6 \times 10^{-19}}= 2.72 \times 10^{18}$$

پس تعداد الکترون‌هایی که در یک ثانیه از یک لامپ الکتریکی با توان 100 وات و در ولتاژ 230 ولت عبور می‌کنند برابر با $$2.72\times 10^{18}$$ الکترون است.

مثال 5: دو کره همسان یکی با بار الکتریکی $$q_{1}=-2 \mu C$$ و دیگری با بار الکتریکی $$q_{2}=14 \mu C$$ به گونه‌ای طراحی شده‌اند که با یکدیگر برخورد کرده و سپس از هم جدا شوند. بار الکتریکی هر کره بعد از جدا کردن کره‌ها چه قدر است؟

پاسخ: بار کل دو کره برابر با $$-2+14=+12$$ است. چون دو کره یکسان هستند بار الکتریکی به طور یکسان در آن‌ها تقسیم می‌شود. بدین ترتیب بعد از جدا کردن کره‌ها بار الکتریکی هر کره برابر با $$\frac{12}{2}=6\ \mu C$$ است.

جمع‌بندی

در این مطلب مباحث مربوط به پایستگی و کوانتیده بودن بار الکتریکی و اصول پایستگی بار الکتریکی را مورد بحث قرار دادیم، همچنین نشان دادیم که با پنج بیان مختلف می‌توان اصل پایستگی بار الکتریکی را توضیح داد. در نهایت این مطلب را با حل چند مثال به پایان رساندیم.