میدان مغناطیسی گردان — به زبان ساده
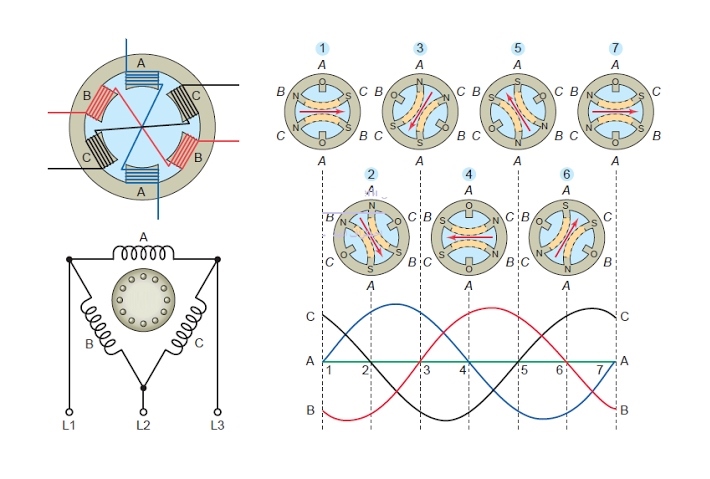
وقتی یک منبع سه فاز را به یک سیمپیچی سه فاز توزیع شده یک ماشین چرخان اعمال کنیم، یک میدان مغناطیسی گردان تولید میشود که با سرعت سنکرون میچرخد. در این آموزش، درباره میدان مغناطیسی گردان بحث خواهیم کرد.
برای درک بهتر مفهوم میدان گردان، یک موتور الکتریکی سه فاز را در نظر میگیریم و برآیند شار سه فاز آن را در لحظات مختلف به دست میآوریم. خواهیم دید که نتیجه جمع برداری شار سه فاز یک شار چرخان خواهد بود.
ابتدا استاتور یک موتور الکتریکی را در نظر بگیرید که سیمپیچی هر سه فاز آن از نظر فیزیکی روی هسته استاتور توزیع شده و به اندازه $$120 ^ \circ $$ با هم فاصله دارند.
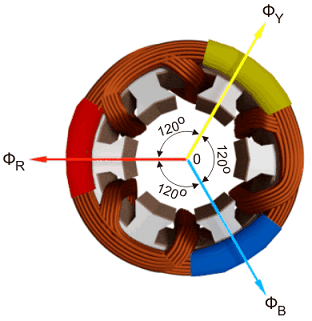
اگرچه جمع برداری سه جریان در یک سیستم سه فاز متعادل صفر است، حاصل میدانهای مغناطیسی تولیدی ناشی این جریانها صفر نیست و مقدار ثابتی دارد که نسبت به زمان در فضا میچرخد.
شار مغناطیسی تولیدی جریان هر فاز را میتوان با معادلات زیر نمایش داد. این معادلات شبیه نمایش جریان سیستم سه فاز است که شار نسبت به ولتاژ عمود است.
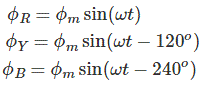
که در آن، $$ \phi _R$$، $$ \phi _Y$$ و $$ \phi _B$$ شارهای لحظهای متناظر با سیمپیچیهای قرمز، زرد و آبی هستند و $$ \phi _m $$ دامنه شار است. شکل موج شارها در فضا را میتوان با شکل زیر نمایش داد:
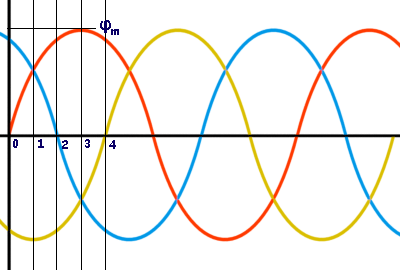
نقطه $$0$$ شکل بالا را در نظر بگیرید. مقدار $$ \phi _R $$ در این نقطه برابر است با:
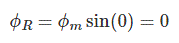
برای مقدار $$ \phi _Y$$ نیز داریم:
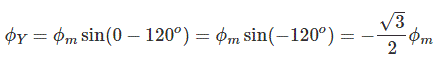
و مقدار $$ \phi _ B $$ برابر است با:
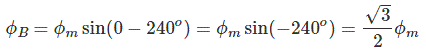
مجموع این شارها در این لحظه، برابر با $$ \phi _r = 1.5 \phi _ m $$ است و در شکل زیر نشان داده شده است.
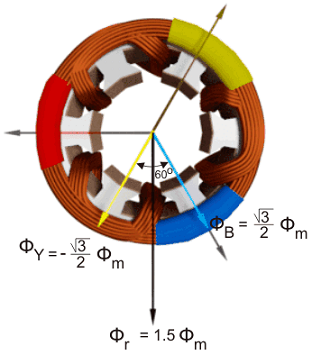
اکنون در نمودار شکل موجها، نقطه $$1$$ را در نظر بگیرید که متناظر با $$ \omega t = \pi / 6 $$ یا $$ 30 ^ \circ $$ است.
در نتیجه، مقدار $$ \phi _ r$$ در این نقطه برابر است با:
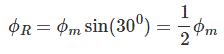
همچنین برای $$ \phi _ Y $$ داریم:
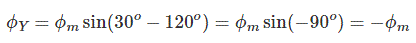
مقدار $$ \phi _ B $$ نیز برابر است با:
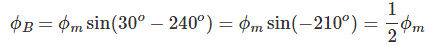
نتیجه این شارها در نقطه مورد نظر، برابر با $$ \phi _r = 1.5 \phi _ m $$ بوده و در شکل زیر نشان داده شده است.
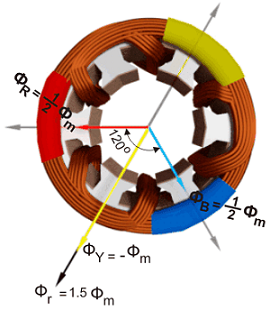
حال نقطه $$2$$ را در نظر بگیرید که در آن، $$ \omega t = \pi / 3 $$ یا $$ 60 ^ \circ $$ است.
در این نقطه، مقدار $$ \phi _R$$ برابر است با:
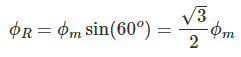
مقادیر $$ \phi _Y$$ و $$ \phi _ Y $$ نیز به صورت زیر هستند:
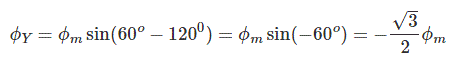
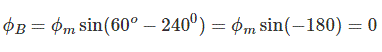
مجموع این شارها در نقطه مذکور برابر با $$ \phi _ r = 1.5 \phi _m $$ است که در شکل زیر نشان داده شده است. واضح است که بردار شار حاصل، به اندازه $$ 30 ^ \circ $$ در جهت عقربههای ساعت و بدون تغییر اندازه چرخیده است.
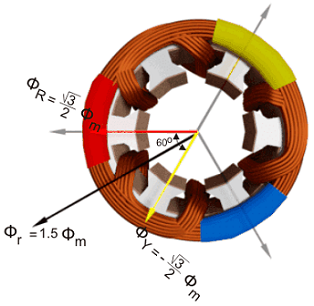
اکنون نقطه $$3$$ را در نظر بگیرید که در آن، $$ \omega t = \pi / 2 $$ یا $$ 90 ^ \circ $$ است.
در این نقطه، مقدار $$ \phi _R$$، $$ \phi _ Y $$ و $$ \phi _ B$$ به صورت زیر هستند:
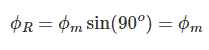
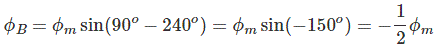
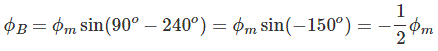
نتیجه این شارها نیز برابر با $$ \phi _r = 1.5 \phi _m$$ است که در شکل زیر نشان داده شده است. 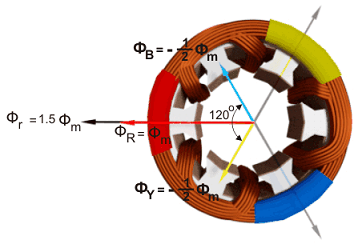
همانطور که میبینیم، بردار شار حاصل به اندازه $$ 30 ^ \circ $$ در جهت عقربههای ساعت چرخیده است.
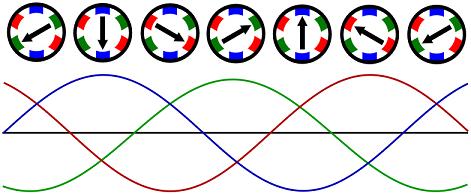
شکل زیر میدان مغناطیسی سه فاز چرخان را برای لحظات مختلف نشان میدهد (بردارهای سیاه).
اگر به یادگیری مباحث مشابه این مطلب علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- اصول عملکرد ترانسفورماتور — به زبان ساده
- مدارهای مغناطیسی — به زبان ساده
- کنترل موتورهای الکتریکی — به زبان ساده
^^











سلام . با سپاس از مجله فرادرس ، درخواستی داشتم مبنی بر این که ، درباره نحوه چرخش میدان مغناطیسی دوّار استاتور سه فاز چهارقطب توضیحی بدین . یک روز کامل توی اینترنت وقت گذاشتم ولی مطلبی پیدا نکردم . اگه توضیح همراه انیمیشن باشه که خیلی خوش فهم تر میشه .