معیار پایداری راث هرویتز — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در آموزش‌های پیشین مجله فرادرس، مباحث مربوط به نمایش سیستم‌های کنترل را بیان کردیم. تحلیل و طراحی سیستم‌های کنترل، مبتنی بر سه ویژگی مهم پاسخ گذرا، پایداری و خطای حالت ماندگار است. در این آموزش، یکی از ابزارهای بررسی پایداری سیستم‌های خطی، یعنی معیار پایداری راث هرویتز را معرفی خواهیم کرد.

معیار پایداری راث هرویتز، الگوریتم ساده‌ای است که با استفاده از آن می‌توان تعیین کرد که همه صفرهای یک چندجمله‌ای در سمت چپ صفحه مختلط قرار دارند (گاهی چنین چندجمله‌ای را هرویتز می‌نامند) یا خیر. چندجمله‌ای هرویتز،‌ یک التزام اساسی برای پایدار بودن (خروجی کران‌دار به‌ ازای ورودی کران‌دار) یک سیستم تغییرناپذیر با زمان پیوسته خطی (LTI) است.

شرط لازم پایداری

شرط لازم پایداری یک سیستم LTI، «هرویتز» (Hurwitz) بودن چندجمله‌ای است. یعنی همه صفرهای چندجمله‌ای در سمت چپ صفحه مختلط قرار داشته باشند. اگر حتی یکی از ریشه‌ها در سمت راست صفحه مختلط باشند، چندجمله‌ای پایدار نیست.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

شرط کافی پایداری

شرایط کافی پایداری، شرایطی است که اگر برقرار باشد، چندجمله‌ای پایدار خواهد بود. برای مثال، همان‌طور که خواهیم دید، شرط لازم و کافی یک سیستم LTI با معیار پایداری راث هرویتز، این است که همه درایه‌های ستوان اول آرایه راث هم‌علامت باشند.

معیار راث هرویتز

معیار راث هرویتز (Routh-Hurwitz Criterion)، هر دو شرط لازم و کافی را برای هرویتز بودن یک چندجمله‌ای بیان می‌کند و شامل سه آزمون مجزا است که باید هر سه آن‌ها برقرار باشد. اگر هر کدام از این آزمون‌ها برقرار نباشد، سیستم پایدار نیست و نیازی به انجام آزمون‌های دیگر نیست. به همین دلیل، آزمون‌ها را از آسان‌ترین به سخت‌ترین انجام می‌دهیم.

فیلم آموزش کاربرد متلب در کنترل خطی در فرادرس

کلیک کنید

آزمون راث هرویتز برای مخرج تابع تبدیل سیستم، یعنی معادله مشخصه انجام می‌شود؛ برای مثال، در یک تابع تبدیل حلقه‌ بسته با $$G(S)$$ در مسیر پیشِ‌رو و حلقه فیدبک $$H(s)$$، داریم:

$$\large T ( s ) = \frac { G ( s ) } { 1 + G ( s ) H ( s ) }$$

اگر این تابع تبدیل را ساده کنیم، یک کسر با صورت $$N(s)$$ و مخرج $$D(s)$$ خواهیم داشت:

$$\large T ( s ) = \frac { N ( s ) } { D ( s ) }$$

معیار پایداری راث هرویتز بر چندجمله‌ای مخرج $$D(s)$$ اعمال می‌شود.

آزمون‌های راث هرویتز

در اینجا، سه آزمون یا قاعده معیار راث هرویتز را بیان می‌کنیم. برای سادگی، فرض می‌کنیم درجه چندجمله‌ای (بزرگترین توان $$s$$ در $$D(s)$$) $$N$$ باشد. معادله $$D(s)$$ را می‌توان به‌ فرم عمومی زیر نوشت:

$$\large D ( s ) = a _ 0 + a _ 1 s + a _ 2 s ^ 2 + \cdots + a _ N s ^ N$$

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

قاعده ۱: همه ضرایب $$a_i$$ باید غیرصفر باشند.

قاعده ۲: همه ضرایب $$a_i$$ باید مثبت باشند (یا همه آن‌ها منفی باشند).

قاعده ۳: اگر قاعده ۱ و قاعده ۲، هر دو برقرار باشند، آن‌گاه آرایه راث را برای ضرایب $$a_i$$ تشکیل می‌دهیم. به‌ ازای هر یک تغییر علامت در درایه‌های ستون اول آرایه راث، یک قطب در سمت راست صفحه $$s$$ وجود دارد (اگر تغییر علامت داشته باشیم، سیستم ناپایدار خواهد بود).

آرایه راث به‌صورت زیر تشکیل می‌شود.

آرایه راث

آرایه راث با قرار دادن ضرایب $$a_i$$ چندجمله‌ای $$D(s)$$ در کنار هم (و مطابق چینش زیر) تشکیل می‌شود. ستون آخر این آرایه را برابر صفر قرار می‌دهیم.

$$\large \begin {matrix} s ^ N \\ s ^ { N - 1 } \end {matrix} \begin {vmatrix} a _ N & a _ { N - 2 } & \cdots & 0 \\ a _ { N - 1 } & a _ { N - 3 } & \cdots & 0 \end {vmatrix}$$

از آرایه بالا مشخص است که اگر $$N$$ فرد باشد، سطر اول فقط شامل ضرایب توان‌های جملات فرد چندجمله‌ای است و اگر $$N$$ زوج باشد، ضرایب زوج، سطر اول را تشکیل می‌دهند.

از سطرهای بعدی (از سوم و بعد از آن) آرایه راث را به‌ صورت زیر تکمیل می‌کنیم:

$$\large \begin {matrix} s ^ N \\ s ^ { N - 1 } \\ \\ \\ s ^ 0 \end {matrix} \begin {vmatrix} a _ N & a _ { N - 2 } & \cdots & 0 \\ a _ { N - 1 } & a _ { N - 3 } & \cdots & 0 \\ b _ { N - 1 } & b _ { N - 3 } & \cdots \\ c _ { N - 1 } & c _ { N - 3 } & \cdots \\ \cdots \end {vmatrix}$$

که در آن، ضرایب جدید به‌ صورت زیر به‌ دست می‌آیند:

$$\large b _ { N - 1 } = \frac { - 1 } { a _ { N - 1 } } \begin {vmatrix} a _ N & a _ { N - 2 } \\ a _ { N - 1 } & a _ { N - 3 } \end {vmatrix}$$

و

$$\large b _ { N - 3 } = \frac { - 1 } { a _ { N - 1 } } \begin {vmatrix} a _ N & a _ { N - 4 } \\ a _ { N - 1 } & a _ { N - 5 } \end {vmatrix}$$

تکمیل آرایه را تا جایی ادامه می‌دهیم که به سطر $$s^0$$ برسیم.

برای هر سطری که محاسبه می‌کنیم، درایه انتهایی سمت چپ سطر قبلی را عنصر محوری آن می‌نامیم. برای مثال، در سطر $$b$$،‌ عنصر محوری $$a_{N-1}$$ و در سطر $$c$$ عنصر محوری $$b_{N-1}$$ است. برای به‌ دست آوردن هر درایه، حاصل دترمینان زیر را قرینه کرده و بر عنصر محوری تقسیم می‌کنیم:

$$\large \begin {vmatrix} k & m \\ l & n \end {vmatrix}$$

که در آن:

• $$k$$ درایه انتهایی سمت چپ دو سطر بالاتر از سطر فعلی؛
• $$l$$ عنصر محوری؛
• $$m$$ درایه دو سطر بالاتر و ستون سمت راست ستون فعلی؛
• و $$n$$ درایه مشترک یک سطر بالاتر و یک ستون سمت راست درایه فعلی است.

معادله مربوط به درایه مورد نظر به‌ صورت زیر است:

$$\large v = \frac { ( l m ) - ( k n ) } { l }$$

مثال ۱

در این مثال می‌خواهیم مقدار $$C_{N-3}$$ را محاسبه کنیم. ابتدا باید مقادیر $$k$$، $$l$$، $$m$$ و $$n$$ را تعیین کنیم:

• $$k$$ درایه انتهایی سمت چپ دو سطر بالاتر از سطر فعلی است: $$a_{N-1}$$
• $$l$$ عنصر محوری و درایه انتهایی سمت چپ یک سطر بالاتر است: $$b_{N-1}$$
• $$m$$ درایه دو سطر بالاتر و ستون سمت راست ستون فعلی است: $$a_{N-5}$$
• $$n$$ داریه مشترک یک سطر بالاتر و یک ستون سمت راست درایه فعلی است: $$b_{N-5}$$

با قرار دادن مقادیر فوق در فرمول $$C_{N-3}$$، داریم:

$$\large \frac { - 1 } { b _ { N - 1 } } \begin {vmatrix} a _ { N - 1 } & a _ { N - 5 } \\ b _ { N - 1 } & b _ { N - 5 } \end {vmatrix} = \frac { a _ { N - 1 } b _ { N - 5 } - b _ { N - 1 } a _ { N - 5 } } { - b _ { N - 1 } }$$

مثال ۲

در این مثال، پایداری یک سیستم مرتبه‌ سوم را بررسی می‌کنیم که معادله مشخصه آن به‌ صورت زیر است:

$$\large D ( s ) = s ^ 3 + 2 s ^ 2 + 4 s + 3$$

با توجه به این معادله می‌بینیم که دو قاعده اول برقرارند؛ یعنی همه ضرایب غیرصفر و مثبت هستند. بنابراین، آرایه راث را تشکیل می‌دهیم:

$$\large \begin {matrix} s ^ 3 \\ s ^ 2 \\ s ^ 1 \\ s ^ 0 \end {matrix} \begin {vmatrix} 1 & 4 & 0 \\ 2 & 3 & 0 \\ b _ { N - 1 } & b _ { N - 3 } & 0 \\ c _ { N - 1 } & c _ { N - 3 } & 0 \end {vmatrix}$$

ضرایب آرایه بالا به‌ صورت زیر محاسبه می‌شوند:

$$\begin {align*} b _ { N - 1 } & = \frac { ( 2 ) ( 4 ) - ( 1 ) ( 3 ) } { 2 } = \frac { 5 } { 2 } \\ b _ { N - 3 } & = \frac { ( 2 ) ( 0 ) - ( 0 ) ( 1 ) } { 2 } = 0 \\ c _ { N - 1 } & = \frac { ( 3 ) \left ( \frac { 5 } { 2 } \right ) - ( 2 ) ( 0 ) } { \frac { 5 } { 2 } } = 3 \\ c _ { N - 3 } & = \frac { ( 2 ) ( 0 ) - \left ( \frac { 5 } { 2 } \right ) ( 0 ) } { \frac { 5 } { 2 } } = 0 \end {align*}$$

اگر مقادیر بالا را در آرایه قرار دهیم، می‌بینیم که در ستون اول تغییر علامت نداریم و در نتیجه سیستم پایدار است:

$$\large \begin {matrix} s ^ 3 \\ s ^ 2 \\ s ^ 1 \\ s ^ 0 \end {matrix} \begin {vmatrix} 1 & 4 & 0 \\ 2 & 3 & 0 \\ \frac { 5 } { 2 } & 0 & 0 \\ 3 & 0 & 0 \end {vmatrix}$$

حالت‌های خاص

در بررسی معیار پایداری راث هرویتز، ممکن است با مواردی خاص در آرایه مواجه شویم که در ادامه، این حالت‌ها را توضیح می‌دهیم.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

صفر شدن همه درایه‌های یک سطر

اگر همه عناصر یک سطر صفر باشند، از سطر قبلی آن به‌عنوان چندجمله‌ای کمکی استفاده می‌کنیم. به این ترتیب که داریه‌ها، ضرایب چندجمله‌ای کمکی هستند. ریشه‌های معادله کمکی، محل دقیق ریشه‌های مزدوج مختلط را تعیین می‌کنند که روی محور $$j \omega$$ قرار دارند. البته نکته مهم این است که اگر ریشه تکراری روی محور موهومی وجود داشته باشد، سیستم ناپایدار خواهد بود. بنابراین، باید از چندجمله‌ای کمکی برای تعیین تکراری بودن یا نبودن ریشه‌ها استفاده کنیم.

در این فرایند، باید از معادله کمکی نسبت به $$s$$ مشتق گرفت و ضرایب معادله حاصل را با درایه‌های صفر سطر اصلی جایگزین کرد. ادامه آرایه راث با استفاده از مقادیر جدید محاسبه می‌شود.

صفر شدن درایه ستون اول یک سطر

در این حالت خاص، درایه اول یک سطر برابر با صفر است. در این حالت، متغیر کوچک اپسیلن ($$\epsilon$$) را جایگزین صفر کرده و محاسبات را ادامه می‌دهیم. بعد از آنکه کل آرایه تشکیل شد، می‌توانیم مقدار $$\epsilon$$ را به صفر میل داده و مقدار حدی را محاسبه کنیم. اگر علامت درایه بالای $$\epsilon$$ مشابه با علامت درایه زیر آن باشد، یعنی یک ریشه موهومی محض داریم.

مثال ۳

محل ریشه‌های معادله مشخصه زیر را بررسی کنید.

$$\large D (s ) = s ^ 5 + 4 s ^ 4 + 8 s ^ 3 + 8 s ^ 2 + 7 s + 4$$

حل: آرایه راث به صورت زیر است:

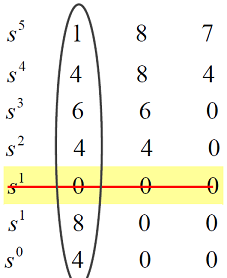
همان‌طور که می‌بینیم، با حالت خاص صفر شدن همه درایه‌های یک سطر مواجه هستیم. بنابراین از معادله کمکی کمک می‌گیریم. همان‌گونه که گفتیم، معادله کمکی را با استفاده از سطر قبل از سطر صفر تشکیل می‌دهیم. بنابراین، معادله کمکی را به صورت زیر می‌نویسیم (به توان‌ها و ضرایب متغیرها در معادله کمکی دقت کنید):

$$\large P (s) = 4 s ^2 + 4 = 0$$

معادله کمکی بالا، دو ریشه روی محور $$j \omega$$ دارد.

اکنون برای آنکه محاسبات مربوط به آرایه راث را ادامه دهیم، از معادله کمکی مشتق گرفته و ضرایب آن را در سطری قرار می‌دهیم که صفر است.

مشتق معادله کمکی به صورت زیر است:

$$\large \frac {d P ( s ) } { d s } = 8 s + 0$$

سطر جدید در آرایه راث بالا نشان داده شده است. می‌بینیم که دو ریشه‌ مزدوج روی محور موهومی، وجود دارد و سایر ریشه‌ها سمت چپ هستند.

مثال ۴

تعداد ریشه‌های سمت راست محور موهومی مربوط به معادله زیر را تعیین کنید.

$$\large q (s ) = s ^ 4 + s ^ 3 + 2 s ^ 2 + 2 s + 3 = 0$$

حل: آرایه راث به صورت زیر است. همان‌طور که می‌بینیم، درایه اول یک سطر صفر شده است. این درایه را با $$\epsilon$$ جایگزین کرده و محاسبات را ادامه می‌دهیم.

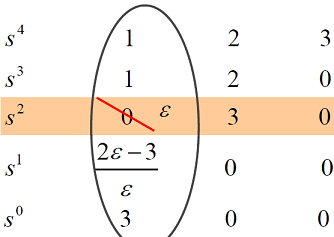
با میل دادن $$\epsilon$$ به صفر، می‌بینیم که دو بار تغییر علامت در ستون اول جدول راث خواهیم داشت. بنابراین، دو ریشه در سمت راست محور موهومی وجود دارد.

مثال ۵

پایداری سیستم حلقه‌ بسته زیر را بررسی کنید.

حل: با توجه به مطالبی که درباره ساده‌سازی نمودارهای بلوکی گفتیم، سیستم بالا به صورت زیر ساده می‌شود:

بنابراین، معادله مشخصه به صورت زیر خواهد بود:

$$\large D ( s ) = s ^ 3 + 10 s ^ 2 + 31 s + 1030$$

آرایه راث را به صورت زیر تشکیل می‌دهیم:

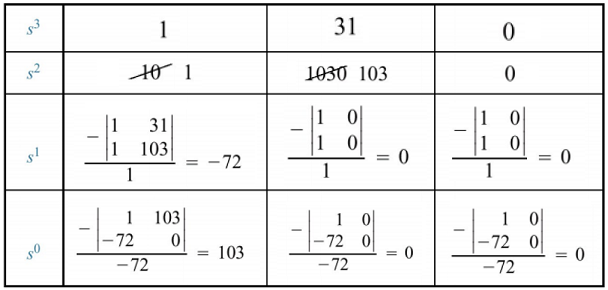
همان‌طور که می‌بینیم، دو تغییر علامت وجود دارد و در نتیجه، سیستم حلقه بسته، دو قطب سمت راست محور موهومی خواهد داشت. بنابراین، سیستم ناپایدار است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سیستم کنترل حلقه باز — به زبان ساده
• مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل — به زبان ساده
• تقلب‌نامه (Cheat Sheet) تبدیل لاپلاس

^^