مجموعه کانتور در نظریه مجموعه | به زبان ساده

در ریاضیات و بخصوص نظریه مجموعه ها، مجموعه کانتور (Cantor Set) از اهمیت زیادی برخوردار است. «توپولوژی نقطه-مجموعه» (Point-set Topology) در بسیاری از موارد وام گرفته از مجموعه کانتور است. از این لحاظ در این نوشته از مجله فرادرس به بررسی مجموعه کانتور در نظریه مجموعه‌ها پرداختیم.

به منظور آشنایی با مجموعه کانتور بهتر است ابتدا نوشتارهای دیگر مجله فرادرس در این زمینه، مانند تابع کانتور و خصوصیات آن و مجموعه بورل در نظریه اندازه | به زبان ساده را بخوانید. همچنین خواندن مطالب عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده و فضای توپولوژیک در ریاضیات — به زبان ساده نیز خالی از لطف نیست.

مجموعه کانتور در نظریه مجموعه

مجموعه کانتور (Cantor Set) مجموعه‌ای از نقاط است که روی یک قطعه خط قرار گرفته و دارای ویژگی‌های قابل توجه و عمیقی هستند. این مجموعه اولین بار توسط «جان اسمیت» (Henry John Stephen Smith) ریاضیدان ایرلندی، در سال 1874 مورد بررسی قرار گرفت ولی بعدها توسط ریاضیدان آلمانی، «کئورگ کانتور» (George Cantor) در سال ۱۸۸۳ در مقاله‌ای ارزیابی شده و خصوصیات جالب توجه آن مرور و بعضی از قضیه‌های مرتبط با آن اثبات گردید.

فیلم آموزش مبانی آنالیز ریاضی در فرادرس

کلیک کنید

هر چند کانتور روش ایجاد مجموعه کانتور را کاملا انتزاعی شرح داده است ولی روش معمول آن، تقسیم پاره خط به سه بخش و برداشتن بخش وسط در هر بار تقسیم‌بندی است. این کار تکرار شده تا به کوچکترین بخش‌ها روی پاره خط برسیم.

این ایده تقسیم‌بندی پاره خط به سه بخش، باعث شده که بتوان مجموعه کانتور را به کمک مجموعه‌ای از «سه تایی‌های کانتور» (Cantor Ternary Set) معرفی کرد. روال تقسیم و حذف در مجموعه کانتور تا جایی ادامه پیدا می‌کند که مفهوم «مجموعه کامل» (Perfect Set) که در هیچ کجا چگال (Nowhere Dense) نیست، ادامه پیدا می‌کند.

در تصویر متحرک ۱، مجموعه کانتور را مشاهده می‌کنید. هر چه به این مجموعه نزدیک‌تر شویم، باز هم خودش را تکرار می‌کند. از این نظر، مجموعه کانتور، شبیه یک فراکتال (Fractal) عمل می‌کند. در تصویر زیر، هر عضو این مجموعه، توسط خطوط عمودی نمایش داده شده است.

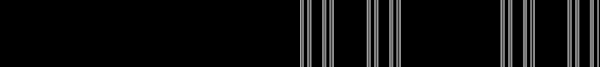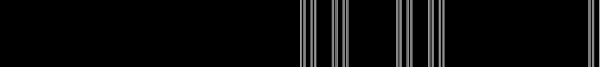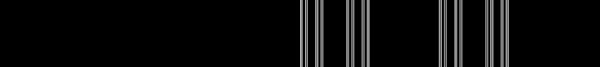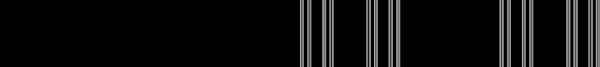
ساختار مجموعه کانتور

همانطور که گفته شد، مجموعه کانتور ($$\cal{C}$$) از تکرار تقسیم‌بندی یک پاره خط به سه بخش و حذف بخش میانی حاصل می‌شود. بازه $$[0,1]$$ را در نظر بگیرید. اگر این پاره خط را به سه بخش مساوی تقسیم کنیم، بازه‌هایی به شکل $$[0,\frac{1}{3}]$$، $$(\frac{1}{3},\frac{2}{3})$$ و $$[\frac{2}{3},1]$$ حاصل می‌شود. با حذف بخش وسطی، خواهیم داشتم:

$$ \large {\mathcal{C}}_1= [ 0,\frac{1}{3}] \cup [ \frac{2}{3}, 1 ] $$

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل مساله در فرادرس

کلیک کنید

حال هر یک از این بخش‌ها را هم به سه قسمت تقسیم کرده و بخش میانی هر یک را حذف می‌کنیم.

$$\large {\mathcal{C}}_2 = [ 0, \frac{1}{9}] \cup [\frac{2}{9},\frac{1}{3}] \cup [ \frac{2}{3}, \frac{7}{9}] \cup [\frac{8}{9},1]  $$

این عمل را بی‌نهایت بار تکرار می‌کنیم. به طوری که در $$n$$امین مرحله مجموعه $$\cal{C_n}$$ به شکل زیر معرفی خواهد شد.

$$ \large {\displaystyle {\mathcal{C}}_{n} = {\frac {{\mathcal{C}}_{n-1}}{3}} \cup \left( { \frac {2}{3}} + { \frac {{\mathcal{C}}_{ n - 1 }}{3}} \right){ \text{ for }} n \geq 1,{ \text{ and }}{\mathcal{C}}_{0} = [ 0 , 1 ]} $$

به این ترتیب، مجموعه سه‌تایی کانتور، شامل همه نقطه‌های بازه $$[0,1]$$ است که حذف نشده‌اند. در هر یک از گام‌ها، $$ {\mathcal {C}}_n$$‌ها با یکدیگر اشتراک‌هایی دارند. اشتراک این مجموعه‌ها، مجموعه کانتور نهایی ($$\cal{C}$$) را تشکیل می‌دهد.

$$ \large {\displaystyle { \mathcal {C}} = \bigcap _{n = 1}^{ \infty } {\mathcal{C}}_{n}} $$

در تصویر ۲، گام‌های ایجاد مجموعه کانتور تا شش مرحله نمایش داده شده.

با استفاده از ایده «تبدیل خود-مشابهت» (Self-similarity Transformation)، می‌توان روابط زیر را برای مجموعه کانتور نوشت:

$$ \large {\displaystyle T_{L}(x)=x/3,\;\;\;\;T_{R}(x)=(2+x)/3} $$

و

$$ \large {\displaystyle {\mathcal {C}}_{n}=T_{L}( {\mathcal {C}}_{n-1})\cup T_{R}( {\mathcal {C}}_{n-1})}$$

به این ترتیب فرمول بسته برای مجموعه کانتور ساخته شده که به شکل زیر خواهد بود.

$$ \large {\displaystyle {\mathcal {C}} = [0,1] \smallsetminus \bigcup _{n = 0}^{ \infty }\bigcup _{k = 0 }^{3^{n} - 1}\left({ \frac {3k + 1}{3^{n + 1 }}},{\frac {3 k + 2 }{3^{ n + 1 }}}\right)}$$

واضح است که قطعه‌های میانی حذف شده نیز فرمی به صورت $$ {\displaystyle \textstyle \left({\frac {3 k + 1}{3^{n + 1}}},{\frac {3 k + 2}{3^{n + 1}}}\right)}$$ خواهند داشت، که از میان فاصله بسته $$ {\displaystyle \textstyle \left[{\frac {3 k + 0}{3^{n + 1}}},{\frac {3 k + 3}{3^{n + 1}}}\right] = \left[{\frac {k + 0}{3^{n}}},{\frac {k + 1}{3^{n}}}\right]}$$ حذف شده است. به این ترتیب مجموعه کانتور را می‌توان به شکل زیر برحسب این فاصله‌ها، مشخص کرد.

$$ \large {\displaystyle {\mathcal {C}}=\bigcap _{n = 1}^{\infty }\bigcup _{k = 0}^{3^{n - 1 } - 1}\left( \left[{ \frac {3 k + 0}{3^{n}}},{\frac {3 k + 1}{3^{n}}}\right]\cup \left[{\frac {3 k + 2}{3^{n}}},{\frac {3 k + 3}{3^{n}}}\right]\right)}$$

همانطور که دیده می‌شود، بخش میانی از تقسیم سه تایی یعنی $$ {\displaystyle \textstyle \left({\frac {3 k + 1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)} $$ از فاصله بسته $$ {\displaystyle \textstyle \left[{\frac {k + 0}{3^{n - 1}}},{\frac {k + 1}{3^{ n - 1}}}\right] = \left[{\frac {3 k + 0}{3^{n}}},{\frac {3 k + 3}{3^{n}}}\right ]} $$ با اشتراک‌گیری از بخش $$ {\displaystyle \textstyle \left[{ \frac {3 k + 0}{3^{n}}}, { \frac { 3 k + 1}{3^{n}}} \right] \cup \left[{ \frac {3 k + 2}{3^{n}}},{ \frac {3 k + 3}{3^{n}}}\right ]}$$ حذف شده است.

روال حذف بخش دوم از تقسیم و ادامه تقسیم بندی، یک مثال از قانون تقسیم متناهی است. همانطور که در تصویر ۴ مشاهده می‌کنید، تقسیم‌بندی‌ها و حذف بخش میانی، تشکیل یک «رشته فراکتال» (Fractal String) را می‌دهد.

بیان مجموعه کانتور بوسیله نمایش اعداد

از نظر مجموعه اعداد می‌توان مجموعه کانتور را به نحوه نمایش اعداد اعشاری برمبنای ۳ مرتبط دانست. اعداد حقیقی در بازه $$[0,1]$$ را در نظر بگیرید که به پایه (Base) یا مبنای ۳ نوشته شده‌اند و برای نمایش آن‌ها لزومی به رقم ۱ در نمایش آن عدد برمبنای ۳ نیست. در حقیقت هر عدد برمبنای ۳، شامل ارقام ۰ و ۱ و ۲ است. توجه داشته باشید که با حذف رقم ۱، انگار که بخش میانی آن را حذف کرده‌ایم.

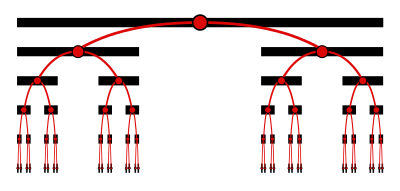
همانطور که در تصویر ۴ مشاهده می‌کنید، یک نقطه در مجموعه کانتور، یک محل یا مسیر منحصر به فرد در نمودار را به خود اختصاص داده است. عمق این درخت باینری (Binary Tree)، بی‌نهایت است. در هر بار تفکیک یا تقسیم، با توجه به حذف بازه میانی، ممکن است جهت حرکت به سمت راست یا چپ باشد. حرکت به سمت راست را با ۲ و حرکت به سمت چپ را با ۰ نمایش می‌دهیم. به این ترتیب اگر با جایگزینی مقادیر ۲ با ۱، رشته عددی جدیدی ایجاد کنیم، در حقیقت یک نگاشت یک به یک و پوشا بین مجموعه کانتور و این درخت باینری بوجود خواهد آمد.

یک تناقض شیرین

روند حذف قسمت میانی و تقسیم‌بندی تکراری بازه $$[0,1]$$ را در قسمت قبلی و البته به کمک روابط گفته شده، مشخص کردیم. با توجه به طول یا اندازه (Measure) قسمت‌های حذف شده در هر مرحله، می‌توانیم رابطه زیر را بنویسیم:

$$ \large \sum_{n = 0}^\infty \frac{2^n}{3^{n + 1}} = \frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81} + \cdots = \frac{1}{3}\left( \frac{1}{1 - \frac{2}{3}}\right) = 1$$

واضح است که رابطه بالا یک تصاعد یا «دنباله هندسی» (Geometric Progression) را نشان می‌دهد. این مجموع برابر با ۱ است. از آنجایی که کل طول بازه نیز برابر با ۱ بوده، به نظر می‌رسد که مجموع طول بخش‌های حذف شده با طول کل فاصله برابر است. به این ترتیب با کمال تعجب به این نتیجه می‌رسیم که هیچ بخشی از قسمت‌های باقی مانده وجود ندارد که طولی بیش از صفر داشته باشد. این امر به نظر یک تناقض می‌رسد.

از طرفی با توجه به روالی که برای حذف کردن نقطه‌ها در نظر گرفتیم، مشخص است که نقاط مرزی فاصله حذف شده، باید در مجموعه باقی مانده باشند. زیرا فاصله‌های حذف شده، به صورت فاصله‌های باز یا مجموعه‌های باز (Open Sets) بودند که شامل نقاط مرزی نیستند. این امر نشان می‌دهد که مجموعه کانتور، یک مجموعه تهی نیست و در اصل شامل بی‌نهایت نقطه است که به صورت تک نقطه (با طول‌هایی برابر با صفر) ظاهر شده‌اند. به این ترتیب تناقض برطرف می‌شود زیرا مجموعه کانتور شامل اعضایی است که اندازه‌ای برابر با صفر دارند.

در ادامه به بررسی چند قضیه در مورد مجموعه کانتور خواهیم پرداخت.

قضیه ا در رابطه با مجموعه کانتور

در این قضیه نشان می‌دهیم که مجموعه کانتور شامل هیچ زیرفاصله‌ای از $$[0,1]$$ نیست. در حقیقت این قضیه بیانگر صفر بودن طول اعضای مجموعه کانتور است.

اثبات: فرض کنید $$[a,b] \subset [0,1]$$ یک بازه اختیاری در فاصله ۰ تا ۱ باشد. نشان می‌دهیم که این زیرفاصله در مجموعه کانتور حضور ندارد یا به بیان دیگر زیر مجموعه‌ای از مجموعه کانتور نیست.

می‌توان مقدار $$a$$ و $$b$$ را با توجه به ویژگی اعداد اعشاری به صورت زیر بر مبنای ۳ نمایش داد.

$$ a = 0.a_1a_2a_3\cdots_3 $$

$$ b = 0.b_1b_2b_3\cdots_3 $$

با توجه به تعریفی که برای اعداد و اعضای مجموعه کانتور بیان کردیم، اگر بعضی از ارقام $$a_i$$ برابر با ۱ باشند، عدد $$a$$ درون مجموعه کانتور $$\cal{C}$$ نیست. همین وضعیت نیز برای عدد $$b$$ وجود دارد. به همین علت آخرین رقم اعداد $$a$$ و $$b$$ را با رقم ۱ بیان می‌کنیم تا مطمئن شویم که در مجموعه کانتور حضور ندارند.

حال $$k$$ را کوچکترین اندیسی در نظر بگیریم که در آن $$a_k \neq b_k$$. به این ترتیب برای مجموعه کانتور باید $$a_k =0  , b_k =2$$ باشد. در نتیجه

$$ \large 0.a_1a_2a_3\cdots a_{k - 1}1_3 \in [a,b] $$

به این ترتیب نتیجه می‌گیریم که $$[a,b]$$ زیرمجموعه $$\cal{C}$$ نیست.

قضیه ۲ در رابطه با مجموعه کانتر

مجموعه کانتور ناشمارا (Uncountable) است.

اثبات: تابع $$f$$ را به صورت زیر در نظر بگیرید.

$$ \large f : {\cal{C}} \rightarrow [0,1] $$

که برای عدد $$x = 0.x_1x_2x_3\cdots_3$$ متعلق به مجموعه کانتور $$\cal{C}$$ به شکل زیر محاسبه می‌شود.

$$ \large f(x) = 0 .(x_1/2)(x_2/2)(x_3/2) \cdots _2 $$

به بیان دیگر تابع $$f$$ بست سه گانه $$x$$ را به شکلی تغییر می‌دهد که رقم ۲ به ۱ تبدیل شده و عدد به مبنای ۲ درمی‌آید. می‌توان نشان داد که چنین تابعی یک تابع یک به یک و پوشا است در نتیجه معکوس‌پذیر است. از آنجایی که برای هر عضو دلخواه از بازه $$[0,1]$$ مثل $$y$$ داریم:

$$ \large y = f(0.(2y_1)(2y_2)(2y_3) \cdots_3) = y $$

بطوری که $$y = 0.y_1y_2y_3\cdots_2\in [0,1]$$. حال در نظر بگیرید که مجموعه $$\cal{C}$$، شمارا است و اعضای آن را به صورت زیر در نظر بگیرید.

$$ \large \mathcal{C} = \{ c_{1},c_{2},c_{3},\cdots \} $$

برای هر $$y \in [0,1]$$، تابع $$g(y)$$ را برابر با اندیس $$j$$ از عنصر $$c_j$$ فرض کنید که برای آن $$f(c_j) = y $$.

به این ترتیب می‌توان دنباله‌ای به شکل $$\{d_i\}_{i \in N}$$ در نظر گرفت که برای هر $$y \in [0,1]$$ داشته باشیم $$d_g(y) = y$$. این موضوع یک تناظر یک به یک بین مجموعه اعداد طبیعی و فاصله $$[0,1]$$ ایجاد می‌کند که نشان می‌دهد بازه $$[0,1]$$، شمارا است، که تناقض محسوب می‌شود؛ زیرا می‌دانیم در این بازه، ناشمارا عدد، وجود دارد.

خصوصیات و ویژگی‌های مجموعه کانتور

با توجه به نحوه ساخت مجموعه کانتور، ویژگی و خصوصیات جالبی برای این مجموعه وجود دارد که در ادامه این متن به چند نمونه از آن‌ها خواهیم پرداخت.

فیلم آموزش مبانی آنالیز ریاضی – مرور، حل مثال و تست کنکور ارشد – بخش یکم در فرادرس

کلیک کنید

عدد اصلی یا کاردینالیتی مجموعه کانتور

همانطور که مشخص شد، بی‌اندازه نقطه در مجموعه کانتور در بازه $$[0,1]$$ وجود دارد. عدد اصلی برای مجموعه $$\cal{C}$$ برابر با $$2^{\aleph_0}$$ است. البته می‌دانیم که مجموعه نقاط انتهایی بازه‌های حذف شده، شمارش‌پذیر هستند ولی تعداد اعداد در مجموعه کانتور که نقطه انتهای فاصله‌ها نیستند، شمارش‌ناپذیر است.

همانطور که گفته شد، در مجموعه کانتور، هیچ فاصله‌ای با اندازه یا طول صفر وجود ندارد. این ویژگی را در مجموعه اعداد گنگ نیز می‌توان در نظر گرفت با این تفاوت که مجموعه اعداد گنگ، چگال (Dense) در هر بازه هستند ولی مجموعه اعداد کانتور در هیچ فاصله‌ای، چگال نیست.

نکته: یک زیر مجموعه $$A$$ از فضای توپولوژیک $$X$$، چگال یا فشرده در $$X$$ است اگر برای هر نقطه $$x \in X$$ یک همسایگی شامل $$x$$ وجود داشته باشد که حداقل شامل یک نقطه باشد. به بیان دیگر، اشتراک $$A$$ با هر زیر مجموعه باز غیر تهی از $$X$$، ناتهی باشد.

هم‌-شبیه در مجموعه کانتور

مجموعه کانتور، یک الگو و طرح برای ایجاد ساختار فراکتال‌ها است. مجموعه کانتور دارای خاصیت «هم‌-شبیه» (Self-similar) است. به این معنی که هر مجموعه کانتور با کپی خود برابر است. این امر نشانگر آن است که هر مجموعه کانتور با تبدیل‌های خود-مشابهت راست ($$T_R$$) و چپ ($$T_L$$) خود برابر است.

$$ \large T_L(x) = x /3 $$

$$ \large T_R (x) = (2 + x) /3$$

پس مجموعه کانتور نسبت به تبدیل هم‌ریخت،‌ ناوردا (Invariant) است.

$$ \large {\displaystyle T_{L}({\mathcal {C}})\cong T_{R}({\mathcal {C}})\cong {\mathcal {C}}=T_{L}({\mathcal {C}})\cup T_{R}({\mathcal {C}})}$$

با تکرار دوباره تشکیل تبدیلات $$T_L$$ و $$T_R$$ می‌توان یک درخت باینری نامتناهی را به تصویر بکشد. در این درخت، هر گره، ممکن است منشاء یک زیر درخت به سمت چپ یا راست باشد.

اندازه و فضای احتمال

به مجموعه کانتور می‌توان به چشم دنباله‌های باینری از گروه‌های فشرده (Compact Group) نگریست. به این ترتیب می‌توان آن را به شکل یک «اندازه هار» (Haar Measure) در نظر گرفت. در صورتی که این اندازه را نرمال کرده و در بازه ۰ تا ۱ قرار دهیم، دارای خصوصیات یک تابع احتمال خواهد بود و می‌توان آن را به عنوان یک مدل احتمال برای پرتاب بی‌نهایت بار یک سکه در نظر گرفت.

از منظر نظریه اندازه لبگ، مجموعه کانتور، یک مثال از مجموعه‌ای است که دارای ناشمارا عضو بوده ولی اندازه آن صفر است.

خصوصیات عددی اعضای مجموعه کانتور

اگر اعضای مجموعه کانتور را به صورت اعداد در بازه ۰ و ۱ در نظر بگیریم، واضح است که:

• هر عدد در فاصله $$[0,2]$$ توسط مجموعه دو عدد کانتور،‌ قابل نمایش است.
• بین هر دو عدد کانتور، حتما یک عدد غیرکانتور، وجود دارد.

ذرات کانتور

اگر مجموعه کانتور را در حالت چند بعُدی تصویر کنیم، حاصل یک مجموعه شامل «ذرات کانتور» (Cantor Dust) خواهد بود. به این ترتیب اگر ضرب دکارتی مجموعه کانتور در خودش را در نظر بگیریم، یک فضای کانتور حاصل می‌شود.

مشابه مجموعه کانتور، ذرات کانتور نیز دارای اندازه صفر هستند. مشابه ذرات کانتور، «فرش کانتور» (Cantor Carpet) نیز در حالت دو بعدی ساخته می‌شود که در آن هر مربع به ۹ بخش مساوی تقسیم شده و بخش میانی آن حذف می‌شود.

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل تست کنکور ارشد – بخش دوم در فرادرس

کلیک کنید

این تقسیم‌بندی ادامه می‌یابد. در تصویر ۶، نمونه‌ای از فرش کانتور که گاهی به آن «فرش سیرپینکسکی» (Sirepinkski Carpet) نیز گفته می‌شود،‌ نمایش داده شده است.

تاریخچه مجموعه کانتور

مجموعه کانتور در ابتدای امر توسط جورج کانتور به روشی کلی و انتزاعی تعریف گردید و از ساختار و تشکیل بازه‌های سه گانه فقط به صورت گذرا استفاده شد. ایده اصلی کانتور ایجاد یک مجموعه کامل بود که در هیچ‌ نقطه‌ای متراکم یا چگال نیست. همچنین در مقاله اصلی او، چندین ساختار متفاوت از مفهوم انتزاعی مرتبط با مجموعه کانتور ارائه گردید. این مجموعه در زمانی که کانتور آن را ابداع کرد ، انتزاعی و غیر قابل تصور، تلقی می‌شد. کانتور خود از کسانی بود که اعتقاد داشت این دنباله از تقسیمات سه گانه، همگرا نیستند. ولی مشخص شدن وجود نقطه همگرایی برای این دنباله از اعداد، او را در توسعه انتزاع و تئوری عمومی مجموعه‌های نامتناهی ترغیب کرد.

خلاصه و جمع‌بندی

در این متن به بررسی مجموعه کانتور در نظریه مجموعه‌ها و بخصوص نحوه تشکیل آن و همچنین بعضی از ویژگی‌های آن پرداختیم. همانطور که مشخص شد، این مجموعه هر چند دارای رفتار بسیار پیچیده‌ای است ولی روش ساخت آن بسیار ساده است. در اکثر اوقات به علت ویژگی‌های جالب مجموعه کانتور از آن برای ایجاد مثال نقض در بسیاری از قضیه‌ها یا تئوری‌های مرتبط با نظریه مجموعه‌ها استفاده می‌کنند. همچنین از ساختار مجموعه کانتور به منظور ایجاد ساختار فراکتال نیز می‌توان استفاده کرد. همانطور که خواندید، در فضاهای چند بعدی نیز مجموعه کانتور قابل تعریف و استفاده است.