تابع کانتور و خصوصیات آن | به زبان ساده
تابع کانتور (Cantor Function) به عنوان یک تابع با رفتار عجیب در ریاضیات برای بیان بسیاری از مثالهای نقض به کار میرود. برعکس یک تابع هموار و پیوسته، تابع کانتور جهشهای سریع و ناهمواریهای زیادی دارد و رفتار پیچیده و پر از رمز و راز نشان میدهد که پیوسته (Continuous) بوده ولی «مطلقا پیوسته» (Absolute Continuous) نیست. از این جهت که تابع کانتور در ریاضیات مدرن و بخصوص نظریه مجموعهها و نظریه اندازه بسیار کاربرد دارد، این نوشتار از مجله فرادرس را به تابع کانتور و خصوصیات آن اختصاص دادهایم.
برای آشنایی بیشتر با مفهوم تابع و پیوستگی، ابتدا نوشتارهای پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده و قضیه تفکیک لبگ در نظریه اندازه — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب نظریه اندازه در ریاضیات — مفاهیم و کاربردها و قضیه رادون نیکودیم و اثبات آن — به زبان ساده نیز خالی از لطف نیست.
تابع کانتور و خصوصیات آن
تابع کانتور (Cantor Function) و مجموعه کانتور (Cantor Set) هر دو پیچیده و رفتار نامشخصی دارند بطوری که نحوه ساخت هر یک از آنها به شکلهای گوناگون میسر است. هر چند تابع کانتور همه جا (Everywhere) پیوسته است ولی مشتق آن، تقریبا همهجا (Almost Everywhere) صفر است. در ادامه به روشی برای تولید تابع کانتور اشاره خواهیم کرد.
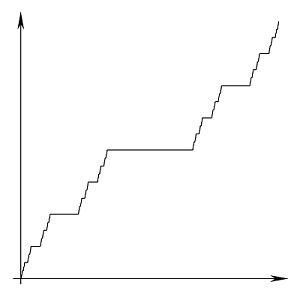
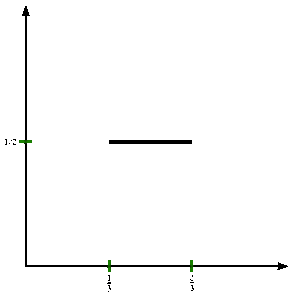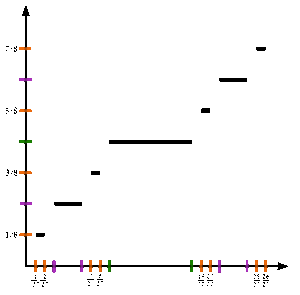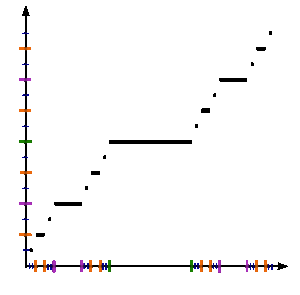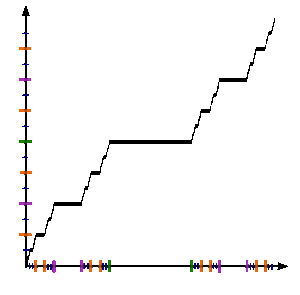
در تصویر ۱، نمودار تابع کانتور را در بازه ۰ تا ۱ مشاهده میکنید. چنین تابعی را گاهی «تابع لبگ» (Lebesgue Function)، «تابع کانتور-ویتالی» (Cantor-Vitali Function) یا «پلکان شیطان» (Devil's Staircase) نیز مینامند.
این تابع توسط «گئورگ کانتور» (Georg Cantor)، ریاضیدان آلمانی در سال 1884 طی مقالهای، معرفی شد. این تابع به عنوان یک مثال نقض در مورد «قضیه اساسی حسابان» (Fundamental Theorem of Calculus) به کار گرفته میشود. در ادامه متن به همان روشی که جورج کانتور تابع معروف خود را معرفی کرد، گامهای تولید تابع کانتور را بر میداریم.
همانطور که گفته شد، معمولا تابع کانتور را در بازه $$[0,1]$$ تعریف میکنند. به این ترتیب اگر چنین تابعی را با $$c(x)$$ نشان دهیم، دامنه و برد آن به شکل زیر خواهد بود.
$$ \large c : [0,1] \rightarrow [0,1]$$
مشخص است که دامنه و برد این تابع، بازه $$[0,1]$$ است. برای تعیین یا تعریف تابع کانتور در این بازه، روال زیر را در نظر میگیریم.
- عدد $$x$$ را برمبنای یا پایه ۳ نمایش دهید. در نتیجه عدد در دامنه این تابع با ارقام صفر، یک و دو (0,1,2) نمایش داده خواهند شد.
- اگر $$x$$ شامل رقم ۱ بود، تمامی ارقام بعد از آن را با صفر جایگزین کنید.
- همچنین تمامی ارقام ۲ که در باقیمانده ارقام قرار دارند، را با ۱ جایگزین نمایید.
- عدد حاصل را به صورت یک عدد باینری (برمبنای ۲) بخوانید. این عدد همان مقدار تابع کانتور برای $$x$$ است.
برای مثال فرض کنید که مقدار تابع کانتور را در $$\frac{1}{4}$$ محاسبه کنیم.
- $$\frac{1}{4}$$ برمبنای ۳ به صورت $$0.02020202\ldots$$ نوشته میشود.
- از آنجایی که هیچ رقم ۱ در آن دیده نمیشود، گام بعدی را اجرا میکنیم.
- همه ارقام ۲ در عدد مذکور را به ۱ تبدیل میکنیم.
- عدد حاصل به شکل $$0.01010101\ldots$$ در آمده که بیانگر $$\frac{1}{3}$$ برمبنای ۱۰ است. پس $$c(\frac{1}{4}) = \frac{1}{3}$$.
به منظور روشنتر شدن موضوع، همین عملیات را برای عدد $$\frac{1}{5}$$ نیز به کار میبریم.
- نمایش عدد $$\frac{1}{5}$$ برمبنای ۳ به صورت $$0.01210121\ldots$$ خواهد بود.
- همه ارقام بعد از اولین ۱ را به صفر تبدیل میکنیم. به این ترتیب حاصل به شکل $$ 0.010000\ldots$$ درخواهد آمد.
- از آنجایی که هیچ رقم ۲ در این عدد دیده نمیشود، تغییری در عدد حاصل نمیشود.
- نمایش برمبنای ۲ این عدد به صورت $$\frac{1}{4}$$ است. در نتیجه $$c(\dfrac{1}{5}) = \frac{1}{4}$$.
این بار عدد $$\frac{200}{243}$$ را در نظر بگیرید.
- نمایش این عدد برمبنای ۳ به صورت $$0.21101222\ldots$$ است.
- همه ارقام بعد از اولین ۱ را به صفر تبدیل میکنیم. پس عدد به صورت $$0.21$$ در خواهد آمد.
- در عدد حاصل، رقم ۲ را نیز به ۱ تبدیل خواهیم کرد.
- پس عدد برمبنای ۲ به شکل $$0.11$$ نوشته میشود که در مبنای ۱۰ به صورت $$\frac{3}{4}$$ محاسبه میگردد. پس $$c(\frac{200}{243}) = \frac{3}{4}$$.
به این ترتیب میتوان با توجه به مفهوم «مجموعه کانتور» (Cantor Set)، تابع کانتور را به صورت زیر تعریف کرد.
$$ \large {\displaystyle c(x) = { \begin{cases}\sum _{ n = 1 }^{ \infty }{\frac { a_{ n } }{ 2^{ n } }} , & x = \sum _{n = 1}^{\infty }{\frac {2 a_{n}}{3^{ n } }} \in {\mathcal {C}}\ \mathrm { for } \ a_{n}\in \{0,1\}; \\ \sup _{y \leq x, \, y \in {\mathcal {C}}} c(y) , & x \in [ 0 , 1 ] \setminus {\mathcal {C}}\\ \end{cases}}}$$
رابطه بالا، یک فرمول خوش-تعریف (Well-Define) است زیرا بیان هر عدد برمبنای ۳، منحصر به فرد بوده و فقط شامل ارقام ۰ تا ۲ است. از طرفی چون $$c(0)=0 , c(1) = 1$$ تابع $$c$$ یک تابع یکنوا روی مجموعه کانتور $$\mathcal{C}$$ است. واضح است که برای هر مقداری مثل $$x \in [0,1] \backslash \mathcal{C}$$ نیز رابطه $$0 \leq c(x) \leq 1 $$ برقرار است.
اگر برای همه مقادیر در بازه $$[0,1]$$ محاسبات گفته شده را اجرا کنیم، به نمودار تابع کانتور خواهیم رسید. در تصویر ۲، نحوه تشکیل نمودار تابع کانتور به نمایش در آمده است. همانطور که میبینید، این تابع دارای پرشهایی است که در تک نقطههایی با اندازه صفر رخ میدهند. بنابراین در عین حال که تابعی پیوسته است، مطلقا پیوسته نیست.
ویژگیهای اصلی تابع کانتور
با توجه به ویژگیهایی که تعریف تابع کانتور در بر دارد، رفتار آن بسیار متفاوت با توابع معمول و خوشتعریف است. در این قسمت به بعضی از خصوصیات جالب تابع کانتور خواهیم پرداخت.
تابع کانتور و پیوستگی مطلق
یکی از ویژگیهای جالب تابع کانتور، ناپیوستگی مطلق یا نداشتن خاصیت «مطلقا پیوسته» (Absolute Continuity) است. از آنجایی که «اندازه لبگ» (Lebesgue Measure) روی مجموعه نامتناهی شمارشناپذیر کانتور برابر با صفر است، برای هر $$0 < \epsilon <1$$ و $$\delta$$ مثبت، یک دنباله متناهی از زیرفاصلههای مجزا وجود دارد که مجموع طولشان کمتر از $$\delta$$ است، ولی مجموع طول تابع کانتور آنها از $$\epsilon$$ بیشتر است. در نتیجه تابع کانتور مطلقا پیوسته نیست.
پس اگر زیرفاصلههای مجزا را به صورت $$(x_k,y_k)$$ درون $$[0,1]$$ در نظر بگیریم، برای هر $$\delta>0$$ اگر داشته باشیم:
$$ \large { \displaystyle \sum \limits _{k = 1}^{M}(y_{k} - x_{k})< \delta } $$
آنگاه
$$ \large { \displaystyle \sum \limits _{k = 1}^{M} (c ( y_{k} ) - c ( x_{k} )) = 1 } $$
تابع منفرد
تابع کانتور یک نمونه استاندارد از توابع منفرد (Singular Function) محسوب میشود. تابعی $$f$$ را منفرد میگویند اگر دارای خواص زیر باشد:
- تابع $$f$$ روی بازه $$[a,b]$$ پیوسته باشد.
- روی مجموعهای از نقاط آن مثل $$N$$ که دارای اندازه صفر هستند، مشتقپذیر بوده ولی در خارج از آن $$f'(x)$$ موجود نیست. این موضوع بیانگر آن است که تقریبا همه جا (Almost everywhere) مشتق تابع منفرد، صفر است.
- تابع $$f$$ در بازه $$[a,b]$$ ثابت نیست.
همانطور که در نمودار مربوط به تصویر ۱ و تعریف تابع کانتور مشاهده کردید، خواص تابع منفرد برای آن برقرار بوده در نتیجه تابع کانتور یک تابع منفرد است.
تابع توزیع تجمعی احتمال
از تابع کانتور به عنوان تابع توزیع تجمعی ۱/۲-۱/۲ در اندازه برنولی (Bernoulli Measure) روی تکیهگاه مجموعه کانتور استفاده میکنند. در این حالت تابع کانتور به صورت زیر نوشته میشود:
$$ \large c(x) = \mu([0,x])$$
این توزیع احتمال، به توزیع کانتور (Cantor Distribution) معروف است و هیچ قسمت گسسته ندارد. همین امر نشانگر آن است که تابع کانتور دارای نقاط ناپیوستگی نیست و نقاط ناپیوستگی در تک نقطهها و با اندازه صفر رخ میدهد.
قضیه اساسی حسابان
در حساب دیفرانسیل و انتگرال (حسابان) قضیه اساسی حسابان که گاهی به آن قضیه اصلی حساب دیفرانسیل و انتگرال (Fundamental theorem of calculus) نیز گفته میشود، نقش اساسی در ارتباط بین مشتق و انتگرال ایفا میکند.
در این قضیه، بیان میشود که اگر تابع $$f$$ انتگرالپذیر باشد و $$F$$ پادمشتق آن در نظر گرفته شود که پیوسته است، آنگاه:
$$ \large \int_a^b f(x) dx = F(b) - F(a) , \; \; F'(x) =f(x)$$
در حالیکه برای تابع کانتور چنین چیزی برقرار نیست. در حقیقت از آنجایی که تابع کانتور برای هر نقطهای که متعلق به مجموعه کانتور نباشد، مقدار ثابتی دارد، میتوان یک خط موازی محور افقی برایش ترسیم کرد. به این معنی که مشتق در آن نقطه برابر با صفر است. از آنجایی که این اتفاق به جز در نقطههایی با اندازه صفر، رخ میدهد میگوییم مشتق تابع کانتور تقریبا همه جا (Almost Everywhere) صفر است.
ولی از طرفی این تابع در بازههایی متعلق به مجموعه کانتور دارای پرش عمودی است در نتیجه مشتق در چنین وضعیتی وجود ندارد یا بینهایت است. بنابراین باید قضیه اصلی حسابان را برای توابع تقریبا همه جا مشتقپذیر و مطلقا پیوسته به کار برد.
تعریفی دیگر برای تابع کانتور
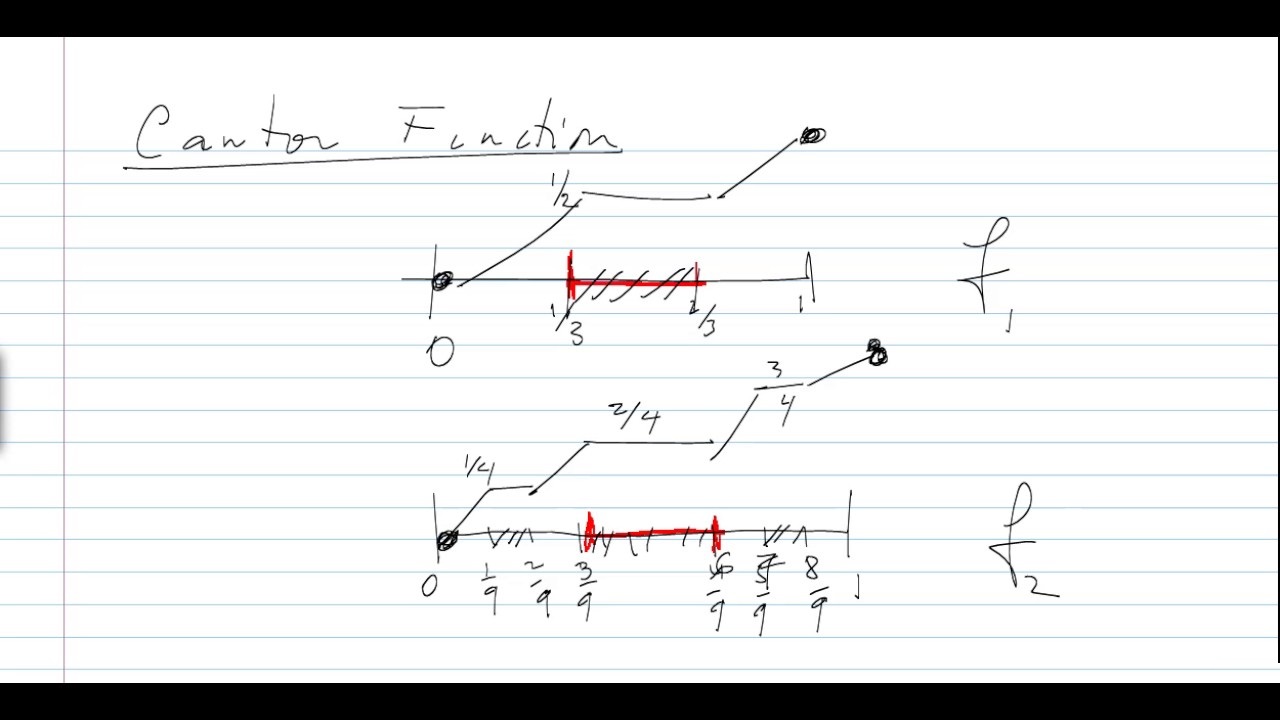
در این قسمت با تعریف دنبالهای از توابع $$\{f_n\}$$ در بازه $$[0,1]$$ که به سمت تابع کانتور میل میکند، گزاره دیگری برای مشخص کردن تابع کانتور معرفی میکنیم.
- اولین جمله دنباله را به صورت $$f_0(x) = x$$ انتخاب میکنیم. به این ترتیب برای هر عدد صحیحی مثل $$n\geq 0 $$ تابع یا عضو بعدی دنباله به صورت زیر تعریف میشود.
- اگر $$0 \leq x \leq \frac{1}{3}$$ آنگاه $$f_{n+1}(x) = \frac{1}{2} \times f_n(3x)$$.
- اگر $$\frac{1}{3} \leq x \leq \frac{2}{3}$$ آنگاه $$f_{n+1}(x) = \frac{1}{2}$$.
- همچنین برای مقادیری که در بازه $$\frac{2}{3} \leq x \leq 1 $$ هستند دنباله تابع به شکل $$f_{n+1} = \frac{1}{2}+\frac{1}{2} \times f_n(3x-2)$$ خواهد بود.
تعریف ارائه شده در نقاط انتهایی $$\frac{1}{3}$$ و $$\frac{2}{3}$$ سازگار است، زیرا به کمک استقرا برای $$n$$ میتوان نشان داد که $$f_n(0) = 0 $$ و $$f_n(1) = 1$$ است.
چیزی که باید مورد بررسی قرار گیرد، همگرایی نقطه به نقطه برای $$f_n$$ به تابع کانتور است که در تعریف قبلی ارائه شد.
با توجه به تعریف جدید برای دنباله توابع میتوان روابط زیر را در نظر گرفت.
$$ \large \max_{x \in [0, 1]} |f_{n+1}(x) - f_n(x)| \le \frac 1 2 \, \max_{x \in [0, 1]} |f_{n}(x) - f_{n-1}(x)|, \quad n \ge 1$$
اگر $$f$$ حد دنباله $$f_n$$در نظر گرفته شود، آنگاه برای هر $$n \geq 0 $$ خواهیم داشت:
$$ \large \max_{x \in [0, 1]} |f(x) - f_n(x)| \le 2^{-n+1} \, \max_{x \in [0, 1]} |f_1(x) - f_0(x)| $$
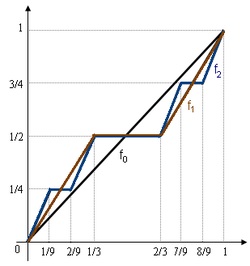
این دنباله و همگرایی آن به تابع کانتور در تصویر ۳ دیده میشود. همانطور که مشخص است با افزایش $$n$$، این تابع به سمت $$c(x)$$ میل خواهد کرد.
خلاصه و جمعبندی
در این متن به تابع کانتور و خصوصیات آن توجه کردیم. ابتدا نحوه تعریف تابع کانتور مورد اشاره قرار گرفت و سپس خصوصیات آن را بررسی نمودیم. همانطور که دیدید، تابع کانتور در ارتباط مستقیم با مجموعه کانتور قرار دارد. با توجه به خصوصیات ویژهای که تابع کانتور دارد، از آن برای ایجاد مثال نقض برای مسائل مربوط به نظریه اندازه و حساب دیفرانسیل و انتگرال استفاده میشود. از این جهت چنین تابعی اهمیت زیادی دارد. نمودارهای ترسیم شده در این نوشتار نیز تغییرات ناگهانی این تابع را معرفی میکنند.










