قضیه پوئینتینگ (Poynting’s Theorem) – به زبان ساده

در راستای تکمیل مجموعه مقالات مجله فرادرس در حوزه الکترومغناطیس، در نظر داریم تا با زبانی ساده به بیان قضیه پوئینتینگ (Poynting’s Theorem) و نحوه به دست آوردن معادله آن بپردازیم.

قضیه پوئینتینگ

در فیزیک الکتریسیته و مغناطیس و به طور کلی نظریه الکترومغناطیسی، قضیه پوئینتینگ بیان کننده پایستگی انرژی (Conservation of Energy) در میدان‌های الکتریکی و مغناطیسی است. می‌توان قضیه پوئینتینگ را مشابه قضیه کار و انرژی در فیزیک مکانیک دانست که از لحاظ فرمول‌بندی ریاضی همانند معادله پیوستگی است.

به عبارت دیگر، قضیه پوئینتینگ تغییرات انرژی ذخیره شده در میدان‌های الکترومغناطیسی را به کار انجام شده روی چگالی بار الکتریکی و شار انرژی مربوط می‌کند. قضیه مذکور به افتخار نام فیزیکدان بریتانیایی «جان هنری پوئینتینگ» (John Henry Poynting) به این نام موسوم شد.

در ادامه این مطلب با ما همراه باشید تا با نحوه به دست آوردن فرم دیفرانسیلی قضیه پوئینتینگ آشنا شویم.

انرژی الکترومغناطیسی

همان‌طور که در مقاله «انرژی موج — از صفر تا صد» دیدیم، میدان‌های الکتریکی و مغناطیسی هر دو می‌توانند انرژی را در خود ذخیره کنند. این انرژی به صورت چگالی انرژی در واحد حجم تعریف می‌شود. چگالی انرژی الکتریکی و چگالی انرژی مغناطیسی به صورت زیر بیان می‌شوند:

$$\large u_{e} = \frac{1}{2} \varepsilon_{0} E^{2}$$
(1)

$$\large u_{m} = \frac{1}{2 \mu_{0}} B^{2}$$
(2)

بیان کردیم که انرژی الکترومغناطیسی به صورت چگالی انرژی بیان می‌شود. پس انرژی کل از گرفتن انتگرال حجمی چگالی‌های انرژی الکتریکی و مغناطیسی به دست می‌آید. یعنی:

$$\large U_{em} = \int_{V} (u_{e} + u_{m})dV = \int_{V} (\frac{1}{2} \varepsilon_{0} E^{2} + \frac{1}{2 \mu_{0}} B^{2})dV$$
(3)

دقت داشته باشید که غالباً در الکترومغناطیس از حرف بزرگ $$U$$ برای نمایش انرژی کل الکترومغناطیسی و از حرف کوچک $$u$$ برای نمایش چگالی انرژی استفاده می‌کنند. مقدار انرژی فوق، در واقع بیانگر مجموع کار، برای جمع‌آوری توزیع بار الکترواستاتیکی در مقابل دافعه کولنی (Coulomb repulsion) و کار لازم برای تولید جریان در برابر نیروی ضد محرکه الکتریکی ست. همچنین توجه داشته باشید که انرژی در کل حجم توزیع شده است.

کار و نیرو لورنتس

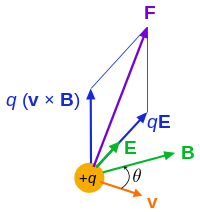
در مقاله «نیروی لورنتس (Lorentz Force) — از صفر تا صد» با نیروی الکترومغناطیسی لورنتس آشنا شدیم و دیدیم که به ذره باردار $$q$$ که با سرعت $$v$$ در یک میدان الکترومغناطیسی حرکت می‌کند، نیروی زیر وارد می‌شود.

$$\large F = q (E +v \times B)$$
(4)

از فیزیک پایه به یاد داریم که کار (ماهیت انرژی) بر حسب ژول، برابر با حاصل ضرب نقطه‌ای نیرو در جابه‌جایی است. یعنی:

$$\large dW = F.dl$$
(5)

در اینجا $$F$$ همان نیرو لورنتس است. $$dl$$ که جز دیفرانسیلی طول (جابه‌جایی) است را می‌توان به صورت حاصل ضرب سرعت در زمان به شکل زیر نوشت:

$$\large dW = F.dl = q(E + v \times B).vdt = qE.vdt$$
(6)

از رابطه فوق مشخص است که تنها میدان الکتریکی می‌تواند کار انجام دهد. به یاد داشته باشید که کار میدان مغناطیسی صفر است.

چگالی جریان الکتریکی و بار الکتریکی به صورت زیر هستند:

$$\large q = \rho V$$
(7)

$$\large J = \rho v$$
(8)

با توجه به دو رابطه فوق، معادله (6) به صورت زیر در می‌آید:

$$\large \frac{\text{d}W}{\text{d}t} = \int_{V}(E.J)dV$$
(9)

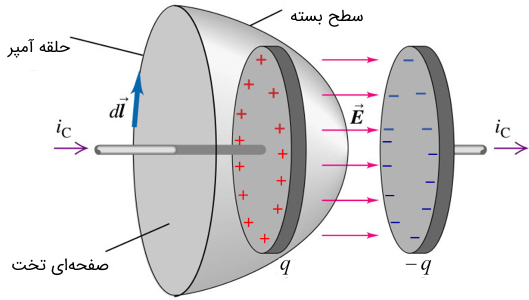
استفاده از قانون آمپر-ماکسول

در مقاله «قانون آمپر -- به زبان ساده» با تعمیم قانون آمپر که به قانون آمپر-ماکسول نیز موسوم است، آشنا شدیم. فرم دیفرانسیلی قانون مذکور به صورت زیر است:

$$\large \triangledown \times B = \mu_{0} J + \mu_{0} \varepsilon_{0} \frac{\partial E}{\partial t}$$
(10)

جمله $$J$$ جریان رسانشی و جمله $$\frac{\partial E}{\partial t}$$ جریان جابه‌جایی را توصیف می‌کند.

با توجه به رابطه (۱۰)، $$J$$ را می‌توان به صورت زیر نوشت:

$$\large J = \frac{1}{\mu_{0}} (\triangledown \times B) - \varepsilon_{0}\frac{\partial E}{\partial t}$$
(11)

برای تشکیل جمله داخل انتگرال در رابطه (9)، نیاز است تا بردار $$E$$ را در معادله فوق ضرب نقطه‌ای کنیم. یعنی:

$$\large E.J = E.[\frac{1}{\mu_{0}} (\triangledown \times B) - \varepsilon_{0}\frac{\partial E}{\partial t}]$$
(12)

$$\large \Rightarrow E.J = \frac{1}{\mu_{0}} (E. (\triangledown \times B)) - \varepsilon_{0} E.\frac{\partial E}{\partial t}$$
(13)

استفاده از قانون القای فارادی

در مقاله «القای فارادی — به زبان ساده» با قانون فارادی آشنا شدیم. همچنین در مقاله «فرم دیفرانسیلی معادلات ماکسول -- به زبان ساده» دیدیم که فرم دیفرانسیلی آن به شکل زیر است.

$$\large \triangledown \times E = - \frac{\partial B}{\partial t}$$
(14)

فیلم آموزش الکترومغناطیس مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

جهت ادامه کار، به سراغ روابط برداری می‌رویم. برای هر بردار دلخواه $$E$$ و $$B$$ رابطه زیر برقرار است.

$$\large \triangledown . (E \times B) = B . (\triangledown \times E) - E . (\triangledown \times B)$$
(15)

حال با فرض اینکه دو بردار $$E$$ و $$B$$ همان میدان‌های الکتریکی و مغناطیسی هستند، به راحتی حاصل (معادل) جمله $$E . (\triangledown \times B)$$ در معادله (13)، با استفاده از رابطه ریاضی (15) و قانون فارادی به دست می‌آید. یعنی:

$$\large E . (\triangledown \times B) = - \triangledown . (E \times B) - B . \frac{\partial B}{\partial t}$$
(16)

با جایگذاری رابطه فوق در معادله (13) داریم:

$$\large E.J = \frac{1}{\mu_{0}} (- \triangledown . (E \times B) - B . \frac{\partial B}{\partial t}) - \varepsilon_{0} E.\frac{\partial E}{\partial t}$$
(17)

همچنین می‌توانیم حاصل ضرب نقطه‌ای برداری‌های $$E$$ و $$B$$ در مشتق‌های زمانیشان را به صورت زیر بنویسیم:

$$\large B . \frac{\partial B}{\partial t} = \frac{\partial}{\partial t} (\frac{1}{2} B^{2})$$
(18)

$$\large E . \frac{\partial E}{\partial t} = \frac{\partial}{\partial t} (\frac{1}{2} E^{2})$$
(19)

با توجه به دو رابطه فوق، رابطه (17) به صورت زیر در می‌آید.

$$\large E.J = - \frac{1}{\mu_{0}} \triangledown . (E \times B) - \frac{1}{\mu_{0}} B . \frac{\partial B}{\partial t} - \varepsilon_{0} E.\frac{\partial E}{\partial t}$$

$$\large \Rightarrow E . J = - \frac{ \partial }{ \partial t } ( \frac{ 1 }{ 2 } \varepsilon_{0} E^{2} + \frac{ 1 }{ 2 \mu_{0} } B^{2} ) - \frac{1}{\mu_{0}} \triangledown . (E \times B)$$
(20)

با استفاده از رابطه فوق و (9) داریم:

$$\large \frac{\text{d}W}{\text{d}t} = \int_{V}(- \frac{ \partial }{ \partial t } ( \frac{ 1 }{ 2 } \varepsilon_{0} E^{2} + \frac{ 1 }{ 2 \mu_{0} } B^{2} ) - \frac{1}{\mu_{0}} \triangledown . (E \times B))dV$$

$$\large \Rightarrow \frac{ \text{d}W }{ \text{d}t } = - \frac{ \partial }{ \partial t } \int_{V} ( \frac{ 1 }{ 2 } \varepsilon_{0} E^{2} + \frac{ 1 }{ 2 \mu_{0} } B^{2} ) dV - \frac{1}{\mu_{0}} \int_{V} \triangledown . (E \times B)dV$$
(21)

جهت ساده نویسی بیشتر با توجه به رابطه (3) و استفاده از قضیه دیورژانس ($$\begin{equation} \oint_{A} F \cdot d A = \int_{V}(\nabla \cdot F) d V \end{equation}$$) نتیجه می‌شود:

$$\large \frac{ \text{d}W }{ \text{d}t } = - \frac{ \partial U_{em} }{ \partial t } - \frac{1}{\mu_{0}} \oint_{A} (E \times B) . \widehat{n} dA$$
(22)

تعریف بردار پوئینتینگ

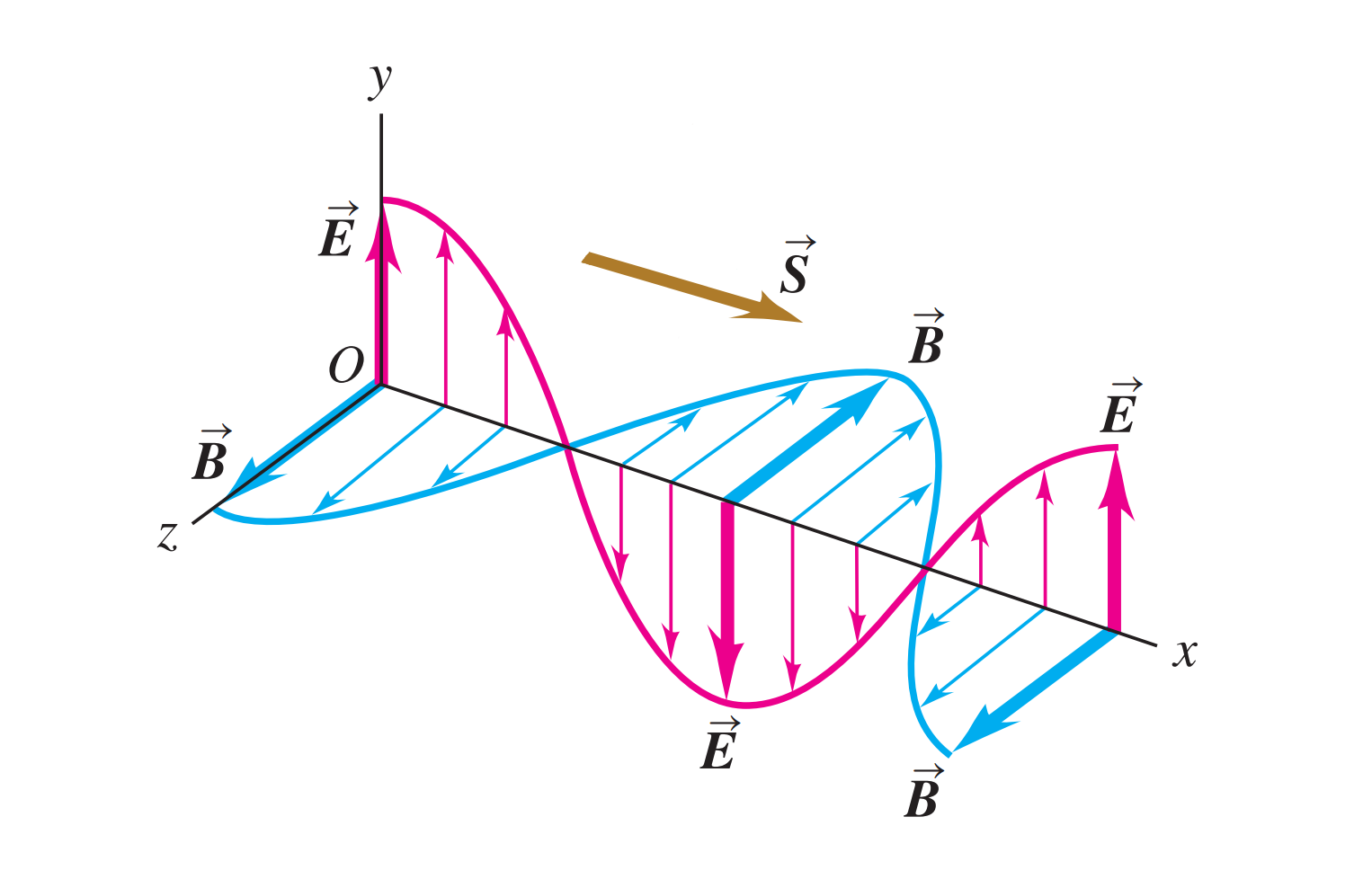
در مقاله «امواج الکترومغناطیسی — از صفر تا صد» با تعریف بردار پوئینتینگ (Poynting vector) آشنا شدید. بردار مذکور، بیانگر انرژی بر واحد زمان و سطح است که توسط میدان الکترومغناطیسی منتقل می‌شود. به عبارت دیگر، بردار پوئینتینگ، چگالی شار انرژی یا آهنگ انتقال انرژی بر واحد سطح (وات بر متر مربع) تعریف می‌شود.

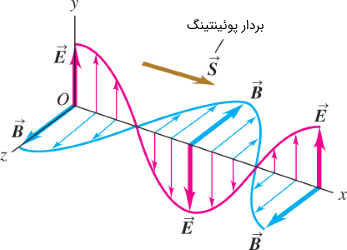
نکته قابل توجه در خصوص بردار پوئینتینگ این است که جهت آن، همان جهت انتشار موج الکترومغناطیسی است. بردار مذکور به صورت حاصل ضرب خارجی دوبردار $$E$$ و $$B$$ تعریف می‌شود. یعنی:

$$\large S = \frac{E \times B}{\mu_{0}}$$
(23)

با توجه به رابطه فوق، معادله (22) به صورت زیر خلاصه می‌شود:

$$\large \frac{ \text{d}W }{ \text{d}t } = - \frac{ \partial U_{em} }{ \partial t } - \frac{1}{\mu_{0}} \oint_{S} S . \widehat{n} dA$$
(24)

با توجه به دو رابطه (3) و (9) معادله فوق به شکل انتگرالی زیر در می‌آید:

$$\large \oint_{S} S . \widehat{n} d A + \int_{V} J . E d V = - \frac{ \partial }{ \partial t } \int_{V} ( u_{e} + u_{m} ) dV$$
(25)

رابطه فوق یا (24)، فرم انتگرالی قضیه پوئینتینگ بوده که بیان می‌کند تغییرات کار انجام شده روی توزیع بار توسط میدان الکترومغناطیسی (جمله سمت چپ تساوی رابطه ۲۴) برابر است با کاهش انرژی الکترومغناطیسی ذخیره شده در میدان (جمله اول سمت راست تساوی)، منهای انرژی شارش یافته از سطح S که حجم V را در بر می‌گیرد (جمله دوم سمت راست تساوی).

فرم دیفرانسیلی قضیه پوئینتینگ

در محاسبات مهندسی، فرم انتگرالی قضیه پوئینتینگ کاربردی نبوده و غالباً از فرم دیفرانسیلی آن استفاده می‌کنند. ‌می‌دانیم که کار انجام شده روی بارهای الکتریکی باعث افزایش انرژی مکانیکی آن‌ها می‌شود. در نتیجه چگالی انرژی مکانیکی $$u_{mech}$$ را به شکل زیر تعریف می‌کنیم:

$$\large \frac{\text{d}W}{\text{d}t} = \frac{\text{d}}{\text{d}t} \int_{V} u_{mech} dV$$
(26)

از رابطه (3)، چگالی انرژی الکترومغناطیسی به صورت زیر نتیجه می‌شود:

$$\large u_{em} = \frac{ 1 }{ 2 } \varepsilon_{0} E^{2} + \frac{ 1 }{ 2 \mu_{0}} B^{2}$$
(27)

با جایگذاری دو رابطه (26) و (27) در قضیه پوئینتینگ (معادله 24) و از استفاده از قضیه دیورژانس، انتگرال سطحی را به انتگرال حجمی تبدیل می‌کنیم. یعنی:

$$\large \frac{\text{d}}{\text{d}t} \int_{V} ( u_{mech} + u_{em} ) dV =\ - \int_{V} ( \triangledown . S ) dV$$
(28)

حال می‌توانیم عبارت‌های داخل دو انتگرال را مساوی یکدیگر قرار دهیم. در نتیجه:

$$\large \frac{\partial}{\partial t} ( u_{mech} + u_{em}) =\ - \triangledown . S$$
(29)

همان‌طور که ملاحظه می‌کنید، قضیه پوئینتینگ (معادله 24)، مشابه با معادله پیوستگی بار الکتریکی است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آنتن و فرستنده -- به زبان ساده
• امواج رادیویی -- به زبان ساده
• مخابرات فیبر نوری -- به زبان ساده

^^