فیلتر باترورث (Butterworth) — از صفر تا صد
در مطالب قبلی مجله فرادرس به فیلترهای مرتبه اول ساده مانند فیلترهای بالا گذر و پایین گذر پرداختیم که فقط از یک مقاومت تکی و یک المان راکتیو (خازن) در طراحی مدار فیلتر RC آنها استفاده شده بود. در این مطلب قصد داریم به بررسی یک نوع دیگر از فیلترها بپردازیم که «فیلتر باترورث» (Butterworth Filter) نام دارد.
فیلتر
در کاربردهایی مانند مخابرات و یا سیستمهای کنترل که از یک فیلتر به منظور شکلدهی طیف فرکانسی یک سیگنال استفاده میشود، شکل و یا عرض «باند گذار» (Transition Band) برای یک فیلتر مرتبه اول ساده ممکن است بسیار طولانی و عریض باشد و به همین دلیل لازم است از فیلترهای اکتیو با مرتبه بزرگتر از یک استفاده کنیم. به این نوع از فیلترها عموما فیلترهای مرتبه بالا و یا فیلترهای مرتبه n میگویند.
مرتبه فیلترها
پیچیدگی یا نوع فیلتر بر اساس درجه فیلتر تعریف میشود. درجه فیلتر نیز خود به تعداد المانهای راکتیو مانند خازن و یا سلف در طراحی مدار بستگی دارد. همچنین میدانیم که سرعت پاسخ فیلتر در ناحیه گذار و در نتیجه عرض باند گذار به درجه فیلتر بستگی دارند. برای یک فیلتر درجه اول استاندارد، شیب پاسخ گذار برابر با $$ 20 \; \text { dB/decade } $$ یا $$ 6 \; \text { dB/octave } $$ است. بنابراین برای یک فیلتر از درجه n، شیب پاسخ گذار برابر با $$ 20 n \; \text { dB/decade } $$ یا $$ 6 n \; \text { dB/octave } $$ خواهد بود.
بنا بر آنچه که گفتیم، یک فیلتر مرتبه اول دارای شیب پاسخ گذار برابر با $$ 20 \; \text { dB/decade } $$، یک فیلتر مرتبه دوم دارای شیب پاسخ گذار برابر با $$ 40 \; \text { dB/decade } $$ و شیب پاسخ گذار برای یک فیلتر مرتبه چهار برابر با $$ 80 \; \text { dB/decade } $$ است. توجه کنید که فیلترهای مراتب بالاتر مانند فیلترهای مرتبه سه، چهار، پنج و ... معمولا با استفاده از اتصال آبشاری فیلترهای مرتبه اول و مرتبه دوم به وجود میآیند. به عنوان مثال، میتوان دو فیلتر مرتبه دو را با آرایش آبشاری به یکدیگر متصل کرد تا یک فیلتر مرتبه چهار به دست آید. اگرچه به لحاظ تئوری هیچ محدودیتی برای مرتبه فیلترهایی که به این طریق ساخته میشوند وجود ندارد، اما هرچه مرتبه فیلتر بالاتر برود، اندازه فیلتر و نیز هزینه ساخت آن افزایش مییابد و از طرف دیگر دقت آن کاهش مییابد.
دههها و اکتاوها (Decades and Octaves)
در مقیاس فرکانسی، یک دهه برابر با افزایشی به اندازه ده برابر (ضرب در ۱۰) و یا کاهشی به اندازه ده برابر (تقسیم بر ۱۰) در نظر گرفته میشود. به عنوان مثال، تغییر از ۲ به ۲۰ هرتز، نشان دهنده یک دهه و تغییر از ۵۰ به ۵۰۰۰ هرتز، نشان دهنده دو دهه افزایش (از ۵۰ به ۵۰۰ یک دهه و از ۵۰۰ به ۵۰۰۰ یه دهه دیگر) است. اما یک اکتاو را دو برابر شدن (ضرب در ۲ شدن) و یا نصف شدن (تقسیم بر ۲ شدن) مقیاس فرکانسی در نظر میگیرند. به عنوان مثال، تغییر فرکانس از ۱۰ به ۲۰ هرتز نشان دهنده یک اکتاو و تغییر از ۲ به ۱۶ هرتز نشان دهنده نشان دهنده ۳ اکتاو (از ۲ به ۴ و سپس از ۴ به ۸ و در نهایت از ۸ به ۱۶) است که در هر گام فرکانس دو برابر میشود.
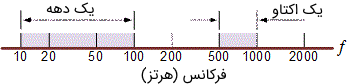
با در نظر گرفتن هر کدام از این مقادیر (دهه یا اکتاو)، مقیاس لگاریتمی در حوزه فرکانس و برای نمایش دادن مقادیر فرکانس هنگام کار کردن با تقویت کنندهها و فیلترها بسیار پرکاربرد است. بنابراین آگاهی از آنها بسیار ضروری است. در تصویر زیر نمایی از مقیاس فرکانسی لگاریتمی نشان داده شده است.
به این دلیل که مقاومتها و همچنین خازنهای تعیین کننده فرکانس دارای مقادیر برابر با یکدیگر هستند، در نتیجه فرکانس قطع یا فرکانس گوشه $$ f _ C $$ برای یک فیلتر مرتبه اول یا دوم و یا حتی سوم و چهارم نیز باید با هم یکسان هستند و با استفاده از فرمول آشنای زیر محاسبه میشوند:
$$ f _ C = \frac { 1 } { 2 \pi R C } $$
همانند آنچه که در فیلترهای مرتبه اول و دوم دیدم، میتوانیم فیلترهای مرتبه سه و چهار بالا گذر را نیز به وجود بیاوریم و برای این کار فقط لازم است به سادگی موقعیت المانهای تعیین کننده فرکانس (مقاومت و خازن) را در فیلتر پایین گذر معادل عوض کنیم. فیلترهای مرتبه بالاتر را نیز میتوان با استفاده از فرایندی طراحی کرد که در مطالب فیلترهای پایین گذر و بالا گذر به صورت مفصل بیان شد. با این حال، بهره کلی فیلترهای مرتبه بالا ثابت است؛ زیرا تمام المانهای تعیین کننده فرکانس ثابت هستند.
تخمین فیلتر
تا کنون مدار فیلترهای بالا گذر و پایین گذر و پاسخ فرکانسی و فاز نهایی آنها را بررسی کردهایم. یک فیلتر ایدهآل دارای مشخصههای بهره باند عبور بیشینه، بیشینه تضعیف باند توقف و نیز شیب بسیار تند برای گذار از باند توقف به باند هدایت است و به همین دلیل واضح است که پاسخ شبکه بسیاری از مدارات در این شرایط صدق میکنند. در نتیجه تعدادی از توابع تقریب در فیلترهای آنالوگ خطی وجود دارند که از روشهای ریاضی بهره میبرند تا تابع انتقال مورد نیاز ما در طراحی فیلتر را به صورت بهتر و دقیقتر تخمین بزنند.
به این طراحی، فیلتر باترورث میگویند. این فیلتر را با نامهای دیگری مانند فیلتر «چبیشف» (Chebyshev)، «بسل» (Bessel) و یا فیلتر «بیضوی» (Elliptical) نیز میشناسند. از بین ۴ تابع تقریب فیلتر آنالوگ خطی بالا، فقط فیلتر باترورث و به صورت خاص فیلتر باترورث پایین گذر در این مطلب مورد بررسی قرار میگیرند؛ زیرا این نوع، متداولترین تابع مورد استفاده است.
فیلتر باترورث پایین گذر
پاسخ فرکانسی تابع تقریب فیلتر پایین گذر باترورث را معمولا پاسخ «بیشینه مسطح» (Maximally Flat) میگویند؛ زیرا باند عبور به گونهای طراحی شده است که پاسخ فرکانسی در آن به لحاظ ریاضی تا حد امکان از صفر هرتز (مقدار DC) تا فرکانس قطع 3- دسیبل مسطح باشد و ریپل در آن وجود نداشته باشد. در فرکانسهای فراتر از نقطه قطع، پاسخ با سرعت ۲۰ دسیبل بر دهه یا ۶ دسیبل بر اکتاو در باند توقف به سمت صفر افت میکند. این فیلتر دارای «فاکتور کیفیت» (Quality Factor) یا Q برابر با ۰٫۷۰۷ است.
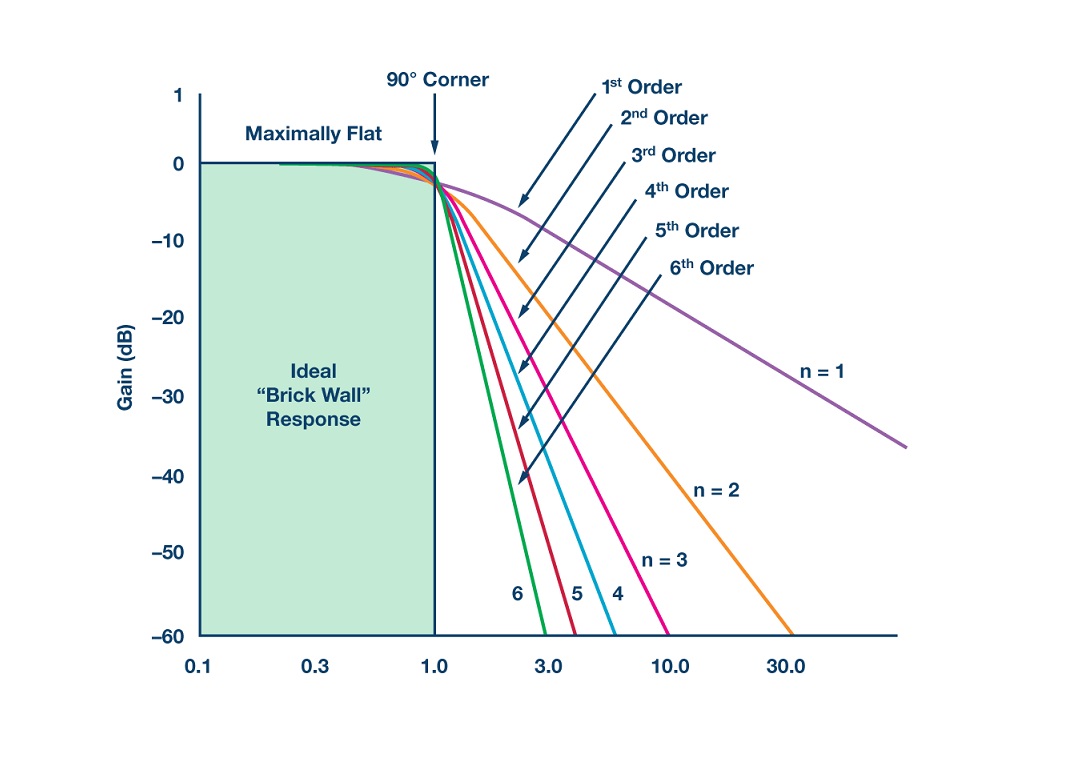
با این حال یکی از بزرگترین معایب فیلتر باترورث این است که فیلتر این پاسخ بسیار صاف در باند عبور را در عوض یک باند گذار عریض در هنگام تغییر از باند عبور به باند توقف به دست آورده است. همچنین فیلتر باترورث دارای مشخصه فاز بسیار ضعیفی است. پاسخ فرکانسی ایدهآل یک فیلتر که با نام «دیوار آجری» (Brick Wall) نیز شناخته میشود به همراه تقریب یک فیلتر باترورث استاندارد برای فیلترهای مراتب مختلف در تصویر زیر نشان داده شده است.

به این نکته توجه کنید که هر چه مرتبه فیلتر باترورث بالاتر باشد، تعداد طبقات آبشاری موجود در طراحی فیلتر نیز بیشتر میشود و پاسخ فرکانسی فیلتر به یک پاسخ ایدهآل یا دیوار آجری نزدیک تر میشود. البته در عمل، به دست آوردن یک فیلتر باترورث با پاسخ فرکانسی ایدهآل غیرممکن است؛ زیرا ریپلهای باند عبور بسیاری را تولید میکند. اگر یک معادله عمومی نشان دهنده یک فیلتر باترورث مرتبه n را در نظر بگیریم، آنگاه پاسخ فرکانسی به صورت زیر نوشته میشود:
$$ H ( j \omega ) = \frac { 1 } { \sqrt { 1 + \epsilon ^ 2 { ( \frac { \omega } { \omega _ p } ) } ^ { 2 n } } } $$
در رابطه فوق، n نشان دهنده مرتبه فیلتر، $$ \omega $$ برابر با $$ 2 \pi f $$ و $$ \epsilon $$ برابر با بیشینه بهره باند عبور ($$ A _ { max } $$) است. اگر $$ A _ { max } $$ در یک فرکانس برابر با فرکانس نقطه قطع یا گوشه 3- دسیبل یا $$ f _ C $$ تعریف شده باشد، آنگاه $$ \epsilon $$ برابر با یک میشود و $$ \epsilon ^ 2 $$ نیز برابر با یک خواهد بود. با این حال، اگر اکنون بخواهیم $$ A _ {max } $$ را در یک مقدار بهره ولتاژ متفاوت مثلا ۱ دسیبل تعریف کنیم، آنگاه مقدار جدید $$ \epsilon $$ به صورت زیر به دست میآید:
$$ H_ 1 = \frac { H _ 0 } { \sqrt { 1 + \epsilon ^ 2} } $$
در این رابطه، $$ H _ 0 $$ برابر با بهره باند عبور بیشینه یا $$ A _ { max } $$ و $$ H _ 1 $$ برابر با کمینه بهره باند عبور در نظر گرفته میشوند. حال معادله را برای به دست آوردن $$ \epsilon $$ ترانهاده میکنیم:
$$ \frac { H _ 0 } { H_ 1 } = 1.1220 = \sqrt { 1 + \epsilon ^ 2} \\
\epsilon = 0.5088 $$
پاسخ فرکانسی یک فیلتر را میتوان به صورت ریاضی با استفاده از تابع انتقال آن و با تابع انتقال ولتاژ استاندارد $$ H ( j \omega ) $$ به صورت زیر به دست آورد:
$$ H ( j \omega ) = \frac { V _ { out } (j \omega )} { V _ { in } (j \omega ) } $$
که در این رابطه، $$ V _ { out } $$ سیگنال ولتاژ خروجی، $$ V _ { in } $$ سیگنال ولتاژ ورودی، j برابر با جذر عدد 1- و $$ \omega $$ فرکانس برابر با $$ 2 \pi f $$ است. همچنین میدانیم که مقدار $$ j \omega $$ را میتوانیم با نماد S برای نمایش حوزه S نشان دهیم. بنابراین تابع انتقال نهایی برای یک فیلتر مرتبه دو پایین گذر به صورت زیر نوشته میشود:
$$ H ( S ) = \frac { V _ { out } (j \omega )} { V _ { in } (j \omega ) } = \frac { 1 } {S ^ 2 + S + 1} $$
چند جملهایهای نرمالیزه شده فیلتر باترورث پایین گذر
برای کمک به طراحی یک فیلتر باترورث پایین گذر، یک جدول از چندجملهایهای مرتبه دو پایین گذر نرمالیزه شده به صورت زیر وجود دارد که بر اساس آن میتوان مقادیر ضرایب متناظر با فرکانس گوشه یا قطع ۱ رادیان بر ثانیه را به دست آورد.
| چند جملهایهای مخرج نرمالیزه شده | مرتبه فیلتر (n) |
| $$ ( 1 + s ) $$ | 1 |
| $$ \left ( 1 + 1 . 4 1 4 s + s ^ { 2 } \right) $$ | 2 |
| $$ ( 1 + s ) \left ( 1 + s + s ^ { 2 } \right) $$ | 3 |
| $$ \left( 1 + 0 . 7 6 5 s + s ^ { 2 } \right)\left ( 1 + 1 . 8 4 8 s + s^ { 2 } \right) $$ | 4 |
| $$ ( 1 + s ) \left( 1 + 0 . 6 1 8 s + s ^ { 2 } \right) \left( 1 + 1 . 6 1 8 s + s ^ { 2 } \right ) $$ | 5 |
| $$ \left ( 1 + 0 . 5 1 8 s + s ^ { 2 } \right) \left ( 1 + 1 . 4 1 4 s + s ^ { 2 } \right) \left ( 1 + 1 . 9 3 2 s + s ^ { 2 } \right ) $$ | 6 |
| $$ ( 1 + s ) \left ( 1 + 0 . 4 4 5 s + s ^ { 2 } \right ) \left ( 1 + 1 . 2 4 7 s + s ^ { 2 } \right ) \left ( 1 + 1 . 8 0 2 s + s ^ { 2 }\right) $$ | 7 |
| $$ \left(1+0.390 s+s^{2}\right)\left(1+1.111 s+s^{2}\right)\left(1+1.663 s+s^{2}\right)\left(1+1.962 s+s^{2}\right) $$ | 8 |
| $$ ( 1 + s ) \left( 1 + 0 .3 4 7 s + s ^ { 2 } \right)\left ( 1 + s + s ^ { 2 } \right) \left ( 1 + 1 . 5 3 2 s + s ^ { 2 } \right) \left( 1 + 1 . 8 7 9 s + s ^ { 2 } \right) $$ | 9 |
| $$ \left( 1 + 0.313 s + s ^ { 2 } \right)\left( 1 + 0.908 s + s ^ { 2 } \right)\left( 1 + 1.414 s + s ^ { 2 } \right)\left( 1 + 1.782 s + s ^ { 2 } \right)\left( 1 + 1.975 s + s ^ { 2 } \right) $$ | 10 |
طراحی فیلتر باترورث پایین گذر
فرض کنید میخواهیم مرتبه یک فیلتر باترورث پایین گذر اکتیو را به دست آوریم که مشخصههای آن به صورت زیر هستند:
در فرکانس باند عبور یا $$ \omega _ p $$ برابر با ۲۰۰ رادیان بر ثانیه (۳۱٫۸ هرتز) مقدار بیشینه بهره باند عبور یا $$ A _ { max } $$ برابر با ۰٫۵ دسیبل است. همچنین مقدار $$ A _ { min } $$ برابر با 20- دسیبل در فرکانس باند عبور $$ \omega _ s $$ برابر با ۸۰۰ هرتز در نظر گرفته میشود. برای یک فیلتر باترورث با این مشخصهها طراحی مدار مناسب را نیز به دست آورید.
بهره باند عبور بیشینه این فیلتر $$ A _ { max } $$ برابر با ۰٫۵ دسیبل است، در نتیجه اندازه مطلق بهره برابر با ۱٫۰۵۹۳ به دست میآید. توجه کنید که در فرکانس ۲۰۰ رادیان بر ثانیه $$ 0.5\; dB = 20 * \log ( A ) $$ میباشد. با توجه به این محاسبات، مقدار $$ \epsilon $$ بر اساس رابطه زیر به دست میآید:
$$ 1.0593 = \sqrt { 1 + \epsilon ^ 2 } \\
\therefore \epsilon = 0.3495 \; and \; \epsilon ^ 2 = 0.1221 $$
همچنین میدانیم که کمینه بهره باند توقف $$ A _ { min } $$ برابر با 20- دسیبل است که با بهره ۱۰ ($$ - 20 \; dB = 20 * \log ( A ) $$) در فرکانس باند توقف $$ \omega _ s = \; 800 \; rads/s \; or \; 127.3 \;Hz $$ برابر است. با جایگذاری این مقادیر در معادله عمومی پاسخ فرکانسی یک فیلتر باترورث به نتیجه زیر میرسیم:
$$ \large \begin {array} {c}
H ( j \omega ) = \frac { H _ { 0 } }{ \sqrt { 1 + \varepsilon ^ { 2 } \left ( \frac { \omega _ { S } } { \omega _ { p } }\right) ^ { 2 n } } } \\
\frac { 1 } { 1 0 } = \frac { 1 } { \sqrt { 1 + 0 .1 2 2 1\left ( \frac { 8 0 0 } { 2 0 0 } \right) ^ { 2 n} } } \\
( 1 0 ) ^ { 2 } = 1 + 0 . 1 2 2 1 \times 4 ^ { 2 n}
\end {array} $$
$$ \begin {aligned}
& \therefore 100 - 1 = 0 . 1 2 2 1 \times 4 ^ { 2 n }\\
& 4 ^ { 2 n } = \frac { 9 9 } { 0 . 1 2 21 }= 8 1 0 . 8 1 1 \\
& 4 ^ { n } = \sqrt { 8 1 0 . 8 1 1 }= 2 8 . 4 7 5 \\
&\therefore n = \frac { \log 2 8 . 4 7 5 } { \log 4 } = 2 . 4 2
\end {aligned} $$
به این دلیل که n همیشه باید یک عدد صحیح باشد، در نتیجه نزدیک ترین مقدار به عدد ۲٫۴۲ برابر با ۳ است. بنابراین به یک فیلتر باترورث از مرتبه ۳ نیاز داریم. برای پیادهسازی یک فیلتر باترورث مرتبه ۳، به یک طبقه فیلتر باترورث مرتبه دو نیاز داریم که به صورت آبشاری به یک فیلتر باترورث از مرتبه یک متصل شده باشد. حال با توجه به جدول ضرایب چندجملهای نرمالیزه شده فیلتر باترورث پایین گذر که در قسمت قبل با آن اشنا شدیم، ضرایب برای یک فیلتر از مرتبه ۳ به صورت زیر است:
$$ ( 1 + s ) \left ( 1 + s + s ^ { 2 } \right) $$
این فیلتر بهرهای برابر با $$ 3 - A = 1 $$ یا $$ A = 2 $$ را ایجاد میکنند. به این دلیل که $$ A = 1 + \frac { R _ f } { R _ 1 } $$ است، در نتیجه با انتخاب مقدار ۱ کیلو اهم برای مقاومت فیدبک $$ R _ f $$ و نیز مقاومت $$ R _ 1 $$ عبارت $$ ( 1 \; k Ω / 1 \; k Ω ) + 1 = 2 $$ کاملا درست خواهد بود.
میدانیم که فرکانس قطع گوشه یا فرکانس 3- دسیبل $$ \omega _ 0 $$ را میتوان با استفاده از فرمول $$ \frac { 1 } { C R } $$ به دست آورد، اما در اینجا باید فرکانس را از رابطه فرکانس باند عبور $$ \omega _ p $$ به دست بیاوریم. در نتیجه داریم:
$$ \begin {aligned}
& H ( j \omega ) = \frac { H _ { 0 } } { \sqrt { 1 + \varepsilon ^ { 2 } \left ( \frac { \omega _ { O } } { \omega _ { p } } \right ) ^ { 2 n } } } \\
& 3 d B = 1 . 4 1 4 \text { at } \omega = \omega _ { 0 } \\
& \frac { 1 } { 1 . 4 1 4} = \frac { 1 } { \sqrt { 1 + \varepsilon ^ { 2 } \left ( \frac { \omega _ { O } } { \omega _ { p } } \right ) ^ { 2 n } } }
\end {aligned} $$
$$ \begin {array} {c}
2 = 1 + \varepsilon ^ { 2 } \left ( \frac { \omega _ { O } }{ \omega _ { P } } \right ) ^ { 2 n } \\
\therefore 1 = \varepsilon \left ( \frac { \omega _ { O } } { \omega _ { P } } \right ) ^ { n } \\
\omega _ { O } ^ { n } = \frac { \omega _ { P } ^ { n } } { \varepsilon }
\end{array} $$
$$ \begin {array} {c}
\omega _ { O } ^ { 3 } = \frac { 2 0 0 ^ {3 } }{ 0 . 3 4 9 5 } \\
\omega _ { O } ^ { 3 } = 2 2 . 8 8 9 \times 1 0 ^ { 6 } \\
\therefore \omega _ { O } = 2 8 3 . 9 3 = 2 8 4 \; \mathrm { rads } / \mathrm { s }
\end {array} $$
بنابراین فرکانس قطع گوشه برابر با ۲۸۴ رادیان بر ثانیه یا ۴۵٫۲ هرتز به دست میآید. حال با استفاده از رابطه آشنا $$ \frac { 1 } { C R } $$ میتوانیم مقدار مقاومت و خازن را در مدار فیلتر باترورث مرتبه سوم خود به دست آوریم:
$$ \begin {array} {l}
284 \mathrm { rads } / \mathrm { s }= \frac { 1 } { C R } \text { use avalue of } R = 1 0 \mathrm { k } \Omega \\
\therefore \text { Capacitor } C = \frac { 1 } { 284 \times 1 0 , 0 0 0 } = 0 . 3 5 2 \mathrm { u F }
\end {array} $$
نزدیکترین مقدار به ۰٫۳۵۲ میکرو فاراد برابر با ۰٫۳۶ میکرو فاراد یا ۰٫۳۶۰ نانو فاراد است. در نهایت مدار فیلتر باترورث پایین گذر مرتبه سه با فرکانس قطع گوشه ۲۸۴ رادیان بر ثانیه و یا ۴۵٫۲ هرتز و بهره بیشینه باند عبور ۰٫۵ دسیبل و بهره باند توقف کمینه ۲۰ دسیبل به صورت زیر است.
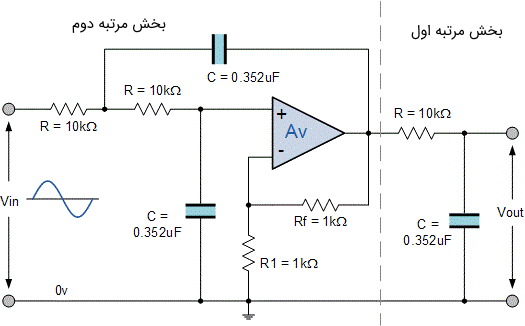
در این فیلتر باترورث پایین گذر مرتبه ۳ با فرکانس گوشه ۴۵٫۲ هرتز، مقدار خازن برابر با ۳۶۰ نانو فاراد و مقاومت آن ۱۰ کیلو اهم است.
اگر این مطلب برای شما مفید بوده است، مطالب و آموزشهای زیر نیز برای مطالعه بیشتر به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش الکترونیک ۳
- مجموعه آموزشهای مهندسی مخابرات
- آموزش طراحی فیلتر و سنتز مدار
- مبدل فرکانس به ولتاژ چیست و چگونه کار میکند؟ — از صفر تا صد
- پهنای باند معادل نویز (ENBW) چیست؟ — از صفر تا صد
- مدولاسیون کد پالس (PCM) چیست؟ — از صفر تا صد
^^











سلام خسته نباشید
ممنون از زحماتتون…همه اش عالی توضیح داده شد ولی کمی در بحث محاسبات پیچیدگی داشت و میشد روان تر شرح داد…
بنده نیاز به طراحی فیلتر باتروثی دارم با فرکانس ورودی ۵۰ هرتز و فرکانس قطع ۴۵۰ هرتز…لذا درخواست دارم در صورت امکان مناسب ترین مرتبه و اندازه المانهای مدار (مقدار اهم و فاراد) تعیین شود…خودم که نتونستم به کمک روش شما محاسبه کنم…با تشکر
واقعا ممنون.. سایتتون و هدفتون فوق العادست… هیچ منبعی نیست که انقدر تر و تمیز … با جزوه و فیلم انقدر خوب توضیح بده مطالب رو… واقعا ممنون.