فشار مطلق چیست؟ – به زبان ساده با مثال و تمرین

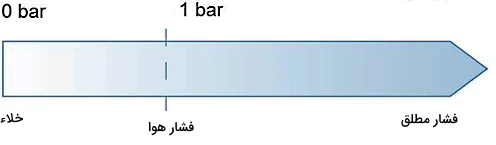
در شکل بالا مشاهده می‌کنید که فشار مطلق مقدار مثبتی دارد و مبدا آن، خلاء کامل با فشار صفر است. در حالی که مبدا فشار پیمانه‌ای فشار هوا است با مقدار ‎۱ bar. پیش از اینکه به توضیح بیشتر فشار مطلق بپردازیم، بهتر است ابتدا توضیح دهیم خود فشار به چه معنا است و چه فرمولی دارد.

کمیت فشار در فیزیک، به معنای اندازه نیروی عمودی است که به سطح یک جسم وارد می‌شود. بر این اساس فرمول اصلی فشار عبارت است از $P =\frac{F}{A}$ که در آن نیروی F بر حسب نیوتن (N) و مساحت A بر حسب متر مربع (m^۲) است. بنابراین واحد فشار در سیستم بین‌المللی یکاها یا SI برابر است با نیوتن بر متر مربع (N/m^۲) که پاسکال (Pa) نامیده می‌شود.

در تصویر، یک نیروی عمودی با دست به انتهای یک فنر وارد می‌شود. — فشار به معنای نیروی وارد بر واحد سطح است.

با اینکه معمولا در توصیف فشار از یک پیکان برای نشان دادن جهت وارد شدن آن استفاده می‌کنیم، اما فشار یک کمیت نرده‌ای یا عددی محسوب می‌شود، به این معنا که فقط دارای اندازه است و جهت ندارد. علت این مسئله این است که در فرمول فشار مولفه عمودی نیروی وارد بر سطح در نظر گرفته می‌شود. فشار انواع مختلفی دارد، مانند فشار پیمانه‌ای، فشار مطلق، فشار اتمسفریک و فشار دیفرانسیلی. یکی از مهم‌ترین انواع فشار که همیشه در کنار فشار مطلق قرار می‌گیرد، فشار پیمانه‌ای است و دانستن تفاوت این دو نوع فشار بسیار مهم است. در بخش‌‌های بعدی تفاوت‌های این دو فشار را کاملا توضیح خواهیم داد.

حدولی با سه خانه در زمینه سبز رنگ — فشار مطلق با مجموع فشار پیمانه‌ای و فشار هوا برابر است.

همچنین فشار در محیط‌های مختلف متفاوت است. برای مثال فشار در شاره‌ها فرمول دیگری دارد که به عمق شاره و چگالی آن وابسته است. انتظار داریم گازها هم به‌عنوان نوع دیگری از شاره‌ها، از قوانین فشار در مایعات پیروی کنند. اما در مورد نوعی خاصی از گازها، فشار با تغییرات دما و حجم تغییر می‌کند. به همین علت، بررسی فشار گازها کمی پیچیده‌تر است. در ادامه این مطلب ابتدا فشار در شاره‌ها را با تاکید بر فشار ناشی از وزن یک مایع توضیح می‌دهیم تا ببینیم فشار مطلق در شاره‌ها چگونه به‌دست می‌آید. سپس نحوه محاسبه فشار مطلق در یک گاز کامل را توضیح می‌دهیم.

فشار چیست ؟ – در فیزیک و به زبان ساده

فیلم آموزش فیزیک پایه دهم – فیزیک 1 در فرادرس

واحد فشار مطلق چیست؟

پس از اینکه تا حدی متوجه شدیم فشار مطلق چیست، در این بخش برخی از مهم‌ترین واحدهایی که برای بیان مقدار این نوع فشار بکار می‌روند را معرفی می‌کنیم. دو واحد مهم برای بیان مقدار فشار مطلق عبارت‌اند از:

پاسکال یا Pa
psi یا پوند بر اینچ مربع

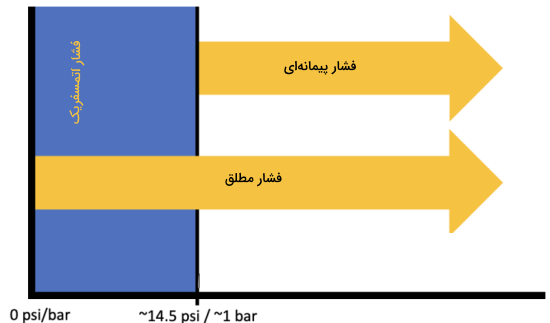
دو پیکان زرد افقی و دو یک ستون آبی — مقدار فشار اتمسفر و فشار در خلاء کامل بر حسب واحد psi

یکی از مرسوم‌ترین واحدهایی که برای بیان فشار مطلق استفاده می‌شود، واحد psi یا پوند بر اینچ مربع است. برای مثال طبق شکل بالا، در خلاء کامل اندازه فشار مطلق برابر است با ‎۰ psia (منظور از حرف a در انتهای psi این است که عدد بیان شده فشار مطلق است. اگر در انتهای psi حرف g نوشته شود، نشان‌دهنده این است که فشار پیمانه‌ای خوانده شده است). مشاهده می‌کنید که مقدار فشار مطلق در خلاء کامل و فشار اتمسفر هر دو بر حسب psi نشان داده شده‌اند و مقدار فشار اتمسفر بر حسب psi برابر است با ‎۱۴٫۵ psia که تقریبا با ‎۱ bar برابر است.

تبدیل واحد فشار – به زبان ساده

فیلم آموزش فیزیک – پایه دهم – مرور و حل تمرین در فرادرس

یادگیری فشار با فرادرس برای دانش‌آموزان

پیش از اینکه ببینیم تفاوت‌های فشار پیمانه‌ای با فشار مطلق چیست، در این بخش قصد داریم به معرفی چند فیلم آموزشی از مجموعه فرادرس برای دانش‌آموزان بپردازیم. همان‌طور که می‌دانید، در کتاب علوم تجربی پایه نهم، درسی با عنوان «فشار و آثار آن» و در کتاب فیزیک پایه دهم در مبحثی با عنوان «ویژگی‌های فیزیکی مواد» در مورد فشار صحبت شده است. بنابراین مشاهده فیلم‌های آموزشی مربوط به این کتاب‌های درسی به شما کمک می‌کند تا با دیدن تصاویر و شنیدن توضیحات بیشتر، درک بهتری نسبت به فشار به‌دست آورید:

تصور مجموعه آموزش‌های دروس پایه دهم — برای مشاهده مجموعه فیلم‌های آموزش دروس پایه دهم، روی تصویر کلیک کنید.

تفاوت فشار مطلق با فشار پیمانه‌ای چیست؟

قدم اول برای اینکه کاملا متوجه شویم فشار مطلق چیست، این است که تفاوت‌های آن را با فشار پیمانه‌ای بدانیم. اما پیش از آن، پیشنهاد می‌کنیم اگر دانش‌آموز هستید و تمایل دارید تمرین‌های بیشتری در مورد فشار حل کنید، به درس دوم از فیلم آموزشی فیزیک پایه دهم – مرور و حل تمرین فرادرس مراجعه کنید که لینک آن در ادامه برای شما قرار داده شده است:

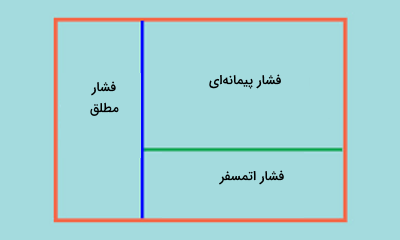
برخلاف فشار پیمانه‌ای که مرجع آن فشار اتمسفر است، مرجع اندازه‌گیری فشار مطلق خلاء کامل است. این مطلب در شکل زیر نشان داده شده است.

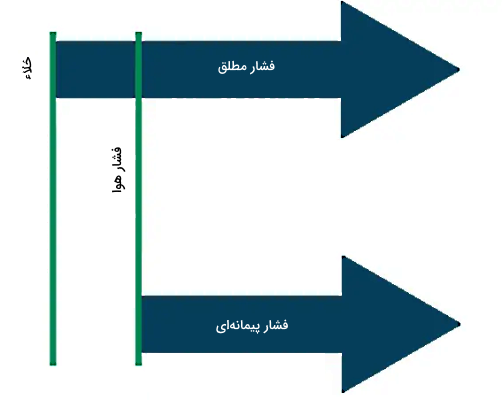
دو پیکان سورمه‌ای از خطوط سبز عمودی - فشار مطلق چیست؟ — تفاوت فشار مطلق و فشار پیمانه‌ای

همان‌طور که مشاهده می‌کنید، ابتدای پیکانی که بیان‌گر فشار مطلق است، در خلاء کامل قرار می‌گیرد، در حالی که فشار پیمانه‌ای از جایی شروع می‌شود که فشار اتمسفر قرار دارد. این شکل به این معنا است که مبدا اندازه‌گیری این دو نوع فشار با هم فرق دارد. فشار اتمسفر جز‌ئی از فشار مطلق است، اما برای فشار پیمانه‌ای در نظر گرفته نمی‌شود.

پس اگر در اندازه‌گیری فشار، اثر فشار هوا برای ما مهم باشد، باید فشار مطلق را محاسبه کنیم. در غیر این صورت، پیدا کردن فشار پیمانه‌ای کافی است. انتخاب مرجع فشار مطلق به این معنا است که صفر ما در خلاء کامل قرار دارد، در حالی که در مرجع فشار پیمانه‌ای، صفر ما در فشار اتمسفر است. بنابراین با اندازه‌گیری فشار پیمانه‌ای، فشار اتمسفر ‎۰ psig خوانده می‌شود در حالی که در مرجع فشار مطلق، خلاء کامل می‌شود ‎.۰ psia همچنین خلاء کامل در مرجع فشار پیمانه‌ای برابر می‌شود با ‎-۱۴٫۷ psig.

محاسبه فشار مطلق با فشار پیمانه‌ای منفی

نکته مهم دیگری که در مورد فشار پیمانه‌ای وجود دارد این است که این نوع فشار گاهی ممکن است مقدار منفی داشته باشد. پس باید ببینیم در چنین شرایطی فشار مطلق چیست. شکل مهم زیر را در نظر بگیرید. مقدار ثابت و مشخص فشار هوا در سمت چپ شکل نشان داده شده است. اگر فشار پیمانه‌ای مثبت اندازه‌گیری شود، در این صورت فشار مطلق برابر است با مجموع فشار پیمانه‌ای و فشار هوا. اگر به شکل دقت کنید، مجموع دو پیکان فشار پیمانه‌ای مثبت در سمت چپ تصویر و فشار هوا با پیکان فشار مطلق برابر خواهد شد.

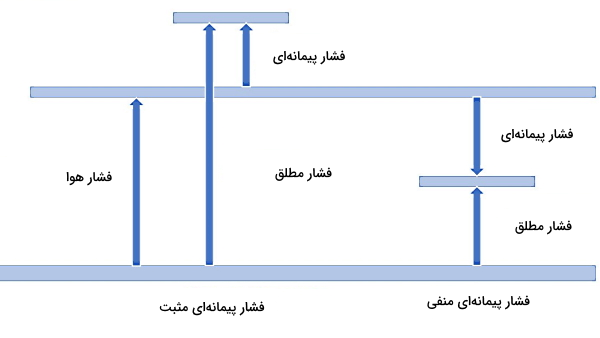
دیاگرامی شامل خطوx آبی افقی و عمودی و نوشته‌هایی در مورد انواع فشار — مقایسه فشار مطلق در دو نوع فشار پیمانه‌ای مثبت و منفی

نکته: منظورمان از مثبت بودن فشار پیمانه‌ای این است که بالاتر از خط افقی فشار اتمسفر قرار داشته باشد، چون همان‌طور که گفتیم این خط نشان‌دهنده مبدا اندازه‌گیری فشار پیمانه‌ای است. پس هر مقداری از فشار پیمانه‌ای زیر این خط، منفی در نظر گرفته می‌شود.

در سمت راست نمودار بالا، فشار پیمانه‌ای زیر خط افقی فشار هوا است، پس مقدار آن منفی است. در این شرایط باز هم فشار مطلق با مجموع فشار پیمانه‌ای و فشار هوا برابر است. اما چون عدد فشار پیمانه‌ای منفی است، پس در واقع این عدد از فشار هوا کم می‌شود تا فشار مطلق به‌دست آید. فشار پیمانه‌ای منفی را فشار خلاء هم می‌نامند. در بخش حل مثال و تمرین، با تفاوت این دو حالت بیشتر آشنا می‌شوید.

تفاوت فشار مطلق و نسبی — به زبان ساده

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

فرمول فشار مطلق چیست؟

در این بخش یاد می‌گیریم فرمول فشار مطلق چیست و با فرمول فشار پیمانه‌ای چه فرقی دارد. همان‌طور که گفتیم، تعریف فشار مطلق به این صورت است که با در نظر گرفتن خلاء کامل به‌عنوان مرجع، فشار اتمسفر و فشار پیمانه‌ای را شامل می‌شود. پس فرمول فشار مطلق می‌شود:

$P=P_0+P_g$

که در آن P₀ فشار اتمسفریک یا فشار هوا یا فشار جو، P_g فشار پیمانه‌ای یا فشار گیج و P فشار مطلق یا فشار کل است که در برخی متون با P_abs یا P_t هم نشان داده می‌شود. دقت کنید در این رابطه برای اینکه بتوانیم فشار جو را با فشار پیمانه‌ای جمع کنیم، لازم است واحد هر دو یکی باشد. در این صورت واحد فشار مطلق هم مانند واحد این دو نوع فشار است. از رابطه بالا می‌توانیم نتیجه بگیریم که فشار پیمانه‌ای با مرجع فشار اتمسفر، از محاسبه اختلاف فشار مطلق و فشار اتمسفر به‌دست می‌آید:

$\Rightarrow P_g=P-P_0$

صفر مطلق چیست ؟ – توضیح به زبان ساده

فیلم آموزش فیزیک 3 – حل تمرین در فرادرس

فشار اتمسفر چیست؟

همان‌طور که دیدید برای اینکه بدانیم مقدار فشار مطلق چیست، باید مقدار فشار پیمانه‌ای و فشار اتمسفر را داشته باشیم. در این قسمت راجع‌به فشار اتمسفر صحبت می‌کنیم. اتمسفر یا هوا در تمام ارتفاعات بالاتر از سطح دریا وجود دارد و دارای لایه‌‌های مختلفی است که با افزایش ارتفاع مشخص می‌شوند. در واقع با افزایش ارتفاع، فشاری که هوا اعمال می‌کند، کمتر خواهد شد.

فشار هوا در شرایط استاندارد، یعنی در سطح دریا، یک عدد ثابت است که دقیقا برابر با ‎۱۰۱۳۲۵ Pa و تقریبا به‌صورت ‎۱۰^۵ Pa در نظر گرفته می‌شود. معمولا فشار هوا با واحدی به نام اتمسفر (atm) نشان داده می‌شود. مقدار فشار هوا بر حسب اتمسفر برابر با عدد واحد است.

به‌ علاوه اگر با آزمایش توریچلی آشنا باشید، می‌دانید که توریچلی در این آزمایش از وسیله‌ای به نام بارومتر برای اندازه‌گیری فشار هوا استفاده کرد. در محاسبات او، فشار هوا با فشار ستونی از جیوه به ارتفاع ‎۷۶۰ mm برابر شد. از این آزمایش واحد دیگری برای بیان فشار ایجاد شد که میلی‌متر جیوه (mmHg) نام دارد و بر اساس نتیجه این آزمایش همواره داریم:

$1 \ atm = 10^5 \ Pa = 760 \ mmHg$

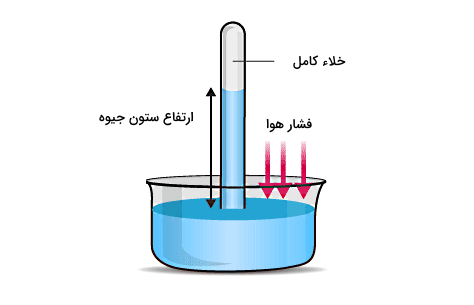
یک عدد لوله آزمایش داخل تشتی پر از مایع آبی رنگ برعکس شده است.

با توجه به شکل بالا، از برابری فشار هوای وارد بر سطح آزاد جیوه در داخل ظرف (P₀) با فشار ناشی از ستون جیوه در لوله آزمایش یا فرمول $P_g =\rho hg$ ، مقدار فشار هوا به‌دست می‌آید.

فشار اتمسفریک چیست؟ — به زبان ساده

حل مثال و تمرین از فرمول فشار مطلق

در این بخش با حل مثال‌های متنوع، می‌آموزید که روش استفاده از فرمول فشار مطلق چیست. همچنین در انتهای این بخش، چند سوال چهار گزینه‌ای برای شما قرار داده شده است که می‌توانید با پاسخ‌دهی به این تمرین‌ها، میزان یادگیری خود را بیازمایید.

مثال ۱

گیج فشار متصل به یک محفظه، فشاری به میزان ‎۴۰ kPa را نشان می‌دهد. اگر در آن مکان، فشار جو برابر با ‎۱۰۰ kPa باشد، کل فشار داخل محفظه چند پاسکال است؟

پاسخ

در این سوال فشار کل خواسته شده است که همان فشار مطلق است. پس از فرمول فشار مطلق استفاده می‌کنیم:

$P=P_g+P_0$

فشار هوا در سوال مشخص است. گیج متصل شده به محفظه، همان سنسور گیچ برای اندازه‌گیری فشار پیمانه‌ای است. پس مقدار فشار پیمانه‌ای یا P_g برابر است با ‎۴۰ kPa. بنابراین با قرار دادن اعداد داریم:

$\Rightarrow P=40 \ kPa+100 \ kPa=140 \ kPa$

اما در سوال مقدار فشار بر حسب پاسکال خواسته شده است. پس یک تبدیل واحد هم لازم است انجام دهیم. می‌دانیم پیشوند کیلو برابر است با ۱۰^۳. پس داریم:

$1 \ kPa=10^3 \ Pa \Rightarrow \frac{10^3 \ Pa}{1 \ kPa}=1$

$\Rightarrow 140 \ kPa=140 \ kPa \times\frac{10^3 \ Pa}{1 \ kPa}=140000 \ Pa$

مثال ۲

گیج خلاء متصل به یک محفظه، فشاری برابر با ‎۴۰ kPa را نشان می‌دهد. اگر فشار جو در آن نقطه ‎۱۰۰ kPa باشد، کل فشار داخل محفظه چند پاسکال است؟

پاسخ

فشار کل، همان فشار مطلق است. پس فرمول فشار مطلق را می‌نویسیم:

$P=P_g+P_0$

تفاوت مهم این سوال با سوال قبل در این است که گیج متصل شده به محفظه در این سوال، یک گیج خلاء است. بنابراین فشار پیمانه‌ای منفی خواهد بود. در واقع فشاری که داده شده است، فشار خلاء است که همان فشار پیمانه‌ای با علامت منفی است. پس مقدار فشار پیمانه‌ای یا P_g برابر است با ‎-۴۰ kPa. با قرار دادن اعداد در فرمول داریم:

$\Rightarrow P=-40 \ kPa+100 \ kPa=60 \ kPa$

در این سوال هم مقدار فشار بر حسب پاسکال خواسته شده است. پس با علم به اینکه پیشوند کیلو برابر است با ۱۰^۳، خواهیم داشت:

$1 \ kPa=10^3 \ Pa \Rightarrow \frac{10^3 \ Pa}{1 \ kPa}=1$

$\Rightarrow 60 \ kPa=60 \ kPa \times\frac{10^3 \ Pa}{1 \ kPa}=60000 \ Pa$

تصویر کارتنی از دانش‌آموز پسری که در حال انجام تکالیف خود است.

مثال ۳

اگر هوای داخل یک سیلندر فشار گیجی برابر با ‎‎۲۵۰ kPa داشته باشد، فشار مطلق چقدر است؟

پاسخ

مقار فشار پیمانه‌ای مشخص است. در مورد فشار هوا صحبتی نشده است، پس می‌توانیم مقدار آن را همان مقدار تقریبی ‎۱۰^۵ Pa در نظر بگیریم. برای جمع کردن این دو مقدار فشار، ابتدا واحدها را یکی می‌کنیم:

$1 \ kPa=10^3 \ Pa \Rightarrow \frac{10^3 \ Pa}{1 \ kPa}=1$

چون در صورت سوال مشخص نشده است بر حسب چه واحدی پاسخ دهیم، می‌توانیم جواب را بر حسب پاسکال یا کیلو پاسکال بنویسیم. انتخاب ما پاسکال است:

$P_g=250 \ kPa\times \frac{10^3 \ Pa}{1 \ kPa}=250000 \ Pa$

$P=P_g+P_0$

$\Rightarrow P=250000+100000=350000 \ Pa$

تمرین ۱

کدامیک از عبارت‌های زیر رابطه بین فشار مطلق، فشار پیمانه‌ای و فشار اتمسفر را به‌درستی نشان می‌دهد؟

$P_g=P-P_{atm}$

$P=P_g-P_{atm}$

$P_g=P+P_{atm}$

$P=P_{atm} -P_g$

پاسخ تشریحی

گزینه اول درست است. فرمول اصلی $P=P_g+P_{atm}$ است که با جابجایی به گزینه اول تبدیل می‌شود.

تمرین ۲

اگر فشار مطلق ‎‎۵۰ psi و فشار اتمسفریک ‎‎۳۷ psi باشند، فشار مطلق چقدر است؟

$13 \ psi$

$13 \ Pa$

$13 \ atm$

$13 \ mmHg$

پاسخ تشریحی

گزینه اول درست است. می‌دانیم طبق فرمول فشار مطلق داریم:

$P=P_g+P_0$

$\Rightarrow P_g=P-P_0$

$\Rightarrow P_g=50-37=13 \ psi$

فشار مطلق در شاره‌ها

آموختیم که فرمول فشار مطلق چیست و چگونه از فشار پیمانه‌ای به‌دست می‌آید. در شاره‌ها هم همین فرمول برقرار است، با این تفاوت که در شاره‌ها فشار پیمانه‌ای به شکل متفاوتی محاسبه می‌شود. در نتیجه فرمول فشار مطلق در شاره‌ها هم کمی متفاوت است. پس برای اینکه فشار مطلق در شاره‌ها را بررسی کنیم، اول باید ببینیم فشار پیمانه‌ای در چنین محیط‌هایی به چه صورت است.

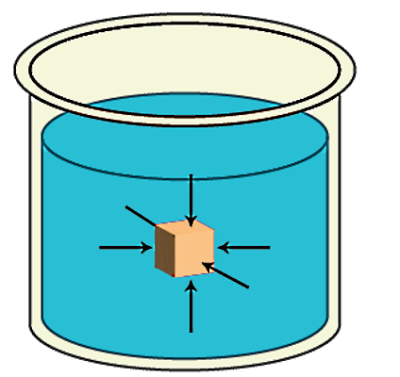
برای محاسبه فشار پیمانه‌ای در یک شاره، شکل بالا را در نطر بگیرید. فرض کنید مایعی با چگالی ρ، داخل یک ظرف استوانه‌ای ریخته شده است و در حالت سکون و بدون هیچ‌گونه حرکتی قرار دارد. با قرار دادن جسمی در عمق h از این مایع، می‌خواهیم ببینیم کل فشار یا فشار مطلق وارد شده به جسم از سوی مایع چقدر است. برای شروع از فرمول اصلی فشار استفاده می‌کنیم که در تمام محاسبات فشار صادق است:

$P =\frac{F}{A}$

طبق این فرمول، باید یک نیروی عمودی به جسم از طرف مایع وارد شود. این نیرو همان وزن سیالی است که در بالای جسم قرار دارد. یعنی به‌جای F، نیروی وزن یا W را قرار می‌دهیم:

$F=W=mg$

می‌دانیم چگالی یک ماده برابر است با جرم واحد حجم آن. پس با توجه به رابطه زیر، می‌توانیم جرم را بر حسب چگالی و حجم بنویسیم:

$\rho=\frac{m}{V}$

$\Rightarrow m=\rho V$

ستون شاره روی جسم با تقریب استوانه‌ای است با ارتفاع h و مساحت مقطع دایره‌ای A. پس با نوشتن فرمول حجم استوانه آخرین مرحله ساده‌سازی فرمول فشار انجام می‌شود:

$V=Ah$

$\Rightarrow m=\rho Ah$

$P =\frac{\rho Ahg}{A}=\rho hg$

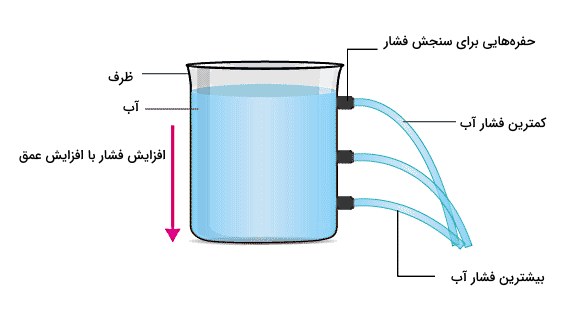
لیوان آبی دارای چند حفره است که از آنها آب خارج می‌‌شود. — رابطه فشار پیمانه‌ای در مایعات (Pg) با عمق (h)

$P_g =\rho hg$

بنابراین فشار پیمانه‌ای در شاره‌ها، همان فشار ناشی از نیروی وزن آن‌ها است که فقط به شتاب جاذبه، چگالی شاره و عمق یا ارتفاع سطح شاره از نقطه‌ای که مد نظر ما است، بستگی دارد. عواملی مثل شکل ظرف یا جرم شاره یا حجم آن روی این نوع فشار تاثیری ندارند.

با فرمول فشار پیمانه‌ای در شاره‌ها آشنا شدیم. مجددا شکل ابتدای این بخش را در نظر بگیرید تا ببینیم فشار مطلق وارد بر جسم چقدر می‌شود. طبق فرمول کلی که برای فشار مطلق داریم، مجموع فشار هوا و فشار پیمانه‌ای، فشار مطلق را به ما می‌دهد. پس اگر فشار پیمانه‌ای در مرحله قبل را با فشار هوا جمع کنیم، خواهیم داشت:

$P=P_g+P_0$

$P=\rho gh+P_0$

به این ترتیب فشار مطلق در شاره‌ها برابر است با فشار ناشی از وزن شاره به اضافه فشار هوای وارد بر سطح آزاد شاره. در بخش‌های قبل گفتیم که مقدار فشار هوا چقدر است. اگر این عدد را با فشار در مایعات جمع کنیم، خواهیم داشت:

$P=\rho gh+10^5 \ Pa$

نکته: فشار وارد بر تمام نقاطی که در عمق یکسانی داخل یک مایع قرار دارند، با هم برابر است. اگر به شکل زیر دقت کنید، در این لوله U شکل دو نقطه A و B هر دو داخل یک نوع مایع قرار دارند و هر دو عمق یکسانی نسبت به کف ظرف دارند. پس فشار در نقطه A با فشاری که به B اعمال می‌شود، برابر است.

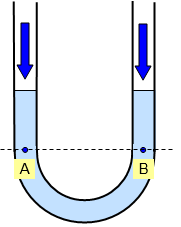
دقت کنید در این بررسی مایع حرکتی نداشت، پس سرعت شاره صفر است و فقط فشار استاتیکی آن محاسبه شده است. اگر مایع دارای سرعت v بود، با دینامیک سیالات مواجه بودیم و لازم بود فشار دینامیکی شاره هم محاسبه شود که موضوع این مطلب نیست. در ادامه با حل چند مثال و تمرین نحوه محاسبه فشار مطلق در مایعات را بیشتر یاد می‌گیریم. اگر علاقه‌مند هستید اطلاعات بیشتری در این زمینه داشته باشید، مطالعه مطلب «پیوستگی و بقای جرم در سیالات — از صفر تا صد» از مجله فردارس می‌تواند به شما کمک کند.

فشار در شاره ها – توضیح به زبان ساده

حل مثال و تمرین از فشار مطلق در شاره‌ها

در بخش قبل یاد گرفتیم که در شاره‌ها فرمول فشار مطلق چیست. حالا با حل چند سوال متنوع، چگونگی محاسبه این نوع فشار را با هم تمرین می‌کنیم.

مثال ۱

وقتی که یک دلفین در هوا می‌لغزد، فشار خارجی در حدود ‎۰٫۷۵ mHg حس می‌کند. اگر این دلفین ‎۵ m زیر سطح آب باشد، با در نظر گرفتن مقدار ‎۱۰۰۰ kg/m^۳ به‌عنوان چگالی آب و ‎۹٫۸ m/s^۲ برای شتاب جاذبه از سوی زمین، فشار مطلق وارد بر دلفین چقدر است؟

پاسخ

در قسمت اول سوال، فشار هوا با مقدار ‎۰٫۷۵ mHg داده شده است. بنابراین در این سوال باید از این عدد به‌جای فشار اتمسفر استفاده کنیم. برای به‌دست آوردن فشار مطلق، باید این عدد با فشار پیمانه‌ای جمع شود. فشار پیمانه‌ای وارد بر دلفین، فشار ناشی از نیروی وزن آبی است که با ارتفاع ‎۵ m روی بدن دلفین قرار می‌گیرد. پس لازم است از فرمول فشار در مایعات استفاده کنیم:

$P_g=\rho gh$

$\Rightarrow P_g=1000\times9.8\times5= 49050 \ Pa$

حالا می‌رویم سراغ فشار اتمسفر که بر حسب واحد دیگری داده شده است. چون این دو فشار با هم جمع می‌شوند، باید هر دو بر حسب یک واحد باشند. پس متر جیوه را به پاسکال تبدیل می‌کنیم. اما قبل از آن باید متر جیوه (mHg) به‌ شکل میلی‌متر جیوه (mmHg) نوشته شود:

$1 \ m=1000 \ mm \Rightarrow \frac{1000 \ mm}{1 \ m}=1$

$\Rightarrow 0.75 \ mHg= 0.75 \ mHg \times \frac{1000 \ mm}{1 \ m}=750 \ mmHg$

حالا طبق آنچه که گفتیم، می‌‌دانیم تبدیل واحد میلی‌متر جیوه (mmHg) به پاسکال (Pa) به شکل زیر است:

$760 \ mmHg= 10^5 \ Pa$

که می‌توانیم آن را به‌صورت زیر بنوسیم:

$\Rightarrow \frac{10^5 \ Pa}{760 \ mmHg}=1$

$\Rightarrow 750 \ mmHg= 750 \ mmHg \times \frac{10^5 \ Pa}{760 \ mmHg}=98684 \ Pa$

با جمع کردن دو فشاری که محاسبه شد، فشار کل یا فشار مطلق پیدا می‌شود:

$P=P_g+P_0$

$\Rightarrow P=49050 \ Pa+98684 \ Pa=147734 \ Pa$

مثال ۲

طبق شکل زیر، یک مانومتر را در نظر بگیرید که از مایعی با چگالی ρ_۱ تا ارتفاع h پر شده است. اگر مایع دیگری با چگالی ρ_۲ از بازوی سمت راست مانومتر داخل آن ریخته شود، طوری که بدون مخلوط شدن، روی مایع اول قرار بگیرد، نشان دهید از برابری فشار مطلق در دو نقطه، می‌توان نتیجه گرفت $\rho_1 h_1=\rho_2h_2$ .

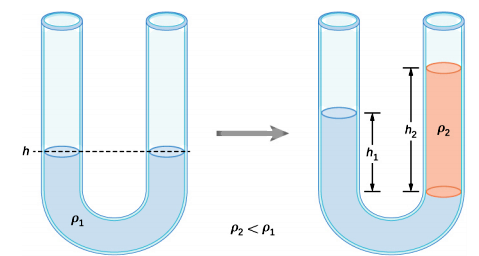
پاسخ

پس از اینکه مایع دوم روی مایع اول ریخته می‌شود، سطح مایع اول در بازوی راست لوله U شکل پایین می‌رود و در سمت مقابل، نسبت به حالت اول بالاتر قرار می‌گیرد. برای اینکه بتوانیم از اصل برابری فشار دو نقطه از یک مایع در عمق برابر استفاده کنیم، لازم است دو نقطه‌ای که انتخاب می‌کنیم کاملا داخل یک مایع قرار داشته باشند. برای مثال نقطه A را در بازوی راست در ابتدای ستون مایع با چگالی ρ_۲ در نظر می‌گیریم (نقطه A داخل مایع دوم نیست). حالا اگر نقطه B را در بازوی چپ و در همین سطح انتخاب کنیم، هر دو نقطه کاملا داخل مایع اول قرار دارند. به این ترتیب فشار وارد بر نقطه A یا P_۲ می‌شود مجموع فشار ناشی از ستون مایع با چگالی ρ_۲ و فشار اتمسفری که از دهانه باز لوله به سطح این مایع وارد می‌شود:

$P_2 =P_0+\rho_2gh_2$

اگر به رابطه بالا خوب دقت کنید، در واقع همان فرمول فشار مطلق برای نقطه A نوشته شده است که در آن $\rho_2gh_2$ برابر است با فشار پیمانه‌ای و P_۰ هم که فشار اتمسفر است. حالا می‌رویم سراغ فشار وارد بر نقطه B یا P_۱ که برابر است با مجموع فشار ناشی از وزن ستون مایع اول با ارتفاع h_۱ و فشار هوایی که از دهانه باز لوله به سطح این مایع اعمال می‌شود:

$P_1 =P_0+\rho_1gh_1$

این رابطه هم همان فرمول فشار مطلق وارد شده به نقطه B است. پس اصل برابری فشار در دو نقطه از یک مایع با عمق یکسان به‌ برابری فشار مطلق در این دو نقطه تبدیل شد. با برابر قرار دادن این دو فشار داریم:

$P_1 =P_2$

$\Rightarrow P_0+\rho_1gh_1 =P_0+\rho_2gh_2$

فشار اتمسفر در دو طرف این تساوی یکی است و حذف می‌شود. پس از ساده‌سازی داریم:

$\Rightarrow \rho_1h_1 =\rho_2h_2$

تمرین

فرض کنید فشار پیمانه‌ای شاره‌ای ۳ برابر فشار جو است. اگر عمق شاره دو برابر شود، فشار مطلق چند برابر خواهد شد؟

$\frac{7}{3}$

$2$

$\frac{13}{3}$

$3$

پاسخ تشریحی

گزینه اول صحیح است. در حالت اول با نوشتن فرمول فشار مطلق داریم:

$P_1=P_{g1}+P_0$

از طرفی طبق سوال فرض شده است که:

$P_{g1}=3P_0$

پس با جای‌گذاری این رابطه در فرمول اول، برای فشار مطلق در حالت اول و قبل از دو برابر شدن عمق شاره، داریم:

$\Rightarrow P_1=3P_0+P_0=4P_0$

حالا می‌رویم سراغ حالت دوم که در آن عمق شاره دو برابر شده است. طبق فرمول فشار در شاره‌ها برای فشار پیمانه‌ای خواهیم داشت:

$P_{g2}=2\rho gh$

در فرمول بالا اگر عمق h دو برابر شود، با فرض ثابت ماندن سایر کمیت‌ها، فشار پیمانه‌ای هم دو برابر خواهد شد:

$\Rightarrow P_{g2}=2P_{g1}$

پس در حالت دوم فشار پیما‌نه‌ای نسبت به حالت اول دو برابر خواهد شد. یعنی اگر در حالت اول فشار پیما‌نه‌ای سه برابر فشار هوا است، در این حالت فشار پیما‌نه‌ای شش برابر فشار هوا خواهد بود:

$\Rightarrow P_{g2}=2\times3P_0=6P_0$

در نهایت فشار مطلق در حالت دوم را به‌دست می‌آوریم و با نوشتن نسبت کسری فشار مطلق در دو حالت، تغییرات را بررسی می‌کنیم:

$P_2=P_{g2}+P_0$

$\Rightarrow P_2=6P_0+P_0=7P_0$

$\Rightarrow \frac{P_2}{P_1}=\frac{7}{3}$

فشار در مایعات — به زبان ساده

فشار مطلق در گازهای کامل

در ادامه مسیر یادگیری خود، می‌خواهیم ببینیم در مورد گازهای کامل فرمول فشار مطلق چیست. فشار مطلق در گازهای کامل با دو کمیت مهم دما و حجم گاز در ارتباط است. قوانین حاکم بر گازها که شامل سه قانون زیر است، رابطه این دو کمیت با فشار را به‌خوبی توصیف می‌کند:

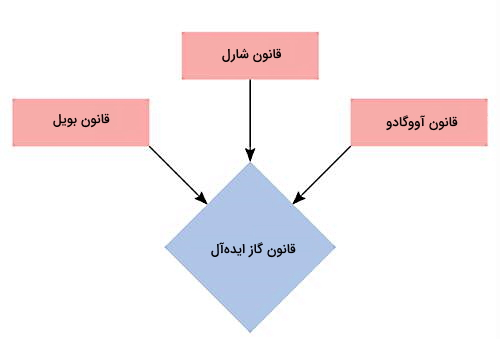
قانون بویل: اگر فشار مطلق وارد بر گازی کم شود، حجم آن زیاد می‌شود.
قانون شارل: اگر دمای گازی زیاد شود، حجم آن هم زیاد می‌شود.
قانون آووگادو: با افزایش مقدار یک گاز، حجم آن هم زیاد می‌شود.

قانون گازهای ایده‌آل یا قانون گازهای کامل، ترکیبی از این سه قانون است. پیش از پرداختن به این قانون مهم، بهتر است ابتدا گاز ایده‌آل (Ideal Gas) را تعریف کنیم.

گاز ایده‌آل یا گاز کامل چیست؟

در یک گاز ایده‌آل یا گاز کامل (Perfect Gas)، هیچ نیرویی بین ذرات تشکیل‌دهنده گاز وجود ندارد، بلکه ذرات به‌صورت کشسان با یکدیگر و با دیواره‌های ظرفی که در آن قرار دارند، برخورد می‌کنند. نقطه مقابل گاز کامل، گاز واقعی (Real Gas) است. در یک گاز واقعی، برخورد ذرات با هم کشسان نیست، چون بین ذارت تشکیل‌دهنده این گاز نیروهای جاذبه وجود دارد.

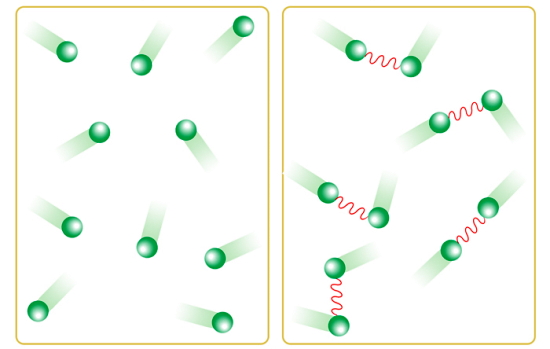
دو گروه ذرات سبز رنگ، در یک گروه ذرات با فنر قرمز به هم وصل شده‌اند. — برهم‌کنش ذرات در گاز واقعی (سمت راست) و گاز کامل (سمت چپ)

با توجه به این خصوصیات، حجم یک گاز واقعی از حجم گاز کامل بیشتر است، اما فشار آن نسبت به فشار گاز کامل کمتر است. در شکل بالا برهم‌کش‌ بین ذرات در یک گاز واقعی با موج سینوسی قرمز رنگی نشان داده شده است. تمام گازهای واقعی در شرایط فشار پایین و دمای نسبتا بالا تمایل دارند مانند یک گاز کامل رفتار کنند. در جدول زیر تفاوت‌های این دو نوع گاز بیان شده است:

گاز واقعی	گاز کامل
بین مولکول‌ها برهم‌کنش یا نیروی جاذبه داریم.	بین مولکول‌ها برهم‌کنش نداریم.
ذرات فضا اشغال می‌کنند.	ذرات فضا اشغال نمی‌کنند.
در برخوردها انرژی از بین می‌رود (برخوردها کشسان نیست).	برخوردها کشسان (الاستیک) است.

کمیتی که نشان می‌دهد گاز واقعی چقدر با گاز کامل متفاوت است، ضریب تراکم‌پذیری یا Z در گازها است. برای یک گاز کامل Z=۱، در حالی که برای گازهای واقعی Z≠۱.

گاز ایده‌ آل — به زبان ساده

قانون بویل (رابطه فشار مطلق با حجم)

در بخش قبل با مشخصات گاز کامل و گاز واقعی آشنا شدیم. گفتیم طبق قانون بویل (Boyle's Law)، فشار مطلق یک گاز کامل و حجم آن با هم رابطه معکوس دارند، یعنی هر چه فشار مطلق وارد به یک گاز کامل بیشتر شود، حجم آن کمتر می‌شود و برعکس. در این بخش بیشتر توضیح می‌دهیم که قانون بویل و ارتباط آن با فشار مطلق چیست.

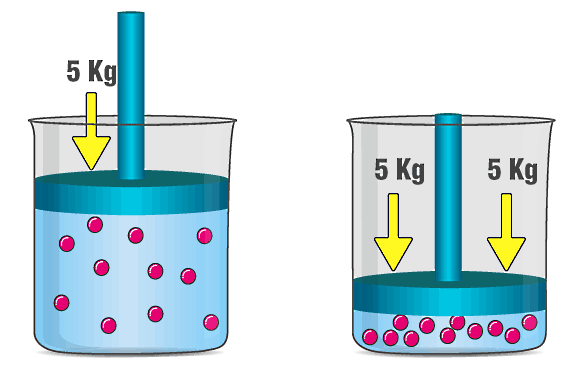
ذرات قرمز در دو ظرف شیشه‌ای نحن فشار پیستون — قانون بویل: کاهش حجم گاز کامل با افزایش فشار

در سمت چپ تصویر بالا پیستونی را مشاهده می‌کنید که نیرویی برابر با $F=W=mg=5\times10=50 \ N$ به گاز داخل محفظه وارد می‌کند. این نیرو باعث می‌شود فشاری به اندازه P_۱ به گاز وارد شود. در سمت راست تصویر، جرم پیستون دو برابر شده است، پس نیرویی به اندازه $F=W=mg=10\times10=100 \ N$ داریم که فشار P_۲ را ایجاد می‌کند. قطعا P_۲>P_۱ است. اما می‌بینید که حجم گاز کامل در حالت دوم از حجم در حالت اول کمتر شده است.

بنابراین موضوع قانون بویل، تغییرات حجم گاز کامل بر اثر فشار مطلق وارد بر آن است. طبق این قانون، رابطه بین فشار مطلق یک گاز کامل یا P و حجم آن (V) به‌ شکل زیر است:

$P \propto \frac{1}{V}$

علامت ∝ به معنای تناسب است. می‌توانیم رابطه بالا را به یک تساوی تبدیل کنیم:

$PV =x$

x یک عدد ثابت در نظر گرفته می‌شود. پس قانون بویل می‌شود:

$P_1V_1=P_2V_2=x$

یا

$P_1V_1=P_2V_2$

قانون بویل — به زبان ساده

قانون گاز کامل

در بخش قبل آموختیم ارتباط بین حجم یک گاز کامل و فشار مطلق چیست. در این بخش قانون بویل را تکمیل می‌کنیم و به قانون گاز کامل می‌رسیم. از ترکیب قانون بویل ( $P \propto \frac{1}{V}$ ) با قانون شارل ( $V \propto T$ ) و قانون آووگادو ( $V \propto n$ ) به قانون یا معادله گاز کامل می‌رسیم:

$PV = nRT$

P: فشار مطلق وارد بر گاز کامل بر حسب پاسکال (Pa)
V: حجم گاز کامل بر حسب متر مکعب (m^۳)
n: مقدار گاز کامل بر حسب مول (mol)
R: ثابت گازها
T: دمای گاز کامل بر حسب کلوین (K)

پس در قانون گازهای کامل، رابطه بین فشار مطلق وارد بر یک گاز ایده‌آل با کمیت‌هایی مثل حجم و دمای آن مشخص می‌شود.

$P = \frac{nRT}{V}$

قانون گازها — به زبان ساده

حل مثال و تمرین از فشار مطلق در گازهای کامل

در بخش قبل یاد گرفتیم که در مورد یک گاز کامل، وضعیت فشار مطلق چیست و با چه فرمولی محاسبه می‌شود. در این بخش با حل مثال‌های مختلف، نحوه استفاده از فرمول قانون گاز ایده‌آل برای پیدا کردن فشار مطلق را بهتر یاد می‌گیریم.

مثال ۱

اگر در دمای ‎۲۵ C مقدار ۰٫۰۲۶ مول گاز کلر، حجمی برابر با ‎۷۵۰ mL داشته باشد، فشار مطلق وارد بر این گاز چقدر است $(R = 8.31 \ \frac{J}{mol \ K})$ ؟

پاسخ

با داشتن حجم، دما و مقدار یک گاز، معادله گاز کامل می‌تواند در محاسبه فشار مطلق آن به ما کمک کند:

$PV = nRT$

$\Rightarrow P = \frac{nRT}{V}$

پیش از قرار دادن اعداد در این فرمول، لازم است تبدیل واحد برای کمیت‌های دما و حجم داشته باشیم. دما باید بر حسب کلوین و حجم بر حسب متر مکعب نوشته شود:

$T (K)=T(C)+273$

$\Rightarrow T (K)=25+273=298 \ K$

$1 \ mL= 10^{-3} \ L \Rightarrow 750 \ mL= 750\times10^{-3} \ L =0.75 \ L$

$1 \ m^3= 1000 \ L \Rightarrow 0.75 \ L= 0.75 \ L\times \frac{1 \ m^3}{1000 \ L}= 0.00075\ m^3$

$\Rightarrow P = \frac{0.026\times8.31\times298}{0.00075}=85847.8 \ Pa$

مثال ۲

در یک لوله بسته، مقادیر حجم و دمای هوا (با فرض اینکه هوا یک گاز کامل باشد) به‌ترتیب برابر هستند با ‎۲٫۸۷ m^۳ و ‎۳۰۰ K. اگر مانومتر متصل به دیواره لوله، فشار گیجی برابر با ‎۰٫۵ bar نشان دهد، با در نظر گرفتن ثابت گازها (R) با مقدار ‎۲۸۷ J/kgK برای هوا و فشار جو ‎۱ bar، جرم هوای داخل لوله به کیلوگرم چقدر است؟

پاسخ

در این سوال با توجه به داده‌های مسئله اگر قانون گاز کامل را بنویسیم، می‌توانیم جرم هوای داخل لوله را محاسبه کنیم:

$PV = nRT$

$\Rightarrow n = \frac{PV}{RT}$

گفتیم که n در این فرمول بر حسب مول بیان می‌شود و برابر با مقدار گاز است. اما در این سوال جرم بر حسب کیلوگرم خواسته شده است. از طرفی ثابت R هم بر حسب J/kgK داده شده است. پس می‌توانیم به‌جای n در فرمول بنویسیم m:

$\Rightarrow m= \frac{PV}{RT}$

اگر بخواهیم در رابطه بالا عددگذاری کنیم، فشار را نمی‌دانیم. پس ابتدا باید مقدار فشار مطلق را حساب کنیم:

$P=P_g+P_0$

$\Rightarrow P=0.5+1=1.5 \ bar$

مقدار فشار مطلق بر حسب بار به‌دست آمد. برای استفاده از P در فرمول قانون گازها، باید فشار مطلق بر حسب پاسکال نوشته شود. پس تبدیل واحد داریم:

$1 \ bar=10^5 \ Pa \Rightarrow \frac{10^5 \ Pa}{1 \ bar}=1$

$\Rightarrow 1.5 \ bar= 1.5 \ bar\times \frac{10^5 \ Pa}{1 \ bar}=150000 \ Pa$

$\Rightarrow m= \frac{PV}{RT}= \frac{150000\times2.87}{287\times300}=5 \ kg$

مثال ۳

تایر دوچرخه‌ای را در نظر بگیرید که با فشار مطلق ‎۷×۱۰^۵ Pa در دمای ‏‎۱۸ C کاملا پر از باد شده است. اگر دما تا ‎۳۵ C افزایش داده شود، با فرض ثابت بودن مقدار گاز و حجم آن، فشار مطلق چقدر می‌شود؟

پاسخ

در این مسئله دو حالت داریم. در حالت اول فرمول به‌صورت زیر است:

$P_1V = nRT_1$

$\Rightarrow P_1 =\frac{nRT_1}{V}$

$\Rightarrow \frac{P_1}{T_1} =\frac{nR}{V}$

دقت کنید مقدار و حجم گاز طبق فرض سوال ثابت می‌ماند. در حالت دوم داریم:

$P_2V = nRT_2$

$\Rightarrow P_2 =\frac{nRT_2}{V}$

$\Rightarrow \frac{P_2}{T_2} =\frac{nR}{V}$

$\Rightarrow \frac{P_1}{T_1} = \frac{P_2}{T_2}$

$\Rightarrow P_2= P_1\frac{T_2}{T_1}$

بنابراین در این رابطه عددگذاری می‌کنیم تا فشار مطلق در حالت دوم مشخص شود. ولی پیش از آن، دمای حالت اول و دوم را به کلوین تبدیل می‌کنیم:

$T (K)=T(C)+273$

$T_1 (K)=T_1(C)+273=18+273=291 \ K$

$T_2 (K)=T_2(C)+273=35+273=308 \ K$

$\Rightarrow P_2=7\times10^5\times\frac{308}{291}=7.4 \times10^5 \ Pa$

تمرین

اگر ‎۰٫۵ mol گاز نئون در دمای ‎۳۵ C داخل محفظه‌ای با حجم ‎ ۱۹ Lباشد، با در نظر گرفتن $R = 8.31 \ \frac{J}{mol \ K}$ ، فشار مطلقی که به این گاز وارد می‌شود، چند میلی‌متر جیوه است؟

$67354.7$

$511.8$

$500$

$67000$

پاسخ تشریحی

گزینه دوم درست است. برای محاسبه فشار وارد بر این گاز از فرمول قانون گازها استفاده می‌کنیم:

$PV = nRT$

$\Rightarrow P = \frac{nRT}{V}$

اما لازم است پیش از عددگذاری در فرمول، دما را به کلوین و حجم را به متر مکعب تبدیل کنیم تا فشار به پاسکال محاسبه شود. در انتها پاسکال را به میلی‌متر جیوه تبدیل خواهیم کرد:

$T (K)=T(C)+273$

$\Rightarrow T (K)=35+273=308 \ K$

$1 \ m^3= 1000 \ L \Rightarrow 19 \ L= 19 \ L\times \frac{1 \ m^3}{1000 \ L}= 0.019 \ m^3$

$\Rightarrow P = \frac{0.5\times8.31\times308}{0.019}=67354.7 \ Pa$

$760 \ mmHg=10^5 \ Pa \Rightarrow \frac{760 \ mmHg}{10^5 \ Pa}=1$

$\Rightarrow 67354.7 \ Pa= 67354.7 \ Pa\times \frac{760 \ mmHg}{10^5 \ Pa}=511.8 \ mmHg$

رفتار گازها — به زبان ساده

کاربرد فشار مطلق چیست؟

در این بخش می‌خواهیم بدانیم کاربرد فشار مطلق چیست. در واقع با توجه به اینکه شرایط جوی دارای افت و خیز است، در برخی موقعیت‌ها داشتن یک سیستم دقیق که از مرجع مناسبی برای اندازه‌گیری فشار نسبت به خلاء کامل استفاده می‌کند، ضروری است. برای مثال، مبدل‌های فشاری که با هدف پیش‌بینی آب و هوا استفاده می‌شوند، فشار مطلق محیط اطراف را اندازه‌ می‌گیرند.

پس یکی از مهم‌ترین کاربردهای فشار مطلق در پیش‌بینی‌های هواشناسی است. در این سیستم‌ها چنانچه به‌‌جای مبدل‌های فشار مطلق، مبدل‌های فشار پیمانه‌ای بکار روند، فشاری که خوانده می‌شود برابر است با ۰. همچنین مبدل‌های فشار مطلق در ساخت نیمه رساناها نیز کاربرد دارند، به‌ویژه در ذخیره‌سازی و تحویل مواد سمی مانند گازهای فسفین (PH_۳) و آرسین (AsH_۳).

سنسورهای فشار مطلق

در بخش‌های قبل یاد گرفتیم نحوه محاسبه فشار مطلق چیست. در ادامه بررسی کاربردهای این نوع فشار، در این بخش سنسورهای فشار مطلق را معرفی می‌کنیم. می‌دانیم فشار مطلق، صفر مطلق را به‌عنوان مرجع فشار استفاده می‌کند و نسبت به خلاء کامل اندازه‌گیری می‌شود. به همین علت، این نوع فشار علی‌رغم تغییرات محیطی یا تغییرات دما، دقیق باقی می‌ماند.

نوعی وسیله اندازه‌گیری — نمونه‌ای از یک سنسور فشار مطلق

معمولا از سنسور فشار مطلق در موقعیت‌هایی استفاده می‌شود که آزمایش موردنظر روی سیستمی با شرایط پایدار انجام می‌شود. برای مثال اگر بخواهید فشاری را اندازه‌گیری کنید که تحت تاثیر تغییرات دمایی قرار نمی‌گیرد، بهتر است سنسور فشار مطلق بکار ببرید. عموما چنین سنسوری شامل یک حفره مرجع سیل شده است که داخل آن خلاء کامل برقرار است تا تمام مولکول‌های هوایی که پشت دیافراگم حسگر قرار دارند، از حفره تخلیه شوند. واحد اندازه‌گیری فشار در سنسورهای فشار مطلق psia است. این نوع سنسورها در اندازه‌گیری‌های فشار بارومتریک، انجام تست نشتی در محفظه‌های غیرقابل انعطاف سیل شده، آنالیز گازها، ارتفاع‌سنج‌ها و بررسی عملکرد یک سری موتورها کاربرد دارند.

اندازه گیری فشار - از صفر تا صد

مقایسه کاربرد فشار مطلق با فشار پیمانه‌ای

اگر بخواهیم فشار مطلق و فشار گیج را از نظر کاربردی مقایسه کنیم، باید دقت کنیم که فشار پیمانه‌ای فشار اتمسفر را به‌عنوان مرجع خود استفاده می‌کند. بنابراین نسبت به فشار بارومتریک جاری اندازه‌گیری می‌شود. با توجه به اینکه فشار هوا با تغییرات آب و هوایی یا ارتفاع پیوسته در حال تغییر است، پس فشار گیج زمانی استفاده می‌شود که اندازه‌گیری ما نیازمند فرآیندی است که برای انجام عملکرد مورد نظر باید بر فشار اتمسفر غلبه کند.

وسیله‌ای برای سنجش شبیه ساعت که به چند لوله متصل است. — اندازه‌گیری فشار گیج در لوله‌ها

بر همین اساس سنسورهای فشار پیمانه‌ای برای اندازه‌گیری یا کنترل فشار در فرآیندهایی بکار می‌روند که آن فرآیند از تغییرات در فشار اتمسفریک تاثیر می‌پذیرد. برای مثال، اگر به دنبال اندازه‌گیری سطح مایع در یک مخزن با تهویه هستید، استفاده از سنسور گیج انتخاب خوبی است. اغلب سنسورهای فشار پیمانه‌ای دارای یک پروت فشار در بخش فرآیند هستند و فشار محیط از طریق یک دریچه به پشت حسگر اعمال می‌شود. یکی از ملموس‌ترین کاربردهای فشار پیمانه‌ای نسبت به فشار مطلق، اندازه‌گیری فشار خون است.

دقت کنید واحد اندازه‌گیری فشار برای این سنسورها psig است. اگر فشار مثبت باشد، آن را فشار گیج می‌دانیم. در غیر این صورت به فشاری که مقدار منفی داشته باشد یا مقدار آن در بازه فشار اتمسفر و خلاء کامل قرار بگیرد، فشار پیمانه‌ای خلاء یا فشار خلاء گفته می‌شود که با واحد psiv بیان می‌شود. همچنین ممکن است فشار در بازه خلاء کامل تا مقادیر مثبت فشار پیمانه‌ای قرار بگیرد که در این صورت فشار گیج ترکیبی نامیده می‌شود و واحد آن psic است. کابرد سنسورهای فشار پیمانه‌ای در اندازه‌گیری‌های فشار هیدرولیک، دندان‌پزشکی، اتوکلاو و مخازن باز است.

فشار استاتیک چیست؟ – توضیح به زبان ساده