شاره چیست؟ – به زبان ساده

در کنار رودخانه، به دور از هیاهوی شهر، نشسته‌اید و به جریان آب نگاه می‌کنید. جریان آبِ رودخانه ممکن است آرام یا متلاطم باشد. آشنایی با فیزیک سیالات یا شاره‌ها به شما این امکان را می‌دهد که نگاه متفاوت‌تری به جریان آب رودخانه داشته باشید. به هر ماده‌ای که بتواند جریان داشته باشد، شاره یا سیال گفته می‌شود. از دیدگاه تخصصی‌تر، شاره ماده‌ای است که تحت‌تاثیر نیروی برشی، به طور مداوم تغییر شکل می‌دهد. در این مطلب از مجله فرادرس، ابتدا به پرسش شاره چیست به زبان شاره پاسخ می‌دهیم، سپس با انواع شاره، مشخصات شاره‌ها مانند فشار، مقاومت شاره و ابرشاره‌ها آشنا خواهیم شد.

شاره چیست ؟

به هر ماده‌ای که بتواند جاری شود، شاره یا سیال گفته می‌شود. از دیدگاه تخصصی‌تر، شاره ماده‌ای است که تحت‌تاثیر نیروی برشی، به طور مداوم تغییر شکل می‌دهد. شاید از خود پرسیده باشید منظور از تغییر شکل به صورت مداوم چیست. برای درک بهتر این عبارت، چند مثال را با یکدیگر مرور می‌کنیم.

فرض کنید قطعه‌ای فلزی روی زمین قرار گرفته است. نیرویی برشی به صورت نشان داده شده در تصویر زیر بر بلوک فلزی وارد می‌کنیم. چه اتفاقی رخ می‌دهد؟ قطعه فلزی در راستای نیروی وارد شده، اندکی تغییر شکل می‌دهد. مقدار تغییر شکل این فلز را برابر $$\triangle x$$ در نظر می‌گیریم. پس از مدتی، تغییر شکل قطعه فلزی متوقف می‌شود. به بیان دیگر، بلوک فلزی به طور مداوم و پیوسته تغییر شکل نمی‌دهد.

در ادامه، فرض کنید به جای بلوک فلزی مقدار آب داریم. نیروی برشی مشابهی را در راستای افقی بر آب وارد می‌کنیم. سوالی که ممکن است مطرح شود آن است که آیا تغییر شکل آب مشابه تغییر شکل قطعه فلزی است یا خیر. پاسخ به این پرسش، خیر است. آب تا هنگامی که نیروی برشی وارد می‌شود، به طور پیوسته و مداوم تغییر شکل می‌دهد. از این‌رو، در تعریف شاره، عبارت تغییر شکل به صورت مداوم، بسیار حائز اهمیت است. این عبارت، تعریف شاره را از غیرشاره جدا می‌کند. سوال مهم دیگری که ممکن است مطرح شود آن است که چرا تغییر شکل بلوک فلزی پس از مقداری جابجا شدن، متوقف می‌شود. برای پاسخ به این پرسش باید بلوک فلزی را در مقیاس میکروسکوپی بررسی کنیم.

مولکول‌های تشکیل‌دهنده بلوک فلزی در فاصله بسیار نزدیک از یکدیگر قرار گرفته‌اند و توسط نیروی بسیار قوی یکدیگر را جذب می‌کنند. مقدار این نیرو به اندازه‌ای قوی است که می‌تواند بر نیروی برشی وارد شده بر فلز،‌ غلبه کند. در مقابل، اگر به مولکول‌های تشکیل‌دهنده آب در مقیاس مولکولی نگاه کنیم، نیروی جاذبه بین آن‌ها در بسیار ضعیف‌تر است. بنابراین، به حرکت درآوردن مولکول‌های آب به اطراف بسیار آسان‌تر خواهد بود. اگر دست خود را داخل آب حرکت دهید، مولکول‌های تشکیل‌دهنده آب به راحتی می‌توانند از روی دست شما عبور کنند، اما انجام این کار برای فلز غیرممکن است. چگونه‌ می‌توان شاره‌ها را براساس نوع نیروی بین‌مولکولی، طبقه‌بندی کرد؟ در ادامه مطلب به این پرسش پاسخ می‌دهیم.

مولکول‌های تشکیل‌دهنده آب به صورت پیوسته نسبت به یکدیگر حرکت می‌کنند و موقعیت آن‌ها نسبت به یکدیگر تغییر می‌کند. بنابراین، می‌توانیم بگوییم تمام مولکول‌های آب نسبت به یکدیگر به صورت نسبی حرکت می‌کنند. بنابراین، هنگامی‌که می‌گوییم شاره جریان دارد، منظورمان آن است که تمام مولکول‌های آن نسبت به یکدیگر در حرکت هستند. در نتیجه، شاره را به صورت دیگری نیز می‌توانیم تعریف کنیم، هر ماده‌ای که مولکول‌های تشکیل‌دهنده آن نسبت به یکدیگر می‌توانند آزادانه حرکت کنند. آیا می‌توانیم شکر یا آرد را به عنوان شاره در نظر بگیریم؟ خیر، مولکول‌های تشکیل‌دهنده شکر یا آرد نمی‌توانند آزادانه نسبت به یکدیگر با گذر زمان حرکت کنند. بنابراین، آن‌ها را نمی‌توانیم شاره در نظر بگیریم. توجه به این نکته مهم است که دانه‌های شکر و آرد نسبت به یکدیگر حرکت می‌کنند نه مولکول‌های آن‌ها.

همان‌طور که می‌دانیم ماده در حالت کلی به سه شکل جامد، مایع و گاز در طبیعت وجود دارد. مایعات و گازها را می‌توانیم به عنوان شاره در نظر بگیریم که می‌توانند جاری شوند. در ابتدای این بخش، شاره را در حالت کلی و کمی تخصصی‌تر تعریف کردیم. در ادامه این بخش، این مفهوم را به صورت تخصصی بررسی می‌کنیم.

تعریف شاره در مکانیک سیالات

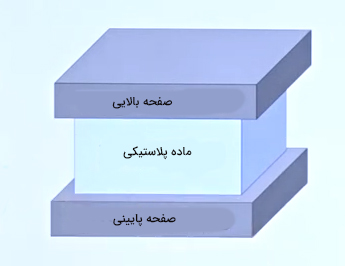
برای تعریف تخصصی شاره در مکانیک سیالات آزمایشی ساده را با یکدیگر انجام می‌دهیم. دو صفحه موازی را به صورت نشان داده شده در تصویر زیر در نظر بگیرید که ماده جامدی از جنس لاستیک مابین آن‌ها قرار گرفته است. همان‌طور که در تصویر مشاهده می‌کنید ماده پلاستیکی به گونه‌ای بین دو صفحه قرار گرفته است که فاصله آن از هر صفحه کمینه باشد و به راحتی نتواند نسبت به آن‌ها حرکت کند.

صفحه پایینی را ثابت و بدون حرکت، اما صفحه بالایی را متحرک در نظر می‌گیریم. تصویر بالا را از روبرو رسم می‌کنیم و صفحه متحرک بالا را با نیرویی برابر F می‌کشیم. چه اتفاقی رخ می‌دهد؟ با توجه به مقدار نیروی وارد شده بر صفحه بالایی، ماده پلاستیکی تغییر شکل می‌دهد. زاویه تغییر شکل نسبت به محور عمودی را برابر $$\beta$$ در نظر می‌گیریم. مقدار $$\beta$$ به مقدار نیروی F وابسته است. هرچه مقدار نیروی اعمال شده بیشتر باشد، زاویه $$\beta$$ نیز بزرگ‌تر خواهد بود.

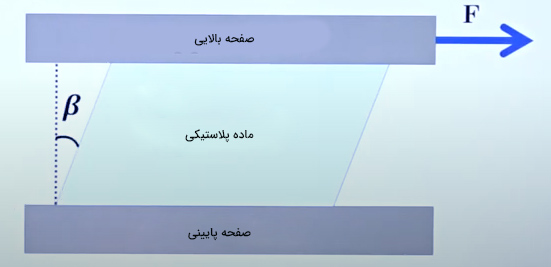
به این نکته توجه داشته باشید که تا هنگامی که نیروی F بر صفحه بالایی اعمال شود، زاویه $$\beta$$ با مقداری مشخص نیز وجود خواهد داشت. پس از حذف نیرو، ماده پلاستیکی به حالت اولیه خود بازمی‌گردد و زاویه $$\beta$$ برابر صفر می‌شود. این آزمایش را بار دیگر با ماده‌ای متفاوت انجام می‌دهیم و به جای ماده پلاستیکی بین دو صفحه، شاره‌ای مشخص مانند آب، قرار می‌دهیم. به طور مشابه، صفحه بالایی با نیرویی برابر F کشیده می‌شود. در این حالت، چه اتفاقی رخ می‌دهد؟ در آزمایش قبل، با اعمال نیرویی برابر F، زاویه $$\beta$$ ثابت باقی می‌ماند و تنها با افزایش یا کاهش نیرو، افزایش یا کاهش می‌یافت. اما در آزمایش دوم، این حالت صدق نمی‌کند. در این آزمایش، زاویه $$\beta$$ تا هنگامی‌که نیرو بر صفحه بالایی اعمال می‌شود، افزایش می‌یابد. تغییر شکل و افزایش زاویه $$\beta$$ پس از حذف نیرو متوقف می‌شود.

در آزمایش اول دیدیم که با افزایش نیروی F، مقدار $$\beta$$ نیز افزایش می‌یابد. اما در آزمایش دوم، با ثابت نگه داشتن نیروی F، زاویه $$\beta$$ به صورت پیوسته افزایش خواهد یافت. سوال مهمی که ممکن است مطرح شود آن است که در این آزمایش با افزایش مقدار F چه اتفاقی برای زاویه $$\beta$$ رخ می‌دهد. در این حالت، با افزایش مقدار F، نرخ تغییر حالت آب افزایش خواهد یافت. فرض کنید نرخ تغییر شکل یا نرخ تغییر زاویه $$beta$$ نسبت به زمان برابر $$\frac{\text{d}\beta}{\text{d}t}$$ است. به عنوان مثال، اگر نیروی اعمال شده برابر یک نیوتن و مقدار $$\frac{\text{d}\beta}{\text{d}t}$$ برابر ۴ درجه بر ثانیه باشد، پس از اعمال نیرو به اندازه ۳ ثانیه، تغییر شکل برابر ۱۲ درجه بر ثانیه خواهد بود.

با افزایش مقدار F، تغییر شکل همچنان با آهنگ بیشتری ادامه می‌یابد. این نکته را به یاد داشته باشید که در مواد جامد، تغییر شکل به صورت پیوسته و مداوم رخ نمی‌دهد. اگر مقدار نیروی اعمال شده در آزمایش دوم بسیار کوچک باشد، آهنگ تغییر شکل نیز بسیار کوچک خواهد بود. این بدان معنا است که گرچه مقدار نیروی اعمال شده بسیار کوچک است، تغییر شکل به صورت پیوسته، با آهنگ بسیار کوچک‌تری باز هم رخ می‌دهد. بنابراین، شاره ماده‌ای است که تحت‌تاثیر نیروی برشی، هر چقدر کوچک، به صورت پیوسته تغییر شکل می‌دهد. 

مهم ترین ویژگی های شاره چیست ؟

تا اینجا می‌دانیم شاره چیست و چگونه تعریف می‌شود. گرچه هر شاره از نظر ترکیب و ویژگی با شاره دیگر متفاوت است، ویژگی‌های مشترکی بین شاره‌های مختلف وجود دارند. ويژگی‌های کلی شاره را می‌توانیم به سه دسته کلی تقسیم کنیم:

• ویژگی‌های سینماتیک: با استفاده از این ویژگی‌ها می‌توانیم حرکت شاره را توصیف کنیم. سرعت و شتاب از جمله ویژگی‌های سینتماتیک شاره‌ها هستند.
• ویژگی‌های ترمودینامیکی: با استفاده از این ویژگی‌ها می‌توانیم حالت ترمودینامیکی شاره را توصیف کنیم. دما، چگالی و أنتالپی از جمله ویژگی‌های ترمودینامیکی شاره‌ها هستند.
• ویژگی‌های فیزیکی: با استفاده از این ویژگی‌ها، مانند رنگ و بو، می‌توانیم حالت فیزیک شاره را توصیف کنیم.

در بخش قبل فهمیدیم شاره چیست و در این بخش، با مهم‌ترین ویژگی‌های شاره آشنا می‌شویم. نخستین ویژگی شاره، چگالی یا چگالی جرمی آن است.

چگالی شاره چیست ؟

همان‌طور که در مطالب بالا اشاره شد، شاره می‌توانند مایع باشد یا گاز. در این قسمت می‌خواهیم بدانیم چگالی شاره چیست و چگونه می‌توان آن را اندازه گرفت. ابتدا چگالی را تعریف می‌کنیم. به مقدار ماده موجود در فضای مشخصی در سه‌بعد، چگالی گفته می‌شود. به این فضای مشخص در سه‌ بعد، حجم می‌گوییم. به طور معمول، واحد اندازه‌گیری حجم، مترمکعب، میلی‌لیتر یا سانتی‌متر مکعب است. بنابراین، چگالی را می‌توان به صورت مقدار جرم در حجم مشخصی از فضا تعریف کرد. در نتیجه، چگالی شاره در حالت کلی را می‌توان از رابطه زیر به‌دست آورد:

$$\rho = \frac { m } { V }$$

در ادامه، چگالی چند شاره را با یکدیگر به‌دست می‌آوریم.

محاسبه چگالی شربت پنکیک

برای اندازه‌گیری چگالی شربت پنکیک به وسایل زیر نیاز داریم:

• ظرف مدرج
• ترازو
• شربت پنکیک به مقدار لازم

ابتدا ظرف مدرج خالی را روی ترازو می‌گذاریم و جرم آن را اندازه می‌گیریم. جرم ظرف برابر ۳۹۳ گرم است. سپس، ظرف را با شربت پر می‌کنیم. حجم شربتی که داخل ظرف می‌ریزیم در حدود ۵۰ میلی‌لیتر است.

در ادامه، ظرف حاوی شربت را روی ترازو قرار می‌دهیم و جرم آن را دوباره اندازه می‌گیریم. جرم ظرف برابر ۴۵۶ گرم به‌دست می‌آید. برای محاسبه چگالی شربت، باید جرم آن را به‌دست آوریم. برای محاسبه جرم شربت، تنها کافی است جرم ظرف و شربت را از جرمِ ظرف، بدون شربت کم کنیم:

$$m_{syrup} = 456 - 393 = 63 \ g$$

بنابراین، جرم شربت برابر ۶۳ گرم و حجم آن برابر ۵۰ میلی‌لیتر است. برای به‌دست آوردن چگالی شربت، تنها کافی است جرم به‌دست آمده را بر حجم آن تقسیم کنیم:

$$\rho = \frac { 63  \ g } { 50 \ ml } \\ \rho = 1.26 \ \frac { g } { m l }$$

محاسبه چگالی آب

همانند حالت قبل، برای اندازه‌گیری چگالی آب به وسایل زیر نیاز داریم:

• ظرف مدرج
• ترازو
• آب به مقدار لازم

ابتدا ظرف مدرج خالی را روی ترازو می‌گذاریم و جرم آن را اندازه می‌گیریم. جرم ظرف برابر ۳۹۳ گرم است. سپس، ظرف را با آب پر می‌کنیم. حجم آبی که داخل ظرف می‌ریزیم در حدود ۵۰ میلی‌لیتر است. در ادامه، ظرف حاوی آب را روی ترازو قرار می‌دهیم و جرم آن را دوباره اندازه می‌گیریم. جرم ظرف برابر ۴۴۶ گرم به‌دست می‌آید.

برای محاسبه چگالی آب، باید جرم آن را به‌دست آوریم. برای محاسبه جرم آب، تنها کافی است جرم ظرف و آب را از جرمِ ظرفِ بدون آب کم کنیم:

$$m_{syrup} = 456 - 393 = 63 \ g$$

بنابراین، جرم شربت برابر ۵۳ گرم و حجم آن برابر ۵۰ میلی‌لیتر است. برای به‌دست آوردن چگالی شربت، تنها کافی است جرم به‌دست آمده را بر حجم آن تقسیم کنیم:

$$\rho = \frac { 53  \ g } { 50 \ ml } \\ \rho = 1.06 \ \frac { g } { m l }$$

همان‌طور که در مطالب بالا اشاره شد، مایعات و گازها را می‌توانیم به عنوان شاره یا سیال در نظر بگیریم. در بخش بعد، چگالی گاز را به دست می‌آوریم.

محاسبه چگالی گاز

چگالی برابر نسبت جرم به حجم اشغال شده توسط آن جرم است. محاسبه چگالی گاز مشابه محاسبه چگالی مایع یا جامد است. بنابراین، برای محاسبه چگالی گاز باید جرم و حجم آن را بدانیم. نکته‌ای که باید در مورد گازها بدانیم آن است که به جای حجم گاز، فشار و دمای آن داده می‌شود. بنابراین، باید حجم گاز را ابتدا حساب کنیم. برای یافتن چگالی گاز، گام‌های زیر را طی می‌کنیم:

• در بیشتر مواقع، به هنگام محاسبه چگالی گاز باید از فرمول‌های چگالی و قانون گاز ایده‌آل، همزمان استفاده کنیم.

$$\rho = \frac { m } { V } \enspace \\PV = nR T , \enspace V = \frac { n R T } { P } \\ \rho = m \times \frac { P } { n R T }\enspace ( M = \frac { m } { n } ) \\ \rho = \frac { P M } { R T }$$

M در رابطه فوق همان جرم مولی است.

• قانون گاز ایده‌آل تقریب بسیار خوبی از رفتار گازهای واقعی است.
• به یاد داشته باشید که به هنگام حل مسئله، دما برحسب کلوین نوشته شود.

مثال اول محاسبه چگالی گاز

چگالی گاز اکسیژن در فشار ۵ اتمسفر و دمای ۲۷ درجه سانتی‌گراد را به‌دست آورید.

پاسخ

در این مثال چگالی گاز را با داشتن نوع گاز،‌ فشار و دمای آن به‌دست می‌آوریم. فشار و دمای گاز داده شده است. برای محاسبه حجم گاز از قانون گاز ایده‌آل استفاده می‌کنیم:

$$V = \frac { n R T } { P }$$

در رابطه فوق، R ثابت جهانی گازها نام دارد و مقدار آن برابر $$0.0821 \ \frac { L. atm } { mol . K }$$ است. در رابطه بالا تمام کمیت‌ها، به جز n،‌ را برای محاسبه حجم گاز داریم. برای یافتن تعداد مول‌های گاز از رابطه $$n = \frac { m } { M }$$ استفاده می‌کنیم. در این رابطه، n تعداد مول‌های گاز، m جرم گاز و M جرم مولی گاز هستند. جرم مولی اکسیژن را می‌دانیم. رابطه تعداد مول‌ها، $$n = \frac { m } { M }$$،‌ زا در رابطه $$V = \frac { n R T } { P }$$ جایگزین می‌کنیم و به رابطه زیر می‌رسیم:

$$\frac { m } { V }  = \frac { M P } { R T } \\ \rho = \frac { P M } { R T }$$

گاز اکسیژن دو اتم اکسیژن دارد و جرم مولی آن برابر ۳۲ گرم بر مول است. دمای داده شده را باید برحسب کلوین بنویسیم. ۲۷ درجه سانتی‌گراد برابر ۳۰۰ کلوین است. در نتیجه، چگالی گاز اکسیژن برابر است با:

$$\rho = \frac { 32 \ \frac { g } { mol} \times 5 \ atm } { 0.0821 \ \frac { L . atm } { mol . K } \times 300 \ K }= 6.5 \ \frac { g } { L }$$

مثال دوم محاسبه چگالی گاز

چگالی گازی در دمای ۱۷ درجه سلسیوس و فشار ۷۶۰ تور برابر ۰/۱۶۹ گرم بر لیتر است. نوع گاز را مشخص کنید.

پاسخ

در این مثال، چگالی گاز، دما و فشار آن داده شده است. با توجه به این اطلاعات باید نوع گاز را مشخص کنیم. برای حل این مثال نیز باید از قانون گاز ایده‌آل استفاده کنیم:

$$PV = n R T$$

برای مشخص کردن نوع گاز باید جرم مولی آن را به‌دست آوریم. برای محاسبه جرم مولی، ابتدا تعداد مول‌های گاز، n، را با استفاده از رابطه قانون گاز ایده‌آل به‌دست می‌آوریم:

$$n = \frac { PV } {  R T}$$

مقدارهای داده شده را در رابطه فوق قرار می‌دهیم. فشار برحسب تور داده شده است. برای به‌دست آوردن تعداد مول باید فشار را برحسب اتمسفر بنویسیم. به این نکته توجه داشته باشید که ۷۶۰ تور برابر یک اتمسفر است. چگونه حجم را به‌دست می‌آوریم؟ برای محاسبه حجم از چگالی استفاده می‌کنیم. چگالی گار برابر ۰/۱۶۹ گرم بر لیتر است. برای به‌دست آوردن n می‌توانیم حجم را برابر یک لیتر و جرم گاز را برابر ۰/۱۶۹ گرم در نظر بگیریم. بنابراین، مقدار حجم در رابطه به‌دست آمده برای n را برابر یک لیتر قرار می‌دهیم. همچنین، مقدار ثابت جهانی گازها، R، برحسب لیتر و اتمسفر برابر $$0.0821 \ \frac { L . \ atm} { mol. \ k }$$ است. بنابراین، تعداد مول‌ها، n، به صورت زیر به‌دست می‌آید:

$$n = \frac { ( 1.00 \ atm ) \times ( 1.0 \ L ) } { ( 0.0821 \ \frac { L. atm } { mol . K } ) \times { 290 \ K }}= 0.042 \ mol$$

حجم را برابر یک لیتر در نظر گرفتیم، بنابراین جرم گاز را می‌توانیم برابر ۰/۱۶۹ گرم در نظر بگیریم. از این‌رو،‌ به راحتی می‌توانیم جرم مولی را به‌دست آوریم. جرم مولی برابر نسبت جرم ماده‌ در محفظه بر تعداد مول‌های آن است و به صورت زیر به‌دست می‌آید:

$$n = \frac { 0.169 \ g } { 0.042  \ mol } = 4.0 \ g$$

عدد به‌دست آمده بسیار کوچک و مربوط به گاز هلیوم است.

چگالی وزنی شاره چیست ؟

دومین ویژگی مهم شاره، چگالی وزنی نام دارد. این کمیت به صورت نسبت وزن شاره به حجم آن تعریف می‌شود. در بخش قبل،‌ چگالی یا چگالی جرمی را به صورت نسبت جرم به حجم شاره تعریف کردیم. اما در چگالی وزنی، به جای جرم از وزن استفاده می‌کنیم:

$$w = \frac { weight \enspace of \enspace fluid } { V }$$

واحد اندازه‌گیری چگالی وزنی شاره برابر نیوتن بر مترمکعب یا کیلونیوتن بر مترمکعب است. w را می‌توانیم به صورت زیر نیز بنویسیم:

$$w = \frac { W } { V } = \frac { m \times g } { V }$$

از آنجا که چگالی جرمی به صورت $$\rho = \frac { m } { V }$$ تعریف می‌شود، w را می‌توانیم برحسب چگالی جرمی به صورت زیر بنویسیم:

$$w = \rho \times g$$

به این نکته توجه داشته باشید که نام دیگر چگالی وزنی، وزن مخصوص است. در تمام کتاب‌ها و مطالب آموزشی، آب را به عنوان شاره‌ای استاندارد در نظر می‌گیرند. بنابراین، برای بیشتر مثال‌ها از آب به عنوان شاره استاندارد استفاده می‌کنیم. آیا می‌دانیم وزن مخصوص آب چه مقدار است؟ برای محاسبه وزن مخصوص آب از رابطه $$w = \rho \times g$$ استفاده می‌کنیم. چگالی آب و شتاب جاذبه زمین به ترتیب برابر ۱۰۰۰ کیلوگرم بر مترمکعب و ۹/۸۱ متر بر مجذور ثانیه است. در نتیجه، وزن مخصوص آب برابر است با:

$$w = \rho \times g = 1000 \times 9.81 = 9810  \ \frac { N } { m ^ 3 }$$

حجم مخصوص شاره چیست ؟

سومین ویژگی مهم شاره، حجم مخصوص نام دارد. این کمیت به صورت نسبت حجم شاره به جرم آن تعریف می‌شود:

$$v = \frac { V } { m }$$

یکای اندازه‌گیری حجمِ مخصوص برابر مترمکعب بر کیلوگرم است. به این نکته توجه داشته باشید که چگالی شاره برابر نسبت جرم به حجم شاره است. بنابراین، حجم مخصوص و چگالی معکوس یکدیگر هستند:

$$\rho = \frac { 1 } { v }$$

تا اینجا فهمیدیم چگالی، چگالی وزنی، وزن مخصوص و حجم مخصوص شاره چیست، در ادامه، با مفاهیمی مانند چگالی نسبی، دما، کشش سطحی و فشار آشنا می‌شویم.

چگالی نسبی شاره چیست ؟

چهارمین ویژگی مهم شاره، وزن مخصوص نام دارد. این کمیت به صورت نسبت چگالی شاره به چگالی آب تعریف می‌شود:

$$specific \enspace gravity (s ) =\frac { \rho _ { fluid } } { \rho_ { water } }$$

چگالی آب برابر ۱۰۰۰ کیلوگرم بر مترمکعب است. به عنوان مثال، چگالی شربت شکر برابر ۱۳۲۰ کیلوگرم بر مترمکعب است. وزن مخصوص آن به صورت زیر به‌دست می‌آید:

$$s_ { sugar \ syrup }= \frac {1320 } { 1000 } = 1.3$$

به طور مشابه، چگالی رب گوجه‌فرنگی برابر ۱۴۰۰ کیلوگرم بر مترمکعب و وزن مخصوص آن برابر ۱/۴ است. یکای اندازه‌گیری وزن مخصوص چیست؟ از آنجا که وزن مخصوص از نسبت دو چگالی به یکدیگر به‌دست می‌آید، بدون واحد است. سوال مهمی که ممکن است مطرح شود آن است که چرا این کمیت تعریف می‌شود؟ مواد مختلف پس از قرار گرفتن در آب، ممکن است:

• روی سطح آب بمانند.
• قسمتی از آن‌ها داخل آب فرو رود.
• به طور کامل در آب غرق شوند.

با استفاده از وزن مخصوص می‌توانیم بگوییم چه مقدار از ماده پس از قرار گرفتن در آب، داخل آن غوطه‌ور می‌شود. به عنوان مثال، وزن مخصوص آب برابر ۰/۲ است. این عدد بدان معنا است ۲۰ درصد از حجم چوب پس از قرار گرفتن در آب، داخل آن فرو می‌رود. اگر وزن مخصوص قطعه چوب، برابر ۰/۶ بود، ۶۰ درصد از آن زیر سطح آب قرار می‌گرفت.

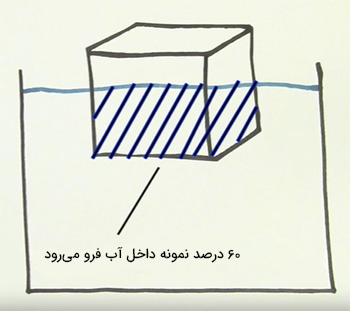
چگالی قطعه‌ای یخ در حدود ۹۲۰ کیلوگرم بر مترمکعب است. بنابراین، وزن مخصوص آن در حدود ۰/۹۲ به‌دست می‌آید. این عدد نشان می‌دهد که ۹۲ درصد حجم قطعه یخ، داخل آب فرو می‌رود. سوالی که ممکن است مطرح شود آن است که اگر چگالی جسمی از آب بیشتر باشد، چه اتفاقی رخ می‌دهد؟ قطعه‌ای مکعبی با چگالی ۲۷۰۰ کیلوگرم بر مترمکعب را در نظر بگیرید. در این حالت، وزن مخصوص، برابر ۲/۷ است. این بدان معنا است که ۲۷۰ درصد از حجم جسم در زیر آب قرار می‌گیرد. اما عددی بیشتر از ۱۰۰ درصد بی‌معنا است. بنابراین، اگر وزن مخصوص بیشتر از یک باشد، تمام جسم زیر آب قرار می‌گیرد. گاهی به جای تقسیم چگالی ماده بر چگالی آب، چگالی آن را نسبت به چگالی مایعی دیگر در نظر می‌گیریم.

به عنوان مثال، اگر داخل ظرفی به جای آب، روغن قرار داشته باشد، چگالی جسم را به چگالی روغن تقسیم می‌کنیم و وزن مخصوص آن را به‌دست می‌آوریم. به طور مشابه، برای شاره‌ها نیز، چگالی شاره را بر آب و گاهی بر شاره‌ای دیگر تقسیم می‌کنیم.

دمای شاره چیست ؟

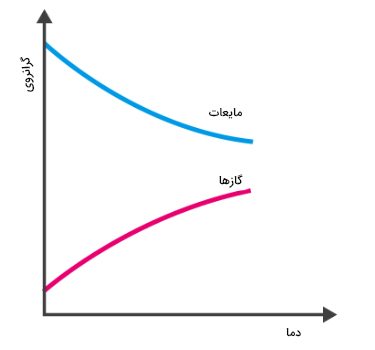
دما یکی از ویژگی‌های ترمودینامیکی شاره‌ها است و میزان گرمی یا سردی شاره را مشخص می‌کند. دما با یکی از واحدهای اندازه‌گیری سلسیوس، کلوین یا فارنهایت اندازه گرفته و گزارش می‌شود. از میان آن‌ها، کلوین یکی از رایج‌ترین واحدهای اندازه‌گیری دما در فیزیک است. مایعات و گازها با تغییر دما به صورت کاملا متفاوتی واکنش نشان می‌دهند. در نمودار زیر، تغییرات گرانروی گازها و مایعات نسبت به دما نشان داده شده است. گرانروی ویژگی دیگری از شاره‌ها است که در ادامه در مورد آن توضیح می‌دهیم. همان‌طور که در نمودار زیر دیده می‌شود، گرانروی مایعات با افزایش دما کاهش و گرانروی گازها با افزایش دما، افزایش می‌یابد.

کشش سطحی چیست ؟

تا اینجا می‌دانیم چگالی، حجم، وزن مخصوص و دمای شاره چیست. کشش سطحی ویژگی‌ مهم دیگر شاره‌ها، مایعات، است. به تمایل سطح مایع به کوچک شدن در سطح مقطع کمینه، کشش سطحی گفته می‌شود. علت ایجاد کشش سطحی، نیروهای جاذبه بین‌ مولکول‌های مایع است. به بیان دیگر، ذرات داخلی مایع، ذرات سطحی (ذرات قرار گرفته در مرز بین هوا و مایع) را برای رسیدن به سطح مقطع کمینه به سمت داخل می‌کشند. هرچه نیروهای بین‌مولکولی قوی‌تر باشد، کشش سطحی مایع نیز بزرگ‌تر خواهد بود.

آب، یکی از مایعاتی است که کشش سطحی بزرگی دارد. حشرات بسیاری با کمک کشش سطحی روی سطح آب می‌ایستند یا راه می‌روند. کشش سطحی آب در دمای ۱۰۰ درجه سلسیوس برابر $$0.059 \ \frac { N } { m }$$ و در دمای صفر درجه سلسیوس برابر $$0.079 \ \frac { N } { m}$$ است.

در مطالب بالا فهمیدیم برخی از ویژگی‌ها مهم شاره چیست. فشار یکی دیگر از مشخصه‌های مهم شاره، به خصوص مایعات، است که در ادامه در مورد آن صحبت می‌کنیم.

گرانروی شاره چیست ؟

بیشتر شاره‌ها (مایع یا گاز) در برابر حرکت از خود مقاومت نشان می‌دهند. به این مقاومت، گرانروی یا «ویسکوزیته» (Viscosity) می‌گوییم. گرانروی هنگامی به وجود می‌آید که حرکت نسبی بین لایه‌های شاره وجود داشته باشد. به بیان دقیق‌تر، گرانروی به اصطکاک داخلی بین لایه‌های شاره گفته می‌شود. اگر گرانروی شاره‌ای بزرگ باشد، این شاره در برابر حرکت مقاومت خواهد کرد، زیرا نیروهای بین مولکولی قوی منجر به ایجاد اصطکاک داخلی بسیار بزرگی می‌شوند. در نتیجه، این اصطکاک از حرکت آسان لایه‌های شاره نسبت به یکدیگر جلوگیری خواهد کرد. در مقابل، جریان شاره‌ای با گرانروی کوچک بسیار آسان است، زیرا نیروهای بین‌مولکولی در این شاره نسبت به نیروهای بین‌مولکولی در مایعی با گرانروی بزرگ، بسیار کوچک‌تر و در نتیجه، اصطکاک داخلی بین لایه‌های شاره کوچک و حرکت این لایه‌ها نسبت به یکدیگر آسان‌تر خواهد بود.

به این نکته توجه داشته باشید که گرانروی نه تنها در مایعات، بلکه در گازها نیز مشاهده می‌شود، اما در شرایط عادی تشخیص آن سخت خواهد بود. شاره‌ها براساس مقدار ویسکوزیته می‌توانند به انواع مختلفی تقسیم‌بندی شوند که در انتهای این بخش در مورد تقسیم‌بندی شاره‌ها به اختصار صحبت می‌کنیم.

تا اینجا می‌دانیم شاره چیست و چه ویژگی‌هایی دارد. از میان ویژگی‌های مختلف سیال مانند چگالی، فشار، گرانروی و غیره، فشار یکی از مهم‌ترین ویژگی‌های شاره است که در بخش بعد در مورد آن به صورت مفصل‌تری نسبت به ویژگی‌های دیگر توضیح می‌دهیم.

فشار شاره چیست ؟

در مطالب بالا با تعریف شاره آشنا شدیم. شاره‌ها شکل ظرفی را که در آن قرار دارند به خود می‌گیرند. به عنوان مثال، فرض کنید شیشه‌ای به شکل کره داریم. این شیشه کره‌ای را به طور کامل با آب پر می‌کنیم. هر سانتی‌متر یا متر مکعب این شیشه کره‌ای از آب پر شده است. در این حالت، آب، شکل ظرف کره‌ای را به خود می‌گیرد. حال فرض کنید ظرفی به شکل استوانه داریم و ان را با آب پر می‌کنیم. آب به چه شکلی درمی‌آید؟ استوانه، زیرا ظرف حاوی آب به شکل استوانه است. همچنین، به این نکته توجه داشته باشید که شاره‌ها مایع نیستند، بلکه گازها نیز شاره هستند. بنابراین، اگر ظرف‌های استوانه‌ای و کره‌ای را به جای آب، با گازی مانند اکسیژن پر می‌کردیم، این گاز باز هم شکل ظرفی که پر کرده است، را به خود می‌گرفت.

شاید از خود بپرسید گازی مانند اکسیژن و مایعی مانند آب چه تفاوتی با یکدیگر دارند. آب و اکسیژن چند تفاوت مهم با یکدیگر دارند، اما مهم‌ترین تفاوت آن ها آن است که مایع لزوما تمام ظرفی که در آن ریخته می‌شود را پر نمی‌کند، اما گاز تمام ظرف را پر می‌کند. به بیان دیگر، گازها تراکم‌پذیر، اما مایعات تراکم‌ناپذیر هستند. به عنوان مثال، اگر بطری پلاستیکی را با گاز پر کنیم، به راحتی می‌توانیم با فشردن بطری، حجم آن را تغییر دهیم. در واقع، با فشردن بطری گاز را متراکم می‌کنیم. اما این حالت برای بطری پر شده از آب صدق نمی‌کند و به راحتی نمی‌توانیم بطری پر شده از آب را فشرده و حجم آن را تغییر دهیم.

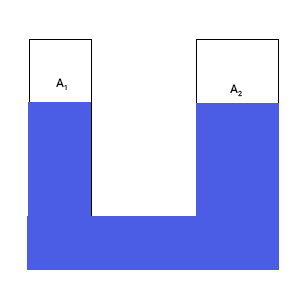
ظرفی U شکل به صورت نشان داده شده در تصویر زیر در نظر بگیرید. این ظرف از دو ستون استوانه‌ای تشکیل شده است که از پایین به یکدیگر وصل شده‌اند. قطر ستون سمت راست بزرگ‌تر از قطر ستون سمت چپ است. مساحت سطح ستون سمت چپ را برابر $$A_1$$ و مساحت سطح ستون سمت راست را برابر $$A_2$$ در نظر می‌گیریم. این ظرف را با مایعی مشخص، مانند آب یا جیوه، پر می‌کنیم. همان‌طور که اشاره شد یکی از مهم‌ترین ویژگی‌های مایع تراکم‌ناپذیر بودن آن است. در ادامه، در مورد نیرو و کار در شاره‌ها صحبت می‌کنیم.

کار چیست؟ کار به صورت حاصل‌ضرب نیرو در جابجایی تعریف می‌شود.

$$W = F . D$$

بر طبق تعریف مزیت مکانیکی، کار ورودی به سیستم برابر کار خروجی از آن است.

$$W_ { in } = W _ { out }$$

عبارت $$W_ { in } = W _ { out }$$ صورت دیگری از قانون پایستگی انرژی است. $$W_ { in }$$ مقدار انرژی است که به سیستم وارد و $$W_ { out}$$ مقدار انرژی است که از سیستم خارج می‌شود. رابطه $$W_ { in } = W _ { out }$$ را می‌توانیم به صورت زیر نیز بنویسیم:

$$F_ { in } . D _ { in } = F _ { out } . D _ { out }$$

فرض کنید نیرویی بر سطح $$A_1$$ وارد می‌شود. برای انجام این کار از پیستونی با مساحت $$A_1$$ استفاده می‌کنیم. مقدار نیروی وارد شده بر این پیستون برابر $$F_1$$ است. پیستون $$A_1$$ پس از وارد شدن نیروی $$F_ 1$$ بر آن به اندازه $$D_1$$ متر به سمت پایین جابجا می‌شود. چه مقدار آب جابجا می‌شود؟ یا به بیان دیگر، چه حجمی از آب جابجا می‌شود؟ مقدار آب جابجا شده برابر حجم استوانه نشان داده شده در تصویر زیر و برابر حاصل‌ضرب مساحت در ارتفاع است. همان‌طور که در تصویر مشاهده می‌کنید، مساحت برابر $$A_1$$ و ارتفاع برابر مقدار جابجایی آب، یعنی $$D_1$$، خواهد بود:

$$V_1 = A_1 \times D_1$$

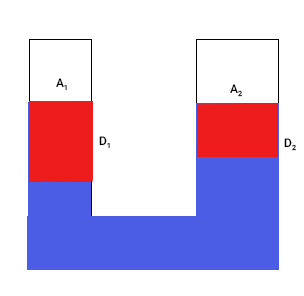
آب در ستون سمت چپ و پس از اعمال نیروی $$F_1$$ به سمت پایین حرکت می‌کند. مقدار آبِ جابجا شده باید جایی رفته باشد. همان‌طور که می‌دانیم مایعات تراکم‌ناپذیر هستند و نمی‌توانیم حجم کلی آن‌ها داخل ظرف را تغییر دهیم. بنابراین، با کاهش ارتفاع آب در ستون سمت چپ، ارتفاع آن در ستون سمت راست باید افزایش یابد. بنابراین، ارتفاع آب در ستون سمت راست به اندازه $$D_2$$ افزایش می‌یابد. به این نکته توجه داشته باشید که تغییر حجمِ آبِ جابجا شده در ستون سمت چپ باید با حجم آبِ جابجا شده در ستون سمت راست برابر باشد. حجم آبِ جابجا شده در ستون سمت راست برابر است با:

$$V_2 = A_1 \times D_1$$

حجم‌های $$V_1$$ و $$V_2$$ با یکدیگر برابر هستند:

$$V_1 = V_2 \\ A_1 D _ 1 = A_2 D_2$$

بار دیگر به رابطه $$F_ { in } . D _ { in } = F _ { out } . D _ { out }$$ برمی‌گردیم و نیروی ورودی و خروجی را برای راحتی کار با اندیس‌های یک و دو نشان می‌دهیم. در نتیجه، این رابطه به صورت زیر نوشته می‌شود:

$$F_ { 1 } . D _ { 1  } = F _ { 2 } . D _ { 2 }$$

سمت چپ رابطه بالا را به ترتیب در $$A_1$$ ضرب و بر $$A_1$$ تقسیم و به طور مشابه سمت راست رابطه فوق را نیز در $$A_2$$ ضرب و بر $$A_2$$ تقسیم می‌کنیم.

$$\frac { F _ 1 } { A _ 1 } . A_1 . D_1 = \frac { F _ 2 } { A _ 2 } . A_2 . D_2$$

آیا می‌دانیم عبارت $$\frac { F_ 1 } { A_ 1 }$$ چه چیزی را نشان می‌دهد؟ این عبارت کمیتی به نام فشار را تعریف می‌کند. فشار به صورت نسبت نیرو بر مساحتی که نیرو بر آن وارد می‌شود، تعریف می‌شود. همچنین، حاصل‌ضرب $$A_1 D_1$$ برابر حجم آبِ جابجا شده در ستون سمت چپ است. بنابراین، تساوی نوشته شده در بالا را می‌توانیم به صورت زیر بنویسیم:

$$P_1 .  V_ 1 = P_2 .  V_ 2$$

گفتیم حجم‌های $$V_ 1$$ و $$V_2$$ با یکدیگر برابر هستند. بنابراین، با حذف $$V_ 1$$ و $$V_2$$ از طرفین رابطه فوق، داریم:

$$V_ 1 = V_ 2$$

بر طبق رابطه به‌دست آمده، فشار ورودی به سیستم برابر فشار خروجی از سیستم است. به این نکته توجه داشته باشید که در تساوی به‌دست آمده از نیروی جاذبه زمین صرف‌نظر کردیم. در ادامه، این رابطه را با توجه به وجود نیروی جاذبه زمین اصلاح می‌کنیم. از رابطه به‌دست آمده نتیجه می‌گیریم هر فشار خارجی که به مایع تراکم‌ناپذیر وارد می‌شود، در سراسر مایع به صورت مساوی تقسیم می‌شود. به این حالت، اصل پاسکال گفته می‌شود. ظرفی پر شده از آب را به صورت نشان داده شده در تصویر زیر در نظر بگیرید که پیستونی در دهانه آن قرار دارد.

بر طبق اصل پاسکال، اگر فشاری به اندازه $$P_1$$ را به پیستون وارد کنیم، این فشار آب را کمی فشرده می‌کند. مایع،‌ در اینجا آب، تراکم ناپذیر است، بنابراین فشار وارد شده به پیستون، در سراسر مایع به صورت برابر و یکنواخت پخش می‌شود. ظرف U شکلی را به صورت نشان داده شده در تصویر زیر در نظر بگیرید. فشار وارد شده به سیستم برابر فشار خروجی از آن است.

$$P_ i = P _ o$$

فشار، برابر نیرو تقسیم بر مساحت سطحِ اعمال نیرو است. در نتیجه، رابطه $$P_ i = P _ o$$ به صورت زیر نوشته می‌شود:

$$\frac { F_ i } { A_ i } = \frac { F _ o } {A_ o }$$

فرض کنید فشار وارد شده به ستون سمت چپ در شکل بالا برابر ۱۰ پاسکال،‌ مساحت $$A_i$$ برابر ۲ مترمربع و مساحت $$A_o$$ برابر ۴ مترمربع است. مقدار نیروی خروجی چه مقدار است؟ برای به‌دست آوردن نیروی خروجی،‌ ابتدا نیروی ورودی را به‌دست می‌آوریم:

$$P_ i = \frac { F _ i } { A_ i } \\ 10 = \frac { F _ i } { 2 } \\ F _ i = 20 \ N$$

در ادامه، نیروی خروجی را با استفاده از رابطه $$\frac { F_ i } { A_ i } = \frac { F _ o } {A_ o }$$ به‌دست می‌آوریم:

$$\frac { 20 } { 2 } = \frac { F _ o } {4 } \\ F_ o = 40 \ N$$

فشار در عمق شاره چیست ؟

در بخش قبل اصل پاسکال را فرا گرفتیم. بر طبق این اصل، فشار خارجی وارد شده به مایعی داخل ظرف، در سراسر مایع به صورت یکنواخت و برابر پخش می‌شود. توجه به این نکته مهم است که اصل پاسکال، تنها برای فشارهای خارج از شاره صدق می‌کند. سوال مهمی که ممکن است مطرح شود آن است که در مورد فشار در عمق مشخصی از شاره (مایع) چه می‌توانیم بگوییم. به طور حتم این موضوع را تجربه کرده‌اید یا شنیده‌اید که به هنگام شنا در دریا یا استخر، هرچه در عمق عمیق‌تری شنا کنید، فشار وارد شده بر شما بیشتر خواهد بود.

در این بخش می‌خواهیم فشار را در عمق مشخصی از مایع به‌دست آوریم. ظرفی به شکل استوانه داریم که با مایعی دلخواه مانند آب پر شده است. فرض کنید ظرف روی سیاره‌ای بدون اتمسفر، اما با جرمی برابر جرم زمین قرار دارد. بنابراین، قسمت خالی ظرف، خلأ است.

از آنجا که جرم سیاره و زمین با یکدیگر برابر هستند، شتاب جاذبه آن‌ها نیز با یکدیگر برابر خواهد بود. لایه‌ای نازک درون مایع را در نظر می‌گیریم که تمام سطح مقطع استوانه را به شکل نشان داده شده در تصویر زیر پر کرده است. این لایه در ارتفاع h از سطح مایع قرار دارد. از آنجا که شاره، مایع، کاملا ساکن و پایدار است، لایه انتخاب شده نیز کاملا بدون حرکت خواهد بود. از فیزیک پایه می‌دانیم برایند نیروهای وارد بر جسم ساکن یا جسمی که با سرعت ثابت حرکت می‌کند برابر صفر خواهد بود.

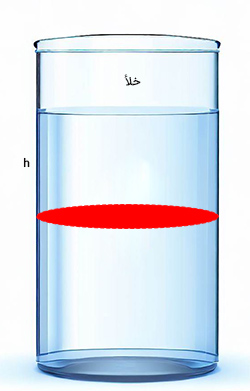
از این‌رو، مجموع نیروهای وارد شده به لایه به سمت پایین باید برابر مجموع نیروهای وارد شده به آن به سمت بالا باشد. نیروی وارد شده به سمت پایین بر لایه برابر وزن مایع بالای آن است:

$$F_ { down } = m_ l \times g$$

جرم $$m_l$$ چه مقدار است؟ برای به‌دست آوردن این جرم از مفهومی به نام چگالی استفاده می‌کنیم. چگالی به صورت نسبت جرم به حجم تعریف می‌شود:

$$\rho = \frac { m } { V } \\ m = \rho V$$

در نتیجه،‌ نیرو به سمت پایین برابر است با:

$$F_ D = \rho _ l . V_ l . g$$

حجم مایعِ بالای لایه قرمزرنگ نیز برابر حاصل‌ضرب سطح مقطع استوانه در ارتفاع مایعِ بالای لایه است:

$$F_ D = \rho _ l . A h . g$$

مقدار نیروی رو به پایین را به‌دست آوردیم. برای به‌دست آوردن مقدار فشار، کافی است طرفین رابطه $$F_ D = \rho _ l . A h . g$$ را بر مساحت سطح مقطع استوانه تقسیم کنیم:

$$\frac { F_ D } { A } = \rho_ l g h \\ P _ D = \rho _ l g h$$

از آنجا که نیروی رو به پایین برابر نیروی رو به بالا است، فشار رو به پایین نیز برابر فشار رو به بالا خواهد بود.

مکانیک شاره چیست ؟

در بخش قبل فهمیدیم شاره چیست و در مورد مهم‌ترین ویژگی‌های آن مانند فشار صحبت کردیم. در این بخش در مورد مکانیک شاره‌ها صحبت می‌کنیم. مکانیک شاره‌ها بخشی از علم فیزیک است که در آن در مورد اثر نیرو بر شاره و اثرات آن صحبت می‌کنیم. منظور از اثر، جهت و اندازه نیروی وارد شده است. به عنوان مثال، توپ فوتبالی را در نظر بگیرید که بدون حرکت روی زمین قرار گرفته است. ضربه‌ای به آن وارد می‌کنید. در اثر ضربه، نیرویی به توپ وارد می‌شود. سپس، توپ در راستای نیروی وارد شده بر آن شروع به حرکت می‌کند. در مکانیک شاره‌ها در مورد رفتار شاره‌ها پس از اعمال نیرو صحبت می‌کنیم.

مکانیک شاره‌ها را می‌توان به سه بخش کلی تقسیم کرد:

• استاتیک شاره‌ها: کلمه استاتیک به معنای حالت سکون است. بنابراین در این شاخه از مکانیک شاره‌ها، سیال را در حالت سکون بررسی می‌کنیم.
• سینماتیک شاره‌ها: به مطالعه شاره به هنگام حرکت و نادیده گرفتن نیروهای فشاری،‌ سینماتیک شاره گفته می‌شود.
• دینامیک شاره‌ها: به مطالعه شاره به هنگام حرکت همراه با در نظر گرفتن نیروهای فشاری،‌ دینامیک شاره گفته می‌شود.

استاتیک شاره چیست ؟

در فیزیک کلاسیک، فیزیک حاکم بر اجسام مختلف با توجه به جرم آن‌ها توصیف می‌شود، اما برای شاره‌ها از کمیت متفاوتی به نام چگالی استفاده می‌کنیم. به طور حتم در فیزیک دبیرستان با این کمیت آشنا شده‌اید. چگالی به صورت نسبت جرم به حجم اشغال شده توسط آن جرم تعریف می‌شود . واحد اندازه‌گیری آن برابر کیلوگرم بر مترمکعب است. اگر جسمی جامد یا شاره‌ای مشخص از اتم‌های و مولکول‌های سنگین‌تر ساخته شده باشند یا ذرات تشکیل‌دهنده آن‌ها در فاصله بسیار نزدیک‌تری از یکدیگر قرار داشته باشند، چگالی جسم جامد یا شاره بیشتر خواهد بود. شاره‌ها مشخصه مهم دیگری به نام فشار نیز دارند. فشار به صورت نسبت نیرو به مساحت اعمال نیرو، تعریف می‌شود و واحد اندازه‌گیری آن پاسکال یا نیوتن بر مترمربع است.

شاره‌ها در تمامی جهت‌ها فشار وارد می‌کنند. فشار متوسط هوا در سطح دریا برابر ۱۰۱۳۲۵ پاسکال است. به هنگام شنا در استخر، آب به شما فشار وارد می‌کند. اگر از ارتفاع مشخصی داخل استخر شیرجه بزنید، فشار آب را به خوبی احساس خواهید کرد. همچنین، با افزایش عمق، مقدار فشار وارد شده نیز افزایش می‌یابد. زیر در عمق‌های بیشتر، وزن بیشتری از آب بالای سرِ ما قرار دارد. در مطالب بالا در مورد ارتباط فشار و عمق صحبت کردیم. فیزیک‌دانی به نام پاسکال در قرن هفدهم میلادی به قانونی جالب در مورد شاره‌های محبوس رسید، اگر به شاره‌ای محبوس فشار وارد کنیم، فشار در هم ناحیه از شاره به اندازه فشار اعمال شده، افزایش خواهد یافت.

به عنوان مثال، فرض کنید لیوانی پر از آب داریم. با استفاده از پیستونی متحرک می‌خواهیم فشاری برابر ۱۰۰۰۰ پاسکال بر سطح آب وارد کنیم. پس از اعمال این فشار به سطح آب، فشار در همه جای آب به همین میزان افزایش خواهد یافت. به این قانون، اصل پاسکال گفته می‌شود.

سینماتیک شاره چیست ؟

در بخش قبل در مورد شاره‌های ساکن صحبت کردیم، در این بخش در مورد شاره‌های متحرک به اختصار صحبت می‌کنیم. گرچه ما در جهانی فیزیکی زندگی می‌کنیم که توسط قوانین حاکم بر فیزیک توصیف می‌شود، گاهی لازم است از برخی رویدادها چشم‌پوشی کنیم. به عنوان مثال، گاهی برای حل راحت‌تر مسائل فیزیکی از نیروی اصطکاک بین اجسام مختلف صرف‌نظر می‌کنیم. این مورد در شاره‌ها نیز صدق می‌کند. حرکت شاره‌ها، دینامیک است و اتفاقات مختلفی هم‌زمان به هنگام حرکت شاره رخ می‌دهند. برای درک بهتر دینامیک شاره‌ها، از برخی از این رویدادها صرف‌نظر می‌کنیم:

• شاره را تراکم‌ناپذیر در نظر می‌گیریم. به بیان دیگر، فرض می‌کنیم چگالی آن تغییر نمی‌کند.
• جریان شاره را کاملا هموار در نظر می‌گیریم. به بیان دیگر گرانروی شاره را برابر صفر یا بسیار کوچک در نظر می‌گیریم.

فرض کنید لوله‌ای بلند داریم که آب در آن به صورت هموار جریان دارد. جریان آب از دو شرط گفته شده به طور کامل پیروی می‌کند. لوله در قسمت انتهایی باریک‌تر می‌شود. با باریک‌تر شدن لوله، جریان آب تحت‌تاثیر قرار می‌گیرد. تنها چیزی که با باریک شدن لوله تغییر نمی‌کند، جرم آب عبوری از مساحت داده شده در سطح لوله برحسب زمان (آهنگ شارش جرم) است. بنابراین، آهنگ شارش جرم در همه جای لوله یکسان است. دلیل این موضوع آن است که آب به هنگام حرکت در لوله، مابقی آب داخل لوله را نیز به همراه خود حرکت می‌دهد. قسمتی از لوله را در نظر بگیرید که در هر ثانیه، یک کیلوگرم آب از آنجا عبور می‌کند. به همین دلیل،‌ در بقیه قسمت‌های لوله نیز، یک کیلوگرم آب در مدت زمان یک ثانیه عبور می‌کند.

نرخ شارش جرم در نقطه‌ای از شاره برابر نرخ شارش جرم در هر نقطه‌ دیگری از شاره است که معادله ریاضی آن به صورت زیر نوشته می‌شود و معادله پیوستگی نام دارد:

$$\frac { \triangle m_1 } { \triangle t } = \frac { \triangle m _ 2 } { \triangle t }$$

سرعت جریان شاره به مساحت سطح مقطع لوله‌ای که در آن قرار دارد بستگی دارد. فرض کنید مهندسِ شهری خیالی هستید و می‌خواهید آهنگ شارش آب را در نقطه‌ای مشخص در سیستم آب شهری به‌دست آورید. جرم عبوری در هر لحظه را از قسمت موردنظر نمی‌دانیم. تنها سطح مقطع و سرعت عبور آب در نقطه مشخص شده از لوله را می‌دانیم. ابتدا به سطح مقطع لوله در نقطه موردنظر نگاه می‌کنیم. جرم شاره عبوری از این سطح مقطع برابر حاصل‌ضرب چگالی در حجم است:

$$\triangle m = \rho \triangle V$$

حجم $$\triangle V$$ نیز برابر حاصل‌ضرب مساحت سطح مقطع در مسافت طی شده توسط شاره است:

$$\triangle V = A \triangle l$$

همچنین، سرعت، برابر نسبت مسافت طی شده توسط شاره بر زمان است:

$$v = \frac { \triangle l } { \triangle t }$$

با ترکیب سه معادله نوشته شده در بالا به شکل متفاوتی از معادله پیوستگی می‌رسیم:

$$\rho _ 1 A_ 1 v _ 1 = \rho _2 A_ 2 v _2$$

معادله به‌دست آمده به ما می‌گوید که حاصل‌ضرب چگالی، مساحت و سرعت در هر نقطه از شاره برابر حاصل‌ضرب این سه کمیت در هر نقطه دیگری در شاره است. بر طبق یکی از دو فرض در نظر گرفته شده، شاره تراکم‌ناپذیر و چگالی آن در همه‌ نقطه‌ها یکسان است. بنابراین، می‌توانیم چگالی را از طرفین رابطه $$\rho _ 1 A_ 1 v _ 1 = \rho _2 A_ 2 v _2$$ حذف کنیم:

$$A_ 1 v _ 1 =  A_ 2 v _2$$

معادله به‌دست آمده نیز به ما می‌گوید آهنگ شارش جرم در هر نقطه از سیال یکسان است،‌ با این تفاوت که به جای نوشتن رابطه برحسب جرم و زمان،‌ آن را برحسب سرعت و مساحت نوشته‌ایم. بر طبق معادله فوق، شاره در لوله‌های باریک با سرعت بیشتری حرکت می‌کند.

دینامیک شاره چیست ؟

در دینامیک شاره‌ نیز به شاره‌ها به هنگام حرکت توجه می‌کنیم. اما برخلاف سینماتیک شاره، در دینامیک شاره از نیروهای فشاری صرف‌نظر نمی‌کنیم.

ابر شاره چیست ؟

در مطالب بالا فهمیدیم تعریف کلی و تخصصی شاره چیست. عوامل مختلفی از جمله دما بر رفتار شاره تاثیر می‌گذارند. فرض کنید لیوانی چای دارید. آن را به هم بزنید و برای پنج دقیقه روی میز قرار دهید و سپس برگردید. داخل لیوان را نگاه کنید، چای هنوز می‌چرخد، چه حسی دارید؟ چرخش چای پس از ۵ دقیقه منطقی به نظر نمی‌رسد، اما اگر لیوان از هلیوم با دمای ۲۷۰- درجه سلسیوس پر شده باشد،‌ این اتفاق اصلا دور از ذهن نخواهد بود. هلیوم در این دما تبدیل به ماده‌ای بسیار عجیب به نام ابرشاره می‌شود. این پدیده سبب شد بسیاری از فیزیک‌دان‌های نظری و تجربی، برنده جایزه نوبل در سال‌های ۱۹۷۲ و ۱۹۹۶ و ۲۰۰۳ میلادی شوند.

برای آشنایی با رفتار ابرشاره‌ها، ابتدا باید بدانیم ذرات چگونه رفتار می‌کنند. از فیزیک کوانتوم می‌دانیم که اتم‌ها و مولکول‌ها نمی‌توانند انرژی با هر مقداری داشته باشند. انرژی اتم‌ها گسسته است. به بیان دیگر، اتم‌های و مولکول‌ها می‌توانند بین ترازهای گسسته انرژی با مقدارهای مشخص، جهش کنند.

دو تراز انرژی با مقدارهای $$E_1$$ و $$E_2$$ در نظر بگیرید. این دو تراز در فاصله مشخصی از یکدیگر قرار گرفته‌اند و هیچ تراز انرژی بین آن‌ها قرار ندارد. اتم‌ها می‌توانند در ترازهای انرژی $$E_1$$ یا $$E_2$$ قرار داشته باشند و بین این دو تراز نمی‌توانند قرار داشته باشند. اما در زندگی روزانه این اثر را نمی‌بینیم، زیرا اثرات بسیاری وجود دارند که بر اثرات کوانتومی سایه می‌اندازند. با کاهش دما با اتفاقات جالبی، به خصوص در مورد هلیوم، روبرو می‌شویم. در دماهای بسیار پایین، بیشتر مواد یخ می‌زنند و به شکل قطعه‌های یخ درمی آیند. اما هلیوم در میان عناصر مختلف استثنا محسوب می‌شود و هرگز یخ نمی‌زند. این عنصر در فشار اتمسفر با کاهش دما تا صفر مطلق، مایع باقی می‌ماند.

قبل از رسیدن به دمای صفر مطلق و در دمایی در حدود ۲۷۰- کلوین، هلیوم رفتار ماده را فراموش می‌کند. دلیل این موضوع آن است که با کاهش دما، انرژی اتم‌ها کاهش می‌یابد و به تراز انرژی پایین‌تر و یکسانی سقوط می‌کنند. در این جا است که داستان عجیب و غیرقابل‌باور می‌شود. بر طبق قوانین فیزیک کوانتوم، اتم‌های در تراز انرژی یکسان، رفتار مشابهی را از خود نشان می‌دهند. اتم‌ها از دیدگاه ریاضی غیرقابل‌تشخیص از یکدیگر می‌شوند و رفتار یمسانی دارند. در این حالت، اتم‌ها دیگر در جهت‌های مختلف حرکت و به یکدیگر برخورد نمی‌کنند. در صفر مطلق، هلیوم مایع به ابرشاره هلیوم تبدیل می‌شود. همه اتم‌ها هم‌جهت و هم‌زمان با یکدیگر حرکت می‌کنند. بنابراین، اصطکاک بین اتم‌ها برابر صفر می‌شود.

مایعاتی مانند آب پس از ریختن داخل لیوان یا هر ظرفی، تمایل به بالا رفتن از دیواره‌های ظرف دارند. اما در بیشتر مواقع، اصطکاک بین دیواره‌ها و مایع به اندازه‌ای است که از بالا رفتن بیشتر مایع از دیواره‌ها جلوگیری کند. این حالت برای ابرشاره‌ها صدق نمی‌کند. ابرشاره به راحتی از دیواره ظرف بالا می‌رود و از آن عبور می‌کند. به این نکته توجه داشته باشید که این اثر برای هر اتم هلیوم صادق نیست، بلکه ابرشارگی را تنها می‌توانیم در اتم‌های هلیوم ۴ مشاهده کنیم. هلیوم ۴، دو پروتون و دو نوترون دارد. این آرایش سبب می‌شود که اتم‌های هلیوم ۴ همانند ذراتی به نام بوزون‌ها رفتار کنند. بوزون‌ها می‌توانند هم‌زمان در تراز انرژی مشابهی قرار بگیرند. در صورتی که ذراتی مانند الکترون‌ها، رفتار کاملا متفاوتی را از خود نشان می‌دهند.

الکترون‌ها همانند ذراتی به نام فرمیون‌ها رفتار می‌کنند و تنها دو الکترون با عدد‌های کوانتومی متفاوت می‌توانند تراز انرژی مشابهی را اشغال کنند.

انواع شاره چیست ؟

در ابتدای بخش فهمیدیم شاره ماده‌ای است که پس از اعمال نیرو بر آن به صورت پیوسته جاری می‌شود. به گاز، مایع و پلاسما، شاره می‌گوییم. گاهی جامد پلاستیکی را نیز به عنوان شاره در نظر گرفته می‌شود. شاره‌ها براساس ویژگی‌های آن‌ها به انواع زیر تقسیم‌بندی می‌شوند:

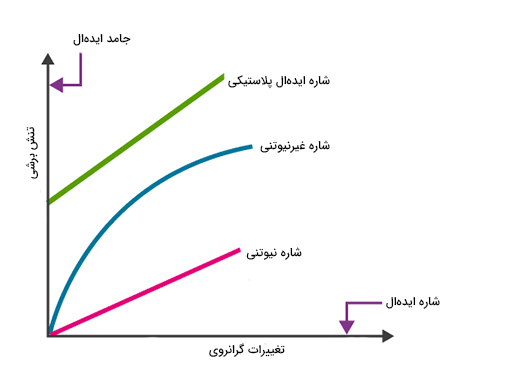
• شاره‌ ایده‌آل: شاره‌ ایده‌آل گرانروی یا ویسکوزیته ندارد و تراکم‌ناپذیر است. این شاره در شرایط عادی نمی‌تواند وجود داشته باشد.
• شاره واقعی: تمام شاره‌هایی که گرانروی دارند در گروه شاره‌های واقعی قرار می‌گیرند.
• شاره نیوتنی: به شاره واقعی که از قانون ویسکوزیته نیوتن پیروی می‌کند، مانند آب و هیدروژن، شاره نیوتنی گفته می‌شود.
• شاره غیرنیوتنی: به شاره‌هایی که از قانون ویسکوزیته نیوتن پیروی نمی‌کنند، شاره غیرنیوتنی گفته می‌شود.
• شاره پلاستیکی ایده‌آل: اگر در شاره‌ای تنش برشی با تغییرات سرعت متناسب باشد، به این شاره، شاره پلاستیکی ایده‌آل می‌گوییم.
• شاره تراکم‌ناپذیر: اگر چگالی مایع با اعمال نیرو تغییر نکند، به این شاره، شاره تراکم‌ناپذیر گفته می‌شود.
• شاره تراکم‌پذیر: اگر چگالی مایع با اعمال نیرو تغییر کند، به این شاره، شاره تراکم‌پذیر گفته می‌شود.

در بخش قبل فهمیدیم انواع شاره چیست. شاره‌ها با توجه به ویژگی‌های آن‌ها به انواع مختلفی تقسیم می‌شوند. یکی از ویژگی‌های مهم شاره‌ها وارد کردن نیروی اصطکاک به اجسام درون آن است. به این نیرو، نیروی مقاومت شاره می‌گوییم.

نیروی مقاومت شاره چیست ؟

به نیروی مقاومت وارد شده از سمت شاره، مایع یا گاز، بر جسم، نیروی مقاومت شاره یا نیروی درگ گفته می‌شود. هنگامی‌که توپی را داخل استخر پر از آبی می‌اندازیم، نیروی اصطکاکی از طرف آب بر توپ وارد می‌شود و از حرکت آسان توپ در آب جلوگیری می‌کند. آب مایع است. سوال مهمی که ممکن است مطرح شود آن است که آیا هوا، به عنوان گاز نیز، بر توپ به هنگام حرکت نیروی اصطکاکی در خلاف جهت حرت آن وارد می‌کند یا خیر. بله، اگر توپ از ارتفاع مشخصی از سطح زمین رها شود، به هنگام حرکت به سمت زمین، نیروی مقاومتی از سمت هوا در جهت مخالف بر آن وارد می‌شود. ب نیروی مقاومت شاره به عامل‌های زیر بستگی دارد:

• ماهیت شاره: نیروی مقاومت آب بیشتر از نیروی مقاومت هوا است.
• گرانروی: هر چه ویسکوزیته شاره‌ای بزرگ‌تر باشد، نیروی مقاومت شاره نیز بزرگ‌تر خواهد بود.
• سرعت حرکت جسم در شاره: هرچه جسم با سرعت بیشتری در شاره حرکت کند، نیروی مقاومت بزرگ‌تری را از طرف شاره احساس می‌کند.
• شکل جسم: شکل جسم بر مقدار مقاومتی که جسم از طرف شار احساس می‌کند تاثیر می‌گذارد.

جمع‌بندی

در این مطلب از مجله فرادرس، ابتدا به پرسش شاره چیست به زبان ساده پاسخ دادیم. در ادامه، در مورد مهم‌ترین ویژگی‌های شاره‌ها مانند چگالی، حجم مخصوص، چگالی نسبی، وزن مخصوص، فشار، کشش سطحی و گرانروی صحبت کردیم. در پایان، انواع شاره‌ها را براساس مشخصه‌های آن‌ها توضیح دادیم.