طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال

طول ضلع مربع فاصله بین دو گوشه مجاور در این شکل هندسی است. مربع، چهار ضلع با اندازههای مساوی دارد. اندازه این چهار ضلع، به منظور محاسبه محیط و مساحت مورد استفاده قرار میگیرد. طول مربع با محیط آن متناسب است. در این آموزش، به معرفی مفهوم، روشهای محاسبه و نسبت طول ضلع مربع به محیط آن میپردازیم و چند مثال مرتبط را حل میکنیم.
مربع چیست؟
مربع، یک چهار ضلعی منتظم است که چهار ضلع هماندازه و چهار زاویه راست (90 درجه) دارد.
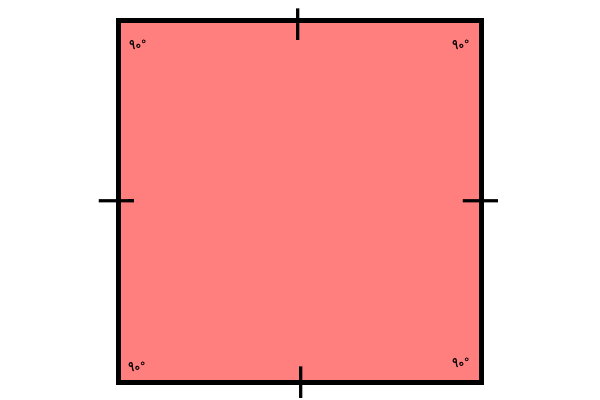
اجزای مربع چه هستند؟
مربع، شکلی است که از چهار ضلع، چهار راس (گوشه)، چهار زاویه داخلی، چهار زاویه خارجی و دو قطر تشکیل میشود.
ضلع مربع چیست؟
ضلع، پارهخطی است که دو راس مجاور در یک چندضلعی را به یکدیگر وصل میکند. ضلعها، اصلیترین معیار اندازهگیری محیط هستند. محدوده داخل ضلعها، مساحت مربع را نمایش میدهد. در تصویر زیر، ضلعهای یک مربع مشخص شدهاند.
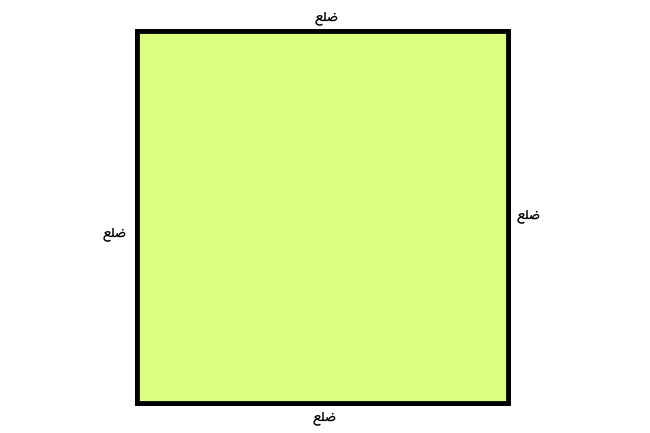
طول ضلع مربع چیست؟
طول ضلع مربع فاصله بین دو راس مجاور آن است. مربع، یکی از چندضلعیهای منتظم در نظر گرفته میشود. در این نوع چندضلعیها، طول تمام ضلعها با هم برابرند. به همین دلیل، برای انجام محاسبات مربوط به مربع، داشتن اندازه یکی از ضلعها کفایت میکند.

طول ضلع مربع چه کاربردی دارد؟
طول ضلع مربع به منظور محاسبه محیط و مساحت مربع مورد استفاده قرار میگیرد. البته استفاده از ضلع مربع برای محاسبه قطر (فاصله بین دو راس مقابل) نیز کاربرد دارد. در بخشهای بعدی، روابط بین طول ضلع مربع با دیگر اندازههای این شکل هندسی را معرفی میکنیم و به حل چند مثال میپردازیم.
محیط مربع با ضلع چگونه بدست میآید؟
محیط مربع، مسافت روی ضلعهای آن است. اگر اندازه هر چهار ضلع مربع را با هم جمع کنیم، محیط مربع به دست میآید. فرمول محیط مربع به زبان فارسی عبارت است از:
ضلع + ضلع + ضلع + ضلع = محیط مربع

به دلیل برابر بودن اندازه هر چهار ضلع مربع، میتوانیم فرمول محیط مربع را به صورت زیر بازنویسی کنیم:
ضلع × 4 = محیط مربع
در نتیجه، محیط مربع از «طول ضلع مربع ضربدر چهار» به دست میآید.
محیط مربع با عبارت جبری
عبارت جبری یا فرمول ریاضی محیط مربع به صورت زیر نوشته میشود:
در فرمول بالا، A، مساحت مربع و a، طول ضلع مربع را نمایش میدهد.
مثال 1: محاسبه طول ضلع مربع از روی محیط
محیط یک مربع برابر 24 متر است. طول هر ضلع را حساب کنید.
به منظور تعیین طول ضلع مربع، از فرمول محیط استفاده میکنیم:
ضلع × 4 = محیط مربع
ضلع × 4 = 24
4 ÷ 24 = ضلع
6 = ضلع
بر اساس مراحل بالا دیدیم که طول ضلع مربع برابر اندازه محیط تقسیم بر چهار است.
فرمول طول ضلع مربع با محیط
برای به دست آوردن رابطه محاسبه ضلع مربع، ابتدا فرمول محیط را مینویسیم:
ضلع × 4 = محیط مربع
با بازنویسی رابطه بالا بر حسب ضلع، خواهیم داشت:
4 ÷ محیط مربع = ضلع
یا
نسبت طول ضلع مربع به محیط آن چیست؟
نسبت طول ضلع مربع به محیط آن برابر یک چهارم است. این نسبت با توجه به فرمول محیط مربع به دست میآید. برای درک بهتر این نسبت، به حل یک مثال میپردازیم.
مثال 2: محاسبه نسبت طول ضلع مربع به محیط آن
در جدول زیر، طول ضلع چندین مربع آورده شده است. محیط هر یک از این مربعها را حساب کرده و نسبت طول ضلع به محیط آنها را به دست بیاورید. از این مثال چه نتیجهای میگیرید.
| طول ضلع مربع |
| 1 |
| 2 |
| 0/5 |
| 4 |
| 1/5 |
| 10 |
| 100 |
نتیجه محاسبه محیط هر یک از مربعها و نسبت طول ضلع آنها به محیط را در جدول زیر آوردهایم.
| طول ضلع مربع | محیط مربع | نسبت طول ضلع مربع به محیط آن |
| 1 | 4 = 1 × 4 | 0/25 = 4 ÷ 1 |
| 2 | 8 = 2 × 4 | 0/25 = 8 ÷ 2 |
| 0/5 | 2 = 0/5 × 4 | 0/25 = 2 ÷ 0/5 |
| 4 | 16 = 4 × 4 | 0/25 = 16 ÷ 4 |
| 1/5 | 6 = 1/5 × 4 | 0/25 = 6 ÷ 1/5 |
| 10 | 40 = 10 × 4 | 0/25 = 40 ÷ 10 |
| 100 | 400 = 100 × 4 | 0/25 = 400 ÷ 100 |
همانطور که مشاهده میکنید، در هر حالت، نسبت طول ضلع مربع به محیط آن برابر 025 یا همان یکچهارم است. با توجه به این مثال میتوانیم نتیجه بگیریم که طول ضلع مربع با محیط آن متناسب است.
مساحت مربع با ضلع چگونه بدست میآید؟
سطح درون ضلعهای مربع، با کمیتی به اسم مساحت اندازهگیری میشود. اگر دو ضلع مربع را در هم ضرب کنیم، مساحت آن به دست میآید. فرمول مساحت مربع به زبان فارسی عبارت است از:
خودش × یک ضلع = مساحت مربع

با توجه به فرمول مساحت با ضلع میتوان گفت که طول ضلع مربع با مساحت آن متناسب نیست. برای تایید این موضوع، در بخشهای بعدی به حل یک مثال خواهیم پرداخت.
مساحت مربع با عبارت جبری
فرمول ریاضی یا عبارت جبری مساحت مربع با ضلع به صورت زیر نوشته میشود:
- A: مساحت مربع
- a: طول ضلع مربع
فرمول طول ضلع مربع با مساحت
اگر فرمول مساحت مربع با ضلع را بر حسب ضلع بازنویسی کنیم، رابطه زیر به دست میآید:
این رابطه، فرمول محاسبه طول ضلع مربع با مساحت است.
مثال 3: محاسبه طول ضلع مربع از روی مساحت
اگر مساحت یک مربع برابر 36 متر مربع باشد، طول ضلع آن چقدر است؟
بر اساس فرمول محاسبه ضلع مربع با مساحت داریم:
به جای A، اندازه مساحت را قرار میدهیم:
در نتیجه، اندازه ضلع مربع برابر 6 متر است.
مثال 4: تعیین نسبت طول ضلع مربع به مساحت آن
جدول زیر، طول ضلع چند مربع را نمایش میدهد. مساحت مربعها و نسبت طول ضلع به مساحت آنها را به دست بیاورید. از این مثال چه نتیجهای میگیرید؟
| طول ضلع مربع |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
نتیجه محاسبه مساحت و نسبت طول ضلع به مساحت را در جدول بعدی آوردهایم.
| طول ضلع مربع | مساحت مربع | نسبت طول ضلع مربع به مساحت آن |
| 3 | 9 = 3 × 3 | 0/33 = 9 ÷ 3 |
| 4 | 16 = 4 × 4 | 0/25 = 16 ÷ 4 |
| 5 | 25 = 5 × 5 | 0/2 = 25 ÷ 5 |
| 6 | 36 = 6 × 6 | 0/17 = 36 ÷ 6 |
| 7 | 49 = 7 × 7 | 0/14 = 49 ÷ 7 |
| 8 | 67 = 8 × 8 | 0/12 = 64 ÷ 8 |
| 9 | 81 = 9 × 9 | 0/11 = 81 ÷ 9 |
| 10 | 100 = 10 × 10 | 0/10 = 100 ÷ 10 |
همانطور که مشاهده میکنید. هیچ یک از نسبتهای طول ضلع به مساحت در مربعهای بالا با هم برابر نیستند. در نتیجه، برخلاف طول ضلع مربع با محیط آن، طول ضلع مربع با مساحت آن متناسب نیست.
نسبت طول ضلع مربع به قطر آن
قطر مربع، پارهخطی است که دو راس مقابل را به یکدیگر وصل میکند. مربعها، دو قطر دارند. با رسم هر یک از این قطرها، مربع به دو مثلث قائم الزاویه برابر تقسیم میشود. وترهای این مثلثها، معادل قطرهای مربع و ساقهای آنها، معادل ضلعهای مربع هستند.
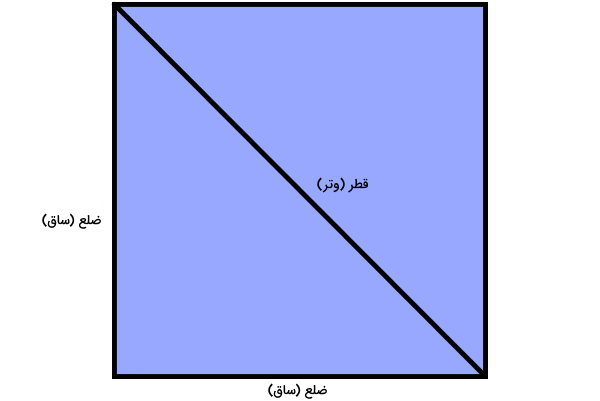
بر اساس قضیه فیثاغورس، رابطه زیر بین طول ضلع مربع و قطر آن برقرار است:
فرمول بالا، به منظور محاسبه قطر مربع از روی ضلع آن مورد استفاده قرار میگیرد. اگر این فرمول را بر حسب ضلع بازنویسی کنیم، به فرمول طول ضلع مربع با قطر میرسیم:
مثال 5: محاسبه ضلع مربع از روی قطر
قطر مربعی برابر 5 است. اندازه ضلع مربع را به دست بیاورید. (رادیکال 2 را برابر 1/4 در نظر بگیرید.)
برای حل مثال، فرمول ضلع مربع با قطر را مینویسیم و اندازه قطر را درون آن قرار میدهیم:
در نتیجه، اندازه ضلع مربع برابر 3/5 است.
سوالات متداول در رابطه با طول ضلع مربع
در این بخش، به برخی از سوالات پرتکرار در رابطه با طول ضلع مربع به طور خلاصه پاسخ میدهیم.
تعریف ضلع مربع چیست؟
ضلع مربع، پارهخطی است که دو گوشه مجاور را به یکدیگر وصل میکند.
تعریف طول ضلع مربع چیست؟
طول ضلع مربع، فاصله بین دو گوشه مجاور است.
نسبت طول ضلع مربع به محیط آن چند است؟
نسبت طول ضلع مربع به محیط آن برابر یکچهارم (0/25) است.
فرمول ضلع مربع بر حسب محیط چیست؟
فرمول ضلع مربع بر حسب محیط برابر «4 ÷ محیط مربع» یا «a=P÷4» است.
فرمول ضلع مربع بر حسب مساحت چیست؟
فرمول ضلع مربع بر حسب محیط برابر «مجذور مساحت» یا «a=√A» است.
فرمول ضلع مربع بر حسب قطر چیست؟
فرمول ضلع مربع بر حسب قطر برابر «2÷(2√d)=a» است.
طول ضلع مربع با چه چیزی تناسب دارد؟
ضلع مربع با محیط آن تناسب دارد.
طول ضلع مربع با چه چیزی تناسب ندارد؟
ضلع مربع با مساحت آن تناسب ندارد.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مربع — تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مربع چیست ؟ — تعریف و مفاهیم به زبان ساده (+ فیلم آموزش رایگان)
- قطر مربع چیست و چگونه بدست می آید ؟ — به زبان ساده + حل تمرین و مثال
- چگونه محیط مربع را حساب کنیم؟ + فیلم آموزشی و حل تمرین
- مساحت مربع چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال(همین مطلب)
- فرمول محیط مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول مساحت مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع داخل دایره چگونه بدست می آید ؟ — به زبان ساده + تمرین و مثال
- مساحت مربع با قطر چگونه بدست می آید ؟ – به زبان ساده + حل تمرین و مثال













خیلی خوب یاد داده است.
از استادان و دست اندرکاران فرادرس ممنونم.
سلام و وقت بخیر؛
از اینکه این آموزش برای شما مفید واقع شد، بسیار خرسندیم.
از همراهی شما با مجله فرادرس، سپاسگزاریم. سلامت و موفق باشید.