شمارنده MOD — از صفر تا صد (+ دانلود فیلم آموزش رایگان)
شمارنده MOD یا Modulus Counter یک مدار شمارنده آبشاری است که قبل از ریست شدن، تا یک مقدار تنظیم شده میشمارد. در این آموزش قصد داریم این نوع از شمارندهها را بررسی کنیم.
وظیفه یک شمارنده این است که با هر پالس کلاک، در دنباله اعداد از پیش تعیین شده پیشروی کند، تا شمارش انجام گیرد. شمارندههایی که دنباله اعداد یا حالتهای شمارش خود را با ورود هر پالس ساعت افزایش میدهند، در اصطلاح شمارنده بالا شمار (Up Counter) یا صعودی نام دارند. به طریق مشابه، شمارندههایی که با ورود پالس کلاک به آنها، دنباله اعداد یا حالتهای شمارش خود را کاهش میدهند، شمارنده پایین شمار (Down Counting) یا نزولی گفته میشوند. شمارندههایی که این قابلیت را دارند تا در هر دو مود بالا شمار و پایین شمار عمل کنند، شمارندههای دو جهته (Bidirectional Counters) نام دارند.
در حالت کلی میتوان گفت که شمارندهها، مدارات منطقی ترتیبی (Sequential Logic Circuit) هستند که توسط یک سیگنال خارجی به نام سیگنال کلاک، تریگر یا فعالسازی میشوند. یک شمارنده میتواند به نحوی ساخته شود تا به عنوان یک مدار سنکرون و یا یک مدار آسنکرون عمل کند. در شمارندههای سنکرون، تمام بیتهای شمارش به صورت همزمان و با اعمال سیگنال کلاک تغییر میکنند. در حالی که در یک شمارنده آسنکرون، مدار از سیگنال کلاک ورودی مستقل است و به همین دلیل بیتهای داده، حالت خود را در زمانهای مختلف یکی پس از دیگری تغییر میدهد.
پس شمارندهها مدرات ترتیبی هستند که دنباله از پیش تعیین شدهای از حالتهای شمارش را دنبال میکنند و با سیگنال کلاک خارجی تریگر میشوند. تعداد حالتها یا دنباله شمارشی که یک شمارنده، قبل از بازگشت به حالت اصلی خود، طی میکند را پیمانه (Modulus) آن شمارنده میگویند و با MOD نشان داده میشود. به عبارت دیگر میتوان گفت که پیمانه هر شمارنده، تعداد اعدادی است که یک شمارنده میشمارد و برابر با عدد مقسم شمارنده است.
شمارندههای پیمانهای یا منقطع یا MOD بر اساس تعداد حالاتی که شمارنده در هر تکرار طی میکند، تعریف میشوند. به عنوان مثال، یک شمارنده دو بیتی که از ۰۰ تا ۱۱ در مبنای باینری میشمارد، دارای مقدار پیمانهای یا MOD برابر با ۴ است. مقادیر شمارش این شمارنده در مبنای ده دهی از ۰ تا ۳ است و حالتهایی که در طول شمارش آنها را طی میکند، برابر با ۰۰، ۰۱، ۱۰ و ۱۱ هستند. بعد از طی کردن این 4 حالت در دنباله شمارشی، شمارنده به حالت اصلی خود یعنی ۰۰ باز میگردد. بر اساس این توضیحات، چنین شمارندهای را شمارنده MOD-4 میگویند. به این نکته مهم نیز توجه کنید که این شمارنده برای طی کردن یک دنباله از ۰۰ تا ۱۱ به چهار پالس کلاک در ورودی خود احتیاج دارد.
همان طور که در مثال ساده بالا دیدیم، این شمارنده فقط دو بیت (n=2) دارد، بنابراین بیشینه تعداد حالتهای ممکن در خروجی برای این شمارنده برابر با $$ 2^n = 2^2 = 4 $$ است. اما نکته مهمی که وجود دارد، این است که میتوان شمارندهها را به نحوی طراحی کرد که شمارش را نه به صورت کامل، بلکه تا هر عدد دلخواهی از $$ 2^n $$ حالت ممکن، انجام دهند. این کار را با اتصال آبشاری چندین طبقه شمارنده به یکدیگر و تولید یک شمارنده MOD-N امکانپذیر میشود.
بنابراین یک شمارنده MOD-n، به n عدد فلیپ فلاپ که به یکدیگر متصل شده باشند، نیاز دارد تا یک بیت داده را بشمارد و $$ 2^n $$ حالت مختلف را در خروجی تولید کنند. n برابر با تعداد بیتها است. همچنین به این نکته باید توجه کرد که n همیشه یک عدد صحیح است.
دیدیم که یک شمارنده MOD دارای مقدار پیمانهای است که توان صحیحی از عدد ۲ مانند ۲، ۴، ۸ و ... در نظر گرفته میشود. بنابراین در تولید یک شمارنده n بیتی، بسته به تعداد فلیپ فلاپهای مورد استفاده و نیز نحوه اتصال آنها، نوع شمارنده و مقدار MOD آن تعیین میشود.
شمارنده MOD با فلیپ فلاپ نوع D
شمارندههای MOD با استفاده از فلیپ فلاپها ساخته میشوند. یک فلیپ فلاپ به تنهایی، میتواند دنباله شمارش متشکل از ۰ و ۱ را تولید کند و به عبارت دیگر دارای بیشینه شمارش برابر با ۲ است. انواع مختلفی از فلیپ فلاپها با طراحیهای متفاوتی وجود دارند که با استفاده از آنها میتوان یک شمارنده را ایجاد کرد. فلیپ فلاپهای SR، فلیپ فلاپهای JK، فلیپ فلاپهای JK Master-slave فلیپ فلاپهای نوع D و در نهایت فلیپ فلاپهای نوع T را میتوان به عنوان فلیپ فلاپهای مورد استفاده در ساخت شمارندهها نام برد. اما برای ساختار سادهتر میتوان این شمارندهها را با استفاده از فلیپ فلاپ نوع D ایجاد کرد. این فلیپ فلاپ را لچ داده نیز میگویند.
فلیپ فلاپ نوع D، فقط یک داده ورودی تکی و سیگنال کلاک خارجی را مورد استفاده قرار میدهد و همچنین این فلیپ فلاپ، حساس به لبه مثبت یا بالا رونده است.
فلیپ فلاپهای نوع D، مانند آیسی TTL 74LS74 را میتوان با استفاده از فلیپ فلاپهای حساس به لبه نوع JK و یا فلیپ فلاپهای SR ایجاد کرد. انتخاب فلیپ فلاپها به این موضوع بستگی دارد که طراح بخواهد که فلیپ فلاپ در لبه مثبت یا بالا رونده (تغییر سطح از ۰ به ۱) پالس کلاک تغییر حالت بدهد یا این کار را در لبه پایین رونده یا منفی (تغییر سطح از ۱ به ۰) پالس کلاک انجام دهد. در این مقاله فرض میکنیم که طراح بخواهد در لبه پایین رونده یا منفی پالس کلاک تغییر حالت دهد.
نماد مداری و جدول درستی فلیپ فلاپ نوع D در شکل زیر نشان داده شده است.

عملکرد فلیپ فلاپ نوع D بسیار ساده است؛ زیرا این نوع فلیپ فلاپ فقط یک ورودی داده D و یک ورودی اضافی پالس کلاک CLK دارد. این ساختار اجازه میدهد که یک بیت داده تکی (۰ یا ۱) تحت کنترل سیگنال کلاک فلیپ فلاپ ذخیرهسازی شود. به همین دلیل میتوان گفت که فلیپ فلاپ نوع D یک وسیله سنکرون است؛ زیرا دادهای که در ورودی آن باشد، فقط در لبه تریگر کننده پالس کلاک به خروجی فلیپ فلاپ منتقل میشود.
با توجه به جدول درستی فلیپ فلاپ نوع D، اگر یک سطح منطقی ۱ یا HIGH در ورودی داده فلیپ فلاپ قرار داشته باشد، با اعمال پالس کلاک مثبت، فلیپ فلاپ ست (Set) میشود و سطح منطقی یک را در خروجی Q ذخیره میکند. همچنین در خروجی مکمل فلیپ فلاپ یعنی $$\overline{Q}$$، مقدار صفر منطقی ذخیره میشود. به طریق مشابه، اگر یک سطح ۰ منطقی در ورودی D فلیپ فلاپ قرار بگیرد، با اعمال پالس کلاک مثبت بعدی، فلیپ فلاپ ریست میشود و سطح صفر منطقی را در خروجی Q خود ذخیره میکند و مقدار $$\overline{Q}$$ به سطح یک منطقی تغییر مییابد.
بنابراین هنگام HIGH بودن ورودی کلاک، خروجی Q فلیپ فلاپ نوع D، به مقدار ورودی D پاسخ میدهد. زمانی که ورودی کلاک در سطح LOW منطقی قرار داشته باشد، حالت در خروجی Q هر مقداری که باشد (۰ یا ۱ منطقی)، تا زمان ورود پالس کلاک سطح HIGH بعدی، در همان مقدار نگه داشته میشود. بنابراین خروجی Q فقط زمانی تغییر حالت میدهد که ورودی پالس کلاک از سطح LOW یا صفر منطقی به HIGH یا یک منطقی تغییر یابد. به همین دلیل این فلیپ فلاپ نوع D، یک فلیپ فلاپ حساس به لبه مثبت است. به یاد داشته باشید که فلیپ فلاپ حساس به لبه منفی بسیار شبیه به همین نوع از فلیپ فلاپها کار میکند و تفاوت آنها در این است که این بار فلیپ فلاپ در لبه منفی یا پایین رونده پالس کلاک تریگر میشود. حال که با اصول کاری یک فلیپ فلاپ نوع D آشنا شدیم، به نحوه اتصال این فلیپ فلاپها جهت تشکیل یک شمارنده MOD میپردازیم.
شمارنده مقسم بر دو
فلیپ فلاپ نوع D حساس به لبه، یک بلوک پایهای و تطبیق پذیر برای ایجاد شمارندههای MOD و یا هر نوع دیگر از مدارات منطقی ترتیبی است. اگر مطابق شکل زیر، خروجی $$ \overline{Q} $$ هر فلیپ فلاپ را به ورودی D آن متصل کنیم و یک حلقه فیدبک در مدار ایجاد کنیم، آنگاه میتوانیم فلیپ فلاپ را به یک شمارنده مقسم بر دو تبدیل کنیم. توجه کنید که خروجی $$ \overline{Q} $$ فلیپ فلاپ دقیقا مکمل خروجی Q است.
مدار و نیز دیاگرام زمانبندی یک شمارنده مقسم بر دو را در تصویر زیر میتوان مشاهده کرد.
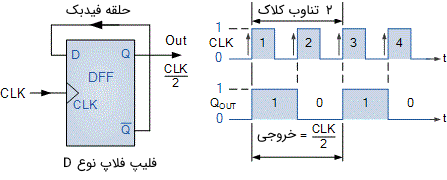
بر اساس دیاگرام زمانبندی این شمارنده، که در تصویر بالا دیده میشود، شکل موج خروجی Q دارای فرکانسی دقیقا برابر با نصف فرکانس کلاک ورودی است. بنابراین میتوان گفت که مدار مانند یک مقسم فرکانسی عمل میکند. اگر یک فلیپ فلاپ D دیگر را به مدار اضافه کنیم، به نحوی که خروجی Q فلیپ فلاپ اول را به ورودی فلیپ فلاپ دوم متصل کنیم، آنگاه فرکانس سیگنال خروجی فلیپ فلاپ دوم، برابر با یک چهارم فرکانس پالس کلاک ورودی خواهد بود. این روال را میتوان با اضافه کردن تعداد بیشتری فلیپ فلاپ به زنجیره ادامه داد. پس برای n عدد از فلیپ فلاپها که با روش بالا به یکدیگر متصل شده باشند، فرکانس خروجی در اثر تقسیمات متوالی بر ۲، نهایتا بر 2n تقسیم میشود.
به یاد داشته باشید که این روش تقسیم فرکانسی، برای استفاده در مدارات شمارنده بسیار مفید و ساده است. به عنوان مثال، اگر یک سیگنال ۶۰ هرتز به عنوان ورودی اصلی مدار در نظر گرفته شود، در نهایت با استفاده از مدار مقسم بر ۶۰ میتوانیم آن را به سیگنال زمانبندی با فرکانس ۱ هرتز تبدیل کنیم. ابتدا با استفاده از یک مقسم بر ۶ میتوانیم فرکانس ۶۰ هرتز ورودی را به ۱۰ هرتز کاهش دهیم و سپس از یک مقسم بر ۱۰ استفاده کنیم و خروجی را به فرکانس ۱ هرتز کاهش دهیم.
شمارنده MOD-4
به لحاظ تکنیکی، میتوان یک فلیپ فلاپ تکی را علاوه بر المان حافظه یک بیتی، یک شمارنده MOD-2 نیز در نظر گرفت. چون این المان فقط یک خروجی دارد، بنابراین با بهره گرفتن از پالس کلاک، منجر به شمارش دو حالت ۰ و ۱ میشود. یک فلیپ فلاپ تکی میتواند دنباله محدودی را شمارش کند، اما اگر تعداد بیشتری فلیپ فلاپ را به صورت زنجیری به هم متصل کنیم، میتوانیم ظرفیت شمارش را بالا ببریم و شمارندههای MOD با مقادیر مختلف را ایجاد کنیم.
اگر یک فلیپ فلاپ تکی را به عنوان شمارنده MOD-2 در نظر بگیریم، آنگاه با اضافه کردن فلیپ فلاپ دوم، شمارنده MOD-4 را خواهیم داشت که قادر است ۴ حالت گسسته را شمارش کند. عملکرد کلی این شمارنده این است که فرکانس سیگنال کلاک ورودی را بر ۴ تقسیم میکند. بنابراین دنباله شمارش برای این شمارنده دو بیتی MOD-4، متشکل از اعداد ۰۰، ۰۱، ۱۰ و ۱۱ است. دیاگرام زمانبندی و مدار شمارنده MOD-4 در شکل زیر نشان داده شده است.

به یاد داشته باشید که در دیاگرام زمانبندی بالا برای سادگی، گذارهای سوئیچینگ در $$ Q_A $$ و $$ Q_B $$ و CLK، به صورت همزمان نشان داده شدهاند. اگرچه این اتصالات نشاندهنده یک مدار شمارنده آسنکرون (Asynchronous) هستند، اما در عمل یک زمان تاخیر سوئیچینگ بسیار کوچک بین اعمال سیگنال کلاک با لبه مثبت یا بالا رونده و خروجیهای $$ Q_A $$ و $$ Q_B $$ وجود دارد. عملکرد این شمارنده آسنکرون دو بیتی را میتوان به کمک جدول درستی و دیاگرام حالت، به صورت تصویری نشان داد.
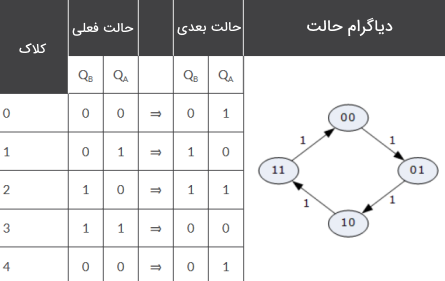
از جدول درستی بالا و با خواندن مقادیر $$ Q_A $$ و $$ Q_B $$، میتوانیم به این نکته پی ببریم که زمانی که $$ Q_A = 0 $$ و $$ Q_B = 0 $$ باشند، شمارش برابر با ۰۰ خواهد بود. بعد از اعمال پالس کلاک، مقادیر برابر با $$ Q_A = 1 $$ و $$ Q_B = 0 $$ خواهند شد و در نتیجه مقدار شمارش ۰۱ میشود.
اعمال پالس کلاکهای سوم و چهارم نیز باعث میشود که خروجی شمارنده به ۱۰ و ۱۱ تغییر یابد. حال پالس کلاک پنجم، شمارش را به مقدار اصلی ۰۰ ریست میکند. شمارنده پس از این حالت، تا زمانی که پالس کلاک دریافت کند، به صورت صعودی دنباله ۰۰، ۰۱، ۱۰، ۱۱ را تکرار میکند.
بنابراین دیدیم که یک شمارنده MOD-2 از یک فلیپ فلاپ تشکیل شده است و برای ساخت شمارنده MOD-4 به دو فلیپ فلاپ جهت شمارش ۴ حالت گسسته نیاز داریم. میتوانیم به سادگی فلیپ فلاپ دیگری را به انتهای زنجیره شمارنده MOD-4 اضافه کنیم تا یک شمارنده MOD-8 ایجاد شود. شمارنده MOD-8 دنبالهای متشکل از $$2^3 $$ حالت باینری، از ۰۰۰ تا ۱۱۱ را در خروجی برای کاربر ایجاد میکند و سپس به مقدار ۰۰۰ ریست میشود. این روند میتواند همچنان ادامه داشته باشد. مثلا ۴ فلیپ فلاپ قادر هستند که یک شمارنده MOD-16 را ایجاد کنند. مدار و دیاگرام حالت یک شمارنده MOD-8 در تصویر زیر نشان داده شده است.

بنابراین، میتوان شمارندههای MOD را برای ایجاد شمارشی طبیعی متشکل از $$ 2^n $$ حالت ایجاد کرد و سپس شمارنده به مقدار اولیه خود بازگشته و دنباله مجددا تکرار میشود. اما گاهی لازم است که یک شمارنده MOD ایجاد شود که در طول فرایند طبیعی شمارش، ریست شود و به حالت صفر اولیه بازگردد. به عبارت دیگر، عدد MOD شمارنده، توان کاملی از ۲ نباشد، بلکه اعدادی مانند ۳، ۵، ۶ یا ۱۰ باشد.
شمارنده MOD-m
شمارندهها (سنکرون و آسنکرون) در هر لحظه یک شمارش را در مجموعه اعداد باینری انجام میدهند. یک شمارنده n بیتی در حالت طبیعی به عنوان شمارنده با پیمانه $$ 2^n $$ عمل میکند. اما این امکان وجود دارد که شمارنده MOD را برای شمارش تا هر عدد دلخواه ایجاد کرد. برای این کار لازم است که از یک یا دو گیت منطقی خارجی اضافه در مدار شمارنده استفاده کنیم. این گیتهای منطقی باعث میشوند که شمارنده از بعضی از حالتهای خروجی صرف نظر کند و شمارش را در عدد دلخواه مورد نظر کاربر به پایان برساند و سپس به حالت صفر ریست شود. در حالت اول، خروجی Q تمام فلیپ فلاپها صفر است.
در این حالت شمارندهای که ایجاد میشود، یک شمارنده MOD-m است. این شمارنده تمام حالتهای ممکن را شمارش نمیکند، بلکه شمارش را تا حالت mام انجام داده و به صفر باز میگردد. واضح است که در اینجا m باید عددی کوچکتر از $$2^n $$ باشد. حال چگونه باید چنین شمارندهای را به وجود بیاوریم.
شمارندهها علاوه بر امکان شمارش رو به بالا و یا شمارش رو به پایین، ورودیهای اضافهای دارند که CLEAR و PRESET نام دارند. این ورودیها باعث میشوند که شمارنده بتواند شمارش را به صفر ریست کند (تمام Qها برابر با ۰) و یا شمارنده را در یک مقدار اولیه از پیش تعیینشده تنظیم میکنند. آیسی TTL 74LS74 دارای ورودی PRESET و ورودی CLEAR فعال در سطح پایین (Active-Low) است.
برای سادگی فرض کنید که ورودیهای CLEAR همگی به یکدیگر متصل شدهاند و از نوع ورودیهای Active-High هستند. در نتیجه، این ورودیها به فلیپ فلاپها اجازه میدهند تا زمانی که ورودی CLEAR برابر با ۰ یا سطح LOW است، عملکرد عادی داشته باشند. اما اگر ورودی CLEAR به سطح یک منطقی یا HIGH تغییر یابد، لبه مثبت بعدی پالس کلاک، تمام فلیپ فلاپها را بدون توجه به مقدار سیگنال کلاک بعدی، به حالت صفر (Q=0) ریست میکند.
به یاد داشته باشید که چون تمام ورودیهای CLEAR به یکدیگر متصل شدهاند، در نتیجه یک پالس تکی میتواند برای پاک کردن خروجیهای تمام فلیپ فلاپها به صفر مورد استفاده قرار گیرد. این کار قبل از شروع شمارش از این جهت ضروری است که اطمینان حاصل شود شمارش از مقدار ۰ شروع میشود. البته برخی شمارندهها با بیتهای بزرگتر، دارای پایه اضافه ENABLE یا INHIBIT نیز هستند که به شمارنده اجازه میدهند شمارش را در هر نقطه از چرخه شمارش متوقف کند و تا قبل از شروع مجدد شمارش، حالت کنونی خود را حفظ کند. در واقع چنین توانایی به این معنی است که شمارنده بدون اینکه الزاما به صفر ریست شود، متوقف (Stop) و سپس از همان نقطه شروع به کار (Start) کند.
یک شمارنده MOD-6
فرض کنید میخواهیم یک شمارنده MOD-۶ طراحی کنیم. نحوه انجام این کار به چه صورت خواهد بود؟
اولا میدانیم که m=۶ است، بنابراین $$2^n $$ باید از ۶ بزرگتر باشد. چون $$2^3 $$ برابر با ۸ و ۸ بزرگتر از ۶ است، بنابراین به یک شمارنده متشکل از ۳ فلیپ فلاپ نیاز داریم. این شمارنده در حالت طبیعی میتواند ۸ حالت شمارش، از ۰۰۰ تا ۱۱۱ باینری (از ۰ تا ۷ دسیمال) را ایجاد کند. با فرض شمارنده MOD-8 بالا، جدول درستی برای این شمارنده به صورت زیر خواهد بود.

برای ساخت یک شمارنده MOD-۶، باید شمارنده بعد از شمارش ۵ به صفر باز گردد. همان طور که در جدول درستی بالا هم میتوان دید، در حالت کار عادی، شمارش عدد شش باعث ایجاد $$ Q_A = 0 $$، $$ Q_B = 1 $$ و $$ Q_C = 1 $$ در خروجی میشود.
میتوانیم این حالت خروجی 110 (6) را به نحوی دیکود کنیم که یک سیگنال برای پاک کردن شمارنده و بازگشت به صفر تولید کند. برای این کار از یک گیت AND سه ورودی TTL 74LS11 و یک گیت NOT با آیسی TTL 74LS04 استفاده میکنیم. تصویری از نحوه اتصال این گیتهای منطقی به یکدیگر در شکل زیر نشان داده شده است.
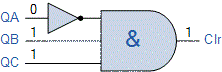
ورودیهای گیتهای منطقی NOT و AND به ترتیب به خروجیهای $$ Q_A $$ و $$ Q_B $$ و $$ Q_C $$ متصل میشوند. این اتصالات باعث میشوند که خروجی گیت AND برای تمام ترکیبات ورودیها، به جز حالتی که مد نظر ما است (110)، در سطح منطقی صفر یا LOW بماند. بنابراین در حالت باینری، دنباله شمارش به صورت ۰۰۰، ۰۰۱، ۰۱۰، ۰۱۱، ۱۰۰، ۱۰۱ خواهد بود. حال زمانی که شمارنده به مقدار ۱۱۰ (۶) برسد، گیت منطقی ترکیبی، این حالت را تشخیص میدهد و یک خروجی سطح ۱ منطقی را ایجاد میکند.
از خروجی سطح HIGH گیت ترکیبی میتوان استفاده کرد تا شمارنده را پس از رسیدن به مقدار شمارش ۵ دسیمال، به حالت ۰ ریست شود. مدار شمارنده یک MOD-6 و شکل موجهای آن در تصویر زیر نشان داده شده است. زمانی که خروجی گیتهای منطقی ترکیبی، در سطح LOW منطقی قرار داشته باشند، هیچ تاثیری بر روی دنباله شمارش ندارند.
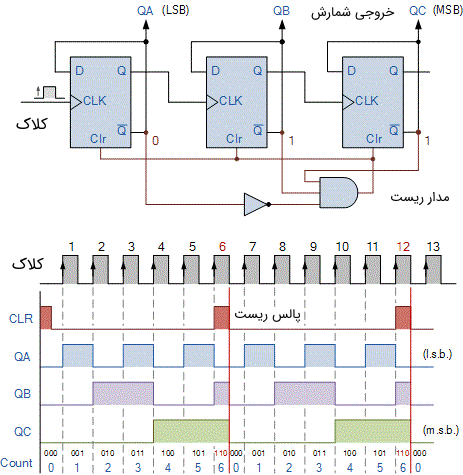
بنابراین میتوانیم از گیتهای منطقی ترکیبی در مدار یک شمارنده پایه (سنکرون یا آسنکرون) استفاده کنیم تا هر شمارنده MOD دلخواهی را ایجاد کنیم. توسط این گیتهای منطقی، میتوان هر یک از حالتهای شمارش را دیکود کرد و با استفاده از خروجی گیت منطقی، شمارنده را در آن حالت مورد نظر ریست کرد. در مثال ساده بالا، از یک گیت AND سه ورودی برای دیکود کردن حالت 110 استفاده کردیم. اولین باری که هر دو خروجی $$ Q_B $$ و $$ Q_C $$ با هم یک میشوند، زمانی است که شمارنده عدد ۶ را میشمارد. بنابراین، این دو خروجی بدون استفاده از گیت NOT مستقیما به پایههای گیت AND اعمال میشوند. اما خروجی $$ Q_A $$ ابتدا به گیت NOT وارد شده و سپس به گیت AND اعمال میشود.
یکی از معایب استفاده از شمارنده آسنکرون برای تولید شمارنده MOD با دنباله شمارش دلخواه، اثر نامطلوب گلیچ (Glitches) است. این اثر هنگام رسیدن شمارنده به مقدار ریست رخ میدهد. در این زمان بسیار کوتاه، خروجیهای شمارنده ممکن است یک حالت نادرست اتخاذ کنند. بنابراین بهتر است که از شمارنده سنکرون به جای شمارنده آسنکرون برای ایجاد شمارنده MOD بهره بگیریم. زیرا در شمارنده سنکرون تمام فلیپ فلاپها در یک زمان و توسط یک پالس ساعت کلاک میشوند، بنابراین در یک زمان و با هم تغییر حالت میدهند.
شمارنده MOD-10
یک مثال بسیار خوب از شمارنده MOD-m که از مدار ترکیبی خارجی برای تولید یک شمارنده MOD-10 استفاده میکند، شمارنده ده دهی است. شمارنده ده دهی (مقسم بر ۱۰) مانند TTL 74LS90 دارای ده حالت در دنباله شمارش خود است و در نمایشگرهای ارقام به عنوان رابط کاربری بسیار کاربرد دارد.
شمارنده ده دهی دارای ۴ خروجی است و میتواند اعداد ۴ بیتی باینری تولید کند. همچنین با استفاده از گیتهای AND و OR میتوان وقوع شمارش ۹ را تشخیص داد و شمارنده را به مقدار ۰ ریست کرد. همانند سایر شمارندههای MOD، این شمارنده نیز پالسهای کلاک را یکی پس از دیگری دریافت میکند و از ۰ تا ۹ شمارش را انجام میدهد.
زمانی که شمارش به ۹ دسیمال برسد، شمارنده به جای اینکه ۱۰ دسیمال یا ۱۰۱۰ باینری را بشمارد، به مقدار ۰ ریست میشود. مدار پایه یک شمارنده ده دهی را میتوان با استفاده از فلیپ فلاپهای JK ساخت. این فلیپ فلاپها در لبههای منفی یا پایین رونده پالس کلاک تغییر حالت میدهند. نمایی از یک شمارنده ده دهی MOD-10 در تصویر زیر نشان داده شده است.
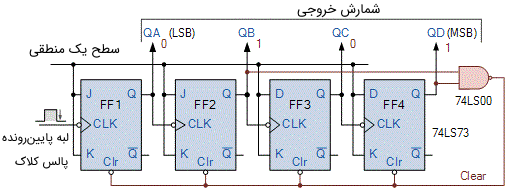
خلاصه شمارندههای MOD
در این مقاله به بررسی شمارندههای MOD پرداختیم. شمارندههای MOD یا شمارندههای باینری، مدارات ترتیبی هستند که یک دنباله باینری از بیتها را در پاسخ به پالس کلاک تولید میکنند و حالت شمارنده باینری توسط ترکیب تمام خروجیهای آن تعیین میشود.
تعداد حالتهای خروجی متفاوتی که یک شمارنده میتواند تولید کند، پیمانه یا Modulus آن شمارنده نام دارد. پیمانه یا MOD هر شمارنده برابر با مجموع حالتهای یکتایی است که یک شمارنده در طی یک چرخه کامل شمارش طی میکند. یک شمارنده MOD_n را همچنین یک شمارنده مقسم بر n میگویند.
پیمانه یک شمارنده بر اساس رابطه $$2^n $$ محاسبه میشود که در آن n برابر با تعداد فلیپ فلاپهای مدار شمارنده است. بنابراین یک شمارنده با ۳ فلیپ فلاپ توان شمارش ۸ حالت مختلف را دارد و یک شمارنده MOD-8 نام دارد. بیشینه عددی که توسط یک شمارنده باینری شمارش میشود برابر با $$ 2^n -1 $$ است. یک شمارنده MOD-8 میتواند در حالت باینری از ۰۰۰ تا ۱۱۱ بشمارد، یعنی بیشینه عددی که شمارنده میتواند بشمارد برابر با هفت ($$ 2^3 -1 $$) است.
میتوان با استفاده از مدارات ترکیبی خارجی، شمارندههای MOD رایج که دارای MODهایی برابر با ۲، ۴، ۸ و سایر اعداد توان دو هستند را به نحوی پیکربندی کرد که تا یک عدد خاص شمارش را انجام دهند. به عبارت دیگر، قبل از رسیدن به بیشینه عدد قابل شمارش توسط شمارنده، ریست شوند.
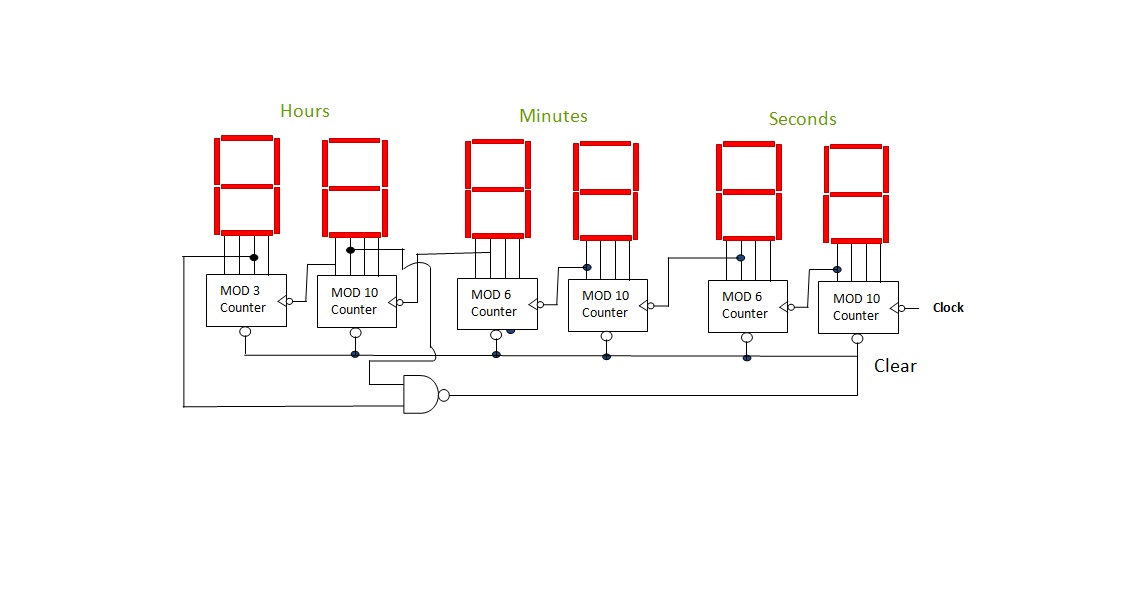
یکی از متداولترین شمارندههای MOD-m با دنباله شمارش منقطع، شمارنده ده دهی است که یک شمارنده MOD-10 محسوب میشود. این شمارنده دارای ده حالت شمارش مختلف است، در حالی که میتواند ۱۶ حالت شمارشی مختلف داشته باشد. به عبارت دیگر این شمارنده از ۰ تا ۹ شمارش را انجام میدهد، در حالی که قادر است دنباله شمارشی از ۰ تا ۱۵ داشته باشد. سایر شمارندههای MOD عبارتند از شمارندههای MOD-6 و MOD-3 که در ساعتهای دیجیتالی برای نمایش اوقات روز مورد استفاده قرار میگیرند.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مدارهای منطقی (طراحی دیجیتال)
- مجموعه آموزشهای نرمافزارهای مهندسی برق و الکترونیک
- آموزش مدار منطقی (مرور – تست کنکور ارشد)
- منطق دیجیتال — از صفر تا صد
- آموزش سیستمهای باینری — مجموعه مقالات جامع وبلاگ فرادرس
- شیفت رجیستر — از صفر تا صد
^^