شمارنده آسنکرون — راهنمای جامع (+ دانلود فیلم آموزش رایگان)
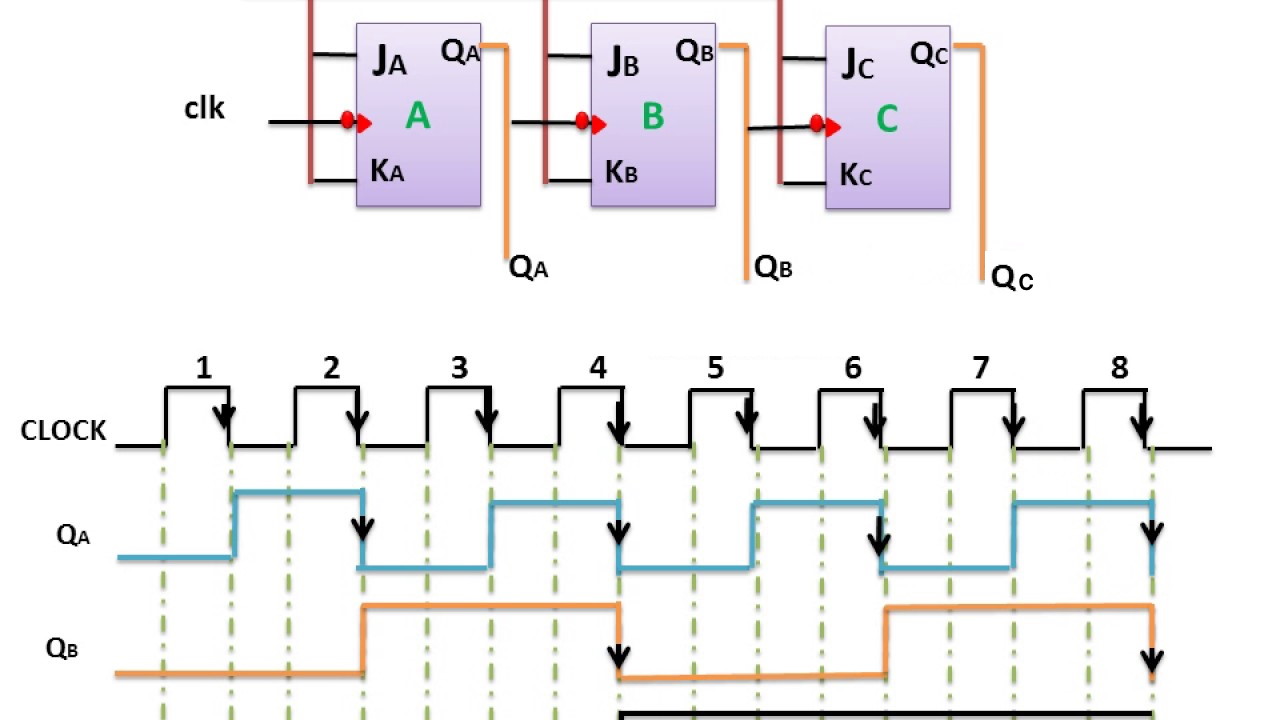
شمارنده آسنکرون (Asynchronous Counter) از فلیپ فلاپهایی که به صورت سری به یکدیگر متصل شدهاند، بهره میگیرد تا بتواند پالس کلاک ورودی را به صورت موجی در طول شمارنده حرکت دهد. در این مطلب به بیان اصول کاری شمارندههای آسنکرون میپردازیم.
فیلم آموزشی شمارنده آسنکرون
یک شمارنده آسنکرون میتواند $$2^n -1 $$ حالت شمارش محتمل داشته باشد. به عبارت دیگر MOD 16 برای یک شمارنده ۴ بیتی (از ۰ تا ۱۵)، آن را برای کاربردهای مقسم فرکانسی بسیار ایدهآل میسازد. همچنین میتوان از آرایش شمارنده آسنکرون پایه برای ساخت شمارندههای مخصوصی بهره برد که در آنها حالتهای شمارش از بیشینه شماره خروجی کمتر هستند. شمارندههای MOD نمونهای از چنین شمارندههایی محسوب میشوند. این نوع مدارات به این صورت ایجاد میشوند که شمارنده باید خود را در مقادیر از پیش تعیین شده، به صفر ریست کند. در نتیجه نوعی از شمارندههای آسنکرون ایجاد میشوند که دارای دنباله منقطع (Truncated Sequence) هستند.
بنابراین یک شمارنده n بیتی که تا بیشینه MOD خود ($$2^n $$) میشمارد، یک شمارنده دنباله کامل (Full Sequence) نام دارد. به همین ترتیب میتوان گفت که یک شمارنده n بیتی که MOD آن کمتر از بیشینه ممکن است، یک شمارنده منقطع محسوب میشود.
اما ممکن است این سوال پیش بیاید که چرا میخواهیم یک شمارنده آسنکرون منقطع بسازیم که در آن MOD برابر با اعداد ۴ یا ۸ (یا سایر اعدادی که توان کامل ۲ باشند.) نیست. در جواب به این سوال میتوان گفت که با استفاده از مدارات منطقی ترکیبی در ورودیهای آسنکرون فلیپ فلاپها، میتوان از مزایای آنها استفاده کرد.
شمارنده آسنکرون ده دهی
اگر یک شمارنده آسنکرون با MOD ۱۶ را انتخاب کنیم و آن را با گیتهای منطقی اضافی اصلاح کنیم، میتوانیم به خروجی شمارنده دهدهی (مدار مقسم بر ده) دست یابیم و از آن در شمارندههای دسیمال استاندارد و مدارات حسابی (Arithmetic) استفاده کنیم.
این شمارندهها معمولا تحت عنوان شمارندههای ده دهی (Decade Counter) شناخته میشوند. در یک شمارنده ده دهی نیاز است تا زمانی که شمارش به ضرایب ده برسد، خروجی به مقدار صفر ریست شود. به عبارت دیگر خروجی باید برابر با DCBA=1010 باشد. برای رسیدن به این هدف، باید وقوع این حالت را به ورودی ریست مدار فیدبک دهیم. یک شمارنده با رشته شمارش از 0000 باینری (BCD = 0) تا 1001 (BCD=9)، شمارنده BCD یا شمارنده دسیمال کد باینری (Binary Coded Decimal) نامیده میشود؛ زیرا دنباله ده حالتی خروجی آن همان کد BCD است. اما شمارندههای ده دهی باینری بسیار متداولتر هستند.
در شکل زیر نمایی از نحوه اتصال فلیپ فلاپها به منظور تشکیل یک شمارنده ده دهی دیده میشود.
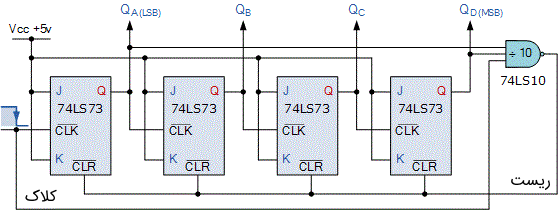
این نوع از شمارندههای آسنکرون، در هر لبه پالس کلاک به سمت بالا شمارش میکنند. شمارش از ۰۰۰۰ شروع میشود تا به 1001 (۹ دسیمال) برسد. حال هر دو خروجی $$ Q_A $$ و $$ Q_D $$ برابر با منطق یک هستند. با ورود پالس کلاک بعدی، خروجی گیت NAND 74LS10 وضعیت را از یک منطقی به صفر منطقی تغییر میدهد.
از آنجا که خروجی گیت NAND به ورودی CLEAR تمام فلیپ فلاپهای JK متصل شده است، این سیگنال تمام خروجیهای Q را مجبور میکند تا به حالت منطقی 0000 ریست شوند. حال خروجیهای $$ Q_A $$ و $$ Q_B $$ هر دو در سطح صفر منطقی هستند و فلیپ فلاپ تازه ریست شده است. در این زمان خروجی گیت NAND مجددا به حالت یک منطقی باز میگردد، بنابراین شمارنده دوباره شمارش را از ۰۰۰۰ شروع میکند. در نتیجه با استفاده از چنین مداری شمارنده ده دهی به سادگی ساخته میشود.
جدول درستی این شمارنده در زیر آورده شده است.
| مقدار دسیمال | $$ Q_A $$ | $$ Q_B $$ | $$ Q_C $$ | $$ Q_D $$ | شماره کلاک |
| 0 | 0 | 0 | 0 | 0 | 1 |
| ۱ | 1 | 0 | 0 | 0 | ۲ |
| ۲ | 0 | 1 | 0 | 0 | ۳ |
| ۳ | 1 | 1 | 0 | 0 | ۴ |
| ۴ | 0 | 0 | 1 | 0 | ۵ |
| ۵ | 1 | 0 | 1 | 0 | ۶ |
| ۶ | 0 | 1 | 1 | 0 | ۷ |
| ۷ | 1 | 1 | 1 | 0 | ۸ |
| ۸ | 0 | 0 | 0 | 1 | ۹ |
| ۹ | 1 | 0 | 0 | 1 | ۱۰ |
| شمارنده خروجی خود را به مقدار صفر ریست میکند. | ۱۱ | ||||
با استفاده از ایده مدار بالا به سادگی میتوان مدارهای دیگری را ایجاد کرد که برای چرخههای شمارش دیگری نیز مناسب باشند. برای این کار میتوان اتصالات ورودیهای گیت NAND را تغییر داد و یا از ترکیبات دیگری از گیتهای منطقی استفاده کرد.
به عنوان مثال یک شمارنده دوازده تایی (MOD=12) را میتوان به سادگی ایجاد کرد. کافی است ورودیهای گیت NAND را از خروجیهای $$ Q_C $$ و $$ Q_D $$ بگیریم. به یاد داشته باشید که معادل باینری عدد ۱۲ برابر است با ۱۱۰۰ و همچنین خروجی $$ Q_A $$ کم ارزشترین بیت (LSB) است.
از آنجا که بیشترین MOD که میتواند توسط n فلیپ فلاپ پیادهسازی شود برابر با $$2^n $$ است، هنگام طراحی یک شمارنده آسنکرون منقطع باید کمترین توان عدد ۲ را مشخص کرد که بزرگتر یا مساوی با MOD مورد نظر باشد. مثلا اگر بخواهیم که مدار از صفر تا ۳۹ بشمارد، در این صورت MOD برابر با ۴۰ است. بنابراین بیشترین تعداد فلیپ فلاپهای مورد نیاز شش عدد خواهد بود. این شش فلیپ فلاپ بیشینه MOD برابر با ۶۴ را در اختیار قرار میدهند. به همین دلیل مثلا ۵ فلیپ فلاپ کافی نیستند؛ چون مقدار MOD برابر با ۳۲ را فراهم میکنند.
حال فرض کنید که میخواهیم یک شمارنده مقسم بر ۱۲۸ را برای مقسم فرکانسی بسازیم. در این صورت به تعداد ۷ فلیپ فلاپ احتیاج خواهیم داشت که به صورت آبشاری به یکدیگر متصل شده باشند؛ زیرا $$2^7 = 128 $$ است. با استفاده از یک فلیپ فلاپ دوتایی مانند 74LS74، باز هم به چهار آی سی فلیپ فلاپ احتیاج داریم تا مدار را کامل کنیم.
روش جایگزین ساده دیگر این است که از دو آیسی TTL 7493 به عنوان مقسم/شمارنده موجی ۴ بیتی استفاده کنیم. از آنجا که $$ 128 =8 \times 16 $$ است، یک آیسی 7493 میتواند به عنوان یک مقسم بر ۱۶ و آیسی دیگر نیز یک مقسم بر ۸ مورد استفاده قرار گیرد. این دو آیسی برای تشکیل یک مقسم فرکانسی مانند شکل زیر به صورت آبشاری به یکدیگر متصل میشوند.
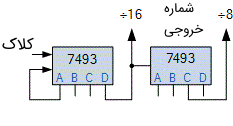
البته آیسیهای آسنکرون استاندارد مانند TTL 74LS90 نیز وجود دارند که مقسم/شمارنده موجی قابل برنامهریزی هستند و میتوانند به صورت مقسم بر ۵ و یا مقسم بر ۲ و یا ترکیبی از هر دو مورد استفاده قرار گیرند. این آیسی بسیار انعطافپذیر بوده و دارای ترکیبات متنوعی مانند مقسم بر ۲، ۴، ۵، ۱۰، ۲۰، ۲۵، ۵۰ و حتی ۱۰۰ نیز هست.
مقسم فرکانسی
این توانایی شمارندههای موجی که میتوانند دنبالههای منقطع را بشمارند و یک خروجی تقسم شده بر n را تولید کنند، شمارندهها و مخصوصا شمارندههای موجی را برای کاربردهای مقسم فرکانسی بسیار کارا میکند. در واقع با این ادوات میتوان فرکانس ورودی بسیار بالای پالس کلاک را به مقدار پایینتری تبدیل کرد تا در کلاکهای دیجیتال و کاربردهای زمانبندی بیشتر قابل استفاده باشند. برای مثال فرض کنید دقیقا به سیگنال زمانبندی با فرکانس ۱ هرتز برای عملکرد یک کلاک دیجیتال نیاز داریم. میتوان به سادگی یک پالس موج مربعی یک هرتزی را با آیسی تایمر ۵۵۵ که در آرایش مولتی ویبراتور آستابل باشد، تولید کرد، اما طبق دیتا شیت کارخانه سازنده آیسی، میتوان به این نکته پی برد که هر آیسی بسته به کارخانه تولید کننده حدود ۱ تا ۲ درصد خطای زمانبندی دارد. حال برای فرکانس پایین مورد نیاز ما، یعنی فرکانس یک هرتز، این مقدار خطای ۲ درصدی به هیچ وجه قابل صرف نظر نیست.
علاوه بر این، دیتا شیت هر آیسی مقدار بیشینه فرکانس عملکرد تایمر ۵۵۵ مربوطه را نیز به کاربر میدهد. به عنوان مثال در اکثر آیسیها این فرکانس در حدود ۳۰۰ کیلو هرتز است. در این فرکانس بزرگ نیز مقدار خطای ۲ درصد، باعث ایجاد خطای ۶ کیلو هرتزی در فرکانس تولید شده توسط تایمر ۵۵۵ میشود. اما این مقدار تقریبا قابل قبول است. پس با انتخاب یک فرکانس زمانبندی بزرگتر مانند ۲۶۲٫۱۴۴ کیلو هرتز و یک شمارنده موجی ۱۸ بیتی، میتوان سیگنال زمانبندی دقیق با فرکانس یک هرتز ساخت. نمایی از این مدار در شکل زیر نشان داده شده است.

هر چند مثال بالا، یک مدار بسیار ساده از نحوه تولید فرکانس دقیق زمانبندی را نشان میدهد، اما با استفاده از یک کریستال نوسانساز با فرکانس بالا و یک مقسم فرکانسی چند بیتی، میتوان یک مولد فرکانسی بسیار دقیق را ایجاد کرد. چنین مولدهای فرکانسی برای بازه بسیار وسیعی از کاربردها از ساعتها تا المانهای زمانبندی وقایع و حتی پیانوهای الکتریکی یا سایر ادوات موسیقی مورد استفاده قرار میگیرند.
متاسفانه یکی از بزرگترین معایب شمارندههای آسنکرون این است که یک تاخیر بسیار کوچک بین دریافت پالس ساعت در ورودی مربوطه و حاضر شدن این پالس در خروجی وجود دارد که دلیل آن مدارات داخلی گیتها است.
در مدارات آسنکرون این تاخیر با نام تاخیر انتشاری (Propagation Delay) شناخته میشود و به همین دلیل به شمارندههای موجی آسنکرون گاهی شمارندههای انتشاری نیز میگویند و در مواردی که فرکانس بسیار بالا باشد، این انتشار میتواند منجر به تولید دنباله شمارش اشتباه در خروجی شود.
در مدارات شمارنده موجی با تعداد بیتهای زیاد، اگر تاخیر طبقات مختلف همگی با یکدیگر جمع شوند، در نتیجه مجموع تاخیر در انتهای زنجیره شمارنده را میتوان به دست آورد که برابر با اختلاف زمانی بین سیگنال ورودی و سیگنال خروجی شمارنده است و نسبتا مقدار بزرگی دارد. دقیقا به همین دلیل است که شمارندههای آسنکرون معمولا در مدارات شمارنده فرکانس بالا که شامل تعداد بیتهای زیادی هستند، مورد استفاده قرار نمیگیرند.
خروجیهای شمارنده، رابطه زمانی ثابتی با یکدیگر ندارند و به دلیل دنباله پالسهای کلاکی، هر کدام در یک لحظه ثابت زمانی اتفاق نمیافتند. به عبارت دیگر، فرکانسهای خروجی یکی پس از دیگری ظاهر میشوند و به نوعی مانند اثر دومینو هستند. بنابراین هر چه تعداد فلیپ فلاپهای بیشتری به شمارنده آسنکرون افزوده شود، بیشترین فرکانس کاری کمتر میشود تا شمارش دقیقتری فراهم شود. لازم به ذکر است که برای غلبه بر مشکل تاخیر انتشار در شمارندههای آسنکرون، شمارندههای سنکرون به وجود آمدند.
خلاصه
حال اگر بخواهیم مزایای شمارندههای آسنکرون را به صورت خلاصه بار دیگر بیان کنیم، میتوانیم به موارد زیر اشاره کنیم:
- شمارندههای آسنکرون میتوانند به سادگی از فلیپ فلاپهای نوع D یا نوع JK ساخته شوند.
- این شمارندهها به این دلیل آسنکرون نامیده میشوند که در آنها ورودی کلاک مربوط به فلیپ فلاپها توسط یک پالس کلاک یکسان عمل نمیکنند.
- هر خروجی در دنباله به یک تغییر در حالت در خروجی فلیپ فلاپ قبلی بستگی دارد.
- شمارنده آسنکرون گاهی شمارنده موجی نیز نامیده میشود؛ زیرا این طور به نظر میرسد که دادهها در خروجی یک فلیپ فلاپ به ورودی فلیپ فلاپ دیگر به صورت موجی حرکت میکنند.
- این شمارندهها میتوانند توسط مدارات شمارنده تقسیمکننده بر n نیز پیاده سازی شوند.
- شمارندههای منقطع میتوانند با هر عدد MOD دلخواه به صورت عملی پیادهسازی شوند.
از معایب شمارنده آسنکرون نیز میتوان به موارد زیر اشاره کرد:
- ممکن است به یک فلیپ فلاپ خروجی سنکرون کننده اضافی احتیاج باشد.
- برای شمارش دنباله منقطعی که برابر با $$ 2^n $$ نباشد، به یک فیدبک اضافی منطقی هم نیاز است.
- برای شمارش تعداد بیتهای زیاد، تاخیر انتشار توسط طبقات متوالی ممکن است به صورت ناخواسته مقدار بسیار بزرگی باشد.
- به دلیل وجود این تاخیر در مدار، گاهی به شمارندههای آسنکرون، شمارنده انتشاری نیز میگویند.
- خطای شمارش درکلاکهای فرکانس بالا اتفاق میافتد.
- شمارندههای سنکرون به دلیل این که برای تمام فلیپ فلاپها از یک سیگنال کلاک یکسان استفاده میکنند، بسیار قابل اعتمادتر و نیز سریعتر هستند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مدارهای منطقی (طراحی دیجیتال)
- مجموعه آموزشهای نرمافزارهای مهندسی برق و الکترونیک
- آموزش مدار منطقی (مرور – تست کنکور ارشد)
- منطق دیجیتال — از صفر تا صد
- آموزش سیستمهای باینری — مجموعه مقالات جامع وبلاگ فرادرس
- شیفت رجیستر — از صفر تا صد
^^










