سطح مقطع هیدرولیکی در کانال باز – به زبان ساده

پیشتر در مجله فرادرس، در مقاله جریان در کانال باز، انواع رژیم جریان، انرژی مخصوص و پایستگی جرم و انرژی را بررسی کردیم. سیستمهای کانال باز، عموماً برای انتقال مایع به محلی که در ارتفاع پایینتری قرار دارد، مورد استفاده قرار میگیرند. همچنین برای به حداقل رساندن هزینهها از تأثیر نیروی گرانش به عنوان نیروی محرکه جریان استفاده میشود. به این ترتیب، نیازی به هیچگونه انرژی ورودی نیست و فقط در مرحله ساخت اولیه، هزینه صرف میشود. از این رو، برای طول واحدی از یک کانال، محیط کانال در بحث هزینه تمام شده، تعیین کننده خواهد بود. بنابراین، با مینیمم کردن این پارامتر میتوان هزینهها را کاهش داد. در این مقاله، انواع سطح مقطع هیدرولیکی در کانال باز را مورد بررسی قرار داده و بهینهترین مقادیر را به دست خواهیم آورد.
از سوی دیگر، مقاومت در برابر جریان، ناشی از تنش برشی دیواره $$\large \tau_w$$ و مساحت دیواره بوده که به نوعی با محیط تر شونده در واحد طول کانال، معادل است. بنابراین، اگر سطح مقطع جریان $$\large A_c$$ ثابت باشد، با کوچکتر شدن محیط تر شونده $$\large p$$، نیروی مقاومتی نیز کاهش مییابد. در مقابل، سرعت متوسط و دبی جریان افزایش خواهند یافت. به عبارت دیگر، اگر هندسه کانال، شیب $$\large S_0$$ و نوع پوشش سطحی کانال (که معرف ضریب سختی $$\large n$$ است) مشخص باشد، سرعت جریان با استفاده از رابطه مانینگ قابل محاسبه است.
$$\large V \:=\: a R ^ { \frac {2} {3} } _ h S ^ { \frac {1} {2 } } _ 0 / n$$
با توجه به این رابطه، سرعت جریان با افزایش شعاع هیدرولیکی، بالا میرود. به همین دلیل، برای به حداکثر رساندن سرعت متوسط جریان یا نرخ دبی حجمی در واحد سطح مقطع جریان باید شعاع هیدرولیکی ماکسیمم شود (یعنی با توجه به رابطه $$\large R_h \: = \: A_c / p$$ محیط تر شونده باید به کمترین مقدار خود برسد). بنابراین، میتوانیم عبارت زیر را نتیجهگیری کنیم:
«اگر سطح مقطع جریان در کانال باز مشخص باشد، بهترین سطح مقطع هیدرولیکی، هنگامی پدید میآید که شعاع هیدرولیکی ماکسیمم شود و یا به عبارت دیگر، محیط تر شونده به مقدار حداقل برسد.»
شکلی که نسبت محیط به مساحت آن مینیمم باشد، دایره است. در نتیجه، براساس مقاومت جریان مینیمم، بهترین سطح مقطع برای جریان در کانال باز، یک نیمدایره خواهد بود. شکل زیر را در نظر بگیرید. ساختن یک کانال با دیوارههای صاف، هزینههای کمتری به دنبال دارد. بدین منظور باید به جای سطح مقطع نیمدایره از اشکال هندسی مستطیل یا ذوزنقه استفاده کرد. در ادامه، به آنالیز هریک از این اشکال هندسی خواهیم پرداخت تا بهترین سطح مقطع هیدرولیکی را بیابیم.
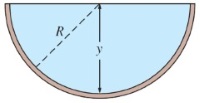
انواع سطح مقطع هیدرولیکی
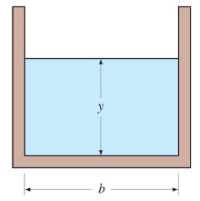
در ابتدا کانالی را با سطح مقطع مستطیلی مطابق شکل زیر در نظر بگیرید. جنس دیوارههای این کانال از بتن پرداخت شده ($$\large n \: = \: 0.012$$) با عرض $$\large b$$ و عمق جریان $$\large y$$ است و سطح زیرین کانال، $$\large 1$$ درجه شیب دارد. فرض کنید سطح مقطع جریان $$\large 1 \: m^ 2$$ باشد.
برای تعیین تأثیرات نسبت ابعادی $$\large \frac { y } {b }$$ روی شعاع هیدرولیکی $$\large R_ h$$ و نرخ دبی حجمی جریان $$\large \dot { V}$$، با کمک رابطه مانینگ مقادیر $$\large R_ h$$ و $$\large \dot { V}$$ محاسبه شده است.
نتایج به دست آمده را در نمودار زیر مشاهده میکنید. این نمودار برای نسبتهای ابعادی $$\large 0.1$$ تا $$\large 5$$ رسم شده است. همانطور که مشاهده میکنید، با افزایش نسبت ابعادی جریان، دبی حجمی $$\large \dot { V }$$ نیز زیاد میشود. این روند ادامه مییابد تا اینکه در نقطه $$\large \frac { y } {b } \: = \: 0.5$$ دبی به بیشترین میزان خود میرسد. از این نقطه به بعد، دبی رو به کاهش میرود (از آنجایی که سطح مقطع جریان برابر واحد است، دبی حجمی برابر با سرعت جریان نیز خواهد بود). با توجه به این دادهها میتوان نتیجه گرفت که شعاع هیدرولیکی هم همین روند را طی میکند. اما همه چیز برای محیط تر شوندگی متفاوت است و عکس این روند را به دنبال خواهد داشت. این نتایج تأیید میکند که بهترین سطح مقطع هیدرولیکی در بیشترین شعاع هیدرولیکی رخ میدهد. به بیان دیگر، میتوان گفت در این حالت شعاعِ تر شونده به کمترین مقدار خود میرسد.
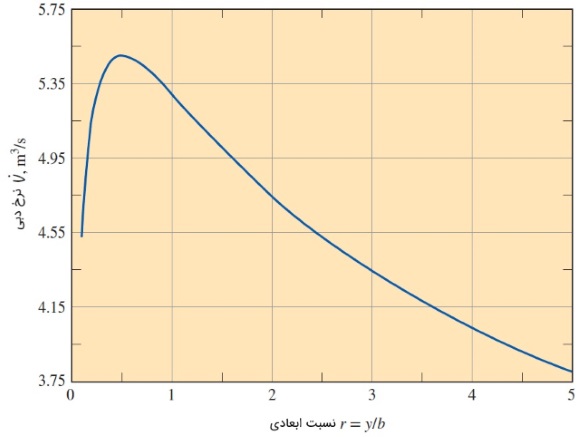
سطح مقطع هیدرولیکی در کانال مستطیلی
جریان مایع در کانال باز با سطح مقطع مستطیلی را در نظر بگیرید. عرض و عمق جریان به ترتیب برابر $$\large b$$ و $$\large y$$ است. سطح مقطع و محیط تر شونده جریان با رابطههای زیر تعیین میشوند.
$$\large A_c \: = \: y b \\ ~ \\
\large p \: = \: b \: + \: 2 y$$
با ادغام این دو رابطه، میتوانیم محیط را برحسب مساحت بنویسیم.
$$\large p \: = \: \frac {A_c } { y}\: + \: 2 y$$
طبق تعریفی که در قسمت قبل ارائه کردیم، در صورت ثابت بودن سطح مقطع جریان، بهترین سطح مقطع هیدرولیکی در کانال باز با کوچکترین محیط تر شونده متناظر است. به همین منظور، در رابطه بالا با فرض ثابت بودن $$\large A_c$$، از $$\large p$$ نسبت به $$\large y$$ مشتق میگیریم.
$$\large \frac{\text {d} p }{\text {d} y } \: = \: - \: \frac {A_c} {y ^2} \: + \: 2 \: = \: - \: \frac {b y} {y ^ 2} \: + \: 2 \: = \: - \: \frac {b} {y} \: + \: 2$$
اگر رابطه بالا را مساوی صفر قرار داده و نسبت به $$\large y$$ حل کنیم، شرط لازم و کافی برای بهترین سطح مقطع هیدرولیکی در کانال مستطیلی به صورت زیر به دست میآید.
$$\large \Rightarrow ~~~ y \: = \: \frac { b } { 2 }$$
به عبارت دیگر، برای اینکه در کانال مستطیلی، مقاومت جریان به حداقل و نرخ دبی حجمی به حداکثر مقدار خود برسد، کافی است ارتفاع مایع نصف عرض کانال باشد. در این حالت، محیط تر شونده و در نتیجه، هزینه ساخت کانال نیز به کمترین مقدار خود خواهد رسید.
سطح مقطع هیدرولیکی در کانال ذوزنقهای
در عمل، بسیاری از کانالهای ساخته شده به دست انسان، مستطیلی یا دایرهای نیستند. بلکه با سطح مقطع ذوزنقهای ساخته میشوند. مطابق شکل زیر، جریان مایع در کانال باز با سطح مقطع ذوزنقهای را در نظر بگیرید.
عرض پایین این کانال $$\large b$$، عمق جریان $$\large y$$ و زاویه ذوزنقه آن $$\large \theta$$ است. سطح مقطع جریان و محیط تر شونده را میتوانیم با کمک رابطههای زیر به دست آوریم.
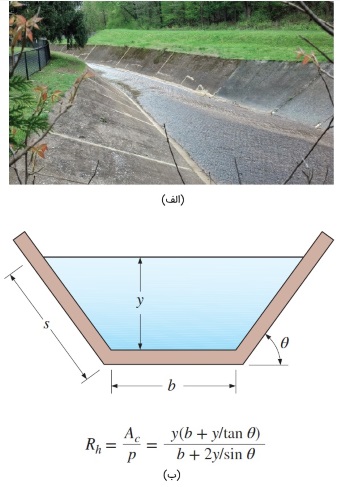
$$\large A_c \: = \: (b \: + \: \frac { y } { \tan \theta }) y \\ ~ \\
\large p \: = \: b \: + \: \frac { 2 y } { \sin \theta }$$
با یک جابجایی کوچک و ادغام دو رابطه بالا، میتوانیم محیط تر شونده را برحسب سطح مقطع جریان بازنویسی کنیم.
$$\large p \: = \: \frac {A_c } { y } \: - \: \frac { y } {\tan \theta} \: + \: \frac { 2 y } {\sin \theta}$$
برای پیدا کردن مقطعی از نمودار که در آن محیط تر شونده به مینیمم مقدار خود میرسد، باید از رابطه بالا نسبت به $$\large y$$ مشتق گرفته و مقدار $$\large A_c$$ را نیز ثابت فرض کنیم.
$$\large \frac{ \text {d} p } { \text {d} y } \: = \: - \: \frac {A_c } {y ^ 2 } \: - \: \frac { 1 } { \tan \theta} \: + \: \frac { 2 } { \sin \theta } \: = \: - \: \frac {b \: + \: y / \tan \theta} { y } \: - \: \frac { 1 } { \tan \theta } \: + \: \frac { 2 } {\sin \theta}$$
اکنون، رابطه بالا را مساوی صفر قرار داده و نسبت به $$\large y$$ حل کنیم. بهترین سطح مقطع هیدرولیکی در کانال ذوزنقهای به صورت زیر نتیجه میشود.
$$\large y \: = \: \frac { b \sin \theta } { 2 ( 1 \: - \: \cos \theta ) }$$
(رابطه ۱)
در حالتی که زاویه ذوزنقه، قائم باشد، رابطه بالا به رابطه $$\large y \: = \: \frac { b } { 2 }$$ تبدیل میشود. شعاع هیدرولیکی یک کانال با سطح مقطع ذوزنقهای را میتوان به صورت زیر محاسبه کرد.
$$\large R _ h \: = \: \frac { A_c } { p } \: = \: \frac { y (b \: + \: y / \tan \theta) } { b \: + \: 2 y / \sin \theta} \: = \: \frac {y ( b \sin \theta \: + \: y \cos \theta) } { b \sin \theta \: + \: 2 y}$$
(رابطه ۲)
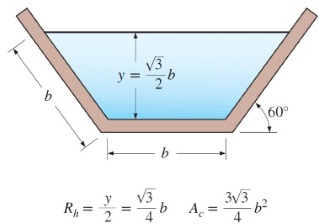
با مقایسه رابطههای شماره ۱ و ۲، شعاع هیدرولیکی برای کانال ذوزنقهای و بهترین سطح مقطع هیدرولیکی برابر $$\large R _ h \: = \: \frac { y } { 2 }$$ به دست میآید. بنابراین، شعاع هیدرولیکی در کانال ذوزنقهای با بهترین سطح مقطع هیدرولیکی مستقل از زاویه $$\large \theta$$ و برابر با نصف عمق جریان است. به طور مشابه، به منظور یافتن زاویه ذوزنقه برای بهترین سطح مقطع هیدرولیکی مشتق $$\large p$$ را نسبت به $$\large \theta$$ محاسبه میکنیم. در اینجا، $$\large A_c$$ و $$\large y$$ ثابت هستند. با قرار دادن مشتق $$\large p$$ برابر صفر و حل آن برحسب زاویه $$\large \theta$$، بهینهترین زاویه ذوزنقهای برابر $$\large \theta \: = \: 60 ^ \circ$$ به دست میآید. با جایگذاری این زاویه در رابطه شماره ۱، بهینهترین عمق جریان برای این زاویه به صورت زیر محاسبه میشود.
$$\large y \: = \: \frac { \sqrt {3} } { 2 } b$$
به این ترتیب، طول لبه جانبی مقطع جریان و سطح مقطع جریان به شیوه زیر به دست میآید.
$$\large s \: = \: \frac { y } { \sin 60 ^ \circ } \: = \: \frac {b \: \sqrt {3} / 2 } { \sqrt {3} / 2 } \: = \: b \\ ~ \\
\large p \: = \: 3 b \\ ~ \\
\large A_c \: = \: ( b \: + \: \frac { y } { \tan \theta } ) y \: = \: ( b \: + \: \frac {b \sqrt {3} / 2 } {\tan 60 ^ \circ} ) ( b \sqrt {3} / 2 ) \: = \: \frac {3 \sqrt { 3 }} {4} b ^ 2$$
میتوان نتیجه گرفت که بهترین سطح مقطع هیدرولیکی برای کانال ذوزنقهای، نصف یک ششضلعی منتظم است. زیرا یک ششضلعی منتظم، شباهت زیادی به دایره دارد و در بین تمام کانالهای ذوزنقهای، کمترین محیط تر شونده به ازای سطح مقطع ثابت، در نیم ششضلعی منتظم اتفاق میافتد. شکل زیر را در نظر بگیرید.
مثال: بهترین سطح مقطع هیدرولیکی در کانال باز
سؤال: در یک کانال باز، آب با نرخ دبی حجمی $$\large 2 \: m ^ 3$$ به صورت یکنواخت جریان دارد. پوشش سطحی این کانال از آسفالت و شیب کف آن برابر $$\large 0.001$$ است. ابعاد سطح مقطع هیدرولیکی بهینه را برای کانال الف) مستطیلی، ب) ذوزنقهای به دست آورید. ضریب مانینگ برای کانال باز با پوشش دیواره از جنس آسفالت، $$\large 0.016$$ است.
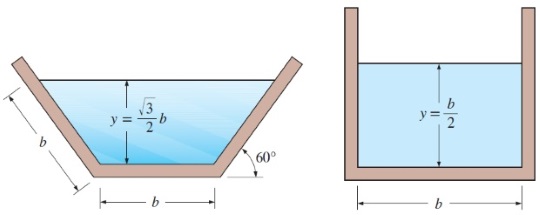
پاسخ: الف) برای رسیدن به بهترین سطح مقطع هیدرولیکی برای کانال مستطیلی، ارتفاع جریان باید برابر با نصف عرض کانال باشد. در این حالت، سطح مقطع جریان، محیط تر شونده و شعاع هیدرولیکی به صورت زیر محاسبه میشود.
$$\large y \: = \: b / 2 \\ ~ \\
\large A_c \: = \: b y \: = \: \frac {b ^ 2} {2} \\ ~ \\
\large p \: = \: b \: + \: 2 y \: = \: 2 b \\ ~ \\
\large R_h \: = \: \frac { A_c } { p } \: = \: \frac { b} { 4 }$$
با جایگذاری رابطههای بالا در معادله مانینگ، حل مسأله را ادامه میدهیم.
$$\large \dot { V } \: = \: \frac { a } { n } A_c {R_h} ^ {2 / 3} {S_0} ^ {1 / 2} \\ ~ \\
\large b \: = \: ( \frac {2 n \dot { V } 4 ^ {2 / 3} } { a \sqrt { S_ 0 } } ) ^ {3 / 8 } \: = \: ( \frac {2 (0.016) (2 \: m ^ 3 / s ) 4^ {2 / 3} } { (1 \: m ^ {1 / 3 } / s ) \sqrt {0.001} } ) ^ {3 / 8 } \\ ~ \\
\large b \: = \: 1.84 \: m$$
بنابراین، سطح مقطع و محیط تر شونده به ترتیب برابر $$\large A_c \: = \: 1.70 \: m ^ 2$$ و $$\large p \: = \: 3.68 \: m$$ به دست میآیند و ابعاد سطح مقطع هیدرولیکی بهینه به قرار زیر است.
$$\large b \: = \: 1.84 \: m ~~ ~~ ~~ ~~ y \: = \: 0.92 \: m$$
ب) برای رسیدن به بهترین سطح مقطع هیدرولیکی برای کانال ذوزنقهای، زاویه ذوزنقه باید برابر $$\large 60^ \circ$$ و ارتفاع جریان نیز برابر $$\large y\: =\: b\: \sqrt{ 3} /2$$ باشد. در این حالت، سطح مقطع جریان، محیط تر شونده و شعاع هیدرولیکی به شکل زیر خواهند بود.
$$ \large A_c\: =\: y(b \:+ \:b \cos \theta) \:= \:0.5 \sqrt{ 3} b^ 2( 1\: +\: \cos 60^ \circ )\: =\: 0.75 \sqrt{3 }b ^2 \\ ~\\
\large p\: =\: 3b \\ ~\\
\large R_h \:=\: \frac {y} {2} \:= \frac {\sqrt {3 }} {4 }b $$
در ادامه، این مقادیر را در رابطه مانینگ جایگذاری میکنیم.
$$\large \dot { V } \: = \: \frac { a } { n } A_c {R_h} ^ {2 / 3} {S_0} ^ {1 / 2} \\ ~ \\
\large b \: = \: ( \frac {(0.016) (2 \: m ^ 3 / s )} {0.75 \sqrt{3} (\sqrt{3} /4) ^{2/3} (1 \: m ^ {1 / 3 } / s ) \sqrt {0.001} } ) ^ {3 / 8 } \\ ~ \\
\large b \: = \: 1.12 \: m$$
بنابراین، سطح مقطع و محیط تر شونده به ترتیب برابر $$\large A_c \: = \: 1.64 \: m ^ 2$$ و $$\large p \: = \: 3.37 \: m$$ محاسبه میشوند و ابعاد سطح مقطع هیدرولیکی بهینه به ترتیب زیر است.
$$\large b \: = \: 1.12 \: m ~~ ~~ ~~ y \: = \: 0.973 \: m ~~ ~~ ~~ \theta \: = \: 60 \: ^\circ$$
همانطور که مشاهده کردید کانال با سطح مقطع ذوزنقهای بهتر است؛ زیرا محیط آن کوچکتر بوده ($$\large 3.37 \: m$$ در مقایسه با $$\large 3.68 \: m$$) و در نتیجه هزینه ساخت آن نیز کمتر خواهد شد. به همین دلیل است که بیشتر کانالهای مصنوعی با سطح مقطع ذوزنقهای ساخته میشوند. البته به دلیل کوچکتر شدن مقدار $$\large A_c$$ در این کانالها، سرعت متوسط جریان بیشتر خواهد بود.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک و شاخه سیالات، آموزشهای زیر نیز پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مکانیک
- مجموعه آموزشهای دروس مهندسی مکانیک
- آموزش هیدرولیک برای مهندسین عمران
- تابع پتانسیل و جریان پتانسیل در سیالات — از صفر تا صد
- فلومتر (Flowmeter) – از صفر تا صد
- ورتکس (Vortex) چیست؟ — به زبان ساده
- جریان در کانال باز – از صفر تا صد
^^









