فرادرستوربین فرانسیس (Francis Turbine) – از صفر تا صد
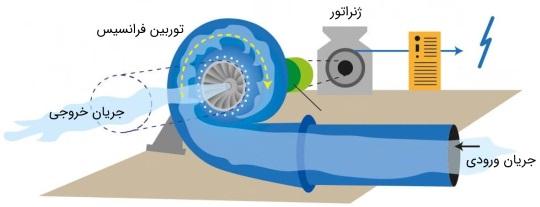
تولید توان، همیشه یکی از موضوعات چالش برانگیز صنعت بوده است. روش‌های امروزی با وجود پیشرفت‌های زیاد، هنوز هم انرژی و سوخت زیادی را مصرف می‌کنند. مصرف انرژی و جمعیت، همواره در حال افزایش است. در نتیجه، بدیهی است که مهندسان در پی روش‌های طبیعی و کم هزینه باشند. استفاده از ویژگی‌های فیزیکی آب و رفتار آن در طبیعت، می‌تواند یکی از راه‌های چاره باشد. توان هیدروالکتریکی یکی از روش‌هایی است که با وجود دوستی با طبیعت، می‌تواند نیاز به انرژی را تا حد زیادی تأمین کند. یکی از این راه‌ها استفاده از توربین است. همان‌طور که قبلاً در مقاله توربوماشین (Turbomachinery) — به زبان ساده از مجله فرادرس گفتیم، توربین انرژی جنبشی را از سیال کاری (مثلاً آب) گرفته و محور متصل به ژنراتور را به حرکت در می‌آورد. کوپل شدن توربین و یک ژنراتور را به صورت شماتیک در شکل زیر مشاهده می‌کنید. در این مقاله به بررسی توربین فرانسیس به عنوان یکی از پرمصرف‌ترین انواع توربین‌ها می‌پردازیم.
تاریخچه توربین فرانسیس
در حال حاضر، رایج‌ترین و محبوب‌ترین توربین در صنعت، توربین فرانسیس است. این توربین، از انواع عکس‌العملی به حساب می‌آید. تحقیقات روی توربین‌های عکس‌العملی از زمان «لئونارد اویلر» (Leonhard Euler) دانشمند سوئیسی در دهه 1750 میلادی آغاز شده بود.
تا قبل از سال 1838، اصلاحات زیادی روی آن انجام شد. ولی در این سال «جیمز فرانسیس» (James B. Francis) مهندسی که اصلیتی انگلیسی-آمریکایی داشت، تغییراتی در ساختار این توربین اعمال کرد. فرانسیس، پره‌های راهنمای ثابت را اضافه کرد و شکل پره‌ها را طوری طراحی کرد تا آب بتواند با زاویه درست و بدون شوک (shock free)، وارد آنها شود. امروزه توربین فرانسیس در هِد (head)های متوسط و زیاد، بیشترین کاربرد را دارد.
بخش‌های توربین فرانسیس
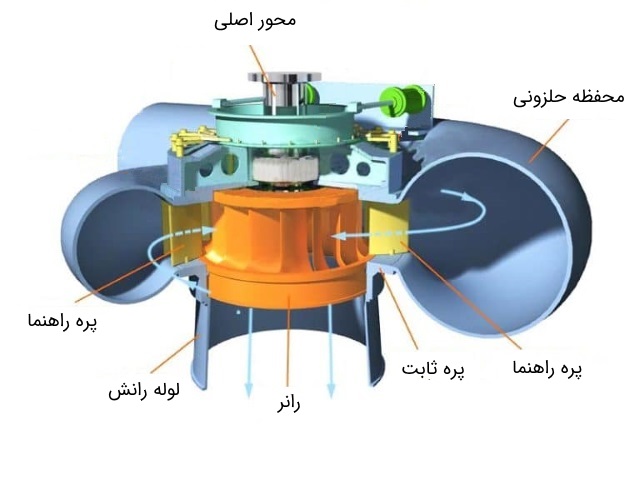
بیشتر توربین‌های فرانسیس طوری ساخته می‌شوند که محورشان عمودی قرار بگیرد. برخی توربین‌های کوچکتر می‌توانند محورهای افقی هم داشته باشند. در شرایطی که محدودیتی برای اندازه وجود نداشته باشد، توربین عمودی انتخاب اول است. شکل زیر، قسمت‌های مختلف توربین فرانسیس را نشان می‌دهد. شکل پره‌ها در توربین فرانسیس طوری است که می‌تواند به صورت همزمان از انرژی جنبشی و پتانسیل سیال برای تولید توان استفاده کند. در نتیجه، دیگر نگرانی برای افت هد وجود نخواهد داشت. در این قسمت، بخش‌های اصلی توربین فرانسیس را تشریح می‌کنیم.
محفظه حلزونی
محفظه حلزونی (spiral casing) که به عنوان غلاف حلزونی هم شناخته می‌شود، محلی برای ورود آب است. آب مخزن یا آب سد، از طریق همین مسیر و با فشار زیاد وارد توربین می‌شود. پره‌های توربین به صورت دایره‌ای قرار گرفته‌اند. بنابراین، آبی که قرار است به پره‌های توربین ضربه بزند، باید برای راندمان بهتر، در جهت چرخشی جریان پیدا کند. بدین منظور از محفظه حلزونی استفاده شده است. البته باید این موضوع را در نظر داشت که حرکت چرخشی موجب تلف شدن بخشی از فشار می‌شود. والوت (volute) و اسکرول (scroll) نام‌های دیگری است که به جای محفظه حلزونی به کار می‌روند.
پره‌های ثابت
پره‌های ثابت و راهنما، آب را به سمت پره‌های رانِر هدایت می‌کنند. وظیفه اصلی آنها این است که بخشی از انرژی پتانسیل سیال را در ورودی به انرژی جنبشی تبدیل کنند و سپس سیال را با زاویه دلخواه به سمت پره‌های رانر روانه سازند. پره‌های ثابت (stay vanes) در موقعیت خود ثابت می‌مانند و چرخش آب را که از جریان شعاعی ناشی شده، کاهش می‌دهد. در این حالت، راندمان توربین بالاتر می‌رود.
پره‌های راهنما
پره‌های راهنما (guide vanes) ثابت نیستند و با توجه به نیازمندی‌های مربوط به کنترل زاویه برخورد آب به پره‌های توربین، می‌توان زاویه آنها را تغییر داد. با این کار، راندمان هم بالا می‌رود. پره‌های راهنما، به عنوان دریچه‌های هادی (wicket gates) هم شناخته می‌شوند. از سوی دیگر، نرخ دبی آب هم به سمت پره‌های رانِر تنظیم می‌شود تا توان خروجی با توجه به بار توربین، قابل کنترل باشد.
پره‌های رانِر
عملکرد و راندمان توربین تا حد زیادی به چگونگی طراحی پره های رانِر (runner blades) وابسته است. در یک توربین فرانسیس، پره‌های رانر به دو بخش تقسیم می‌شوند. نیمه پایینی به شکل یک سطل کوچک ساخته می‌شود تا از نیروی ضربه آب برای چرخاندن توربین استفاده کند. اما نیمه بالایی از نیروی عکس‌العمل آب بهره می‌برد. این دو نیرو در کنار هم، موجب چرخیدن توربین می‌شوند. هنگام عبور آب از پره‌های رانر، از مومنتوم زاویه‌ای آب کاسته شده و روی محور توربین کار انجام می‌شود. در شرایط طراحی، جریان در راستای محوری از رانر خارج می‌شود. در شکل زیر، نمایی از پره‌های رانر در توربین فرانسیس را مشاهده می‌کنید. رانر در توربین فرانسیس معمولاً از حدود ۱۶ تا ۲۴ پره منحنی تشکیل می‌شود. جنس رانر برای هد کم، از چدن ریخته‌گری و برای هِدهای زیاد از آلیاژ فولاد انتخاب می‌شود. قطر رانر را می‌توان حداکثر تا ۷ متر هم طراحی کرد.
لوله رانش
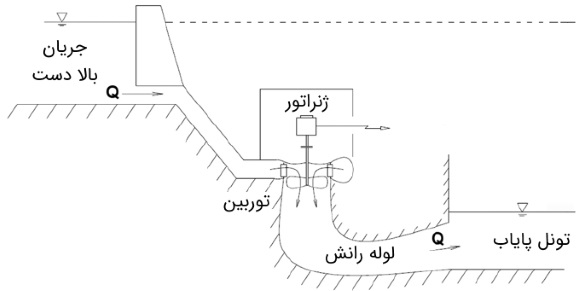
در حالت کلی، فشار در خروجی رانر در توربین‌های عکس‌العملی، کمتر از فشار اتمسفر است. در نتیجه، آب نمی‌تواند مستقیماً در تونل پایاب (tail race) تخلیه شود. بدین منظور باید از لوله‌ای استفاده شود که سطح مقطعش آرام آرام افزایش می‌یابد. از این لوله برای تخلیه آب از نقطه خروجی توربین تا تونل پایاب استفاده می‌شود. این لوله، لوله رانش (draft tube) نام دارد که در برخی مقاله‌های فارسی، مانند نام انگلیسی آن، «درفت تیوب» هم خوانده می‌شود. یک سرِ لوله رانش به خروجی رانر وصل است و انتهای دیگرش درون تونل پایاب و پایین‌تر از سطح آب، مستغرق می‌شود. این کار، همچنین کمک می‌کند تا همیشه داخل توربین پر از آب باشد. در شکل زیر، محل نصب لوله رانش را به صورت شماتیک، مشاهده می‌کنید.
عملکرد توربین فرانسیس
همان‌طور که در بخش قبل گفتیم، آب از طریق محفظه حلزونی توربین، به سمت پره‌های ثابت و راهنما روانه می‌شود. قطر محفظه حلزونی، آرام آرام کم می‌شود تا قدری از افت فشار جریان جبران شود. اکنون آب به پره‌های ثابت می‌رسد. پره‌های ثابت، موجب می‌شوند تا چرخش از حرکت آب حذف شود و جریان آب، رفتار خطی و مستقیم پیدا کند. خطی بودن جریان آب، در مرحله بعد به کمک پره‌های راهنما خواهد آمد. زیرا منحرف کردن جریان خطی توسط این پره‌ها راحت‌تر انجام می‌گیرد. زاویه پره‌های راهنما، زاویه حمله را در پره‌های رانر تعیین می‌کند. از طرف دیگر، پره‌های رانر هم ثابتند و زاویه آنها قابل تغییر نیست. در نتیجه، با تنظیم پره‌های راهنما، می‌توان خروجی توان توربین را کنترل کرد. حداکثر توان خروجی توربین فرانسیس می‌تواند به $$\large 350 \: MW$$ برسد.
شکل زیر، مسیر حرکت آب در بین پره‌های رانر توربین فرانسیس (شکل الف) و مثلث سرعت (شکل ب) را در محل ورودی و خروجی آن نشان می‌دهد. در محل ورود به پره‌های راهنما، جریان در صفحه شعاعی-مماسی است. سرعت پره‌ها در ورود به پره‌های راهنما با $$\large c_1$$ و زاویه جریان با $$\large \alpha_1$$ نشان داده شده است. سرعت $$\large c_1$$ در صفحه شعاعی-مماسی قرار دارد و می‌توان آن را به دو مؤلفه شعاعی $$\large c_{r 1}$$ و مماسی $$\large c_{\theta 1}$$ تقسیم کرد. در این حالت، رابطه زیر بین این دو مؤلفه برقرار است.
$$\large \tan \alpha = \frac {c_{\theta 1}} {c_{r 1}}$$
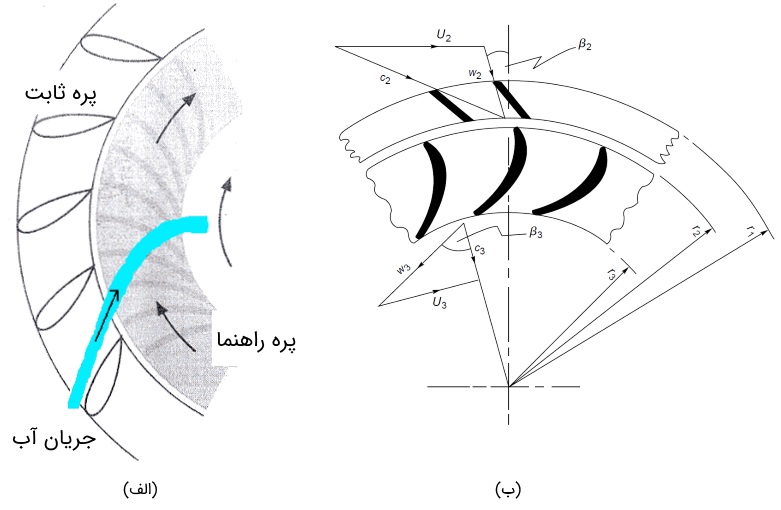
در هنگام ورود جریان به رانر، سرعت آن $$\large c_2$$ و زاویه آن $$\large \alpha _2$$ خواهد بود. در این حالت، سرعت جریان نسبت به پره رانر را به صورت $$\large w_2 = c_2 - U_2$$ تعریف می‌کنیم. $$\large U_2$$ سرعت پره است. حال با توجه به شکل، زاویه $$\large \beta_2$$ برابر با عبارت زیر خواهد بود.
$$\large \tan \beta_2 = \frac {c_{\theta 2} - U_2} {c_{r2}}$$
با کمی دقت در تصاویر در می‌یابیم که بردار سرعت جریانی که به پره‌های راهنما و رانر می‌رسد، در هر دو نقطه، با خطوط انحنا در هر ردیف مماس است. ایده‌آل‌ترین وضعیت برای اینکه جریان ورودی، با افت کم و بدون شوک باشد، همین حالت است. به همین دلیل، در تمام مسائل مرتبط با جهت جریان، زاویه جریان از اهمیت بالایی برخوردار است.
سرعت نسبی جریان و زاویه آن در خروج از رانر به ترتیب با $$\large w_3$$ و $$\large \beta _3$$ نشان داده شده است. زاویه $$\large \beta _3$$ را می‌توان به صورت زیر به دست آورد. در اینجا فرض می‌شود هنوز مقداری از سرعت چرخشی $$\large c_{\theta 3}$$ باقیمانده است. در بیشتر تحلیل‌ها، برای سادگی از این مقدار صرف نظر می‌شود.
$$\large \tan \beta _3 = \frac {c_{\theta 3} + U_3} {c_{r3}}$$
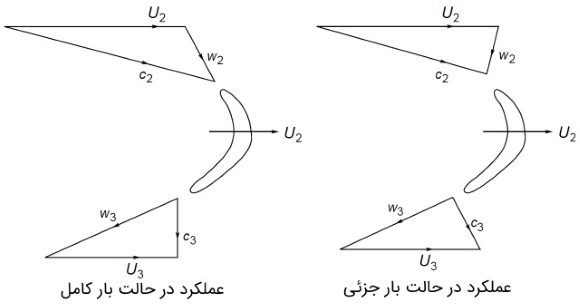
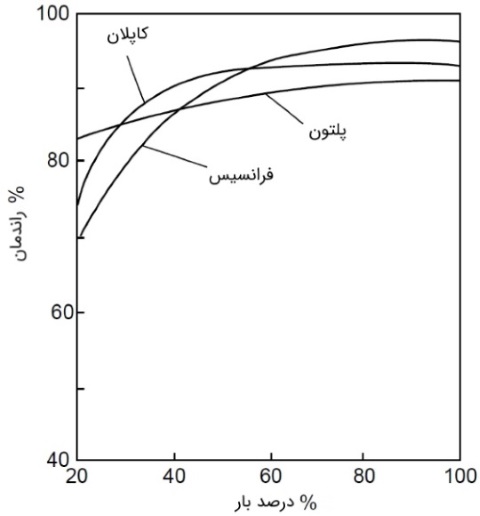
هنگامی که قرار است توربین فرانسیس با بار جزئی کار کند، با تنظیم زاویه پره‌های راهنما می‌توان جریان را محدود کرد. در این حالت، توان خروجی $$\large Q$$ کاهش می‌یابد ولی سرعت پره‌ها هنوز ثابت است. شکل بالا، مثلث سرعت را در دو حالت بار کامل و بار جزئی نشان می‌دهد. شکل زیر هم مقایسه راندمان هیدرولیکی توربین فرانسیس را با دو توربین دیگر و برحسب درصدهای مختلف بار نشان می‌دهد. در این نمودار، سرعت و هد، ثابت فرض شده است.
معادلات پایه در توربین فرانسیس
معادله توربین اویلر بین دو نقطه ۲ و ۳ را می‌توانیم به صورت زیر بنویسیم.
$$\large \Delta W = U_2c_{\theta 2} - U_3c_{\theta 3}$$
اگر فرض کنیم جریان در خروجی رانر هیچ‌گونه چرخشی نداشته باشد، می‌توان $$\large U_3c_{\theta 3}$$ را در رابطه بالا برابر صفر در نظر گرفت. هد مؤثر برای تمام توربین‌های عکس‌العملی برابر $$\large H_E$$ است و به صورت کل هد در دسترس در ورودی توربین نسبت به سطح تونل پایاب تعریف می‌شود. انرژی در ورودی رانر را می‌توان برابر با مجموع انرژی‌های جنبشی، پتانسیل و فشار نوشت.
$$\large g(H_E - \Delta H_N) = \frac {p_2 - p_a}{\rho} + \frac {1} {2} c^2_2 + gz_2$$
عبارت $$\large \Delta H_N$$ نشان دهنده افت هد و ناشی از اصطکاک در محفظه حلزونی و پره‌های راهنما است. فشار استاتیک مطلق در ورودی را با $$\large p_2$$ نشان داده‌ایم. در خروجی رانر، انرژی آب به دلیل میزان کار مخصوص $$\large \Delta W$$ و کار اصطکاک در رانر $$\large g\Delta H_R$$، باز هم کاهش می‌یابد. این انرژی باقیمانده برابر با مجموع انرژی‌های پتانسیل فشار و جنبشی و به صورت زیر است.
$$\large g(h_E - \Delta H_N - \Delta H_R) - \Delta W = \frac {1} {2} c^2_3 + \frac {p_3} {\rho}\: - \frac {p_a} {\rho} \: +gz_3$$
فشار استاتیک مطلق در خروجی رانر را با $$\large p_3$$ نشان داده‌ایم. با مقایسه دو رابطه اخیر، به نتیجه زیر می‌رسیم. در این رابطه، $$\large p_{02}$$ و $$\large p_{03}$$ به ترتیب، فشار کل مطلق در ورودی و خروجی رانر هستند.
$$\large \Delta W = \frac {p_{02} \: - p_{03} } {\rho} \: - \: g \Delta H_R \: + g(z_2 - \: z_3)$$
شکل زیر، لوله رانش را متصل به یک توربین فرانسیس با محور عمودی نشان می‌دهد. مهمترین بُعد نشان داده شده در این شکل، فاصله عمودی ($$\large z = z_3$$) بین صفحه خروج از رانر و سطح آزاد تونل پایاب است. حال می‌توانیم معادله انرژی بین محل خروج از رانر و تونل پایاب را به صورت زیر بنویسیم.
$$\large \frac {p_3} {\rho} \: + \: \frac {1} {2} c^2_3 \: + \: gz_3 \: - \: g \Delta H_{DT} \: = \: \frac {1} {2} c^2_4 \: + \: \frac {p_a} {\rho}$$
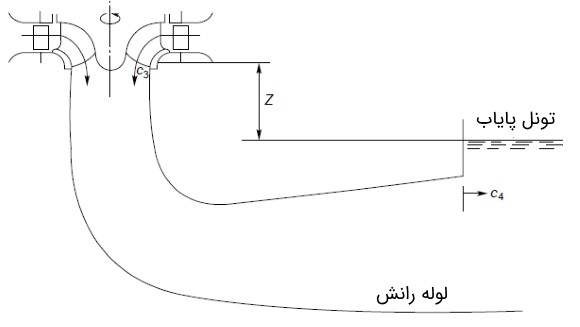
در رابطه بالا، $$\large \Delta H_{DT}$$ و $$\large c_4$$ به ترتیب، افت هد در لوله رانش و سرعت جریان خروجی را نشان می‌دهند. یکی دیگر از پارامترهای مهم در توربین‌های هیدرولیک، راندمان هیدرولیک است که به شیوه زیر تعریف می‌شود.
$$\large \eta_h = \frac {\Delta W} {g H_E} = \frac {U_2c_{\theta 2} - U_3c_{\theta 3}} {gH_E}$$
همان‌طور که پیش‌تر گفتیم، اگر فرآیند را ایده‌آل فرض کنیم، جریان در خروج از رانر هیچ‌گونه حرکت چرخشی ندارد و رابطه $$\large c_{\theta 3} = 0$$ برقرار است. در این حالت و با جایگذاری این مقدار، راندمان هیدرولیکی به شکل زیر ساده می‌شود.
$$\large \eta_h = \frac {U_2c_{\theta 2} } {gH_E}$$
راندمان کل را به صورت $$\large \eta_o = \eta _m \times \eta _h$$ تعریف می‌کنیم. توان توربین‌های نسبتاً بزرگ، تقریباً در بازه $$\large 500 \: -1000\: W$$ قرار می‌گیرد. برای این توربین‌ها، افت‌های مکانیکی ناچیز است و راندمان مکانیکی را می‌توان %$$\large 100$$ فرض کرد. در این حالت، راندمان کل با راندمان هیدرولیکی برابر می‌شود.
نسبت سرعت نوک پره به سرعت جت آب را با $$\large v = \frac {U_2} {c_1}$$ نشان می‌دهیم. برای رسیدن به عملکرد بهینه در توربین پلتون (Pelton)، مقدار این نسبت بسیار بحرانی است. ولی در توربین فرانسیس، می توان این نسبت را در دامنه نسبتاً وسیعی به صورت $$\large 0.6 \leq v \leq 0.95$$ نگه داشت. در بیشتر موارد، توربین فرانسیس برای به حرکت در آوردن یک ژنراتور سنکرون به کار می‌رود. در این حالت، سرعت‌های چرخشی با توجه به مقادیر ۵۰ یا ۶۰ دور در هر ثانیه (هرتز) انتخاب می‌شود و سرعت باید ثابت بماند.
با تغییر زاویه پره‌های راهنما، توربین می‌تواند در شرایط بار جزئی کار کند. این تغییر زاویه به کمک یک مکانزیم چرخ دنده انجام می‌شود. باید به این نکته توجه داشت که عملکرد توربین تحت بار جزئی موجب می‌شود سرعت جریان پایین‌دست، چرخشی شده و راندمان روتور کاهش یابد. در نتیجه، جریان گردابه تشکیل خواهد شد. ممکن است این جریان گردابه به قدری قدرتمند باشد که بتواند باعث کاویتاسیون در طول محور لوله رانش شود.
مثال
سؤال: در یک توربین فرانسیس با محور عمودی، هد آب در فلنج ورودی، $$\large 150 \: m$$ است. فاصله عمودی بین رانر و تونل پایاب را برابر با $$\large 2 \: m$$ در نظر بگیرید. سرعت نوک رانر، $$\large 35 \: m/s$$ و سرعت شعاعی آب در ورود به رانر، $$\large 10.5 \: m/s$$ است. همچنین، حرکت آب در خروج از رانر بدون چرخش بوده و سرعت آب در هنگام خارج شدن از لوله رانش، $$\large 3.5 \: m/s$$ تخمین زده می‌شود. اگر افت‌های مختلف برابر مقادیر زیر باشند، موارد خواسته شده را به دست آورید.
$$\large \Delta H _N = 6.0 \: m , ~~~ \Delta H _R = 10.0 \: m , ~~~ \Delta H _{DT} = 1.0 \: m , ~~~$$
الف) کار مخصوص $$\large \Delta W$$ و راندمان هیدرولیکی $$\large \eta_h$$ در توربین؛
ب) سرعت مطلق $$\large c_2$$ در ورودی رانر؛
پ) هد فشار (نسبت به تونل پایاب) در ورودی و خروجی رانر؛
ت) زاویه مطلق و نسبی جریان در ورودی رانر.
پاسخ: الف) کار مخصوص و راندمان هیدرولیکی را می‌توان به راحتی و به طریق زیر محاسبه کرد.
$$\large \Delta W = g\: (H_E \: - \Delta H_N \: - \Delta H_R \: - \Delta H_{DT}) \: - \frac {1} {2} c^2_4 \\~\\
\large = 9.81 \times (150 \:- 6 \:- 10 \:- 1) \: - \frac {3.5^2} {2} \:= 1298.6 \: \frac {m^2} {s^2} \\~\\
\large \eta_h = \frac {\Delta W} {g H_E} \: = 0.8825$$
ب) جریان خروجی، بدون سرعت چرخشی بوده و در نتیجه، رابطه $$\large c_{\theta 3} = 0$$ برقرار است. سرعت مطلق آب در ورودی رانر را به صورت زیر به دست می‌آوریم.
$$\large \Delta W = U_2 c_{\theta 2} ~~~ \Rightarrow ~~~ c_{\theta 2} = 37.1 \:m/s \\~\\
\large c_2 = \sqrt {c^2_{\theta 2} \: + c^2_{r2}} = \sqrt {37.1^2 \:+10.5^2} \:= \: 38.56 \: m/s$$
پ) هد فشار در ورودی و خروجی به شکل زیر قابل محاسبه است.
$$\large H_2 = H_E \: - \Delta H_N \: - \frac {c^2_2} {2g} \\~\\
\large H_2 = 150 \:- 6 \:- \frac {38.56 ^ 2} {2 \times 9.81} = 68.22 \:m \\~\\
\large H_3 = \frac {p_3 - p_a} {\rho g} = \frac {c^2_4 - c^2_3} {2g} \:+ \Delta H_{DT} \:- z_3 \\~\\
\large H_3 = \frac {3.5^2 - 10.5^2} {2 \times 9.81} \: = \: -6.0 \:m$$
به این نکته توجه کنید که علامت منفی برای $$\large H_3$$ نشان می‌دهد فشار در این نقطه کمتر از فشار اتمسفر است. این موضوع، یکی از مهمترین ملاحظاتی است که باید در طراحی و عملکرد توربین هیدرولیک مد نظر قرار گیرد.
ت) اکنون می‌توانیم زاویه‌های جریان را در ورودی رانر، به طریق زیر بیابیم.
$$\large \alpha_2 = \tan^{-1} (\frac {c_{\theta 2}} {c_{r2}}) \: = \tan^{-1} (\frac {37.1} {10.5}) = 74.2 ^ \circ \\~\\
\large \beta_2 = \tan^{-1} (\frac {c_{\theta 2} - U_2} {c_{r2}}) = \tan^{-1} (\frac {37.1 - 35} {10.5}) = 11.31 ^ \circ$$
در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک حرارت و سیالات، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس مهندسی مکانیک
- آموزش مکانیک سیالات
- مجموعه آموزش‌های مهندسی مکانیک
- آنتروپی — از صفر تا صد
- پرش هیدرولیکی – از صفر تا صد
- توربوماشین (Turbomachinery) — به زبان ساده
- سیکل ترمودینامیکی اتو (Otto Cycle) و موتور احتراق داخلی — یادگیری با مثال
^^
