تقسیم اعداد اعشاری — آموزش با مثال و به زبان ساده

همانطور که می‌دانید، چهار عمل اصلی روی اعداد به صورت «جمع»، «تفریق»، «ضرب» و «تقسیم» در نظر گرفته می‌شود و همگی آن‌ها عملگرهایی با دو پارامتر دارند. وقتی می‌خواهیم یک عدد را به بخش‌های مساوی تقسیم کنیم، عمل ریاضی مناسب، همان عملگر تقسیم است. به کمک تقسیم می‌توانیم مقداری را برحسب مقداری دیگر، به طور مساوی پخش کنیم. البته می‌دانید که عمل عکس تقسیم، به صورت ضرب شناخته می‌شود. در این نوشتار از مجله فرادرس در مورد تقسیم اعداد اعشاری که نوع خاصی از اعداد هستند صحبت خواهیم کرد.

قبل از خواندن این متن و شروع به اجرای تقسیم اعداد اعشاری در ریاضی، پیشنهاد می‌شود، به منظور آشنایی بیشتر با مجموعه اعداد صحیح و اعشاری، مطالب اعداد صحیح چیست و چه اعدادی هستند ؟ — به زبان ساده و اعداد اعشاری — به زبان ساده را مطالعه کنید. همچنین خواندن ضرب متقاطع یا طرفین و وسطین — به زبان ساده و اعداد گویا — به زبان ساده از مجله فرادرس نیز خالی از فایده نیست.

تقسیم اعداد اعشاری

به یاد دارید که در تقسیم، عددی که قرار است به بخش‌های مساوی تقسیم شود را مقسوم می‌نامیم. همچنین مقدار بخش‌ها برای تقسیم نیز مقسوم علیه نامیده شده و تعداد بخش‌ها حاصل از تقسیم نیز خارج قسمت گفته می‌شود.

اگر در انجام عمل تقسیم، مقداری باقی نمانده باشد و همه تقسیم‌ها کامل باشند، تقسیم بدون باقی‌مانده بوده به اصطلاح می‌گوییم باقی‌مانده تقسیم، صفر است و مقسوم به مقسوم علیه بخش‌پذیر است. ولی اگر بعد از محاسبه خارج قسمت، مقداری از عملیات تقسیم باقی مانده باشد، تقسیم به همراه باقی‌مانده نمایش داده می‌شود.

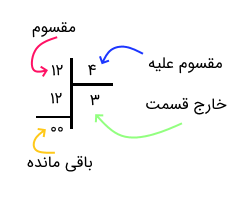
برای تقسیم اعداد اعشاری چند شیوه یا روش وجود دارد که در متن به آن‌ها اشاره خواهیم کرد. ابتدا حالت‌هایی را در نظر می‌گیریم که مقسوم یا مقسوم علیه، عدد طبیعی (صحیح) باشند. سپس با کمک نمایش اعشاری به صورت کسر، تقسیم را اجرا کرده و در انتها نیز عملیات تقسیم برای اعداد اعشاری را مرور می‌کنیم.

تقسیم اعداد اعشاری بر عدد صحیح

در تصویر بالا، بخش‌های یک تقسیم را بازگو کردیم. حال به وضعیتی در تقسیم می‌پردازیم که در آن، مقسوم یک عدد صحیح بوده و مقسوم علیه، یک عدد اعشاری است. برای این گونه تقسیم ابتدا از یک تکنیک تصویری کمک می‌گیریم، سپس محاسبه ریاضی را معرفی می‌کنیم.

مثال 1: خارج قسمت تقسیم ۰٫۰۹ بر ۳ چقدر است؟

راه حل: برای نمایش مقدار ۰٫۰۹ باید یک شکل را به ۱۰۰ بخش مساوی تقسیم کرده باشیم. برای مثال مربعی که در تصویر زیر دیده می‌شود، به ۱۰۰ بخش تقسیم شده و ۹ قسمت از آن به رنگ آبی درآمده تا نمایانگر ۰٫۰۹ باشد.

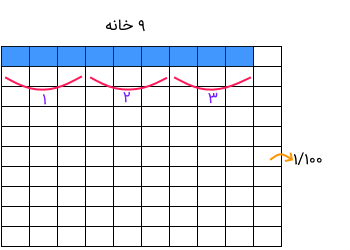
مشخص است که برای اجرای این تقسیم باید مساحت بخش آبی رنگ را به سه بخش یا قسمت، تفکیک کنیم. از آنجایی که ۹ خانه رنگی داریم، تقسیم آن‌ها به سه بخش مساوی، باعث ایجاد قسمت‌هایی خواهد شد که هر کدام سه خانه دارند. فقط توجه داشته باشید که هر یک از این خانه‌ها، نشانگر یک بخش از ۱۰۰ بخش هستند. بنابراین سه تا از این بخش‌ها، برابر با عدد ۰٫۰۳ خواهند بود. به این ترتیب نتیجه را به صورت زیر می‌نویسیم.

 ۰٫۰۹ ÷ ۳ = ۰٫۰۳

همین محاسبات را به شکل دیگری نیز می‌توان انجام داد. به این ترتیب درست به مانند روال معمول برای تقسیم اعداد صحیح عمل کرده و هر جایی در مقسوم، به علامت اعشار یا ممیز رسیدیم، در خارج قسمت هم ممیز خواهیم گذاشت. در مثال بعدی از این شیوه کمک گرفته‌ایم.

مثال ۲: می‌خواهیم عدد ۱۲٫۳۴ را بر ۲ تقسیم کنیم.

راه حل: همانطور که می‌بینید، مقسوم (۱۲٫۳۴) یک عدد اعشاری، و مقسوم علیه (۲) عدد صحیح است. مراحل را به مانند یک تقسیم معمولی انجام می‌دهیم.

• گام اول: از محل علامت ممیز مقسوم، یک خط عمودی تا انتهای عملیات تقسیم رسم می‌کنیم. این خط به ما یادآوری می‌کند که چه بخشی از محاسبات روی عدد اعشاری و چه بخشی روی اعداد صحیح انجام شده است. تقسیم بخش عدد صحیح از مقسوم بر مقسوم علیه را به شیوه معمول اجرا می‌کنیم. از آنجایی که تقسیم ۱۲ بر ۲، برابر است با ۶، در خارج قسمت، ۶ قرار داده و باقی‌مانده را محاسبه می‌کنیم. به تصویر زیر دقت کنید.

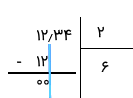
• گام دوم: از آنجایی که باقی‌مانده صفر شده یا بر ۲ بخش‌پذیر نیست (از ۲ کوچکتر است)، یک رقم دیگر از مقسوم را به پایین آورده و عمل تقسیم را بعد از ممیز آغاز می‌کنیم. این کار در تصویر زیر صورت گرفته است.

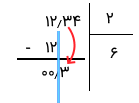
• گام سوم: از آنجایی که در گام قبلی رقم ۳ بعد از ممیز قرار گرفته، در خارج قسمت نیز ممیز قرار داده و عمل تقسیم را ادامه می‌دهیم.

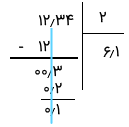
• گام چهارم: باز هم باقی‌مانده از مقسوم علیه کوچکتر شده و باید یک رقم از مقسوم اضافه کنیم. با اضافه کردن ۴ گام نهایی برداشته می‌شود.

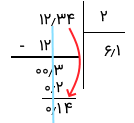
• گام پنجم: خارج قسمت تقسیم ۱۴ بر ۲ عدد ۷ خواهد بود. بنابراین ۷ را در ادامه رقم‌های مقسوم قرار می‌دهیم. باقی مانده تقسیم در اینجا برابر با صفر شده و هیچ رقمی از مقسوم باقی نمانده است. پس مراحل تقسیم تمام می‌شود. حاصل تقسیم ۱۲٫۳۴ بر ۲، مساوی با ۶٫۱۷ خواهد بود.

مثال ۳: حاصل تقسیم ۲۴٫۶ را بر ۱۲ مشخص کنید.

راه حل: شاید استفاده از تقسیم تفکیکی برای حل این مسئله تقسیم اعداد اعشاری در این حالت، ساده‌تر باشد. ابتدا ۲۴٫۶ را به صورت ۲۴ + ۰٫۶ می‌نویسیم، سپس تقسیم هر بخش را بر ۱۲ بدست می‌آوریم.

( ۲۴ + ۰٫۶ ) ÷ ۱۲ = ۲۴ ÷ ۱۲ + ۰٫۶ ÷ ۱۲ =

۲ + ۰٫۰۵ = ۲٫۰۵

مشخص است که برای تقسیم ۰٫۶ بر ۱۲ به همان روش قبلی عمل کرده‌ایم.

نکته: توجه داشته باشید که در تقسيم اعداد اعشاری بر عدد طبيعی یا صحیح، تعداد رقم‌های اعشار مقسوم، خارج قسمت و باقی‌مانده برابرند.

تقسیم عدد صحیح بر اعداد اعشاری

در این بخش از متن، حالت عکس بخش قبلی را برای تقسیم اعداد اعشاری مرور می‌کنیم. یعنی مقسوم علیه یک عدد اعشاری است ولی مقسوم، عدد صحیح است. قرار است تقسیم را برای این وضعیت با توجه به باقی‌مانده نیز مرور کنیم.

مثال 4: حاصل تقسیم ۲0 بر ۰٫۵ چیست؟

راه حل: یک شیوه جالب برای انجام این کار، رسم محور اعداد و تقسیم کردن واحد روی آن است. می‌دانید که منظور از عدد ۲0، مقداری است که از صفر به اندازه ۲0 واحد فاصله دارد. به شکل زیر دقت کنید.

در اینجا هم منظور از تقسیم ۲0 بر ۰٫۵، پیدا کردن تعدادی از اندازه‌های نیم واحدی (۰٫۵) است که ما را به ۲0 می‌رساند. با توجه به شکل زیر، تعداد 40 نیم واحد ما را به عدد ۲۰ خواهد رساند. پس تقسیم ۲۰ بر ۰٫۵ برابر با ۴۰ خواهد بود.

مثال 5: حاصل تقسیم ۲0 بر ۰٫۱ چقدر است؟

راه حل: همانطور که در مثال قبل دیدیم، باید هر واحد را به ۱۰ واحد تبدیل کنیم تا هر قسمت نشانگر ۰٫۱ باشد. پس اگر هر واحد را ۰٫۱ کنیم، فاصله ۲۰ تا صفر، ۱۰ برابر خواهد شد. به این ترتیب خواهیم فهمید که تقسیم ۲۰ بر ۰٫۱ برابر با ۲۰۰ خواهد بود.

۲۰ ÷ ۰٫۱ = ۲۰۰

می‌توان حاصل عمل تقسیم را به کمک ضرب هم امتحان کرد. کافی است خارج قسمت را در مقسوم علیه ضرب کرده و با باقی‌مانده جمع کنید. در مثال ما، ۰٫۱ مقسوم علیه و ۲۰۰ خارج قسمت بود. همچنین باقی‌مانده نیز صفر بدست آمد. پس به صورت زیر تقسیم را امتحان می‌کنیم.

۲۰۰ × ۰٫۱ + ۰= ۲۰

مثال 6: این بار عدد صحیح ۲5 را به ۰٫۸ تقسیم کنید.

راه حل: می‌دانیم این بار باید هر واحد را به اندازه ۰٫۸ در نظر بگیریم و از محور اعداد استفاده کنیم. ولی شاید راه ساده‌تر، استفاده از ضرب اعشاری باشد. می‌دانیم که ۱۰ در ۰٫۸ برابر با ۸ است. از طرفی ۲۰ در ۰٫۸ هم ۱۶ خواهد بود. به همین ترتیب عدد صحیح را افزایش می‌دهیم تا به مضربی از ۰٫۸ برسیم که نزدیک‌ترین مقدار به 25 بوده و از آن هم کوچکتر باشد. حتما به یاد دارید که باقی‌مانده تقسیم باید مثبت یا صفر باشد. به همین علت از بین مقادیر مضرب ۰٫۸ نزدیک‌ترین را انتخاب کرده‌ایم که از 25 کوچکتر باشد. مشخص است که ۳۱ مضربی است که حاصل ضرب آن در ۰٫۸ برابر با 24٫۸ است.

از همین جا خارج قسمت ۲۴٫۸ بدست آمده و باقی‌مانده هم برابر با ۰٫۲ خواهد بود زیرا فاصله بین این حاصل‌ضرب تا ۲۵ برابر با ۰٫۲ است.

همانطور که دیدید، در این مثال به کمک رابطه ضرب بین اعداد اعشاری، تقسیم را انجام دادیم.

نکته: اگر در يک تقسيم، مقسوم و مقسوم عليه را در عددی غير صفر ضرب كنيم، خارج قسمت تغييری نمی‌كند ولی باقی مانده هم در همان عدد ضرب می‌شود.

در قسمت‌های بعدی، حالتی از تقسیم اعداد اعشاری را معرفی می‌کنیم که به کمک آن، می‌توانید هر دو حالت قبلی را هم اجرا کنید. توجه دارید که باید نتیجه بدست آمده از روش‌های بعدی با روش‌های قبلی یکسان باشد. تفاوت فقط در شیوه انجام تقسیم یا طولانی بودن محاسبات است. استفاده از روش‌های بعدی، ساده‌تر و سریع‌تر بوده ولی در آن‌ها از مفاهیم ضرب کردن که در قبل در باره تقسیم اعداد اعشاری اشاره کردیم، استفاده شده است. به همین دلیل بهتر است هر دو مسیر را بدانید.

تقسیم اعداد اعشاری به کمک کسر

یکی از روش‌های ساده و راحت برای تقسیم اعداد اعشاری در ریاضی، تبدیل آن‌ها به صورت کسری است. به این ترتیب از همان شیوه تقسیم کسرها استفاده می‌کنیم. برای تقسیم کسرها، از قوانینی که در زیر فهرست شده‌اند، استفاده می‌کنیم.

برای تقسیم کسرها با مخرج یکسان، فقط صورت‌ها را بر هم تقسیم می‌کنیم.

مثال 7: اگر مقسوم سه چهارم و مقسوم علیه یک چهارم باشد، حاصل تقسیم چه خواهد بود.

راه حل: واضح است که باید تقسیم زیر صورت گیرد.

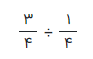
به توجه به توضیحی که داده شد، از آنجایی که مخرج‌ها در مقسوم و مقسوم علیه، با هم برابر هستند، کافی است صورت‌های کسرها را بر هم تقسیم کنیم. از آنجایی که صورت کسر اول (مقسوم) برابر با ۳ و صورت مقسوم علیه نیز برابر با ۱ است، حاصل تقسیم ۳ بر ۱ نیز، عدد ۳ خواهد بود.

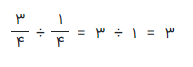
مثال 8: حاصل تقسیم عدد مخلوط را به صورت زیر معرفی می‌کنیم. قرار است تقسیم زیر را بسازیم.

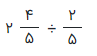
راه حل: لازم است ابتدا مقسوم را به صورت کسر متعارفی درآوریم، سپس عملیات تقسیم را به مانند قبل اجرا کنیم. به محاسبات زیر توجه کنید.

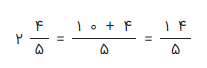
پس حاصل تقسیم به شکل زیر صورت می‌گیرد.

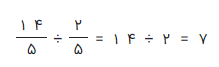
مثال 9: حاصل تقسیم کسرهای زیر چیست؟

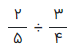
راه حل: به نظر می‌رسد که مخرج این دو کسر با هم برابر نیستند. ولی می‌توانیم با توجه به کوچکترین مضرب مشترک (ک-م-م) بین مخرج‌های این دو کسر، یا به بیان دیگر، بدست آوردن مخرج مشترک آن‌ها، کسرها را به حالتی تبدیل کنیم که مخرج‌های یکسانی داشته باشند.

کوچکترین مضرب مشترک بین ۴ و ۵، عدد ۲۰ است. بنابراین کافی است که صورت و مخرج کسر اول را در ۴ و صورت و مخرج کسر دوم را هم در ۵ ضرب کرده تا به کسرهایی با مخرج برابر برسیم. توجه دارید که ضرب کردن یک عدد (غیر از صفر) در صورت و مخرج کسر، مقدار آن را تغییر نمی‌دهد. این کارها در ادامه دیده می‌شوند.

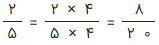
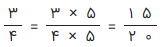
به این ترتیب هر دو کسر، مخرج‌هایی یکسانی داشته و به این ترتیب تقسیم کسری را اجرا می‌کنیم.

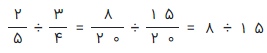
به این ترتیب به یک تقسیم عدد صحیح رسیده‌ایم که می‌توانیم حاصل یا خارج قسمت آن را به صورت یک عدد اعشاری که در اینجا ۰٫۵۳۳۳۳ است، نشان دهیم. ولی به عنوان راه حل کلی برای تقسیم اعداد اعشاری به روش تبدیل به کسر و تقسیم کسرها، ابتدا با شیوه نمایش کسری اعداد اعشاری به طور خلاصه می‌پردازیم.

برای تبدیل هر عدد اعشاری به صورت کسری، کافی است جایگاه آخرین ارقام اعشار را مشخص کرده و در کسر برحسب این جایگاه، مضرب‌هایی از ۱۰ را قرار دهید و همه ارقام بعد از اعشار را در صورت بنویسیم. برای مثال جایگاه یک‌دهم، با مخرج ۱۰ مشخص می‌شود. اگر عدد اعشاری دارای رقمی در جایگاه یکصدم باشد، در مخرج کسر، ۱۰۰ قرار می‌دهیم.

مثال 10: عدد اعشاری ۰٫۴ را به صورت کسری بنویسید.

راه حل: رقم ۴ در این عدد اعشاری، جایگاه دهم دارد، بنابراین برای تبدیل آن به صورت کسری، در مخرج مقدار ۱۰ را قرار می‌دهیم.

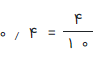
مثال ۱۱: عدد اعشاری ۰٫۱۵ را به صورت کسری بنویسید.

راه حل: آخرین رقم اعشار در ۰٫۱۵، رقم ۵ است که در جایگاه صدم قرار دارد. بنابراین باید برای تبدیل آن به صورت کسری، در مخرج، مقدار ۱۰۰ را قرار داده و همه ارقام بعد از اعشار را در صورت بیاوریم.

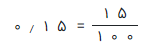
مثال ۱۲: عدد اعشاری ۰٫۲۰۴ را به صورت کسری بنویسید.

راه حل: مشخص است که آخرین رقم اعشار در ۰٫۲۰۴، رقم ۴ است. این رقم در جایگاه هزارم قرار گرفته است. بنابراین در مخرج کسر ۱۰۰۰ قرار خواهیم داد. بقیه ارقام را هم در صورت می‌نویسیم. بنابراین تبدیل آن به صورت کسری به صورت زیر خواهد بود.

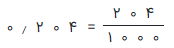
مثال ۱۳: عدد اعشاری ۰٫۰1۴۸ را به صورت کسری بنویسید.

راه حل: آخرین رقم این عدد (یعنی ۸) در جایگاه ده هزارم مشخص شده است. بنابراین در مخرج کسر ۱۰۰۰۰ قرار خواهیم داد. بقیه ارقام (به جز صفر قبل از ارقام) را هم در صورت نمایش می‌دهیم. به این ترتیب ۰٫۰۱۴۸ را به صورت کسری در آورده‌ایم.

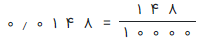
حال زمان انجام تقسیم اعداد اعشاری به کمک کسر فرا رسیده است. به یاد دارید که از قاعده زیر برای تقسیم دو کسر استفاده می‌کنیم.

برای تقسیم دو عدد کسری، کسر مربوط به مقسوم علیه را معکوس کرده و در کسر مقسوم ضرب می‌کنیم.

پس کافی است از طریق ضرب اعداد صحیح، نتیجه تقسیم اعداد اعشاری را به کمک کسر محاسبه کنیم. این موضوع را با نمادهای ریاضی به صورت زیر نمایش می‌دهیم.

$$\large \dfrac{ a}{ b} \div \dfrac{ c}{ d} = \dfrac{ a}{ b} \times \dfrac{ d}{ c} = \dfrac{ a \times d} { b \times c}$$

همانطور که می‌بینید، صورت کسر اول یعنی a در مخرج کسر دوم یعنی d ضرب شده و صورت کسر مربوط به تقسیم را ساخته است. از طرفی مخرج کسر اول یعنی b نیز در صورت کسر دوم یعنی c ضرب شده و مخرج کسر خارج قسمت را تشکیل داده است. به این ترتیب به کمک مثال‌های زیر، نحوه تقسیم دو عدد اعشاری با استفاده از تبدیل آن‌ها به کسر را معرفی می‌کنیم.

نکته: به منظور آشنایی با مراحل تبدیل عدد اعشاری به کسر، متن کسر متعارفی — به زبان ساده را بخوانید تا این کار را به سادگی انجام دهید.

مثال 14: حاصل تقسیم ۰٫۳ را بر ۰٫۴ بدست آورید.

راه حل: همانطور که گفته شد، ابتدا هر دو عدد اعشاری را به صورت کسر در می‌آوریم.

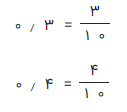
بنابراین تقسیم به صورت زیر نوشته می‌شود.

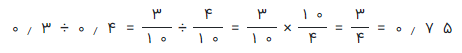
در تساوی آخر، کسر را به عدد اعشاری تبدیل کرده‌ایم. به این ترتیب خارج قسمت تقسیم ۰٫۳ بر ۰٫۴ برابر با ۰٫۷۵ است.

مثال ۱۵: حاصل تقسیم ۱٫۳ بر ۰٫۴ را بدست آورید.

راه حل: ابتدا اعداد را به صورت کسری می‌نویسیم و به کمک رابطه تقسیم کسرها، خارج قسمت را بدست می‌آوریم.

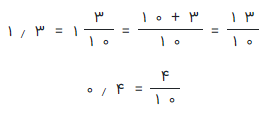
حالا، کسر مربوط به 1٫۳  را بر ۰٫۴ تقسیم می‌کنیم.

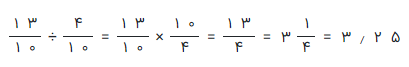
مثال ۱۶: خارج قسمت تقسیم ۱٫۳ را بر ۱٫۲ مشخص کنید.

راه حل: همانطور که اشاره شد، ابتدا اعداد اعشاری را به کسر تبدیل می‌کنیم.

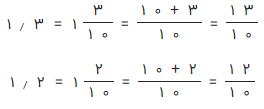
حالا، کسرها را به هم تقسیم می‌کنیم.

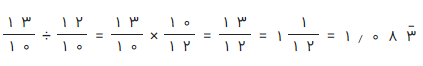
همانطور که می‌بینید، کسر بدست آمده به صورت یک عدد اعشاری با دوره گردش ۳ خواهد بود. خط تیره‌ای که بالای رقم ۳ دیده می‌شود، نشان دهنده دوره گردش یا تکرار این رقم در نتیجه تقسیم است. چنین کسرهایی مانند «یک دوازدهم» را به نام کسرهای مولد اعشار متناوب می‌شناسیم.

تقسیم اعداد اعشاری به روش مستقیم

در این روش، با همان شیوه‌ای که تقسیم را انجام می‌دادیم، محاسبات را انجام می‌دهیم. در ادامه به کمک مثال‌هایی این روش را توضیح می‌دهیم.

مثال ۱۷: حاصل تقسیم ۰٫۶ بر ۱۲ چگونه بدست می‌آید.

راه حل: به شیوه تقسیم مستقیم باید رقم به رقم، عمل تقسیم را انجام دهیم.

در گام اول سعی می‌کنیم که ۰٫۶ را بر ۱۲ تقسیم کنیم. به این ترتیب عمل تقسیم را به صورت نمادین و به شکل زیر می‌نویسیم. قسمت صحیح (صفر) بر ۱۲ بخش‌پذیر نیست، پس به قسمت اعشاری مراجعه می‌کنیم.

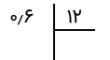
در گام دوم، ابتدا یک ممیز در خارج قسمت قرار می‌دهیم، زیرا به علامت ممیز رسیده‌ایم. چون ۰٫۶ بر ۱۲ بخش پذیر نیست، یک صفر از سمت راست به پایین انتقال داده و برای خارج قسمت هم بعد از ممیز یک صفر اضافه می‌کنیم. برای مشخص کردن محل ممیز در گام‌های بعدی، از یک خط عمودی به رنگ آبی نیز کمک گرفته‌ایم.

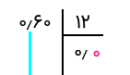
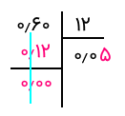
با توجه به اینکه حاصل تقسیم ۶۰ بر ۱۲ مساوی با ۵ است، در قسمت اعشار خارج قسمت، ۵ را اضافه می‌کنیم. از آنجایی که باقی‌مانده صفر شده است، عمل تقسیم پایان یافته.

مثال ۱۸: حاصل تقسیم ۱۲ بر ۰٫۲۳ چیست؟

راه حل: برای حل و بدست آوردن خارج قسمت به همان شیوه قدیمی تقسیم رجوع می‌کنیم. ابتدا از سمت چپ مقسوم علیه یک رقم جدا کرده و سعی می‌کنیم، تقسیم را انجام دهیم. فقط به این نکته توجه داشته باشید، چون آخرین رقم مقسوم علیه در مکان دوم (صدم) قرار دارد، اولین رقم خارج قسمت هم مربوط به مکان دوم (دهگان) است.

اولین رقم از سمت چپ (بعد از علامت ممیز) عدد ۲ است، که مشخص است ۱۲ به ۲ بخش‌پذیر بوده و حاصل تقسیم ۶ خواهد بود که با توجه به مکان دوم آن، باید آن را ۶۰ در نظر بگیریم. ولی از آنجایی که حاصل ضرب ۶۰ در ۰٫۲۳ بزرگتر از ۱۲ است (مقدار 13٫۸)، از ۵ یا به طور دقیق ۵۰ استفاده می‌کنیم، حاصل ضرب ۵۰ در ۰٫۲3 یعنی 11٫۵، کوچکتر از ۱۲ است، پس ۵۰ عدد مناسب خواهد بود.

پس از ضرب کردن 50 در ۰٫۲3، حاصل ۱1٫۵ شده و باقی‌مانده ۰٫۵۰ خواهد شد که از ۰٫۲۳ بزرگتر است. بنابراین باید تقسیم ادامه پیدا کند. این بار ۰٫۵۰ را بر ۰٫۲۳ تقسیم می‌کنیم که خارج قسمت برابر با 2 خواهد بود که آن را در یکان قرار می‌دهیم. حاصل ضرب ۰٫۲۳ در ۲ برابر با ۰٫۴۶ بوده و باقی‌مانده نیز برابر با ۰٫۰۴ حاصل می‌شود. چون این عدد از ۰٫۲۳ کوچکتر است، می‌توانیم همین جا عمل تقسیم را پایان داده و خارج قسمت را ۵۲ و باقی‌مانده را ۰٫۰۴ بدست آوریم.

نکته: در صورتی که نتیجه تقسیم را با دقت بیشتر احتیاج داشته باشیم، با اضافه کردن یک صفر به ۰٫۰۴ می‌توان عمل تقسیم را به کمک ۰٫۰۴۰ ادامه داد. فقط به یاد داشته باشید که در خارج قسمت هم باید علامت ممیز را به کار ببرید.

در تصویرهای زیر گام‌های خلاصه این تقسیم دیده می‌شود.

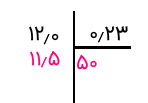
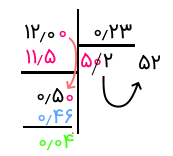
تقسیم اعداد اعشاری به روش تبدیل

در این روش که شاید سریع‌ترین روش تقسیم اعداد اعشاری باشد، ابتدا هم مقسوم و هم مقسوم علیه را به عدد صحیح تبدیل کرده و عمل تقسیم را به شیوه معمول انجام می‌دهیم. فقط باید به این نکته توجه داشته باشید از اعداد ۱۰، ۱۰۰ یا ۱۰۰۰ و ... به شکلی استفاده کنید که همزمان هم مقسوم و هم مقسوم علیه را به عدد صحیح تبدیل کند.

برای مثال اگر قرار باشد ۰٫۴ و ۰٫۰۵ را به ضرب کردن در یک عدد، به صورت صحیح درآوریم، هر دو را باید در ۱۰۰ ضرب کنیم و حاصل این کار به شکل ۴۰۰ و ۵ درخواهد آمد. پس با توجه به بیشترین مکان رقم اعشار هر دو عدد، تبدیل را انجام می‌دهیم. پس مشخص شده، از آنجایی که بیشترین رقم اعشار در بین ۰٫۴ و ۰٫۰۵، رقم ۵ است که در مکان صدم قرار گرفته، هر دو عدد را در ۱۰۰ ضرب می‌کنیم.

مثال ۱۹: حاصل تقسیم ۰٫۴ بر ۰٫۰۵ را بدست آورید.

راه حل: همانطور که گفته شد، ابتدا آن‌ها را با ضرب کردن در ۱۰، ۱۰۰ یا ۱۰۰۰ تبدیل به عدد صحیح می‌کنیم. عدد مناسب در اینجا ۱۰۰ است.

۰٫۴ × ۱۰۰ = ۴۰

۰٫۰۵ × ۱۰۰ = ۵

حالا آن‌ها را بر هم تقسیم می‌کنیم. می‌دانیم خارج قسمت تقسیم عدد ۴۰ بر ۵ برابر با ۸ بوده و باقی‌مانده هم صفر شده که معمولا می‌گوییم باقی‌مانده ندارد. در این حالت می‌گوییم ۴۰ بر ۵ بخش‌پذیر است. این تقسیم را یک تقسیم کمکی می‌نامیم. خارج قسمت تقسیم اصلی با خارج قسمت تقسیم کمکی برابر است فقط باقی‌مانده باید بر ۱۰۰ تقسیم شود که چون باقی مانده وجود ندارد، تغییری در تقسیم رخ نمی‌دهد.

مثال ۲۰: حاصل تقسیم 0٫۵ بر ۰٫۲3 را بدست آورید.

راه حل: اول هر دو را در ۱۰۰ ضرب می‌کنیم چون آخرین رقم اعشار در ۰٫۲۳، که عدد ۳ است، در جایگاه صدگان قرار دارد.

0٫۵ × ۱۰۰ = ۵۰

۰٫۲۳ × ۱۰۰ = ۲۳

حالا بر اساس تقسیم کمکی، ۵۰ را بر ۲۳ تقسیم می‌کنیم. خارج قسمت برابر است با ۲٫۱۷ و باقی‌مانده هم برای تقسیم کمکی، مقدار 0٫۰۹ است. ولی باید توجه داشته باشید که این باقی‌مانده باید بر ۱۰۰ تقسیم شود تا باقی‌مانده تقسیم اصلی را نشان دهد. بنابراین خارج قسمت تقسیم ۰٫۵ بر ۰٫۲۳ همان ۲٫۱۷ بوده ولی باقی‌مانده ۰٫۰۰۰۹ محاسبه می‌شود.

نکته: برای به دست آوردن باقی‌مانده تقسیم، بايد مقدار محاسبه شده برای باقی‌مانده تقسيم جديد (مقسوم و مقسوم علیه تبدیل شده) را بر همان عددی كه مقسوم و مقسوم عليه را در آن ضرب كرده‌ايم، تقسيم كنيم. در غیر این صورت، باقی‌مانده صحیح نخواهد بود.

امتحان کردن عمل تقسیم اعشاری

می‌دانید که بعد از هر تقسیم، بهتر است نتیجه را امتحان کنیم تا مطمئن شویم، خارج قسمت و باقی مانده به صورت درست محاسبه و به دست آمده‌اند. امتحان کردن تقسیم با ضرب کردن خارج قسمت در مقسوم علیه و جمع با باقی‌مانده انجام می‌شود. این محاسبه باید با مقسوم برابر باشد تا درستی نتیجه تقسیم تایید شود. در تقسیم اعداد اعشاری هم به همین گونه حاصل اجرای عملیات تقسیم را امتحان یا آزمون می‌کنیم. این محاسبات باید با مقسوم برابر شود. به این ترتیب امتحان کردن عمل تقسیم اعشاری ما را به همان مقسوم خواهد رساند.

مثال ۲۱: نتیجه (خارج قسمت) تقسیم مثال ۱۹ را امتحان کنید.

راه حل: در مثال ۱۹ دیدیم که خارج قسمت برابر با 40 شد. برای امتحان به صورت زیر عمل می‌کنیم.

۸ × ۰٫۰۵ = ۰٫۴

از طرفی باقی‌مانده هم صفر است و با اضافه کردن صفر به حاصل ضرب بالا، تغییری بوجود نمی‌آید. پس با ضرب مقدار مقسوم علیه در خارج قسمت، به مقسوم رسیدیم، در نتیجه تقسیم به درستی انجام شده است.

مثال ۲۲: درستی تقسیم مثال ۲۰ را نمایش دهید.

راه حل: در مثال ۲۰، مقسوم برابر با ۰٫۵ و مقسوم علیه هم ۰٫۲۳ بود. خارج قسمت ۲٫۱۷ و باقی‌مانده، ۰٫۰۰۰۹ بدست آمد. محاسبات زیر را برای درستی تقسیم انجام می‌دهیم.

۲٫۱۷ × ۰٫۲۳ + ۰٫۰۰۰۹ = ۰٫۴۹۹۱ + ۰٫۰۰۰۹ = ۰٫۵

پس در اینجا هم عمل تقسیم به درستی صورت گرفته است.

آزمون سنجش یادگیری تقسیم اعداد اعشاری

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث تقسیم اعداد اعشاری را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.