تقسیم چکشی – آموزش به زبان ساده + مثال و تمرین

در آموزش‌های پیشین مجله فرادرس، با تقسیم عدد صحیح و تقسیم ذهنی آشنا شدیم. در این آموزش از مجله فرادرس، به یکی از معروف‌ترین روش‌های تقسیم اعداد، یعنی تقسیم چکشی می‌پردازیم و در قالب مثال‌هایی به‌صورت گام به گام آن را شرح خواهیم داد.

احتمالاً این پرسش برایتان پیش آمده است که دلیل نام‌گذاری تقسیم چکشی چیست. پاسخ این پرسش آن است که ظاهر این تقسیم شبیه یک چکش است و در نهایت ارقام را مثل میخ یکی یکی می‌کوبد و پایین می‌برد. البته در زبان انگلیسی به این تقسیم، «تقسیم طولانی» (Long Division) می‌گویند.

آشنایی با نحوه انجام تقسیم چکشی، دلیل نام‌گذاری آن و شباهتش با کوبیدن میخ را روشن خواهد کرد. پیش از آن، با مفاهیم مقسوم، مقسوم‌علیه و خارج‌قسمت آشنا می‌شویم.

فرض کنید می‌خواهیم عدد ۱۵ را بر ۳ تقسیم کنیم. عددی که تقسیم می‌شود (در این مورد، 15) را «مقسوم» (Dividend) می‌گوییم و عددی که مقسوم بر آن تقسیم می‌شود (در اینجا 3) «مقسوم‌علیه» (Divisor) نامیده می‌شود. حاصل تقسیم «خارج‌قسمت» (Quotient) نام دارد. اگر عددی را نتوانستیم به چند قسمت مساوی تقسیم کنیم و چیزی باقی بماند، به آن «باقیمانده» (Remainder) می‌گوییم. زمانی که نتیجه تقسیم دو عدد صحیح، با یک خارج قسمت صحیح قابل بیان نباشد، مقداری باقی می‌ماند که به آن باقیمانده می‌گویند.

برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

تقسیم را به شیوه‌های مختلفی نشان می‌دهند. تصویر زیر سه مورد از رایج‌ترین شیوه‌های نمایش تقسیم را نشان می‌دهد و در آن، مقسوم، مقسوم علیه، خارج‌ قسمت و باقیمانده نشان داده شده است. می‌بینیم که تقسیم وسط روش تقسیم چکشی را نشان می‌دهد که در ادامه با آن آشنا خواهیم شد.

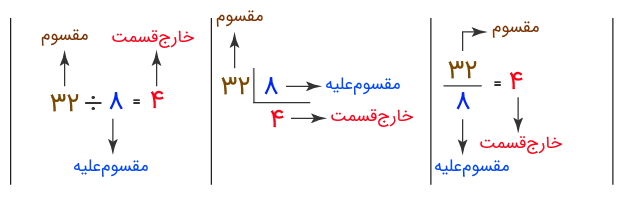
برای آشنایی بیشتر با مقسوم، مقسوم‌علیه و خارج‌قسمت، به آموزش «مقسوم ، مقسوم علیه و باقیمانده چیست؟ — به زبان ساده» مراجعه کنید.

روش انجام تقسیم چکشی

تقسیم چکشی را می‌توان در چند گام بسیار ساده انجام داد. در ادامه، این مراحل را بیان می‌کنیم. برای مثال، فرض کنید می‌خواهیم ۱۰۵ را بر ۸ تقسیم کنیم.

گام اول: ابتدا باید مقسوم و مقسوم‌علیه را مشخص کنیم. در مثالی که بیان کردیم، مقسوم ۱۰۵ و مقسوم‌علیه ۸ است.

گام دوم: تعداد ارقام مقسوم‌علیه را می‌بینیم و به اندازه آن از سمت چپ از ارقام مقسوم جدا می‌کنیم.

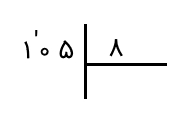
گام سوم: بررسی می‌کنیم که آیا تعداد ارقامی که جدا کرده‌ایم کافی است یا نه. این کار را با تقسیم ارقامی که جدا کرده‌ایم بر عدد مقسوم‌علیه انجام می‌دهیم. در اینجا می‌بینیم که تعداد ارقامی که جدا کرده‌ایم، کم است، زیرا ۱ را نمی‌توان بر ۸ تقسیم کرد و از آن کوچک‌تر است. به عبارت دیگر می‌توان این پرسش را مطرح کرد که در عدد ۱ چند ۸ وجود دارد؟ و جواب صفر است. بنابراین، یک رقم دیگر را نیز در کنار رقمی که جدا کرده بودیم، جدا می‌کنیم. برای مثالی که داریم، عدد ۱۰ را جدا می‌کنیم.

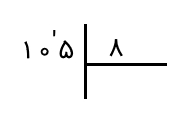
اکنون می‌توان ۱۰ را بر ۸ تقسیم کرد.

گام چهارم: اکنون این پرسش را مطرح می‌کنیم که چند تا ۸ در ۱۰ قرار دارد و جوابمان ۱ است. بنابراین، عدد ۱ را در بخش خارج‌قسمت می‌نویسیم.

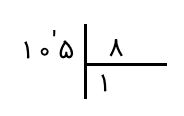
گام پنجم: عدد خارج‌‌قسمت را در مقسوم‌علیه ضرب کرده و حاصل را از سمت راست زیر عدد ۱۰ می‌نویسیم که جدا کرده بودیم.

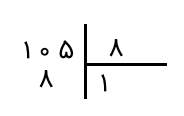
گام ششم: اکنون ۸ را از ۱۰ کم می‌کنیم و حاصلش را پایین آن‌ها می‌نویسیم.

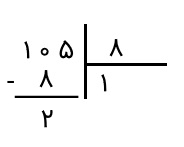
گام هفتم: حال عدد ۵ را پایین می‌آوریم و در کنار حاصل تقسیم، یعنی ۲، می‌نویسیم.

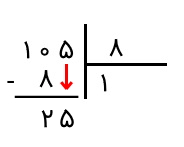
گام هشتم: در اینجا گویی یک تقسیم جدید داریم و باید ۲۵ را بر ۸ تقسیم کنیم. این پرسش را مطرح می‌کنیم که در ۲۵ چند ۸ قرار دارد. با دانستن ضرب ۲۴ = ۸ × ۳ خواهیم دید که جواب عدد ۳ است. بنابراین، ۳ را در خارج قسمت و کنار ۱ قرار می‌دهیم.

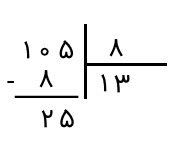
گام نهم: عدد ۳ را که نوشتیم، آن را در مقسوم‌علیه ضرب می‌کنیم و حاصل را زیر مقسوم جدید، یعنی ۲۵، می‌نویسیم.

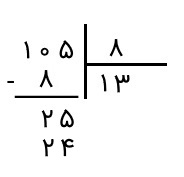
گام دهم: عدد حاصل را از مقسوم‌ جدید، یعنی ۲۵ کم می‌کنیم و حاصل را می‌نویسیم.

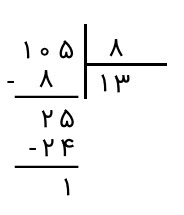
می‌بینیم که عدد دیگری نیست که پایین بیاوریم. همچنین، باقیمانده، یعنی ۱، از مقسوم‌علیه، یعنی ۸، کوچک‌تر است و تقسیم پایان می‌پذیرد.

خلاصه مراحل تقسیم چکشی: ابتدا از سمت چپ یک رقم از ۱۰۵ جدا می‌کنیم و می‌بینیم که بزرگ‌تر از ۸ نیست و نمی‌توانیم آن را بر ۸ تقسیم کنیم. پس دو رقم را جدا می‌کنیم. اکنون عدد ۱۰ را می‌توان بر ۸ تقسیم کرد که حاصلش می‌شود ۱. این عدد ۱ را در خارج قسمت می‌نویسیم و آن را در مقسم علیه (۸) ضرب می‌کنیم. حاصل ۸ می‌شود، آن را زیر عدد ۱۰ می‌نویسیم و از آن کم می‌کنیم. حاصلش می‌شود ۲. اکنون آن عدد ۵ بالا را پایین می‌آوریم و در کنار ۲ قرار می‌دهیم. حال عدد ۲۵ را داریم. اکنون باید ۲۵ را بر ۸ تقسیم کنیم. حاصل این تقسیم ۳ است. ۳ را در کنار ۱ خارج قسمت می‌نویسیم. اکنون 3 را در مقسوم علیه ضرب می‌کنیم و حاصل (یعنی ۲۴) را زیر مقسوم می‌نویسیم. سپس ۲۴ را از ۲۵ کم می‌کنیم که حاصلش می‌شود ۱ و کوچک‌تر از مقسوم‌ علیه است و اینجاست که تقسیم متوقف می‌شود. تصویر زیر خلاصه انجام مراحل را نشان می‌دهد.

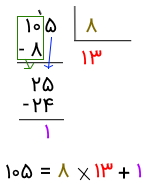
پس در این مثال، عدد ۱۰۵ مقسوم است، عدد ۸ مقسوم علیه، عدد ۱۳ خارج قسمت و عدد ۱ باقیمانده.

فیلم آموزش نقاشی – ویژه کودکان در فرادرس

کلیک کنید

تقسیم چکشی چهار رقمی بر دو رقمی

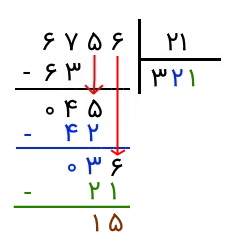
مثالی که بیان کردیم، مثال نسبتاً ساده‌ای بود. اکنون یک مثال دیگر را بررسی می‌کنیم. در این مثال، یک عدد چهار رقمی را بر عددی دو رقمی تقسیم می‌کنیم. می‌خواهیم تقسیم ۶۷۵۶ بر ۲۱ را انجام دهیم. حالا که مراحل تقسیم را می‌دانیم، برخی گام‌ها را سریع‌تر پیش می‌بریم.

ابتدا تقسیم را به‌شکل مناسب می‌نویسیم.

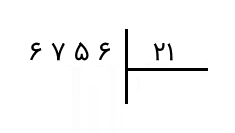
برای شروع، ابتدا از چپ دو رقم را جدا می‌کنیم و بررسی می‌کنیم که این عدد دورقمی بزرگ‌تر از مقسوم‌علیه (عدد ۲۱)‌ باشد. می‌بینیم که ۶۷ بزرگ‌تر از ۲۱ است. بنابراین، جدا کردن این دو رقم کافی است. حال این سؤال را از خودمان می‌پرسیم که «چند تا ۲۱ در ۶۷ وجود دارد؟» با کمی سعی و خطا و بررسی، می‌بینیم که ۳ تا ۲۱ تایی در ۶۷ قرار دارد. پس عدد ۳ را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم.

حاصل‌ضرب ۳ در ۲۱ برابر با ۶۳ است. این عدد را از ۶۷ کم می‌کنیم و حاصل را می‌نویسیم.

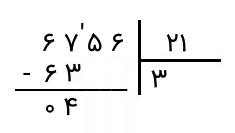
در مرحله بعد، می‌بینیم که نمی‌توان ۴ را بر ۲۱ تقسیم کرد. پس یک رقم را از مقسوم اصلی پایین می‌آوریم و به عدد ۴۵ می‌رسیم که از ۲۱ بزرگ‌تر است و می‌توانیم آن را بر ۲۱ تقسیم کنیم.

اکنون از خودمان می‌پرسیم که چند تا ۲۱ در ۴۵ می‌تواند قرار داشته باشد. جواب ۲ است. پس ۲ را در کنار ۳ در خارج‌قسمت می‌نویسیم و آن را مشابه مراحل قبل در ۲۱ ضرب می‌کنیم و عدد حاصل (یعنی ۴۲) را زیر ۴۵ می‌نویسیم و از آن کم می‌کنیم. حاصل تفریق را نیز می‌نویسیم که عدد ۳ است.

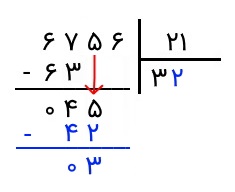
کار را مشابه مراحل قبل ادامه می‌دهیم. می‌بینیم که ۳ از ۲۱ کوچک‌تر است. پس یک رقم دیگر را پایین می‌آوریم و به عدد ۳۶ می‌رسیم. اکنون می‌توانیم ۳۶ را بر ۲۱ تقسیم کنیم. می‌بینیم که یک ۲۱ تایی در ۳۶ می‌تواند وجود داشته باشد. پس رقم ۱ را در کنار دو رقم دیگر در خارج قسمت می‌نویسیم.

پس از آنکه رقم ۱ را نوشتیم، آن را در ۲۱ ضرب می‌کنیم و حاصل را که برابر با ۲۱ است، زیر عدد ۳۶ یادداشت می‌کنیم. حال باید ۲۱ را از ۳۶ کم کنیم که حاصل آن می‌شود ۱۵. مشاهده می‌کنیم که ۱۵ از ۲۱ کوچک‌تر است و نمی‌توان آن را بر ۲۱ تقسیم کرد. رقمی هم از مقسوم اصلی باقی نمانده که آن را پایین بیاوریم. پس اینجا تقسیم خاتمه پیدا می‌کند.

تقسیم چکشی اعداد اعشاری

تقسیم چکشی اعداد اعشاری شاید کمی دشوار به نظر برسد. اما با یک کار ساده می‌توان تقسیم را مانند آنچه که برای اعداد صحیح گفتیم، انجام داد.

برای مثال، فرض کنید می‌خواهیم ۳۷٫۴۵ را بر ۷ تقسیم کنیم. این مثال را بدون تغییر اعداد مقسوم و مقسوم‌علیه حل می‌کنیم. بدین منظور، از اعشار یک خط عمودی به پایین رسم می‌کنیم تا مرز اعشار را بشناسیم و تقسیم را به‌درستی انجام دهیم.

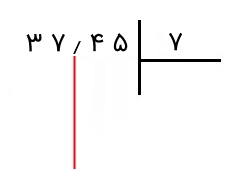
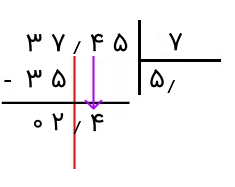
اکنون از سمت چپ شروع می‌کنیم. بخش صحیح عدد را می‌بینیم. مانند دو عدد صحیح، یک رقم از چپ جدا می‌کنیم و می‌بینیم که ۳ کوچک‌تر از ۷ است. پس یک رقم دیگر نیز جدا می‌کنیم. اکنون عدد ۳۷ را داریم. می‌خواهیم ببینیم چند ۷ در ۳۷ وجود دارد. عدد ۵ جوابی است که به آن می‌رسیم. آن را در خارج قسمت می‌نویسیم. اکنون عدد را در مقسوم‌علیه ضرب می‌کنیم و حاصل آن را زیر بخش صحیح عدد مقسوم‌علیه، یعنی ۳۷،‌ می‌نویسیم. سپس آن را از ۳۷ کم می‌کنیم. حاصل را که ۲ است، زیر آن می‌نویسیم.

اکنون، مشابه آنچه برای اعداد صحیح انجام می‌دادیم، اعشار و یک رقم از بالا را به پایین می‌آوریم و کنار رقم ۲ قرار می‌دهیم. همان‌طور که مشخص است، به عدد ۲٫۴ می‌رسیم.

نکته‌ای که در اینجا باید به آن دقت کنیم و بسیار مهم است، این است که وقتی اعشار را پایین می‌آوریم، باید یک اعشار بعد از رقم خارج‌قسمت قرار دهیم.

اکنون که بعد از رقم ۵ اعشار گذاشته‌ایم، رقمی که بعد از اعشار قرار گیرد، در واقع ارزش مکانی آن دهم است. در واقع، اکنون ۲٫۴ را بر ۷ تقسیم می‌کنیم و خارج‌قسمت ارزش دهم دارد. برای راحتی می‌توانیم در ذهنمان دو اعشار را به‌طور فرضی حذف کنیم و تقسیم ۲۴ بر ۷ را انجام دهیم و محاسبه نیز درست خواهد بود.

بنابراین، از خودمان می‌پرسیم که چند تا ۷ در ۲۴ قرار دارد و جوابمان رقم ۳ است. دقت کنید که معادل اعشاری این پرسش این‌گونه است: چند تا یک‌دهمِ رقم ۷ در ۲٫۴ قرار دارد که جواب باز هم ۳ است. یک‌دهم ۷ که می‌شود ۰٫۷ و ۳ تا از آن در ۲٫۴ قرار دارد.

پس، ۳ را بعد از اعشار خارج‌قسمت قرار می‌دهیم و آن را در ۷ ضرب می‌کنیم. دقت کنید که داریم ۰٫۳ را در ۷ ضرب می‌کنیم، چون ۳ بعد از اعشار است و ارزش مکانی آن دهم است.

در واقع، اکنون باید ۲۷ را بر ۷ تقسیم کنیم. عدد ۳ برای جواب آن مناسب است. بنابراین، گویی همان ۲٫۴ را بر ۷ تقسیم کرده‌ایم و چون اعشار قرار داده‌ایم، عدد خارج قسمت ۰٫۳ است.

حال آن ۳ را در ۷ ضرب می‌کنیم که حاصلش می‌شود ۲٫۱. آن را زیر ۲٫۴ می‌نویسیم و از آن کم می‌کنیم.

حاصل برابر با ۰٫۳ خواهد بود. اکنون ۵ را پایین می‌آوریم و باید ۰٫۳۵ را بر ۷ تقسیم کنیم.

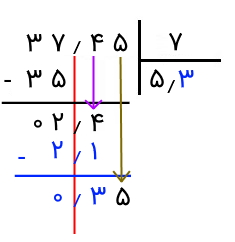
تا حالا خارج قسمت ۵٫۳ است. اکنون، ارزش رقم بعد از ۳ صدم‌ است. یعنی باید از خودمان بپرسیم که چند تا صدم را باید در ۷ ضرب کنیم که حاصلش بشود ۰٫۳۵. جایگاه صدم یعنی دو رقم اعشار و ۰٫۳۵ هم دو رقم اعشار دارد. بنابراین، با توجه به اینکه خارج قسمت در این مرحله دو رقم اعشار دارد و مقسوم جدید، یعنی ۰٫۳۵، نیز دو رقم اعشار دارد، می‌توانیم برای راحتی و به‌دست آوردن رقم خارج قسمت، اعشار را در نظر نگیریم و از خودمان بپرسیم که چند تا ۷ می‌شود ۳۵. جواب ۵ است.

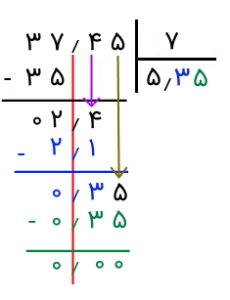
بنابراین، کافی است رقم ۵ را در کنار رقم ۳ در خارج‌قسمت قرار دهیم. در واقع، ۰٫۳۵ را اگر بر ۷ تقسیم کنیم، به عدد ۰٫۰۵ می‌رسیم. به عبارت دیگر، ۰٫۰۵ را اگر در ۷ ضرب کنیم، به عدد ۰٫۳۵ می‌رسیم. با نوشتن این عدد زیر مقسوم جدید، به باقیمانده صفر می‌رسیم.

روش دیگر تقسیم چکشی اعداد اعشاری

یک روش دیگر برای تقسیم چکشی اعداد اعشاری، این است که دو عدد مقسوم و مقسوم‌علیه را به اعدادی صحیح تبدیل کنیم و در آخر، در صورت نیاز، تغییرات را برگردانیم. با یک مثال، این روش را توضیح می‌دهیم. همان مثال قبلی را در نظر بگیرید. فرض کنید می‌خواهیم ۳۷٫۴۵ را بر ۷ تقسیم کنیم.

می‌بینیم که مقسوم یک عدد اعشاری است. برای آنکه آن را به یک عدد صحیح تبدیل کنیم، باید اعشار را دو رقم به سمت راست ببریم و به عدد ۳۷۴۵ برسیم. اکنون می‌توانیم تقسیم ۳۷۴۵ بر ۷ را انجام دهیم، البته با رعایت یک نکته بسیار مهم. چون اعشار مقسوم را دو رقم به سمت راست جابه‌جا کرده‌ایم، هر جوابی را که به‌دست آوردیم، باید دو رقم اعشار به سمت چپ جدا کنیم تا اثر جابه‌جایی دو رقم به راست حذف شود.

ابتدا تقسیم ۳۷۴۵ بر ۷ را انجام می‌دهیم. چون اکنون این تقسیم را آموخته‌ایم، از بیان گام‌های آن صرف‌نظر می‌کنیم. تصویر زیر حاصل این تقسیم را نشان می‌دهد.

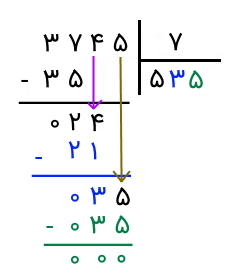
می‌بینیم که جواب ۵۳۵ شده است. اما جواب نهایی این نیست. باید دو رقم اعشار به سمت چپ بیایم و جواب را به‌شکل ۵٫۳۵ بنویسیم. در نهایت، می‌بینیم که پاسخ مشابه بخش قبل است.

مثال‌های تقسیم چکشی

در این بخش، چند مثال را از تقسیم چکشی بررسی می‌کنیم.

مثال اول

عدد ۲۳٫۴۵ را بر ۰٫۲۱ تقسیم کنید.

جواب: می‌بینیم که دو عدد اعشاری هستند. ساده‌ترین کار این است که این دو عدد را به اعدادی صحیح تبدیل کنیم، سپس تقسیم چکشی را انجام دهیم. برای تبدیل مقسوم به یک عدد صحیح، کافی است اعشار را دو رقم به سمت راست جابه‌جا کنیم. در واقع، با ضرب عدد ۱۰۰ در آن، این کار را انجام می‌دهیم. عدد مقسوم‌علیه را نیز با همین کار به یک عدد صحیح تبدیل می‌کنیم. با توجه به اینکه هم اعشار مقسوم و هم اعشار مقسوم‌علیه را دو رقم به سمت راست جابه‌جا کرده‌ایم، در پایان نیازی به تغییر جواب نیست. دلیل واضح‌تر این امر آن است که یک تقسیم داریم که هم مقسوم و هم مقسوم‌علیه را در عدد ۱۰۰ ضرب کرده‌ایم و به همین دلیل، اصل تقسیم تغییری نمی‌کند.

اکنون به سراغ تقسیم چکشی می‌رویم و ۲۳۴۵ را بر ۲۱ تقسیم می‌کنیم. در این مثال، باید عدد چهار رقمی را بر عددی دو رقمی تقسیم کنیم. می‌خواهیم تقسیم ۲۳۴۵ بر ۲۱ را انجام دهیم. ابتدا تقسیم را به‌شکل مناسب چکشی می‌نویسیم. برای شروع، ابتدا از چپ دو رقم را جدا می‌کنیم و بررسی می‌کنیم که این عدد دورقمی بزرگ‌تر از مقسوم‌علیه (عدد ۲۱)‌ باشد. می‌بینیم که ۲۳ بزرگ‌تر از ۲۱ است. در نتیجه، جدا کردن این دو رقم کافی است. حال این سؤال را از خودمان می‌پرسیم که «چند تا ۲۱ در ۲۳ وجود دارد؟» با کمی سعی و خطا و بررسی، می‌بینیم که ۱ تا ۲۱ تایی در ۲۳ قرار دارد. پس عدد ۱ را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم.

حاصل‌ضرب ۱ در ۲۱ برابر با ۲۱ است. این عدد را از ۲۳ کم می‌کنیم و حاصل را که ۲ است، می‌نویسیم.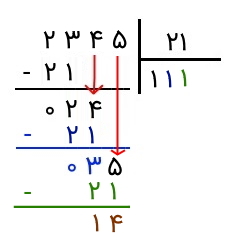

در مرحله بعد، می‌بینیم که نمی‌توان ۲ را بر ۲۱ تقسیم کرد. پس یک رقم را از مقسوم اصلی پایین می‌آوریم و به عدد ۲۴ می‌رسیم که از ۲۱ بزرگ‌تر است و می‌توانیم آن را بر ۲۱ تقسیم کنیم. اکنون از خودمان می‌پرسیم که چند تا ۲۱ در ۲۴ می‌تواند قرار داشته باشد. جواب باز هم ۱ است. پس ۱ را در کنار ۱ قبلی در خارج‌قسمت می‌نویسیم و آن را مشابه مراحل قبل در ۲۱ ضرب می‌کنیم و عدد حاصل (یعنی ۲۱) را زیر ۲۴ می‌نویسیم و از آن کم می‌کنیم. حاصل تفریق را نیز می‌نویسیم که عدد ۳ است.

کار را مشابه مراحل قبل ادامه می‌دهیم. می‌بینیم که ۳ از ۲۱ کوچک‌تر است. پس یک رقم دیگر را پایین می‌آوریم و به عدد ۳۵ می‌رسیم. اکنون می‌توانیم ۳۵ را بر ۲۱ تقسیم کنیم. می‌بینیم که یک ۲۱ تایی در ۳۶ می‌تواند وجود داشته باشد. پس رقم ۱ را در کنار دو رقم دیگر در خارج قسمت می‌نویسیم. پس از آنکه رقم ۱ را نوشتیم، آن را در ۲۱ ضرب می‌کنیم و حاصل را که برابر با ۲۱ است، زیر عدد ۳۵ یادداشت می‌کنیم. حال باید ۲۱ را از ۳۵ کم کنیم که حاصل آن می‌شود ۱۴. مشاهده می‌کنیم که ۱۴ از ۲۱ کوچک‌تر است و نمی‌توان آن را بر ۲۱ تقسیم کرد. رقمی هم از مقسوم اصلی باقی نمانده که آن را پایین بیاوریم. پس اینجا تقسیم خاتمه پیدا می‌کند.

مراحل انجام تقسیم در بالا نشان داده شده است.

بنابراین، برای تقسیم ۲۳۴۵ بر ۲۱، خارج‌قسمت ۱۱۱ و باقیمانده ۱۴ به‌دست آمد. اما نکته مهم در اینجا، باقیمانده است. دو رقم اعشار را باید بر باقیمانده اعمال کنیم. دقت کنید که باقیمانده باید حتماً از مقسوم‌علیه کوچک‌تر باشد.

پس، در نهایت، می‌توان گفت برای تقسیم ۲۳٫۴۵ بر ۰٫۲۱، خارج‌قسمت برابر با ۱۱۱ و باقیمانده ۰٫۱۴ است.

مثال دوم

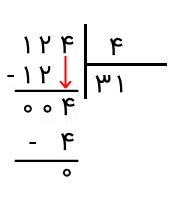
عدد 124 را بر ۴ تقسیم کنید.

جواب: همان‌طور که می‌بینیم، مقسوم ۳ رقم و مقسوم‌علیه ۱ رقم دارد. گام‌های گفته شده در بالا را به کار می‌گیریم. مشاهده می‌کنیم که با انتخاب یک رقم از سمت چپ از عدد ۱۲۴، عمل تقسیم بر ۴ امکان‌پذیر نیست. بنابراین دو رقم را جدا می‌کنیم که عدد ۱۲ است. می‌دانیم که ۱۲ تقسیم بر ۴، خارج‌قسمتی برابر با ۳ و باقیمانده‌ای صفر خواهد داشت. خارج قسمت برابر با ۳ است. این عدد را در بخش خارج‌قسمت می‌نویسیم.

حال، باقیمانده را براساس خارج قسمت جدید محاسبه می‌کنیم که برابر با ۴ است. این باقیمانده را به‌عنوان مقسوم جدید در نظر می‌گیریم. از آنجا که باقیمانده از مقسوم علیه کوچکتر نیست، عملیات تقسیم ادامه پیدا می‌کند. به تعداد یک رقم از سمت چپ مقسوم جدید جدا می‌کنیم. حاصل برابر با ۴ است که خارج قسمت تقسیم آن بر مقسوم علیه (یعنی ۴) برابر با ۱ است. واضح است که باقیمانده هم صفر خواهد بود.

با کنار هم قرار دادن خارج‌قسمت‌ها از چپ به راست برای گام‌های طی‌شده، خارج قسمت برابر با ۳۱ خواهد بود از طرفی، باقیمانده هم صفر است.

مثال سوم

حاصل تقسیم عدد ۵۰۷۰ بر ۹۹ را به‌دست آورید.

جواب: ابتد دو رقم از چپ جدا می‌کنیم که چون ۵۰ از ۹۹ کوچک‌تر است، کافی نیست. پس یک رقم دیگر نیز جدا می‌کنیم. اکنون ۵۰۷ از ۹۹ بزرگ‌تر است. اکنون این سؤال را از خودمان می‌پرسیم که «چند تا ۹۹ در ۵۰۷ وجود دارد؟» می‌بینیم که ۵ تا ۹۹ تایی در ۵۰۷ قرار دارد. بنابراین، عدد ۵ را در خارج قسمت می‌نویسیم و آن را در مقسوم‌علیه ضرب می‌کنیم. حاصل‌ضرب ۵ در ۹۹ برابر با ۴۹۵ است. این عدد را از ۵۰۷ کم می‌کنیم و حاصل را می‌نویسیم.

در مرحله بعد، می‌بینیم که نمی‌توان ۱۲ را بر ۹۹ تقسیم کرد. پس یک رقم را از مقسوم اصلی پایین می‌آوریم و به عدد ۱۲۰ می‌رسیم که از ۹۹ بزرگ‌تر است و می‌توانیم آن را بر ۹۹ تقسیم کنیم. اکنون از خودمان می‌پرسیم که چند تا ۹۹ در ۱۲۰ می‌تواند قرار داشته باشد. جواب ۱ است. پس ۱ را در کنار ۵ در خارج‌قسمت می‌نویسیم و آن را مشابه مراحل قبل در ۹۹ ضرب می‌کنیم و عدد حاصل (یعنی ۹۹) را زیر ۱۲۰ می‌نویسیم و از آن کم می‌کنیم. حاصل تفریق را نیز می‌نویسیم که عدد ۲۱ است.

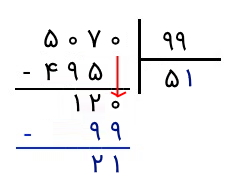
مشاهده می‌کنیم که ۲۱ از ۹۹ کوچک‌تر است و نمی‌توان آن را بر ۹۹ تقسیم کرد. رقمی هم از مقسوم اصلی باقی نمانده که آن را پایین بیاوریم. پس اینجا تقسیم خاتمه پیدا می‌کند.

آزمون تقسیم چکشی

در این بخش برای درک بهتر مفهوم تقسیم چکشی، چند پرسش چهار گزینه‌ای به صورت آزمون مطرح شده است.

باقیمانده تقسیم ۴۲۶ بر ۴ برابر است با:

۰

۲

۴

۶

مشاهده گزینه صحیح

پاسخ تشریحی

باقیمانده تقسیم ۴۲۶ بر ۴ را می‌توانیم با توجه به روش توضیح داده شده به‌دست آوریم. مقدار آن برابر ۲ است. 

اگر مقسوم‌علیه برابر ۸، خارج قسمت برابر ۷۱ و باقی‌مانده برابر ۴ باشد، مقدار مقسوم برابر است با: 

۵۶۲

۵۶۰

۵۷۶

۵۷۲

مشاهده گزینه صحیح

پاسخ تشریحی

برای به‌دست آوردن مقسوم، تنها کافی است خارج قسمت را در مقسوم‌علیه ضرب و حاصل به‌دست آمده را با مقدار باقیمانده جمع کنیم. با انجام این کار، مقدار مقسوم برابر ۵۷۲ به‌دست می‌آید. 

کدام یک از گزینه‌های زیر را می‌توان به جای A در تصویر زیر قرار داد؟ 

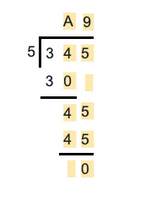
۳

۴

۵

۶

مشاهده گزینه صحیح

پاسخ تشریحی

یکای مقسوم برابر ۵ است. حاصل‌ضرب A در یکای مقسوم باید به گونه‌ای باشد که پاسخ ۳۰ به‌دست بیاید. با انجام این کار، مقدار A برابر ۳۰ به‌دست می‌آید. 

باقیمانده تقسیم ۴۳۵۱ بر ۶ برابر است با: 

۲

۱

۰

۴

مشاهده گزینه صحیح

پاسخ تشریحی

باقیمانده تقسیم ۴۳۵۱ بر ۶ برابر یک و خارج قسمت برابر ۷۲۵ است. 

خارج قسمت و باقیمانده تقسیم ۹۴۲۴۵ بر ۷۴ برابر است با:

خارج قسمت برابر ۱۲۷۳ و باقیمانده برابر ۲۳ است. 

خارج قسمت برابر ۱۲۷۳ و باقیمانده برابر ۳۲ است. 

خارج قسمت برابر ۱۳۷۳ و باقیمانده برابر ۲۳ است. 

خارج قسمت برابر ۱۲۷۰ و باقیمانده برابر ۲۳ است. 

مشاهده گزینه صحیح

پاسخ تشریحی

مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

ورود / ثبت‌نام

باقیمانده تقسیم ۲۴۹۶ بر ۳۲ کدام است؟ 

۰

۱

۴

۵

مشاهده گزینه صحیح

پاسخ تشریحی

مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

ورود / ثبت‌نام

اگر خارج قسمت تقسیم عددی بر ۸۸ برابر ۶۹ و باقیمانده آن برابر ۱۸ باشد، آن عدد برابر است با:

۶۱۹۰

۶۰۹۰

۷۰۹۰

۶۲۹۰

مشاهده گزینه صحیح

پاسخ تشریحی

مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

ورود / ثبت‌نام

جمع‌بندی

در این آموزش از مجله فرادرس، ابتدا روش انجام تقسیم چکشی را بیان کردیم، سپس به بررسی مثال‌هایی پرداختیم و آن‌ها را گام به گام و به زبان ساده حل کردیم.