مقسوم ، مقسوم علیه و باقیمانده چیست؟ – به زبان ساده
در آموزشهای پیشین مجله فرادرس، با تقسیم اعداد صحیح و تقسیم اعداد اعشاری آشنا شدیم. در این آموزش از مجله فرادرس میخواهیم به این پرسشها پاسخ دهیم: مقسوم چیست؟ مقسوم علیه چیست؟ خارج قسمت چیست؟ باقیمانده چیست؟
مقایسه تقسیم و ضرب
معلمان در کلاسهای مختلف ریاضی آموزش تقسیم را معمولاً با توضیح دادن ضرب شروع میکنند. عبارت ریاضی 5 × 3 نشاندهنده سه گروه از چیزهاست که هر کدام پنج چیز دیگر در داخل خود دارند. برای یافتن حاصلضرب، دانشآموزان میتوانند شکلی مانند زیر رسم کنند.
دانشآموزان همچنین میتوانند از جمع مکرر برای یافتن حاصلضرب استفاده کنند. آنها میتوانند عدد 3 را پنج بار با هم جمع کنند: ۱۵ = 3 + 3 + 3 + 3 + 3.
به یاد داشته باشید که ضرب تقسیم را «خنثی» میکند و تقسیم ضرب را «خنثی» میکند. به عبارت دیگر، از آنجا که 15 = 5 × 3، آنگاه 3 = 5 ÷ 15 (و بهطور مشابه، 5 = 3 ÷ 15). از آنجا که تقسیم و ضرب عملیات معکوس هم هستند، دانشآموزان میتوانند از راههای مشابه برای نمایش هردو عملیات استفاده کنند. در عبارت 3 ÷ 15، میتوان از پانزده مورد شروع کرد و دید که با دستههای سهتایی چند گروه را میتوان ساخت. در شکل زیر نتیجه این دستهبندی رسم شده است.
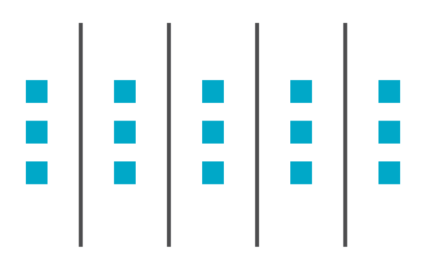
از آنجا که ضرب نوعی جمع مکرر است، میتوان نتیجه گرفت که تقسیم نیز شکلی از تفریق مکرر است. بهعنوان مثال، 3 ÷ 15 یعنی اینکه مکرراً 3 را از 15 کم کنید تا به صفر برسید:
.0 = 3 = 3 – 3 = 3 – 6 = 3 – 9 = 3 – 12 = 3 - 15
مقسوم و مقسوم علیه چیست ؟
دیدیم که فرایند تقسیم مستلزم تفریق 3 به تعداد 5 بار متوالی بود و نوشتیم 5 = 3 ÷ 15. عددی که تقسیم میشود (در این مورد، 15) را «مقسوم» (Dividend) مینامند و عددی را که مقسوم بر آن تقسیم میشود (در اینجا 3) «مقسومعلیه» (Divisor) نامیده میشود.
حاصل تقسیم «خارجقسمت» (Quotient) نام دارد. اگر عددی را نتوانستیم به چند قسمت مساوی تقسیم کنیم و چیزی باقی بماند، به آن «باقیمانده» (Remainder) میگوییم. زمانی که نتیجه تقسیم دو عدد صحیح، با یک خارج قسمت صحیح قابل بیان نباشد، مقداری باقی میماند که به آن باقیمانده میگویند.
تقسیم را به شیوههای مختلفی نشان میدهند. تصویر زیر سه مورد از رایجترین شیوههای نمایش تقسیم را نشان میدهد و در آن، مقسوم، مقسوم علیه، خارج قسمت و باقیمانده نشان داده شده است.
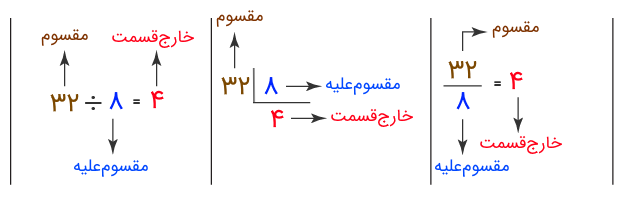
روش تقسیم کردن اعداد
منابع مختلف روشهای متفاوتی برای انجام تقسیم و حل مسائل مربوط به آن ارائه دادهاند. در اینجا روش استاندارد تقسیم را توضیح میدهیم. در آموزش «تقسیم عدد صحیح — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» با تقسیم آشنا شدیم و روند تقسیم دو عدد را بیان کردیم. اکنون برای یادآوری، دو عدد را بر هم تقسیم میکنیم. فرض کنید میخواهیم عدد ۱۰۵ را بر ۸ تقسیم کنیم.
ابتدا از سمت چپ یک رقم از ۱۰۵ جدا میکنیم و میبینیم که بزرگتر از ۸ نیست و نمیتوانیم آن را بر ۸ تقسیم کنیم. پس دو رقم را جدا میکنیم. اکنون عدد ۱۰ را میتوان بر ۸ تقسیم کرد که حاصلش میشود ۱. این عدد ۱ را در خارج قسمت مینویسیم و آن را در مقسم علیه (۸) ضرب میکنیم. حاصل ۸ میشود، آن را زیر عدد ۱۰ مینویسیم و از آن کم میکنیم. حاصلش میشود ۲. اکنون آن عدد ۵ بالا را پایین میآوریم و در کنار ۲ قرار میدهیم. حال عدد ۲۵ را داریم. اکنون باید ۲۵ را بر ۸ تقسیم کنیم. حاصل این تقسیم ۳ است. ۳ را در کنار ۱ خارج قسمت مینویسیم.
در مرحله بعد یک عدد را حدس میزنیم که حاصلضرب آن در مقسوم علیه، یعنی عدد ۸، کمتر از عدد مقسوم، یعنی ۱۰۵، باشد.
عدد ۸ برای این کار مناسب است. اکنون ۸ را در مقسوم علیه ضرب میکنیم و حاصل (یعنی ۲۴) را زیر مقسوم مینویسیم. سپس ۲۴ را از ۲۵ کم میکنیم که حاصلش میشود ۱ و کوچکتر از مقسوم علیه است و اینجاست که تقسیم متوقف میشود.
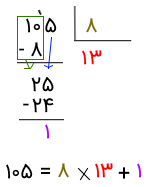
پس در این مثال، عدد ۱۰۵ مقسوم است، عدد ۸ مقسوم علیه، عدد ۱۳ خارج قسمت و عدد ۱ باقیمانده.
مقسوم علیه اول چیست ؟
در آموزش «اعداد اول — به زبان ساده (+ دانلود فیلم آموزش رایگان)» از مجله فرادرس با اعداد اول آشنا شدیم. دیدیم که عدد اول عددی است که فقط بر خودش و ۱ بخشپذیر است. دیدیم که اعداد ۲، ۳، ۵، ۷ و... اعداد اول بودند. مقسوم علیه اول یک عدد یعنی مقسومعلیههایی از عدد که اول باشند.
مقسوم علیه مشترک چیست ؟
مقسوم علیههای مشترک چند عدد، مقسوم علیهها یا عواملی هستند که در هر دو عدد مشترک باشند. بزرگترین مقسوم علیه مشترک نیز، همان گونه که از نامش پیداست، بزرگترین عدد بین مقسوم علیههای مشترک دو عدد است.
برای مثال، مقسوم علیههای دو عدد 12 و 30 را میتوان به صورت زیر فهرست کرد:
- مقسوم علیههای ۱۲: 1، 2، 3، 4، 6 و 12.
- مقسوم علیههای 30: 1، 2، 3، 5، 6، 10، 15 و 30.
مشاهده میکنیم که اعداد 1، 2، 3 و 6 در فهرست مقسوم علیههای هر دو عدد وجود دارند. در نتیجه، مقسوم علیههای مشترک 12 و 30، اعداد 1، 2، 3 و 6 هستند.
مثالها
در این بخش چند مثال را بررسی خواهیم کرد.
چند مثال از مقسوم
در ادامه، چند تقسیم را آوردهایم و میخواهیم مقسوم را در آن تعیین کنیم.
- الف) ۲ = ۱ ÷ ۲: در این تقسیم عدد ۲ مقسوم است.
- ب) ۲ = ۵ ÷ ۱۰: در این تقسیم عدد ۱۰ مقسوم است.
- ج) ۴ = 3 ÷ ۱۲: در اینجا ۱۲ مقسوم است.
- د) ۲۵ = 3 ÷ ۷۵: در این تقسیم ۷۵ مقسوم است.
پس باز هم توجه کنید که مقسوم آن عددی است که میخواهیم تقسیمش کنیم.
چند مثال از مقسوم علیه
در ادامه، میخواهیم چند مثال از مقسوم علیه را بررسی کنیم. موارد زیر را در نظر بگیرید:
- الف) ۵ = ۱۱ ÷ ۵۵: در این تقسیم ۱۱ مقسوم علیه است.
- ب) ۲ = ۱ ÷ ۲: در این تقسیم ۱ مقسوم علیه است.
- ج) ۲ = ۶ ÷ ۱۲: در این تقسیم ۶ مقسوم علیه است.
- د) ۳۰۰ = ۱ ÷ ۳۰۰: در این تقسیم ۱ مقسوم علیه است.
پس باز هم دیدیم که مقسوم علیه عددی است که مقسوم بر آن تقسیم شده است.
چند مثال از خارج قسمت
در این بخش، خارج قسمت چند تقسیم را با هم بررسی میکنیم.
- الف) ۱ = ۱۰۰ ÷ ۱۰۰: در این تقسیم ۱۱ خارج قسمت است.
- ب) ۲۳ = ۱ ÷ ۲۳: در این تقسیم ۱۱ خارج قسمت است.
- ج) ۲ = ۱۷ ÷ ۳۴: در این تقسیم ۱۱ خارج قسمت است.
- د) ۲ = ۳ ÷ ۶: در این تقسیم ۲ خارج قسمت است.
آزمون مقسوم و مقسوم علیه
۱. در یک تقسیم عدد صحیح، باقیمانده چه نقشی دارد و چه زمانی برابر صفر است؟
باقیمانده نشان میدهد عددی پس از تقسیم کامل باقی مانده و اگر تقسیم دقیق باشد، صفر است.
باقیمانده بیانگر تعداد دفعات تقسیم است و همیشه مثبت است.
باقیمانده فقط زمانی به دست میآید که مقسوم کوچکتر از مقسومعلیه باشد.
باقیمانده همیشه برابر با مقسومعلیه است و مقدارش عوض نمیشود.
باقیمانده عددی است که بعد از انجام تقسیم کامل، اگر عدد مقسوم به طور کامل بر مقسومعلیه بخشپذیر نباشد، باقی میماند. زمانی که تقسیم بدون باقیمانده انجام شود و عدد مقسوم به طور کامل به مقسومعلیه تقسیم شود، باقیمانده صفر میشود.
۲. رابطه بین ضرب و تقسیم در ریاضیات چگونه توصیف میشود و نمونهای از این رابطه چیست؟
تقسیم تنها برای اعداد اعشاری کاربرد دارد و ضرب فقط مخصوص اعداد صحیح است.
در تقسیم همیشه خارجقسمت برابر با یکی از اعداد ضرب است.
ضرب یک جمع تکراری است و تقسیم تفریق مکرر محسوب میشود و هر ضرب را میتوان با تقسیم معکوس کرد.
ضرب و تقسیم کاملا مستقل از یکدیگر هستند و هیچ ارتباطی ندارند.
در ریاضیات، ضرب به صورت جمع تکراری و تقسیم به عنوان تفریق مکرر شناخته میشود. این دو عملیات معکوس یکدیگرند، یعنی با انجام ضرب میتوان نتیجه تقسیم را بررسی کرد و بلعکس؛ برای مثال با ضرب کردن خارجقسمت و مقسومعلیه، دوباره به مقسوم میرسیم.
۳. برای پیدا کردن بزرگترین مقسومعلیه مشترک بین ۳۶ و ۴۸، کدام روش از نظر مفهوم تقسیم صحیح است و این عدد چه کمکی در حل مسائل تقسیم میکند؟
تمام مقسومعلیههای هر عدد را مشخص کرده و عوامل مشترک را بیابیم تا بزرگترین را انتخاب کنیم.
هر دو عدد را به عدد اول تقسیم کنیم و اولین عدد برابر را انتخاب کنیم.
عدد بزرگتر را بر عدد کوچکتر تقسیم کرده و باقیمانده را به عنوان بزرگترین مقسومعلیه مشترک در نظر بگیریم.
یکی از اعداد را فقط به عوامل فردی تقسیم کنیم و خارجقسمت میانگین را حساب کنیم.
برای به دست آوردن بزرگترین مقسومعلیه مشترک، باید مقسومعلیههای هر دو عدد را لیست کنیم و آنهایی که مشترک هستند را پیدا کنیم و بزرگترین آنها را انتخاب کنیم. این ویژگی به ویژه در تقسیمهای عددی اهمیت دارد، چون به ما کمک میکند سادهترین حالت تقسیم را تشخیص دهیم یا اعداد را به کوچکترین بخشهای برابر تقسیم کنیم.
