تبدیل عدد مخلوط به کسر — به زبان ساده + حل تمرین و مثال
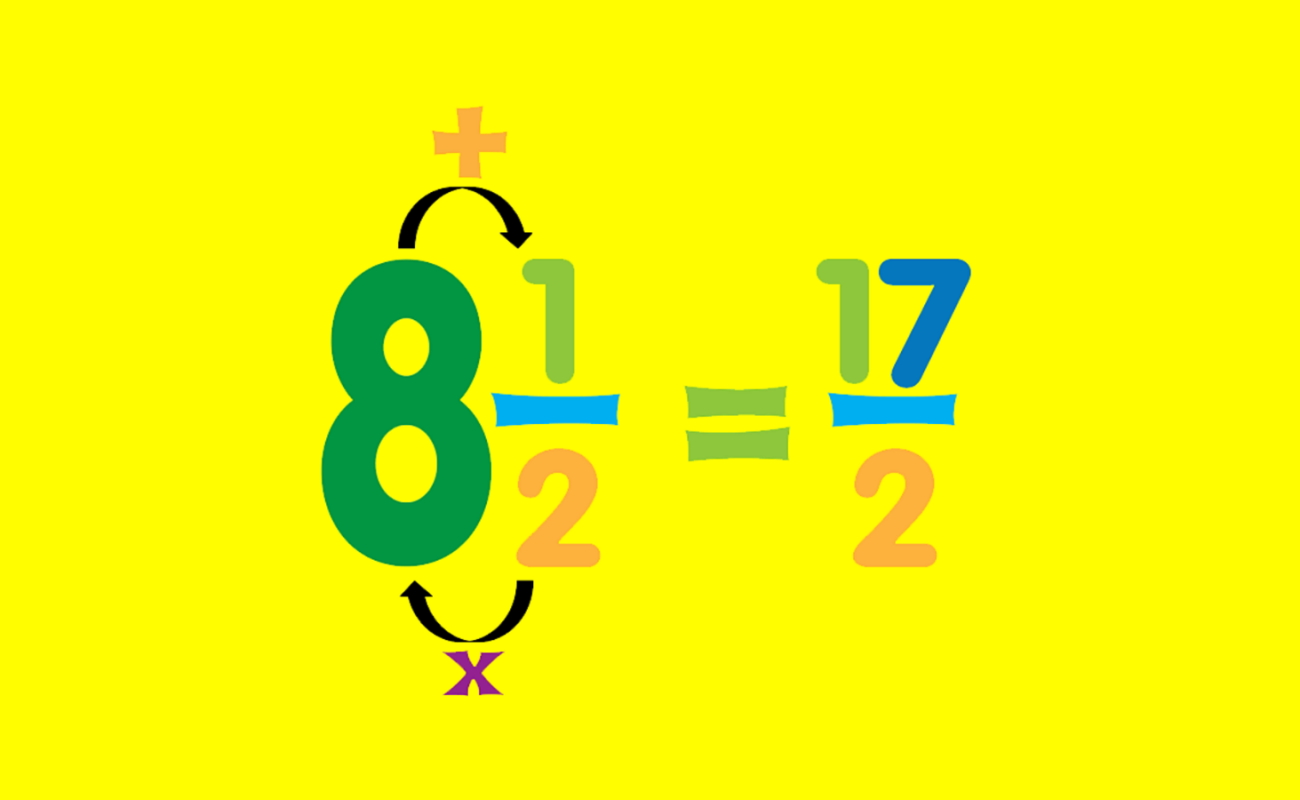
در آموزشهای پیشین مجله فرادرس، با اعداد مخلوط و کسرهای متعارفی آشنا شدیم. در این آموزش، میخواهیم ببینیم تبدیل عدد مخلوط به کسر چگونه انجام میشود.
عدد مخلوط چیست؟
عدد مخلوط عددی است که از یک عدد صحیح و یک کسر تشکیل شده است. برای مثال، عدد $$ 4 \frac 25 $$ یک عدد صحیح است که در آن، $$4$$ بخش صحیح و $$\frac 25 $$ بخش کسری این عدد است. اعداد زیر، همگی مخلوط هستند:
$$ \large \large 1 \frac 1 2 , \;\;20 \frac 56 , \; \; 6 \frac 19 $$
برای آشنایی بیشتر با اعداد مخلوط، به آموزشهای زیر مراجعه کنید:
- عدد مخلوط چیست و به چه اعدادی می گویند؟ — به زبان ساده
- جمع اعداد مخلوط — به زبان ساده + حل تمرین و مثال
- تفریق اعداد مخلوط — به زبان ساده + حل تمرین
روش تبدیل عدد مخلوط به کسر
اگر دقت کنید، عدد $$ 4 \frac 13 $$ را اینگونه میخوانیم: چهار و یکسوم ($$4$$ و $$\frac 13 $$). این دقیقاً همان مفهوم عدد مخلوط است که بیان میکند کسر $$ 4 \frac 13 $$ از جمع $$4 $$ و $$ \frac 13 $$ تشکیل شده است. این یعنی $$ 4\frac 13 = 4 + \frac 13 $$.
از همین مفهوم، برای تبدیل عدد مخلوط به کسر استفاده میکنیم. فرض کنید میخواهیم عدد مخلوط $$ 4 \frac 13 $$ را به کسر تبدیل کنیم. برای درک بهتر، مراحل را گام به گام طی میکنیم.
اول اینکه، میدانیم عدد مخلوط $$ 4 \frac 13 $$ را میتوان بهصورت مجموع زیر نوشت:
$$ \large 4\frac 13 = 4 + \frac 13 $$
همانطور که میبینیم، برای تبدیل عدد مخلوط به کسر، باید مجموع بالا را، که مجموع یک عدد صحیح و یک عدد کسری است، محاسبه کنیم. برای این کار، باید عدد $$ 4 $$ را بهشکل یک کسر هممخرج با $$ \frac 13 $$ بنویسیم (مخرج مشترک بگیریم). عدد $$ 4 $$ برابر با $$ \frac 41 $$ است. برای آنکه مخرج آن را به $$3$$ تبدیل کنیم، باید صورت و مخرجش را در عدد $$ 3 $$ ضرب کنیم:
$$ \large 4 = \frac 41 = \frac {4 \times 3 } { 1 \times 3 } = \frac { 1 2 } { 3 } $$
میبینیم که عدد کسری $$ \frac {12}{3}$$ معادل $$ 4 $$ است. بنابراین، خواهیم داشت:
$$ \large 4\frac 13 = 4 + \frac 13 = \frac {12 } { 3 } + \frac 13 = \frac { 13 } { 3 } $$
همانطور که مشخص است، بهراحتی توانستیم تبدیل عدد مخلوط به کسر را انجام دهیم.
یک مثال دیگر را بررسی میکنیم. میخواهیم عدد مخلوط $$ 10 \frac 47 $$ را به کسر تبدیل کنیم. ابتدا عدد مخلوط را اینگونه مینویسیم:
$$ \large 10 \frac 47 = 10 + \frac 4 7 $$
در گام بعدی، عدد $$10$$ را به کسر تبدیل میکنیم. برای این کار مخرج مشترک میگیریم:
$$ \large 10 + \frac 4 7 = \frac {10}{1} +\frac 47 = \frac {10\times 7} {1 \times 7}+ \frac 47 = \frac {70}{7}+\frac 47= \frac {70+4}{7}= \frac {74}{7}$$
یک روش سادهتر برای تبدیل عدد مخلوط به کسر
فرض کنید عدد مخلوط زیر را داشته باشیم.
$$ \large a \frac b c $$
که در آن، $$ a $$ عدد مربوط به بخش صحیح عدد مخلوط، $$ b $$ صورت کسر مربوط به بخش کسری عدد مخلوط و $$c $$ مخرج آن باشد. در این صورت، تبدیل عدد مخلوط به کسر اینگونه انجام میشود:
$$ \large a \frac b c = \frac { (a \times c) + b} {c } $$
دقت کنید که این روش ساده، از همان روش اصلی حاصل شده است.
اکنون یک مثال را بررسی میکنیم. فرض کنید میخواهیم عدد مخلوط $$ 10 \frac 5 {12}$$ را به کسر تبدیل کنیم. با توجه به فرمولی که بیان کردیم، خواهیم داشت:
$$ \large 10 \frac 5 {12} = \frac {(10 \times 12)+5}{12} = \frac {120+5}{12} = \frac {125}{12}$$
تبدیل عدد مخلوط به کسر با شکل
این روش را با یک مثال شرح میدهیم. فرض کنید میخواهیم عدد $$ 2 \frac 2 5 $$ را به کسر تبدیل کنیم. از مخرج کسر درمییابیم که باید شکلهایی داشته باشیم که به ۵ قسمت تقسیم شدهاند. برای نمایش عدد $$ 2 \frac 25 $$، دو شکل و دو بخش از یک شکل دیگر را رسم میکنیم. در اینجا از دایره استفاده کردهایم. بخشهای قرمز شکل زیر، عدد مخلوط $$ 2 \frac 25 $$ را نشان میدهند.
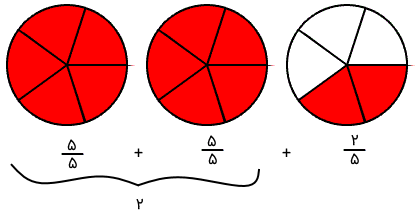
برای آنکه عدد مخلوط را به کسر تبدیل کنیم، ابتدا مخرج آن را تعیین میکنیم. مخرج همان مخرج بخش کسری عدد مخلوط، یعنی $$5$$ است. برای تعیین صورت کسر، کافی است تعداد تکههای قرمز را بشماریم که در اینجا $$ 5 + 5 + 2 = 12 $$ است. بنابراین، عدد مخلوط را میتوان بهشکل کسری زیر نوشت:
$$ \large 2 \frac 25 = \frac {12}{5} $$
مثالهای تبدیل عدد مخلوط به کسر
در این بخش، چند مثال را از تبدیل عدد مخلوط به کسر بررسی میکنیم.
مثال اول تبدیل عدد مخلوط به کسر
عدد $$ 1 \frac 12 $$ را به کسر تبدیل کنید.
حل: بهسادگی، میتوانیم این عدد مخلوط را به کسر تبدیل کنیم:
$$ \large 1 \frac 1 2 = \frac { ( 1 \times 2 ) + 1 } { 2 } = \frac { 2 + 1 } { 2 } = \frac 3 2 $$
مثال دوم تبدیل عدد مخلوط به کسر
عدد $$ 2 \frac 0 7 $$ را به کسر تبدیل کنید.
حل: این مثال را نیز مانند همان فرمولی که گفتیم، حل میکنیم. طبق فرمولی که گفتیم، در این مثال، $$ a = 2 $$، $$ b = 0 $$ و $$ c = 7 $$ است. بنابراین، خواهیم داشت:
$$ \large 2 \frac 0 7 = \frac { (2 \times 7 ) +0 } { 7 } = \frac {14+0}{7}= \frac { 14 } 7 $$
مثال سوم تبدیل عدد مخلوط به کسر
عدد مخلوط $$ 0 \frac 3 8 $$ را به کسر تبدیل کنید.
حل: با نگاهی به این عدد میبینیم که خودش یک کسر است، زیرا بخش صحیح آن صفر است. پس بهراحتی این عدد مخلوط بهشکل کسر زیر نوشته میشود:
$$ \large \frac 38 $$
اما اگر بخواهیم از روشی که گفتیم، استفاده کنیم، عدد مخلوط بهصورت زیر به کسر تبدیل میشود:
$$ \large 0 \frac 38 = \frac { (0 \times 8 ) + 3 } { 8 } = \frac { 0 + 3 } { 8 } = \frac 38 $$
مثال چهارم تبدیل عدد مخلوط به کسر
حاصل جمع $$ 1\frac 23 +1\frac 14 $$ را حساب کنید.
حل: ابتدا، دو عدد را بهصورت کسر مینویسیم:
$$ \large \begin {align} 1 \frac 2 3 + 1 \frac 1 4 &= ( \frac { 1 \times 3 } 3 + \frac 2 3 ) + ( \frac { 1 \times 4 } 4 +\frac 1 4 ) \\ &= \frac { 3 + 2 } { 3 } + \frac { 4 + 1 } { 4 } = \frac 53 + \frac 5 4
\end {align} $$
سپس، از آنجا که مخرجها متفاوت هستند، مخرج مشترک میگیریم. ک.م.م دو عدد $$3$$ و $$4$$، عدد $$12$$ است. جمع دو کسر بهصورت زیر خواهد بود:
$$\large \frac {5 \times 4}{3\times 4 }+ \frac {5 \times 3 }{4 \times 3 } = \frac {20}{12} + \frac {15}{12}= \frac {35}{12} $$
اکنون باید این کسر را به یک عدد مخلوط تبدیل کنیم:
$$ \large \begin {align} \frac {35} {12} = \frac {24+11}{12}= \frac {24}{12}+\frac {11}{12}=2+\frac {11}{12} = 2\frac {11}{12} \end {align} $$
مثال پنجم تبدیل عدد مخلوط به کسر
حاصل تفریق $$ 4 \frac 1 3 - 1 \frac 2 3 $$ را بهدست آورید.
حل: ابتدا دو عدد مخلوط را به کسر تبدیل میکنیم:
$$ \large \begin {align}
4 \frac 1 3 - 1 \frac 2 3 & = (\frac {4 \times 3 }{ 1 \times 3 }+ \frac 13 ) - (\frac {1 \times 3 }{1 \times 3 }+ \frac 23 )\\& = (\frac {12}{3} + \frac 13 ) - ( \frac 33 + \frac 23) \\ & = \frac {13}{3}- \frac {5}{3}
\end {align} $$
اکنون یک تفریق بین دو کسر داریم و بهسادگی میتوانیم آن را انجام دهیم:
$$ \large \begin {align}
\frac {13}{3}- \frac {5}{3} = \frac {13-5}{3}= \frac {8 }{ 5 }
\end {align} $$
اکنون میتوانیم این عدد کسری را بهشکل یک عدد مخلوط بنویسیم:
$$ \large \begin {align}
\frac {8 }{ 5 } = \frac { 5 + 3 } { 5 } = \frac 55 + \frac 35 = 1 + \frac 35 = 1 \frac 35
\end {align} $$
مثال ششم تبدیل عدد مخلوط به کسر
عدد $$ 5 \frac 23 $$ را به کسر تبدیل کنید.
حل: کسر بهصورت زیر محاسبه میشود:
$$ \large 5 \frac 23 = \frac { (5 \times 3 )+2}{3}=\frac {15+2}{3} = \frac { 17 } 3 $$
مثال هفتم تبدیل عدد مخلوط به کسر
عدد $$ 9 \frac 1 {10} $$ را به کسر تبدیل کنید.
حل: با استفاده از روشی که بیان کردیم، خواهیم داشت:
$$ \large 9 \frac 1 { 10 } = \frac { ( 9 \times 10 ) + 1 } { 10} = \frac { 90+1 } { 10} = \frac { 91} { 10 } $$
معرفی فیلم آموزش ریاضی پایه هفتم
برای آشنایی بیشتر با مباحث درس ریاضی پایه هفتم، پیشنهاد میکنیم فیلم آموزش ریاضی پایه هفتم فرادرس را مشاهده کنید که در ۱۳ ساعت و ۳ دقیقه تدوین شده و همه مباحث 14 درس کتاب درسی را بهطور کامل پوشش میدهد. در فصل یکم این آموزش، راهبردهای حل مسئله معرفی میشود. فصل دوم درباره عددهای صحیح است. فصل سوم درباره جبر و معادله است. در فصل چهارم به هندسه و استدلال پرداخته شده است. موضوع فصل ششم سطح و حجم است. در فصل هفتم به توان و جذر پرداخته شده است. فصل هشتم به بردار و مختصات اختصاص یافته است و در نهایت، آمار و احتمال در فصل نهم معرفی میشود.
- برای مشاهده فیلم آموزش ریاضی پایه هفتم + اینجا کلیک کنید.
جمعبندی
در این آموزش، با روش تبدیل اعداد مخلوط به کسر آشنا شدیم. روش تشریحی این کار را بیان کردیم و دیدیم که با استفاده از آن روش، بهراحتی میتوان با یک فرمول ساده، عدد مخلوط را به کسر تبدیل کرد. همچنین، مثالهای متنوعی را حل کردیم.










