تابع مختلط – به زبان ساده (+ دانلود فیلم آموزش رایگان)
در مطالب گذشته وبلاگ فرادرس در مورد اعداد حقیقی و مختلط صحبت شد. همانطور که احتمالا میدانید به رابطهای که روی اعداد حقیقی تعریف میشود بهطور ساده تابع گفته میشود. اما آیا تابعی وجود دارد که ورودیها و خروجیهای آن اعدادی مختلط باشد. در این مطلب قصد داریم تا نحوه بیان یک تابع مختلط را توضیح داده و مفهوم حد و مشتق را برای آن توضیح دهیم.
مقدمه
در این مطلب توابع مختلط را معرفی کرده و نحوه اعمال عملگرهایی همچون حد یا مشتق را در این توابع توضیح خواهیم داد. نمادهای استفاده شده برای یک تابع مختلط تقریبا مشابه با نمادهای یک تابع حقیقی است. در حقیقت بهشکلی ساده کافی است تا مقدار حقیقی را با مقدار مختلط جایگزین کنید. البته توجه داشته باشید که خروجی، مفهوم و کاربرد یک تابع مختلط نسبت به تابع حقیقی بسیار متفاوت است. بهطور دقیقتر میتوان گفت که یک تابع مختلط، خودش از دو تابع تشکیل شده است. تابع اول نشاندهنده بخش حقیقی و تابع دوم نشاندهنده قسمت موهومی خروجی است.
در کاربردهای مهندسی و علوم پایه موارد بسیاری پیش میآید که در آن یک حرکت متناوب با استفاده از دو تابع حقیقی توصیف میشود. اما مجموع این دو تابع حقیقی، تابعی مختلط را ایجاد میکنند که میتوان با در نظر گرفتن آن، پدیده فیزیکی را بهشکلی راحتتر توصیف کرد. خوب است بدانید شکل کلی یک پدیده فیزیکی متناوب، در معادلهای تحت عنوان معادله لاپلاس که در زیر آمده، توصیف میشود.
اگر بهجای در تابع فوق، دما () قرار بگیرد، توزیع آن در یک فضای دوبعدی بدست خواهد آمد.
تابع مختلط
بهمنظور تعریف تابع مختلط، در ابتدا متغیر مختلط را بر حسب دو متغیر حقیقی و مستقل و ، بهصورت زیر تعریف میکنیم.
توجه داشته باشید که مقادیر و ، حقیقی هستند. همچنین مقدار است. حال متغیر مختلط دوم یا را بهصورت زیر تعریف میکنیم.
مقادیر و را نیز حقیقی در نظر بگیرید. در این صورت مقدار مختلط میتواند تابعی از مقدار مختلط باشد. در حقیقت تابعی تحت عنوان هر نقطه از صفحه را به نقطهای در صفحه منتقل میکند. در این حالت، این وابستگی را میتوان بهشکل زیر بیان کرد:
برای نمونه تابعی بهصورت را در نظر بگیرید. این تابع به ازای تمامی مقادیر تعریف شده و با فرض ، رابطه برابر میشود با:
در نتیجه بخشهای حقیقی و موهومی نیز برابر میشوند با:
برای نمونه فرض کنید میخواهیم ورودی را برابر با انتخاب کنیم. در حقیقت در این حالت مقادیر و بهترتیب برابر با و انتخاب شدهاند. در این صورت خروجی برابر است با:
مثال ۱
- به ازای چه مقداری از تابع قابل تعریف است.
- در تابع تعریف شده در قسمت (a)، بخشهای را یافته و خروجی به ازای چقدر است؟
(a): بدیهی است که مخرج نمیتواند صفر باشد. از این رو تابع به ازای تمامی مقادیر بهغیر از قابل تعریف است.
(b): برای بدست آوردن و کافی است بخشهای حقیقی و موهومی را مطابق با عبارت زیر برابر با تابع قرار دهید.
در نتیجه بخشهای و برابرند با:
با توجه به بخشهای حقیقی و موهومی بدست آمده برای ، مقدار آن در نیز برابر است با:
حد تابع مختلط
حد تابع زمانی که میل میکند، برابر با است، اگر با نزدیک شدن به اندازه دلخواه به ، مقدار نیز به اندازهای دلخواه به صفر نزدیک شود. در برخی از موارد حاصل حد را میتوان بهراحتی و با محاسبه بدست آورد. برای نمونه حد تابع زمانی که میل میکند، برابر است با:
در مورد حد، تفاوتی بنیادین میان تابع حقیقی و تابع مختلط وجود دارد. در حقیقت روی نمودار میتوان از دو سمت چپ یا راست به یک نقطه مشخص نزدیک شد. این در حالی است که به منظور نزدیک شدن به نقطه در تابع ، مقدار باید به صفر نزدیک شود.
برای درک بهتر فرض کنید میخواهیم حاصل حد تابع را زمانی که است، بدست آوریم. بهمنظور محاسبه این حد میتوان از مسیرهایی مختلف به نقطه مذکور نزدیک شد. در شکل زیر این مسیرها نشان داده شدهاند.
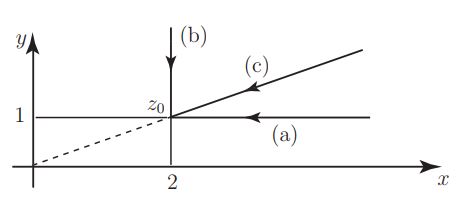
(a): در این مسیر، بوده و حد تابع برابر میشود با:
با جایگذاری مقادیر در عبارت بدست آمده در بالا، حاصل حد در این مسیر برابر است با:
(b): مسیر برابر با و حد تابع نیز برابر است با:
با جایگذاری مقادیر در رابطه فوق نیز، حاصل حد تابع برابر میشود با:
(c): همانطور که میبینید این مسیر بهصورت شیبدار به نزدیک شده است. با ترسیم خطی بین مبدا و نقطه میتوان دید که شیب خط برابر با ۳۰ درجه است. بنابراین مقدار در مقادیر مختلف برابر با است. در نتیجه حاصل حد برابر است با:
با جایگذاری نقطه در عبارت بدست آمده در بالا، حاصل حد از این مسیر، برابر با مقدار زیر بدست میآید.
همانطور که مشاهده میکنید هر سه مسیر نزدیک شده به نتیجهای مشابه را میدهند. از این رو بهنظر میرسد تابع در این نقطه حد دارد.
حال احتمالا این سوال را در ذهن داشته باشید که آیا تمامی توابع مختلط دارای حد در نقاط مختلف هستند؟ بدین منظور در ابتدا باید با معنی پیوستگی در یک تابع مختلط آشنا باشید. در ادامه پیوستگی در توابع مختلط توضیح داده شده است.
تعریف پیوستگی
تابع زمانی در پیوسته است که دو گزاره زیر برای آن برقرار باشد.
- موجود باشد.
- حد موجود بوده و مقدار آن برابر با باشد.
برای نمونه تابع مختلط را در نظر بگیرید. فرض کنید میخواهیم حد این تابع را زمانی که میل میکند، بدست آوریم. حد این تابع برابر با مقدار خود تابع در نقطه است. در نتیجه میتوان گفت:
در نتیجه حد تابع موجود بوده و برابر با مقدار تابع در نقطه است. از این رو تابع در این نقطه پیوسته است. اما مقادیر این تابع در دو نقطه موجود نیست (این مقادیر برابر با ریشههای مخرج هستند). از این رو تابع مختلط در این نقطه ناپیوسته است.
مشتق توابع مختلط
تابعی همچون زمانی در نقطه مشتقپذیر است که حاصل حد زیر موجود باشد.
توجه داشته باشید که مقدار برابر است با:
همانطور که میبینید تعریف مشتق در تابع مختلط بسیار مشابه با مشتق در تابع حقیقی است. تنها تفاوت در این است که در تابع مختلط، به جای از استفاده میشود. همچنین نماد مشتق در تابع مختلط به یکی از دو صورت زیر نشان داده میشود.
به نقطهای که در آن مشتق تابع وجود نداشته باشد، «نقطه تکین» (Singular Point) گفته میشود.
تابع تحلیلی
به تابع مختلط ، تحلیلی در نقطه گفته میشود، اگر مشتق آن در همسایگی موجود باشد. برای نمونه تابع زیر را در نظر بگیرید.
با صفر دادن مخرج داریم:
نقاط بدست آمده در بالا، نقاطی تکین محسوب میشوند. برای دیگر نقاط میتوان از قوانین معمول مشتق استفاده کرد و مشتق تابع مختلط را مطابق با رابطه زیر محاسبه کرد:
مثال ۲
نقاط تکین تابع مختلط زیر را بیابید. همچنین مشتق این تابع را در بدست آورید.
بدیهی است که این تابع در ریشههای مخرج مشتقپذیر نیست. از این رو میتوان مخرج را بهصورت زیر برابر با صفر قرار داده و محل نقاط تکین را بدست آورد.
نتیجه فوق نشان میدهد که مشتق تابع در نقطه موجود است. مقدار این مشتق نیز برابر است با:
با قرار دادن :
شاید برایتان جالب باشد که تابع در تمامی نقاط صفحه مختلط تحلیلی نیست. بهمنظور اثبات این موضوع از تعریف مشتق در نقطه مشخصی همچون استفاده میکنیم. مشتق تابع در نقطه فرضی برابر است با:
به منظور اثبات مشتقناپذیری تابع در نقطهای همچون ، باید حد نداشتن عبارت فوق را اثبات کنیم. بدین منظور در ابتدا موازی با محور به سمت نقطه حرکت میکنیم. در این حالت مقادیر تغییر نمیکنند. از این رو میتوان گفت:
در حالت دوم در راستای محور به سمت نقطه نزدیک میشویم. در این حالت نیز حاصل حد برابر میشود با:
همانطور که مشاهده میکنید در این حالت حاصل حد برابر با است. بنابراین از دو مسیر متفاوت، دو مقدار متفاوت بدست میآید. این امر نشان میدهد که حد مذکور دارای پاسخ نیست. در نتیجه تابع در نقطه تحلیلی نیست. در حقیقت این تابع در هیچ نقطهای از صفحه مختلط تحلیلی نیست.
در این مطلب مقدماتی در مورد تابع مختلط توضیح داده شد. همچنین مفاهیمی همچون حد، پیوستگی و مشتق را در این نوع از توابع توضیح دادیم. در مطالب آینده در مورد کاربردهای این تابع در محاسبه انتگرال روی مسیر بسته و محاسبه انتگرال صحبت خواهیم کرد.
در صورتی که مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی
- مجموعه آموزشهای فیزیک
- انتگرال — به زبان ساده
- مشتق — به زبان ساده
- حد در ریاضی -- به زبان ساده
^^













انشالله تو تک تک لحظه های زندگیت شاد باشی
بهترینارو براتون ارزو میکنم ک اینقدر قشنگ اموزش دادید🥹
عالی بود , مقایسه هایی که با تابع های حقیقی شده بود هم به درک موضوع کمک کرد.