کاربرد بهینه سازی در هندسه — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در هندسه، مسائل مختلفی وجود دارد که در آن‌ها می‌خواهیم بزرگترین یا کوچکترین مقدار یک تابع را پیدا کنیم. برای مثال، می‌توانیم محیط یا مساحت یک شکل یا حجم یک جسم را به عنوان یک تابع در نظر بگیریم. در این‌گونه مسائل بهینه سازی در هندسه می‌توانیم یکی از پارامترهای شکل یا جسم هندسی (مثلاً طول یک ضلع یا زاویه بین دو ضلع) را به عنوان یک متغیر مستقل در نظر بگیریم. بعد از تشکیل تابع، باید مقادیر اکسترمم را با استفاده از مشتق‌گیری پیدا کنیم. باید توجه کنیم که توابع چنین مسائلی معمولاً در یک بازه کراندار تعریف می‌شوند که با هندسه سیستم و یا شرایط مسئله تعیین می‌گردند.

مثال‌های بهینه سازی در هندسه

در این بخش، مثال‌های متنوعی را درباره کاربرد بهینه‌سازی در هندسه ارائه می‌کنیم.

مثال ۱

نقطه $$ A\left( {a,b} \right) $$ در ربع اول صفحه مختصات داده شده است. یک خط مستقیم رسم می‌کنیم که از این نقطه می‌گذرد و محورهای مختصات را در ربع اول قطع می‌کند. محل‌های برخورد با محورها را به گونه‌ای بیابید که مساحت مثلث تشکیل شده کمترین مقدار ممکن را داشته باشد (شکل ۱).

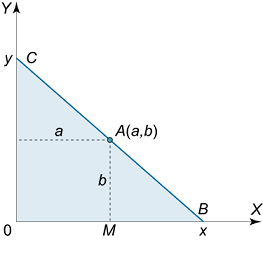
حل: مثلث‌های $$ OBC$$ و $$MBA$$ را در نظر می‌گیریم. این مثلث‌ها متشابه هستند. در نتیجه، رابطه زیر برقرار است:

$$ \large { \frac { { O C } } { { M A } } = \frac { { O B } }{ { M B } } \; \; } \kern0pt { \Rightarrow \; \; \frac { y } { b } = \frac { x } { { x – a } } } $$

که در آن، مختصات $$ x $$ و $$ y $$ در نامعادلات $$ x > a $$ و $$ y > b $$ صدق می‌کنند. با استفاده از معادله آخر می‌توانیم $$ y $$ را بر حسب $$ x $$ بیان کنیم:

$$ \large y = \frac { { b x } } { { x – a } } . $$

مساحت مثلث را با تابع $$ S\left( x \right) $$ بیان می‌کنیم:

$$ \large { S \left ( x \right ) = \frac { { x y } } { 2 } = \frac { x } { 2 } \cdot \frac { { b x } } { { x – a } } } = { \frac { { b { x ^ 2 } } } { { 2 \left ( { x – a } \right ) } } . } $$

مشتق تابع مساحت به صورت زیر است:

$$ \large \begin {align*}
S ’ \left ( x \right ) & = { \left ( { \frac { { b { x ^ 2 } } }{ { 2 \left ( { x – a } \right ) } } } \right ) ^ \prime } = { \frac { b } { 2 } { \left ( { \frac { { { x ^ 2 } } } { { x – a } } } \right ) ^ \prime } } = { \frac { b } { 2 } \cdot \frac { { 2 x \left ( { x – a } \right ) – { x ^ 2 } } } { { { { \left ( { x – a } \right ) } ^ 2 } } } } \\ & = { \frac { b } { 2 } \cdot \frac { { 2 { x ^ 2 } – 2 a x – { x ^ 2 } } } { { { { \left ( { x – a } \right ) } ^ 2 } } } } = { \frac { { b x \left ( { x – 2 a } \right ) } } { { { { 2 \left ( { x – a } \right ) } ^ 2 } } } . }
\end {align*} $$

تابع $$ S\left( x \right) $$ سه نقطه بحرانی $$ x = 0$$، $$ x = a $$ و $$ x = 2a $$ دارد. از آنجایی که $$ x > a $$ است، جواب نقطه $$ x = 2 a $$ است. وقتی از این نقطه بگذریم، علامت مشتق از منفی به مثبت تغییر می‌کند؛ یعنی $$ x = 2a $$ نقطه مینیمم تابع $$ S (x ) $$ است.

ارتفاع مثلث برابر است با:

$$ \large \require {cancel} y = \frac { { b x } } { { x – a } } = \frac { { b \cdot 2 a } } { { 2 a – a } } = \frac { { 2 \cancel { a } b } } { \cancel { a } } = 2 b . $$

بنابراین، برای آنکه مساحت مثلث، کوچکترین مقدار باشد، باید ساق‌های آن $$2a$$ و $$2b$$ باشند.

مثال ۲

یک ذوزنقه متساوی الساقین، درون دایره‌ای به شعاع $$R$$ محاط شده است (شکل ۲). زاویه $$\alpha $$ باید چقدر باشد تا مساحت ناحیه سایه زده شده حداقل شود؟

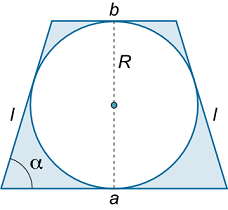
حل: مساحت یک ذوزنقه متساوی الساقین، با رابطه زیر به دست می‌آید:

$$ \large  { S _ T } = \frac { { a + b } } { 2 } \cdot h $$

که در آن، $$a$$ و $$b$$ قاعده‌ها و $$h$$ ارتفاع ذوزنقه هستند. واضح است که $$h = 2 R$$. مساحت دایره برابر با $$ {S_K} = \pi {R^2} $$ است. در نتیجه، مساحت ناحیه سایه زده شده به صورت زیر است:

$$ \large { S = { S _ T } – { S _ K } } = { \frac { { a + b } } { 2 } \cdot 2 R – \pi { R ^ 2 } } = { \left ( { a + b } \right ) R – \pi { R ^ 2 } . } $$

از آنجایی که ذوزنقه توسط دایره محاط شده است، مجموع دو ساق کناری برابر با مجموع قاعده‌ها است:

$$ \large { a + b = 2 \ell \; \; \text {or} \; \; } \kern0pt { a + b = 2 \cdot \frac { { 2 R } } { { \sin \alpha } } } = { \frac { { 4 R } } { { \sin \alpha } } . } $$

که در آن، $$l$$ ساق ذوزنقه را نشان می‌دهد. با جایگذاری $$\left( {a + b} \right)$$ در رابطه قبلی، داریم:

$$ \large {S = S\left( \alpha \right) = \frac{{4R}}{{\sin \alpha }} \cdot R – \pi {R^2} } = {{R^2}\left( {\frac{4}{{\sin \alpha }} – \pi } \right).} $$

اکنون مشتق $$ S\left( \alpha \right) $$ را برای محاسبه مقدار اکسترمم آن محاسبه می‌کنیم:

$$ \large \begin {align*} S’ \left ( \alpha \right ) & = { \left [ { { R ^ 2 } \left ( { \frac { 4 } { { \sin \alpha } } – \pi } \right ) } \right ] ^ \prime } \\ & = { 4 { R ^ 2 } \left ( { – \frac { 1 } { { { { \sin } ^ 2 } \alpha } } } \right ) \cdot \cos \alpha } = { – \frac { { 4 { R ^ 2 } \cos \alpha } } { { { { \sin } ^ 2 } \alpha } } . } \end {align*}$$

مشتق فوق، در حالت زیر برابر با صفر است:

$$ \large \cos \alpha = 0 , \; \; \Rightarrow \alpha = \frac { \pi }{ 2 } $$

وقتی از این نقطه عبور کنیم (زاویه زیاد شود)، مشتق از منفی به مثبت تغییر خواهد کرد. در نتیجه، $$ \alpha = \large\frac{\pi }{2}\normalsize$$‌ زاویه‌ای است که در آن، تابع $$ S\left( \alpha \right)$$ حداقل می‌شود. در این حالت، ذوزنقه به مربع تبدیل می‌شود. حداقل مقدار مساحت برابر است با:

$$ \large { S _ { \min } } = { R ^ 2 } \left ( { 4 – \pi } \right ) . $$

مثال ۳

پنجره‌ای از یک مستطیل و نیم‌دایره تشکیل شده است (شکل ۳). محیط پنجره برابر با $$P$$ است. شعاع $$R$$ نیم‌‌دایره را برای حالتی تعیین کنید که بیشترین مقدار نور از پنجره وارد شود.

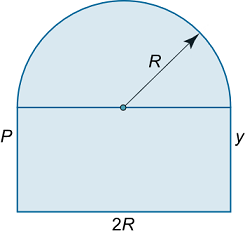
حل: واضح است که یک ضلع مستطیل برابر با $$2R$$ است. ضلع دیگر را با $$y$$ مشخص می‌کنیم. محیط پنجره برابر است با:

$$ \large P = \pi R + 2 R + 2 y . $$

از رابطه بالا، $$y$$ به صورت زیر به دست می‌آید:

$$ \large y = \frac { 1 } { 2 } \left [ { P – \left ( { \pi + 2 } \right ) R } \right ] . $$

مساحت پنجره نیز برابر است با:

$$ \large \begin {align*}
S & = \frac { { \pi { R ^ 2 } } } { 2 } + 2 R y = { \frac { { \pi { R ^ 2 } } } { 2 } + 2 R \cdot \frac { 1 } { 2 } \left [ { P – \left ( { \pi + 2 } \right ) R } \right ] } \\ & = { \frac { { \pi { R ^ 2 } } } { 2 } + P R – \pi { R ^ 2 } – 2 { R ^ 2 } } = { P R – \frac { { \pi { R ^ 2 } } } { 2 } – 2 { R ^ 2 } . }
\end {align*} $$

مساحت فوق، تابعی به صورت $$ S\left( R \right) $$ است. برای محاسبه مقدار اکسترمم این تابع، از آن مشتق می‌گیریم:

$$ \large \begin {align*} S’ \left ( R \right) & = \left ( P R – \frac { { \pi { R ^ 2 } } } { 2 } – 2 { R ^ 2 } \right ) ^ \prime \\ & = P – \pi R – 4 R = P – \left ( { \pi + 4 } \right ) R . \end {align*} $$

با صفر قرار دادن مشتق، داریم:‌

$$ \large { S’ \left ( R \right ) = 0 , \; \; } \Rightarrow { P – \left ( { \pi + 4 } \right ) R = 0 , \; \; } \Rightarrow { R = \frac { P } { { \pi + 4 } } . } $$

مشتق دوم، منفی است:

$$ \large { S ^ { \prime \prime } \left ( R \right ) = { \left [ { P – \left ( { \pi + 4 } \right ) R } \right ] ^ \prime } } = { – \left ( { \pi + 4 } \right ) \lt 0 } $$

در نتیجه، در نقطه‌ای که به دست آوردیم، مساحت حداکثر است. این مقدار ماکزیمم برابر است با:

$$ \large \begin {align*}
{ S _ { \max } } & = P R – \frac { { \pi { R ^2 } } } { 2 } – 2 { R ^ 2 } = { P \left ( { \frac { P } { { \pi + 4 } } } \right ) – \left ( { \frac { \pi } { 2 } + 2 } \right ) { \left ( { \frac { P } { { \pi + 4 } } } \right ) ^ 2 } } \\ & = { \frac { { { P ^ 2 } } }{ { \pi + 4 } } – \frac { { \left ( { \cancel { \pi + 4 } } \right ){ P ^ 2 } } } { { 2 { { \left ( { \pi + 4 } \right ) } ^ { \cancel { 2 } } } } } } = { \frac { { 2 { P ^ 2 } – { P ^ 2 } } } { { 2 \left ( { \pi + 4 } \right ) } } } = { \frac { { { P ^ 2 } } } { { 2 \left ( { \pi + 4 } \right ) } } . }
\end {align*} $$

مثال ۴

مستطیلی با اضلاع موازی با محورهای مختصات را در نظر بگیرید که یک ضلع آن روی محور $$x$$ قرار گرفته است و ضلع روبه‌رو توسط سهمی $$ y = c – {x^2} $$ محاط شده است. بزرگترین مساحت ممکن مستطیل را به دست آورید.

حل: فرض کنید نقطه $$ M\left( {x,y} \right) $$ رأس مستطیل باشد که متعلق به سهمی است (شکل ۴).

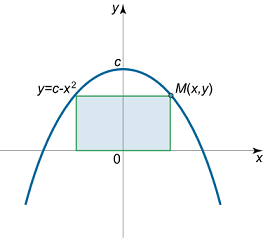
طول اضلاع مستطیل، $$2x$$ و $$2y$$ است. مساحت مستطیل برابر است با:

$$ \large { S \left ( x \right ) = 2 x y } = { 2 x \left ( { c – { x ^ 2 } } \right ) } = { 2 c x – 2 { x ^ 3 } . } $$

برای یافتن نقطه اکسترمم، از $$S(x)$$ مشتق می‌گیریم:

$$ \large S’ \left ( x \right ) = { \left ( { 2 c x – 2 { x ^ 3 } } \right ) ^ \prime } = 2 c – 6 { x ^ 2 } . $$

با برابر قرار دادن مشتق با صفر، داریم:

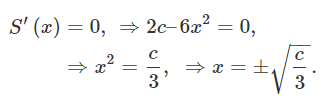
واضح است که هر دو ریشه، منجر به یک مقدار مساحت برابر خواهند شد. باید مطمئن شویم $$ \sqrt {\large\frac{c}{3}\normalsize} $$ یک نقطه ماکزیمم برای $$S(x)$$ است. این کار را با بررسی مشتق دوم انجام می‌دهیم:

$$ \large S ^ { \prime \prime } \left ( x \right ) = { \left ( { 2 c – 6 { x ^ 2 } } \right ) ^ \prime } = – 1 2 x \lt 0 . $$

از آنجایی که $$ S^{\prime\prime}\left( x \right) \lt 0 $$، نقطه $$ \sqrt {\large\frac{c}{3}\normalsize} $$ ماکزیمم است.

حداکثر مساحت مستطیل، برابر است با:

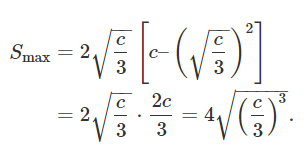
مثال ۵

دو کانال با عرض‌های $$a$$ و $$b$$ با زاویه قائم به یکدیگر متصل شده‌اند (شکل ۵). حداکثر طول یک کشتی را به گونه‌ای حساب کنید که در دو کانال قرار بگیرد.

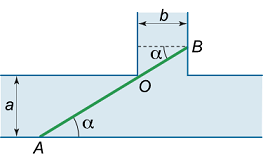
فرض می‌کنیم موقعیت کشتی، مطابق شکل ۵ با زاویه $$\alpha $$ تعیین شده باشد. حداکثر مقدار ممکن طول $$L$$ به زاویه $$ \alpha $$ بستگی دارد:

$$ \large { L = \left | { A O } \right | + \left | { O B } \right | } = { \frac { a } { { \sin \alpha } } + \frac { a } { { \cos \alpha } } } = { L \left ( \alpha \right ) . } $$

دو موقعیت اکسترمم به صورت زیر هستند:

$$ \large { \alpha \to 0 , \; \; } \Rightarrow { \sin \alpha \to 0 , \; \; } \Rightarrow { \left | { A O } \right | \to \infty ; } $$

$$ \large { \alpha \to \frac { \pi } { 2 } , \; \; } \Rightarrow { \cos \alpha \to 0 , \; \; } \Rightarrow { \left | { O B } \right | \to \infty . } $$

در نتیجه، زاویه $$ \alpha$$ در محدوده $$ 0 \lt \alpha \lt \large\frac{\pi }{2}\normalsize $$ تغییر می‌کند.

اکنون مشتق تابع $$ L\left( \alpha \right) $$ را به دست می‌آوریم:

$$ \large \begin {align*}
L’ \left ( \alpha \right ) & = \left ( { – \frac { a } { { { { \sin } ^ 2 } \alpha } } } \right ) \cdot \cos \alpha – \frac { b } { { { { \cos } ^ 2 } \alpha } } \cdot \left ( { – \sin \alpha } \right ) \\ & = { \frac { { b \sin \alpha } } { { { { \cos } ^ 2 } \alpha } } – \frac { { a \cos \alpha } } { { { \sin ^ 2 } \alpha } } } = { \frac { { b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha } }{ { { { \cos } ^ 2 } \alpha \, { { \sin } ^ 2 } \alpha } } } \\ & = { \frac { { 4 \left ( { b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha } \right ) } } { { { { \sin } ^ 2 } \left ( { 2 \alpha } \right ) } } . }
\end {align*} $$

با صفر قرار دادن رابطه اخیر، داریم:

$$ \large \begin {align*}
L’ \left ( \alpha \right ) & = 0 , \; \; \Rightarrow
{ \frac { { 4 \left ( { b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha } \right ) } } { { { { \sin } ^ 2 } \left ( { 2 \alpha } \right ) } } = 0 , \; \; } \\ & \Rightarrow
{ \left\{ { \begin {array} { * { 20 } { l } }
{ b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha = 0 } \\
{ { { \sin } ^ 2 } \left ( { 2 \alpha } \right ) \ne 0 }
\end {array} } \right. , \; \; }\\ & \Rightarrow
{ b \, { \tan ^ 3 } \alpha – a = 0, \; \; } \Rightarrow
{ \tan \alpha = \sqrt [ \large 3 \normalsize ] { { \frac { a }{ b } } } . }
\end {align*} $$

باید مطمئن شویم که وقتی از نقطه بحرانی $$ \alpha $$ می‌گذریم، علامت مشتق از منفی به مثبت تغییر می‌کند؛ یعنی مقدار مینیمم تابع $$ L ( \alpha )$$ در این نقطه رخ می‌دهد. معادلات سینوس و کسینوس $$\alpha $$ را بر حسب تانژانت می‌نویسیم:

$$ \large \begin {align*}
1 + { \cot ^ 2 } \alpha & = \frac { 1 } { { { { \sin } ^ 2 } \alpha } } , \; \; \\ \Rightarrow \sin \alpha & = \frac { 1 } { { \sqrt { 1 + { { \cot } ^ 2 } \alpha } }} \\ & = { \frac { 1 } { { \sqrt { 1 + \frac { 1 } { { { { \tan } ^ 2 } \alpha } } } } } } = { \frac { { \tan \alpha } } { { \sqrt { 1 + { { \tan } ^ 2 } \alpha } } } }
\end {align*} $$

$$ \large \begin {align*}
{ 1 + { \tan ^ 2 } \alpha = \frac { 1 } { { { \cos ^ 2 } \alpha } } , \; \; } \Rightarrow { \cos \alpha = \frac { 1 } { { \sqrt { 1 + { { \tan } ^ 2 } \alpha } } } . }
\end {align*} $$

اکنون می‌توانیم توصیف نهایی حداکثر طول ممکن کشتی را بنویسیم:‌

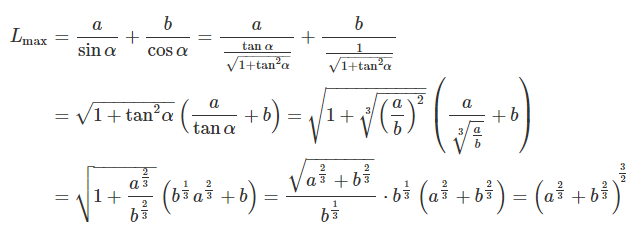
در یک حالت خاص، برای کانال‌هایی با عرض برابر ($$ a = b$$)، داریم:

$$ \large \begin {align*}
{ { L _ { \max } } = \sqrt { { { \left ( { 2 { a ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ) } ^ 3 } } } = { \sqrt { 8 { a ^ 2 } } = a \sqrt 8 . }
\end {align*} $$

مثال ۶

مستطیلی دارای اضلاعی موازی با محورهای مختصات است و درون یک بیضی محاط شده است (شکل ۶). معادله بیضی به صورت زیر است:

$$ \large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 $$

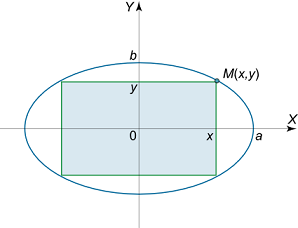
فرض کنید نقطه $$ M\left( {x,y} \right) $$، یک رأس مستطیل محاطی باشد. مساحت مستطیل برابر است با:

$$ \large S = 2 x \cdot 2 y = 4 x y . $$

کمیت $$y$$ را می‌توان از معادله بیضی به دست آورد:

$$ \large \begin {align*}
\frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } & = 1 , \; \; \Rightarrow { \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 – \frac { { { x ^ 2 } } } { { { a ^ 2 } } } , \; \; } \\ & \Rightarrow { { y ^ 2 } = \frac { { { b ^ 2 } } } { { { a ^ 2 } } } \left ( { { a ^ 2 } – { x ^ 2 } } \right ) , \; \; } \\ & \Rightarrow { y = \pm \frac { b } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } . }
\end {align*} $$

در این مسئله، فقط مقادیر مثبت $$x$$ و $$y $$ را در نظر می‌گیریم:

$$ \large { S = 4 x y } = { \frac {{ 4 b x } } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } } = { S \left ( x \right ) . } $$

برای یافتن اکسترمم، مشتق $$S(x)$$ را محاسبه می‌کنیم:

$$ \large \begin {align*}
S’ \left ( x \right ) & = { \left ( { \frac { { 4 b x } } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } } \right ) ^ \prime } = { \frac { { 4 b } } { a } \cdot } \kern0pt { \left [ { \sqrt { { a ^ 2 } – { x ^ 2 } } + x \cdot \frac { 1 } { { 2 \sqrt { { a ^ 2 } – { x ^ 2 } } } } \cdot \left ( { – 2 x } \right ) } \right ] } \\ & = { \frac { { 4 b } } { a } \left [ { \sqrt { { a ^ 2 } – { x ^ 2 } } – \frac { { { x ^ 2 } } } { { \sqrt { { a ^ 2 } – { x ^ 2 } } } } } \right ] } = { \frac { { 4 b } } { a } \cdot \frac { { { a ^ 2 } – { x ^ 2 } – { x ^ 2 } } } { { \sqrt { { a ^ 2 } – { x ^ 2 } } } } } = { \frac { { 4 b \left ( { { a ^ 2 } – 2 { x ^ 2 } } \right ) } } { { a \sqrt { { a ^ 2 } – { x ^ 2 } } } } . }
\end {align*} $$

اگر مشتق بالا را برابر با صفر قرار دهیم، داریم:

$$ \large { { a ^ 2 } – 2 { x ^ 2 } = 0 , \; \; } \Rightarrow { { x ^ 2 } = \frac { { { a ^ 2 } } } { 2 } , \; \; } \Rightarrow { x = \frac { a } { { \sqrt 2 } } . } $$

وقتی از نقطه $$ x = {\large\frac{a}{{\sqrt 2 }}\normalsize} $$ عبور می‌کنیم، علامت مشتق از مثبت به منفی تغییر می‌کند. بنابراین، ماکزیمم تابع در این نقطه رخ می‌دهد.

در نتیجه، مقدار $$y$$ برابر است با:

$$ \large \begin {align*}
y & = \frac { b } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } = { \frac { b } { a } \sqrt { { a ^ 2 } – { { \left ( { \frac { a } { { \sqrt 2 } } } \right ) } ^ 2 } } } \\ &= { \frac { b } { a } \sqrt { { a ^ 2 } – \frac { { { a ^ 2 } } } { 2 } } } = { \frac { b } { a } \sqrt { \frac { { { a ^ 2 } } } { 2 } } } = { \frac { b } { a } \cdot \frac { a } { { \sqrt 2 } } } = { \frac { b } { { \sqrt 2 } } . }
\end {align*} $$

بنابراین، مستطیل محاط شده در بیضی، وقتی بیشترین مساحت ممکن را خواهد داشت که اضلاع آن به صورت زیر باشند:‌

$$ \large \begin {align*}
{ 2 x = 2 \cdot \frac { a } { { \sqrt 2 } } = a \sqrt 2 \; \text{, } \; \; \; \; } \kern-0.3pt { 2 y = 2 \cdot \frac { b } { { \sqrt 2 } } = b \sqrt 2 . }
\end {align*} $$

حداکثر مقدار مساحت نیز برابر است با:‌

$$ \large { S _ { \max } } = a \sqrt 2 \cdot b \sqrt 2 = 2 a b . $$

در حالت خاصی که محورهای بزرگ و کوچک بیضی برابر باشند ($$ a = b = R $$)، با یک دایره مواجه خواهیم بود.

در این حالت، بزرگترین مساحت مستطیل، برابر است با:

$$ \large R \sqrt 2 $$

مثال ۷

تابلویی به ارتفاع $$a$$ روی یک دیوار به گونه‌ای آویزان شده است که به اندازه $$h$$ بالاتر از سطح چشم ناظر قرار دارد. فاصله چشم ناظر تا دیوار ($$x$$) باید چه مقداری باشد تا او تصویر را در مطلوب‌ترین حالت ممکن ببیند (شکل ۷ (الف))؟.

حل: واضح است که وقتی ناظر در وضعیت بهینه قرار دارد که، زاویه دید او حداکثر مقدار ممکن باشد.

ابتدا رابطه زاویه دید $$ \varphi = \angle BPA $$ را به دست می‌آوریم.

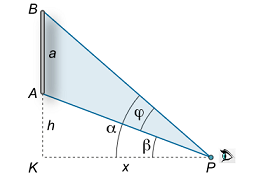
طبق شکل ۷ (ب)، رابطه $$ \varphi = \alpha – \beta $$ برقرار است که در آن:

$$ \large { \tan \beta = \frac { h } { x } , } \; \; \; \kern-0.3pt { \tan \alpha = \frac { { a + h } } { x } . } $$

با استفاده از اتحاد تانژانتِ تفاضلِ زاویه‌ها داریم:

$$ \large \begin {align*}
\require {cancel} \tan \varphi & = \tan \left ( {\alpha – \beta } \right ) = { \frac { { \tan \alpha – \tan \beta } } {{ 1 + \tan \alpha \tan \beta } } } \\
& = { \frac { { \frac { { a + h } } { x } – \frac { h } { x } } } { { 1 + \frac { { a + h } } { x } \cdot \frac { h } { x } } } } = { \frac { { \frac { { a + \cancel { h } – \cancel { h } } } { x } } } { { \frac { { { x ^ 2 } + \left ( { a + h } \right ) h } } { { { x ^ 2 } } } } } } \\& = { \frac { { a x } } { { {x ^ 2 } + a h + { h ^ 2 } } } . }
\end {align*} $$

بنابراین، می‌توانیم عبارت زیر را برای تابع $$ \varphi \left( x \right) $$ بنویسیم:

$$ \large { \varphi = \varphi \left ( x \right ) } = { \arctan \frac { { a x } } { { { x ^ 2 } + a h + { h ^ 2 } } } . } $$

مشتق این تابع برابر است با:

$$ \large \begin {align*}
\varphi ^ \prime \left ( x \right ) & = { \left ( { \arctan \frac { { a x } } { { { x ^ 2 } + a h + { h ^ 2 } } } } \right ) ^ \prime } = { \frac { 1 } { { 1 + { { \left ( { \frac { { a x } }{ { { x ^ 2 } + a h + { h ^ 2 } } } } \right ) } ^ 2 } } } \cdot { \left ( { \frac { { a x } } { { { x ^ 2 } + a h + { h ^ 2 } } } } \right ) ^ \prime } } \\ &= { \frac { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { { \left ( { a x } \right ) } ^ 2 } } } }\kern0pt { \cdot \frac { { a \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) – a x \cdot 2 x } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { { \left ( { a x } \right ) } ^ 2 } } } } \\ & = { \frac { { a { x ^ 2 } + { a ^ 2 } h + a { h ^ 2 } – 2 a { x ^ 2 } } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 } { x ^ 2 } } } } = { \frac { { { a ^ 2 } h + a { h ^2 } – a { x ^ 2 } } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 } { x ^ 2 } } } } \\ &= { \frac { { a \left ( { a h + { h ^ 2 } – { x ^ 2 } } \right ) } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 } { x ^ 2 } } } . }
\end {align*} $$

با صفر قرار دادن مشتق تابع بالا، داریم:

$$ \large \begin {align*}
\varphi ^ \prime \left ( x \right ) = 0 , \; \; & \Rightarrow { \frac { { a \left ( { a h + { h ^ 2 } – { x ^ 2 } } \right ) } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 }{ x ^ 2 } } } = 0 , \; \; } \\ & \Rightarrow { a h + { h ^ 2 } – { x ^ 2 } = 0 , \; \; } \\ & \Rightarrow { { x ^ 2 } = a h + { h ^ 2 } , \; \; } \Rightarrow { x = \sqrt { h \left ( { a + h } \right ) } .}
\end {align*} $$

در این نقطه، $$ \varphi \left( x \right) $$ مقدار ماکزیمم را دارد، زیرا وقتی از این نقطه می‌گذریم، مشتق اول، از مثبت به منفی تغییر علامت می‌دهد.

بنابراین، فاصله بهینه از دیوار برای بهترین زاویه دید از تصویر، با فرمول زیر به دست می‌آید:

$$ \large x = \sqrt { h \left ( { a + h } \right ) } . $$

برای مثال، اگر $$a = 3\,\text{m} $$ و $$h = 2\,\text{m} $$ باشد، فاصله بهینه برابر خواهد بود با:

$$ \large { x = \sqrt { h \left ( { a + h } \right ) } = \sqrt { 2 \left ( { 3 + 2 } \right ) } } = { \sqrt { 1 0 } \approx 3 . 1 6 \, \text {m} . } $$

مثال ۸

دو ضلع یک متوازی الاضلاع و یک رأس آن بر یک مثلث منطبق شده‌اند (شکل ۸). در چه شرایطی مساحت این متوازی الاضلاع حداکثر مقدار ممکن است؟

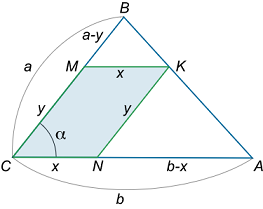
حل: مثلث را با دو ضلع $$ a = BC $$ و $$ b = AC $$ و زاویه $$ \alpha = \angle BCA $$ بین آن‌ها تعریف می‌کنیم. متوازی الاضلاع $$ CMKN $$ را طبق شرایط مسئله رسم می‌کنیم. اضلاع متوازی الاضلاع را به صورت $$ x = MK $$ و $$ y = KN $$ در نظر می‌گیریم. مساحت متوازی الاضلاع با فرمول زیر تعیین می‌شود:

$$ \large S = xy\sin \alpha . $$

پارامتر $$y$$ را بر حسب $$x$$ و اضلاع $$a$$ و $$b$$ مثلث می‌نویسیم.

با توجه به تشابه مثلث‌های $$ BMK $$ و $$ BCA $$، داریم:

$$ \large \frac { { a – y } } { a } = \frac { x } { b } . $$

در نتیجه، می‌توان نوشت:

$$ \large \begin {align*}
\left ( { a – y } \right ) b & = a x , \; \; \Rightarrow { a b – b y = a x , \; \; } \Rightarrow { b y = a b – a x , \; \; } \\ & \Rightarrow { y = \frac { { a b – a x } } { b } = a – \frac { a } { b } x . }
\end {align*} $$

در نتیجه، مساحت $$S$$ را می‌توان به صورت تابع $$S(x)$$ نوشت:

$$ \large \begin {align*}
S & = S \left ( x \right ) = { x \left ( { a – \frac { a } { b } x } \right ) \sin \alpha } \\ & = { a x \sin \alpha – \frac { a } { b }{ x ^ 2 } \sin \alpha . }
\end {align*} $$

وقتی از این نقطه عبور می‌کنیم، مشتق از مثبت به منفی تغییر علامت می‌دهد و بنابراین، در آن، مقدار تابع حداکثر است. ضلع دیگر متوازی الاضلاع برابر است با:

$$ \large \begin {align*}
{ y = a – \frac { a } { b } x = a – \frac { a } { b } \cdot \frac { b } { 2 } } = { a – \frac { a } { 2 } = \frac { a } { 2 } . }
\end {align*} $$

بنابراین، متوازی الاضلاع با ضلع‌های $$x$$ و $$y$$ که در مثلث محاط شده است، در شرایط زیر بیشترین مساحت را خواهد داشت:

$$ \large x = \frac { b } { 2 } , \; \; y = \frac { a } { 2 } $$

مثال ۹

استوانه‌ای را پیشنهاد دهید که مساحت سطح آن حداقل باشد.

حل: شکل بهینه یک استوانه با حجم ثابت، هزینه مواد به کار رفته در آن را کاهش می‌دهد. این مسئله در موارد مختلفی مانند مخزن‌های ذخیره نفت مهم است (شکل ۹).

فرض می‌کنیم $$H$$ ارتفاع استوانه و $$R$$ شعاع سطح مقطع آن است. حجم و مساحت کل سطح استوانه با فرمول‌های زیر بیان می‌شود:

$$ \large { V = \pi { R ^ 2 } H , } \; \; \; \kern-0.3pt { S = 2 \pi { R ^ 2 } + 2 \pi R H . } $$

شعاع قاعده $$R$$ را به عنوان یک متغیر مستقل در نظر می‌گیریم و ارتفاع $$H$$ را بر حسب آن می‌نویسیم (در حجم ثابت $$V$$):

$$ \large H = \frac { V } { { \pi { R ^ 2 } } } . $$

می‌خواهیم مقدار اکسترمم تابع مساحت سطح $$S(R)$$ را محاسبه کنیم:‌

$$ \large \begin {align*}
S \left ( R \right ) & = 2 \pi { R ^ 2 } + 2 \pi R H \\ &= { 2 \pi { R ^ 2 } + 2 \pi R \cdot \frac { V } { { \pi { R ^ 2 } } } } \\ & = { 2 \pi { R ^ 2 } + \frac { { 2 V } } { R } . }
\end {align*} $$

مشتق تابع بالا برابر است با:

$$ \large { S’ \left ( R \right ) = { \left ( { 2 \pi { R ^ 2 } + \frac { { 2 V } } { R } } \right ) ^ \prime } } = { 4 \pi R – \frac {{ 2 V } } { { { R ^ 2 } } } } = { \frac { { 4 \pi { R ^ 3 } – 2 V } } { { { R ^ 2 } } } . } $$

با صفر قرار دادن این مشتق، داریم:

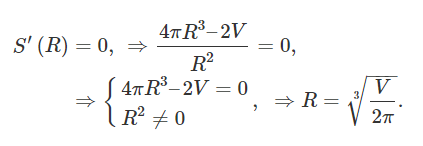
مقدار $$R$$ بالا، متناظر با حداقل مساحت سطح $$S(R)$$ است، زیرا با عبور از این نقطه، علامت مشتق از منفی به مثبت تغییر می‌کند.

در نتیجه، ارتفاع استوانه برابر خواهد بود با:

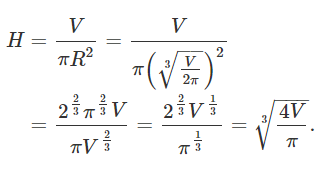
نسبت ارتفاع به شعاع قاعده، به صورت زیر است:

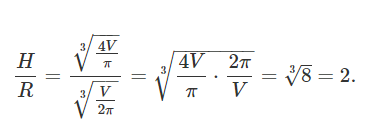
به عبارت دیگر، برای آنکه مساحت جانبی استوانه کوچکترین مقدار ممکن شود، باید ارتفاع آن برابر با قطر قاعده باشد.

مثال ۱۰

حداکثر حجم ممکن استوانه‌ای را به دست آورید که در یک مخروط با ارتفاع $$H$$ و شعاع $$R$$ محاط شده است (شکل ۱0 (الف)).

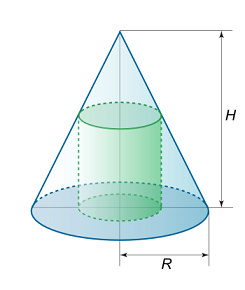
حل: شعاع قاعده استوانه را با $$x$$ و ارتفاع آن را با $$y$$ مشخص می‌کنیم (شکل ۱۰ (ب)).

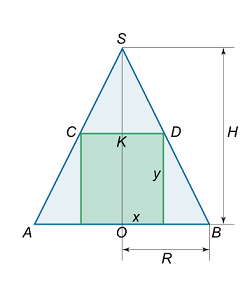
با توجه به تشابه مثلث‌های $$ SKD $$ و $$ SOB $$، داریم:

$$ \large { \frac { { K D } } { { O B } } = \frac { { S K } }{ { S O } } } \; \; \; \kern-0.3pt { \text {or} \; \; \; \frac { x } { R } = \frac { { H – y } } { H } .} $$

معادله اخیر، رابطه بین متغیرهای $$x$$ و $$y$$ را بیان می‌کند. پارامتر $$y$$ را بر حسب $$x$$ می‌نویسیم:

$$ \large \begin {align*}
\frac { x } { R } = \frac { { H – y } } { H } , \; \; & \Rightarrow { H X = \left ( { H – y } \right ) R , \; \; } \Rightarrow { H x = H R – R y , \; \; } \\ & \Rightarrow { y = \frac { { H R – H x } } { R } = H \left ( { 1 – \frac { x } { R } } \right ) . }
\end {align*} $$

حجم محاط شده در استوانه با فرمول زیر بیان می‌شود:

$$ \large V = \pi { x ^ 2 } y . $$

با نوشتن حجم بر حسب متغیر $$x$$، داریم:

$$ \large { V \left ( x \right ) = \pi { x ^ 2} H \left ( { 1 – \frac { x } { R } } \right ) } = { \pi H\left ( { { x ^ 2 } – \frac { { { x ^ 3 } } } { R } } \right ) .} $$

برای به دست آوردن بزرگترین حجم ممکن، از تابع $$V(x)$$ مشتق می‌گیریم:

$$ \large \begin {align*}
V’ \left ( x \right ) = { \left [ { \pi H \left ( { { x ^ 2 } – \frac { { { x ^ 3 } } } { R } } \right ) } \right ] ^ \prime } = { \pi H \left ( { 2 x – \frac { { 3 { x ^ 2 } } } { R } } \right ) ; }
\end {align*} $$

جواب $$ {x_1} = 0 $$، متناظر با صفر بودن حجم استوانه است و از نظر فیزیکی مفهومی ندارد. وقتی از نقطه $$ {x_2} = \large\frac{{2R}}{3}\normalsize $$ عبور کنیم، علامت مشتق از مثبت به منفی تغییر می‌کند. بنابراین، $$ x = \large\frac{{2R}}{3}\normalsize $$ نقطه‌ ماکزیمم تابع $$ V(x)$$ است. به ازای این مقدار، ارتفاع استوانه برابر است با:

$$ \large \require {cancel} { y = H \left ( { 1 – \frac { x } { R } } \right ) } = { H \left ( { 1 – \frac { { 2 \cancel { R } } } { { 3 \cancel { R } } } } \right ) = \frac { H } { 3 } . } $$

در نتیجه، بزرگترین حجم ممکن برای استوانه محاط شده در مخروط، برابر خواهد بود با:

$$ \large { { V _ { \max } } = \pi { x ^ 2 } y } = { \pi { \left ( { \frac { { 2 R } } { 3 } } \right ) ^ 2 } \cdot \frac { H } { 3 } } = { \frac { 4 } { { 2 7 } } \pi { R ^ 2 } H . } $$

این مقدار، برابر با $$ \large\frac{4}{9}\normalsize $$ حجم مخروط است.

مثال ۱۱

مشخصات مخروطی محاط در یک کره به شعاع $$R$$ را بیابید که حجم آن بیشترین مقدار ممکن باشد.

حل: برش مقطعی مخروط محاط در کره در شکل ۱۱ نشان داده شده است.

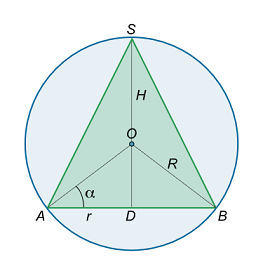
پارامتر $$H$$ را به عنوان ارتفاع مخروط، $$r$$ را به عنوان شعاع قاعده مخروط و $$ \alpha $$ را به عنوان زاویه بین شعاع کره و قاعده مخروط در نظر می‌گیریم. شعاع قاعده و ارتفاع مخروط توسط فرول‌های زیر با شعاع کره مرتبط هستند:

$$ \large { r = R \cos \alpha , } \; \; \; \kern-0.3pt { H = R \sin \alpha + R . } $$

در این حالت، حجم مخروط را می‌توان به صورت زیر نوشت:

$$ \large \begin {align*}
V & = \frac { 1 } { 3 } \pi { r ^ 2 } H = { \frac { 1 } { 3 } \pi { \left ( { R \cos \alpha } \right ) ^ 2 } \left ( { R \sin \alpha + R } \right ) } \\ & = { \frac { 1 } { 3 } \pi { R ^ 3 } { \cos ^ 2 } \alpha \left ( { \sin \alpha + 1} \right).}
\end {align*} $$

که در آن، $$ \alpha $$ در محدوده $$ 0 < \alpha < {\large\frac{\pi }{2}\normalsize} $$ قرار دارد. از حجم $$V$$ نسبت به $$ \alpha $$ مشتق می‌گیریم:

$$ \large \begin {align*}
V’ \left ( \alpha \right ) & = { { \left [ { \frac { 1 } { 3 } \pi { R ^ 3 } { { \cos } ^ 2 } \alpha \left ( { \sin \alpha + 1 } \right ) } \right ] ^ \prime } } \\ &= { \frac { 1 } { 3 } \pi { R ^ 3 }{ \left [ { { { \cos } ^ 2 } \alpha \left ( { \sin \alpha + 1 } \right ) } \right ] ^ \prime } } \\ &= { { \frac { 1 } { 3 } \pi { R ^ 3 } \cos \alpha } \cdot \kern0pt { \left [ { { { \cos } ^ 2 } \alpha – 2 { { \sin } ^ 2 } \alpha – 2 \sin \alpha } \right ] } ; }
\end {align*} $$

مشتق بالا را برابر با صفر قرار می‌دهیم:

$$ \large { V’ \left ( \alpha \right ) = 0 , \; \; } \Rightarrow { { \frac { 1 } { 3 } \pi { R ^ 3 } \cos \alpha } } \cdot \kern0pt { { \left [ { { { \cos } ^ 2 } \alpha – 2 { { \sin } ^ 2 } \alpha – 2 \sin \alpha } \right ] = 0 . } } $$

دو حالت مختلف رخ می‌دهد:

$$ \large { 1 ) \; \cos \alpha = 0 , \; \; } \Rightarrow { \alpha = \frac { \pi } { 2 } ; } $$

$$ \large \begin {align*}
& 2 ) \; { \cos ^ 2 } \alpha – 2 { \sin ^ 2 } \alpha – 2 \sin \alpha = 0 , \; \; \Rightarrow { 1 – 3 { \sin ^ 2 } \alpha – 2 \sin \alpha = 0 , \; \; } \\ & \Rightarrow { 3 { \sin ^ 2 } \alpha + 2 \sin \alpha – 1 = 0 , \; \; } \Rightarrow { \sin \alpha = t , \; \; } \Rightarrow { 3 { t ^ 2 } + 2 t – 1 = 0 , \; \; } \\ & \Rightarrow { D = 4 – 4 \cdot 3 \cdot \left ( { – 1 } \right ) = 1 6 , \; \; } \Rightarrow { { t _ { 1 , 2 } } = \frac { { – 2 \pm \sqrt { 1 6 } } } { 6 } ; \; \; }
\end {align*} $$

$$ \large \begin {align*}
{ t _ 1 } & = – 1 , \; \; \Rightarrow { \sin \alpha = – 1 , \; \; } \Rightarrow { \alpha = \frac { { 3 \pi } } { 2 } } , \\
{ t _ 2 } & = \frac { 1 } { 3 } , \; \; \Rightarrow { \sin \alpha = \frac { 1 } { 3 } . }
\end {align*} $$

همان‌طور که می‌بینیم، پاسخ مورد نظر $$ \sin \alpha = \large\frac{1}{3}\normalsize $$ است. می‌توانیم این پاسخ را با افزایش $$ \alpha $$ و عبور از آن بررسی کنیم. خواهیم دید که علامت مشتق از مثبت به منفی تغییر می‌کند.

کسینوس زاویه $$ \alpha $$‌ برابر است با:

$$ \large { \cos \alpha = \sqrt { 1 – { { \left ( { \frac { 1 } { 3 } } \right ) } ^ 2 } } } = { \sqrt { 1 – \frac { 1 } { 9 } } = \frac { { 2 \sqrt 2 } } { 3 } .} $$

در نتیجه، شعاع قاعده و ارتفاع مخروط متناظر با حجم حداکثر، به صورت زیر خواهند بود:

$$ \large { r = \frac { { 2 \sqrt 2 } } { 3 } R , } \; \; \; \kern -0.3pt { { H = R \cdot \frac { 1 } {3 } + R } = { \frac { 4 }{ 3 } R . } } $$

حجم ماکزیمم نیز برابر است با:‌

$$ \large \begin {align*}
V & = \frac { 1 } { 3 } \pi { r ^ 2 } H = { \frac { \pi } { 3 } \cdot { \left ( { \frac { { 2 \sqrt 2 } } { 3 } } \right ) ^ 2 } \cdot \frac { 4 } { 3 } R } \\ & = { \frac { \pi } { 3 } \cdot \frac { 8 } { 9 } { R ^ 2 } \cdot \frac { 4 } { 3 } R } = { \frac { { 3 2 } } { { 8 1 } } \pi { R ^ 3 } }
\end {align*} $$

که $$ \large\frac{{8}}{{27}}\normalsize $$ حجم کره است.

مثال 12

مخروطی به حجم $$V$$ را در نظر بگیرید. به ازای چه شعاع قاعده ($$R$$) و ارتفاعی ($$H$$) سطح جانبی مخروط کمینه می‌شود؟

حل: ارتفاع خمشی مخروط با $$m$$ مشخص شده است (شکل ۱۲ (الف)).

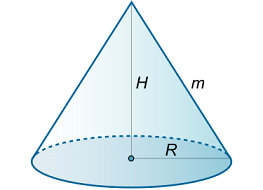
مساحت سطح جانبی با استفاده از فرمول زیر به دست می‌آید:

$$ \large { S _ { \text {L} } } = \pi Rm . $$

در ادامه، برای سادگی، سطح جانبی را با $$S$$ نمایش می‌دهیم. حجم مخروط برابر است با:

$$ \large V = \frac { 1 } { 3 } \pi { R ^ 2 } H $$

ارتفاع $$H$$ را بر حسب $$R$$ و $$V$$ می‌نویسیم:

$$ \large H = \frac { { 3 V } } { { \pi { R ^ 2 } } } . $$

با استفاده از قضیه فیثاغورس، داریم:

$$ \large { m = \sqrt { { H ^ 2 } + { R ^ 2 } } } = { \sqrt { { { \left ( { \frac { { 3 V } } { { \pi { R ^ 2 } } } } \right ) } ^ 2 } + { R ^ 2 } } . } $$

در ادامه، مساحت سطح جانبی را به صورت تابعی از شعاع قاعده $$R$$ می‌نویسیم:‌

$$ \large \begin {align*}
S & = \pi R m = { \pi R \sqrt { { { \left ( { \frac { { 3 V } } { { \pi { R ^ 2 } } } } \right ) } ^ 2 } + { R ^ 2 } } } = { \pi R \sqrt { \frac { { 9 { V ^ 2 } } } { { { \pi ^ 2 } { R ^ 4 } } } + { R ^ 2 } } } \\ & = { \pi R \sqrt { \frac { { 9{ V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } { { { \pi ^ 2 } { R ^ 4 } } } } } = { \frac { { \cancel { \pi } \cancel { R } } } { { \cancel { \pi } { R ^ { \cancel { 2 } } } } } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } \\ & = { \frac { { \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } { R } . }
\end {align*} $$

مشتق این تابع، به صورت زیر است:‌

$$ \large \begin {align*}
S’ \left ( R \right ) & = { { \left ( { \frac { { \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } { R } } \right ) ^ \prime } } = { \frac { { \frac { { 6 { \pi ^ 2 } { R ^ 5 } } } { { 2 \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } \cdot R – \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } { { { R ^ 2 } } } } \\ & = { \frac { { 6 { \pi ^ 2 } { R ^ 6 } – 2 \left ( { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } \right ) } } { { 2 { R ^ 2 } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } } = { \frac { { 4 { \pi ^ 2 }{ R ^ 6 } – 1 8 { V ^ 2 } } } { { 2 { R ^ 2 } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } } \\& = { \frac { { 2 { \pi ^ 2 } { R ^ 6 } – 9 { V ^ 2 } } } { { { R ^ 2 } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } .}
\end {align*} $$

با صفر قرار دادن مشتق بالا، داریم:‌

$$ \large { 2 { \pi ^ 2 } { R ^ 6 } – 9 { V ^ 2 } = 0 , \; \; } \Rightarrow { { R ^ 6 } = \frac { { 9 { V ^ 2 } } } { { 2 { \pi ^ 2 } } } , \; \; } \Rightarrow { R = \sqrt [ \large 6 \normalsize ]{ { \frac { { 9 { V ^ 2 } } } { { 2 { \pi ^ 2 } } } } } . } $$

با افزایش $$R$$ و عبور از نقطه بحرانی، علامت مشتق از منفی به مثبت تغییر می‌کند. در نتیجه، تابع $$S(R)$$ در این نقطه، کمینه است.

ارتفاع مخروط، برابر است با:

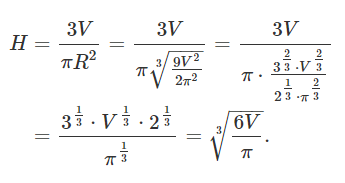
برای درک بهتر شکل بهینه مخروط، نسبت $$ \large\frac{H}{R}\normalsize $$ را محاسبه می‌کنیم:

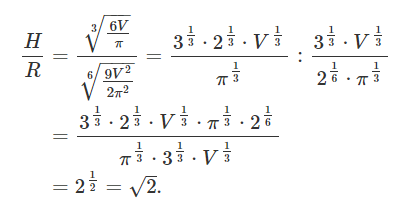
بنابراین، ارتفاع مخروط برای آنکه مساحت سطح جانبی حداقل باشد، حدود $$1.4$$ برابر بزرگتر از شعاع قاعده است.

جالب است بدانید که نسبت ارتفاع به شعاع قاعده سازه غول پیکری به نام «مرکز تفریحی خان‌چادر» (Khan Shatyr Entertainment) مشابه عددی است که در این مثال به دست آوردیم.

مثال ۱3

سطح مقطع جسمی مطابق شکل ۱۳ است. ارتفاع $$H$$ استوانه و شعاع $$R$$ نیم‌کره را به گونه‌ای محاسبه کنید که مساحت آن در حجم ثابت $$V$$ کمینه شود.

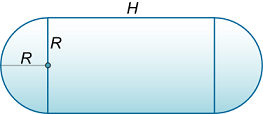
حل: حجم برابر است با:

$$ \large { V = \frac { 4 } { 3 } \pi { R ^ 3 } + \pi { R ^ 2 } H } = { \pi { R ^ 2 } \left ( { \frac { { 4 R } } { 3 } + H } \right ) . } $$

ارتفاع را نیز به صورت زیر بیان می‌کنیم:

$$ \large H = \frac { V } { { \pi { R ^ 3 } } } – \frac { { 4 R } } { 3 } . $$

کل مساحت جسم نیز برابر است با:

$$ \large S = 4 \pi { R ^ 2 } + 2 \pi R H . $$

با جایگذاری عبارت $$H$$ در فرمول قبل، داریم:

$$ \large \begin {align*}
S & = S \left ( R \right ) = { 4 \pi { R ^ 2 } + 2 \pi R \left ( { \frac { V } { { \pi { R ^ 3 } } } – \frac { { 4 R } } {3 } } \right ) } \\ &= { 4 \pi { R ^ 2 } + \frac { { 2 V } } { R } – \frac { { 8 \pi { R ^ 2 } } } { 3 } } = { \frac { { 4 \pi { R ^ 2 } } } { 3 } + \frac { { 2 V } } { R } .}
\end {align*} $$

اکنون مشتق $$S(R)$$ را محاسبه می‌کنیم:

$$ \large \begin {align*}
S’ \left ( R \right ) & = { { \left ( { \frac { { 4 \pi { R ^ 2 } } } { 3 } + \frac { { 2 V } } { R } } \right ) ^ \prime } } = { \frac { { 4 \pi } } { 3 } \cdot 2 R – \frac { { 2 V } } { { { R ^ 2 } } } } \\ &= { \frac { { 8 \pi R } } { 3 } – \frac { { 2 V } } { { { R ^ 2 } } } } = { \frac { { 8 \pi { R ^ 3 } – 6 V } } {{ 3 { R ^ 2 } } } . }
\end {align*} $$

در نتیجه، نقطه اکسترمم به صورت زیر خواهد بود:

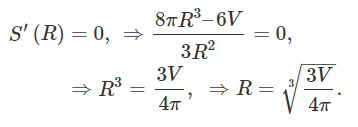
واضح است که در نقطه بالا، تابع کمینه می‌شود. اکنون ارتفاع متناظر با این مقدار را محاسبه می‌کنیم:

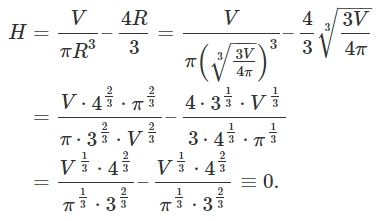
همان‌طور که می‌بینیم، شکل مورد نظر، باید کره‌ای بدون بخش استوانه‌ای باشد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضیات عمومی ۱
• آموزش های رایگان ریاضی و فیزیک
• مشتق زنجیره ای — به زبان ساده
• مشتق مراتب بالاتر — از صفر تا صد
• کاربرد‌ها، روش‌ های محاسبه و مفاهیم مشتق — مجموعه مقالات وبلاگ فرادرس

^^

فیلم‌ های آموزش کاربرد بهینه سازی در هندسه — به زبان ساده (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی کاربرد بهینه‌‌سازی در هندسه

فیلم آموزشی حل چند مثال از کاربرد بهینه‌‌سازی در هندسه