برآوردگر M یا M-Estimator — به زبان ساده

در آمار و روش‌های برآوردیابی، برآوردگر ام (M-Estimator) در گروه برآوردگرهایی قرار می‌گیرد که براساس بیشینه‌سازی یک تابع هدف برحسب میانگین نمونه تصادفی حاصل می‌شوند. برآوردیابی حداکثر درستنمایی (Maximum Likelihood Estimation) و حداقل مربعات عیر خطی حالت خاصی از برآوردگر ام محسوب می‌شوند. برای آنکه خواندن نام این برآوردگر در فارسی راحت‌تر شود از این به بعد آن را برآوردگر M یا M-Estimator و شیوه‌ای که برای بدست آوردن این برآوردگر به کار می‌رود را برآوردیابی M می‌نامیم.

برای آشنایی بیشتر با شیوه برآوردیابی و استفاده از تابع درستنمایی بهتر است نوشتار تابع درست نمایی (Likelihood Function) و کاربردهای آن — به زبان ساده را مطالعه کنید. همچنین خواندن آماره‌ کامل و آماره کمکی — به زبان ساده نیز خالی از لطف نیست.

برآوردگر M یا M-Estimator

انگیزه ایجاد برآوردگر M، آن است که بتوان به یک برآوردگر استوار (Robust) دست یافت که حتی برای داده‌هایی خارج از توزیع نرمال نیز قابل اتکا باشد. معمولا برآوردگر M براساس صفر شدن یک تابع برحسب برآوردگر حاصل می‌شود. تابع برآوردگر (Estimating Function) اغلب مشتق یک تابع آماری دیگر است.

فیلم آموزش روش تحقیق – نحوه نگارش پایان نامه در فرادرس

کلیک کنید

برای مثال برآورد حداکثر درستنمایی (Maximum Likelihood Estimate)، نقطه‌ای را پیدا می‌کند که در آن مشتق تابع درستنمایی نسبت به پارامتر، صفر باشد. واضح است که در این حالت برآوردگر درستنمایی یک نقطه بحرانی برای «تابع امتیاز» (Score Function) است. به این ترتیب می‌توان برآوردگرهای M را به عنوان مشخصه جامعه آماری در نظر گرفت.

نکته: معمولا به مشتق لگاریتم تابع درستنمایی نسبت به پارامتر مجهول، تابع امتیاز یا Score Function می‌گویند.

 $$\large {\displaystyle s(\theta )\equiv {\frac {\partial \log {\mathcal {L}}(\theta )}{\partial \theta }}}$$

تعریف برآوردگر M

می‌توان برآوردگر M را الگویی برای روش حداقل مربعات (Least Square) در نظر گرفت، زیرا مبنای پیدا کردن برآوردگر در این روش، کمینه‌سازی یک تابع هدف است. همچنین روش حداکثر درستنمایی (ML) نیز در گروه برآوردگر M یا M-Estimator قرار می‌گیرد. بنابراین اگر $$f(x;\theta)$$ را تابع چگالی یک توزیع و $$\theta$$ را پارامتر توزیع در نظر بگیریم، برآوردگر حداکثر درستنمایی، نقطه‌ای است که در رابطه زیر صدق کند. چنین برآوردگری را معمولا به صورت MLE یا Maximum Likelihood Estimator نشان می‌دهند.

$$\large \widehat {\theta }=\arg \max _{{\displaystyle \theta }}{\left(\prod _{{i=1}}^{n}f(x_{i},\theta )\right)}\,\!$$

یا به صورت مشابه می‌توان رابطه زیر را برای این برآوردگر در نظر گرفت.

$$\large {\displaystyle {\widehat {\theta }}=\arg \min _{\displaystyle \theta }{\left(\sum _{i=1}^{n}-\log {(f(x_{i},\theta ))}\right)}\,\!}$$

نکته: از خصوصیات جالب برای برآوردگرهای درستنمایی می‌توان به سازگاری آن‌ها اشاره کرد. به این معنی که با افزایش تعداد نمونه، برآوردگر حاصل از روش حداکثر درستنمایی به پارامتر جامعه میل خواهد کرد. ولی این امر ممکن است برای اندازه نمونه‌های کوچک صادق نباشد.

هوبر (Peter Huber) در سال ۱۹۶۴، برآوردگرهای حداکثر درستنمایی تعمیم یافته (Generalize Maximum Likelihood Estimator) را به شکلی معرفی کرد که تابع زیر را کمینه سازند.

$$\large \sum _{{i=1}}^{n}\rho (x_{i},\theta ),\,\!$$

رابطه ۱

بطوری که رابطه زیر برقرار باشد.

$$\large {\hat {\theta }}=\arg \min _{{\displaystyle \theta }}\left(\sum _{{i=1}}^{n}\rho (x_{i},\theta )\right)\,\!$$

رابطه ۲

در این بین تابع $$\rho$$ دارای خصوصیاتی است که در ادامه فهرست شده‌ است.

• این تابع نامنفی است و مقدار کمینه آن صفر خواهد بود.

$$\large \rho(r)\geq 0 ,\;\;\forall r$$

• تابع $$\rho$$ یک تابع زوج است.

$$\large \rho(r)=\rho(-r)$$

• این تابع نسبت به پارامترش یعنی $$r$$ یک تابع صعودی است. ولی شدت رشد آن به میزان رشد $$r$$ نیست.

$$\large \frac{\partial \rho(r)}{\partial r}\geq 0$$

انواع برآوردگر M

همانطور که در قسمت قبل بیان شد، برآوردگر M از طریق کمینه سازی تابع $$\rho(x,\theta)$$ حاصل می‌شود.

فیلم آموزش آمار ریاضی ۲ – آزمون فرض در فرادرس

کلیک کنید

اگر این تابع را براساس یک نمونه تصادفی $$n$$تایی، ایجاد کنیم، خواهیم داشت:

$$\large\sum _{{i=1}}^{n}\rho (x_{i},\theta )\,\!$$

کمینه‌سازی این تابع ممکن است به روش مستقیم صورت گیرد. البته شاید ساده‌تر باشد که بوسیله مشتق‌گیری نسبت به $$\theta$$ و حل معادله و بدست آوردن ریشه‌های معادله برحسب مشتق، به مقدار کمینه و در نتیجه برآوردگر M برسیم. ولی شاید مشتق تابع $$\rho$$ به سادگی صورت نگیرد و یا امکان حل معادله وجود نداشته باشد.

در زمانی که به روش مشتق‌گیری به پاسخی برای ریشه‌های مشتق تابع $$\rho$$ می‌رسیم، برآوردگر M را «نوع $$\Psi$$» یا ($$\Psi$$ Type) می‌نامند. در غیر اینصورت اگر کمینه‌سازی به روش‌های دیگر صورت گیرد، برآوردگر M را «نوع $$\rho$$» یا ($$\rho$$ Type) می‌گویند.

در اغلب موارد برآوردگر M‌ از نوع $$\Psi$$ است.

برآوردگر M از نوع $$\Psi$$

زمانی که تابع $$\rho$$ مشتق‌پذیر باشد، بدست آوردن برآوردگر M برای پارامتر $$\theta$$ ساده خواهد بود. هر چند ممکن است مشتق‌گیری مراحل طولانی و زمان‌بری داشته باشد ولی به هر حال با بدست آوردن مشتق و برابر قرار دادن آن با صفر، به یک معادله خواهیم رسید که برآوردگر M‌ ریشه‌های این معادله خواهند بود.

فرض کنید که $$T$$ یک برآوردگر M برای پارامتر $$\theta \in \Theta$$ باشد. به این ترتیب می‌توان تابع $$\Psi$$ را به صورت زیر در نظر گرفت:

$$\large \Psi :{\mathcal {X}}\times \Theta \rightarrow {\mathbb {R}}^{r}$$

در این جا $$T$$ یک تصویر از تابع توزیع احتمال $$F$$ به فضای پارامتر ایجاد می‌کند.

$$\large T(F) \in \Theta$$

به این ترتیب دستگاه معادلاتی که باید حل شوند به شکل زیر خواهند بود.

$$\large \int _{{{\mathcal {X}}}}\psi (x,\theta )\,dF(x)=0\\ \large {\displaystyle \int _{\mathcal {X}}\psi (x,T(F))\,dF(x)=0}$$

برای مثال، برآوردگر حداکثر درستنمایی به شکل زیر نوشته خواهد شد به شرطی که تابع چگالی موجود بوده یعنی $$f(x,\theta )={\frac {\partial F(x,\theta )}{\partial x}}$$.

$$\large\psi (x,\theta )=\left({\frac {\partial \log(f(x,\theta ))}{\partial \theta ^{1}}},\dots ,{\frac {\partial \log(f(x,\theta ))}{\partial \theta ^{p}}}\right)$$

به این ترتیب اگر تابع $$\rho$$‌ پیوسته و دارای مشتق مرتبه اول برحسب $$\theta$$ باشد، آنگاه شرط لازم برای آنکه برآوردگر M‌ از نوع $$\Psi$$ باشد آن است که:

$$\large {\displaystyle \psi (x,\theta )=\nabla _{\theta }\rho (x,\theta )}$$

برآوردگر نوع $$\rho$$

فرض کنید که $$ {\displaystyle ({\mathcal {X}},\Sigma )}$$ و $$ (\Theta \subset {\mathbb {R}}^{r},S) $$ فضای اندازه‌پذیر براساس مقادیر صحیح $$r$$ باشند. از طرفی $$\theta\in \Theta$$ نیز برداری از پارامترها است که علاقمند به برآورد کردن آن‌ها هستیم. برآوردگر M از نوع $$\rho$$ را که با $$T$$‌ نشان می‌دهیم، بوسیله تابع $$\rho$$ به صورت زیر تعریف می‌شود.

$$\large {\displaystyle \rho :{\mathcal {X}}\times \Theta \rightarrow \mathbb {R} } $$

آنگاه $$T(F) \in \Theta$$ مقدار انتگرال زیر را کمینه می‌سازد.

$$\large {\displaystyle \int _{\mathcal {X}}\rho (x,\theta )dF(x)}$$

به این ترتیب خواهیم داشت:

$$\large T(F)=\arg \min _{{\theta \in \Theta }}\int _{{{\mathcal {X}}}}\rho (x,\theta )dF(x)$$

برای مثال برآوردگر حداکثر درستنمایی، همان برآوردگر M‌ است اگر:

$$\large {\displaystyle \rho (x,\theta )=-\log(f(x,\theta ))}$$

و

$$\large f(x,\theta )={\frac {\partial F(x,\theta )}{\partial x}}$$

نیز تابع چگالی احتمال باشد.

خصوصیات برآوردگر M

فرض کنید که با $$n$$ مشاهده از متغیر تصادفی $$X$$ مواجه هستید. از آنجایی که این مشاهدات از یکدیگر مستقل و هم توزیع با $$F_\theta(x)$$ هستند، برآوردگر حداکثر درستنمایی $$T_n=T_n(x_1,x_2,\ldots,x_n)$$ که تابع زیر را بیشینه سازد، برآوردگر درستنمایی یا همان برآوردگر M خواهد بود.

$$\large \prod_{i=1}^nf_{T_n}(x_i)$$

واضح است که برای حداکثر سازی این تابع می‌توان از مشتق استفاده کرد. با توجه به اینکه $$f_{\theta}(x)$$‌ به ازاء همه مقادیر $$x$$ و $$\theta$$‌ مثبت است، می‌توانیم تابع $$\rho$$‌ را به صورت زیر در نظر بگیریم.

$$\large \rho(x,\theta) = \sum_{i=1}^n[-\ln(f_{T_n}(x_i)]$$

به این ترتیب در یک نمونه متناهی، برآوردگر M‌ تعریف می‌شود. ولی در حالت کلی می‌توان با توجه به رابطه ۱ و ۲، برآوردگر M را تعریف کرد. متاسفانه پیدا کردن تابع $$\rho$$ همیشه به سادگی صورت نمی‌گیرد. به همین دلیل کمتر از برآوردگر M استفاده می‌شود.

می‌توان نشان داد که برآوردگر M بطور مجانبی دارای توزیع نرمال است. به این ترتیب می‌توان فواصل اطمینان و آزمون فرض را با استفاده از «رویکرد والد» (Wald Approach) تشکیل داد. همچنین «تابع اثر» (Influence Function) برای یک برآوردگر M از نوع $$\Psi$$ متناسب با تابع $$\Psi$$‌ است. در نظر بگیرید که $$G$$ یک تابع توزیع احتمال و $$T$$ نیز یک برآوردگر M برای پارامتر $$T(G)$$ باشد. تابع اثر که با $$IF$$ نشان داده می‌شود به صورت زیر خواهد بود.

$$\large \operatorname {IF}(x;T,G)=-{\frac {\psi (x,T(G))}{\int \left[{\frac {\partial \psi (y,\theta )}{\partial \theta }}\right]f(y){\mathrm {d}}y}}$$

در رابطه بالا به خوبی دیده می‌شود که تابع اثر با تابع $$\Psi$$ در یک تناسب است و مخرج این نسبت نیز امید ریاضی مشتق تابع $$\Psi$$ برحسب $$\theta$$ است. البته فرض بر این است که تابع چگالی توزیع $$g$$ وجود دارد و با $$f(y)$$ نشان داده است.

از برآوردگر M در برآورد کردن پارامترهای مکان و مقیاس می‌توان استفاده کرد. همچنین در «رگرسیون استوار» (Robust Regression) نیز از برآوردگر M برای پارامترهای مدل استفاده می‌شود.

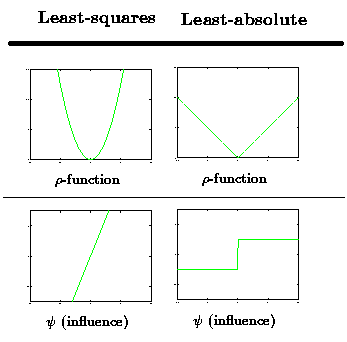
برآوردگر M برای میانگین و میانه

فرض کنید ($$X_1,\ldots,X_n$$) یک نمونه تصادفی مستقل و هم‌توزیع (Independent Identical Distribution) یا iid با توزیع $$F$$ باشند. $$\rho$$ را به صورت زیر در نظر بگیرید:

$$\large \rho (x,\theta )={\frac {(x-\theta )^{2}}{2}},\,\!$$

واضح است که زمانی این تابع به حداقل مقدار خود می‌رسد که $$\theta$$ با میانگین $$X$$‌ها برابر باشد. در نتیجه میانگین نمونه تصادفی یک برآوردگر M برای $$\theta$$ خواهد بود.

واضح است که در این بین $$\rho(x,\theta)$$ یک تابع مشتق‌پذیر و پیوسته برحسب $$\theta$$‌ است. به این ترتیب می‌توان میانگین را یک برآوردگر M از نوع $$\Psi$$ با $$\Psi(x,\theta)$$  به صورت زیر در نظر گرفت.

$$\large {\displaystyle \psi (x,\theta )=\nabla _{\theta }\rho (x,\theta )=\dfrac{\partial\frac{(x-\theta)^2}{2}}{\partial \theta}}=\theta-x$$

برآوردگر M برای میانه

باز هم یک نمونه تصادفی از توزیع $$F$$ را به شکل $$X_1,\ldots,X_n$$، مستقل و هم‌توزیع در نظر بگیرید. به منظور برآورد میانه (Median) این توزیع، تابع $$\rho$$ را برای محاسبات بعدی به صورت زیر در نظر می‌گیریم.

$$\large {\displaystyle \rho (x,\theta )=|x-\theta |}$$

به این ترتیب مقدار کمینه برای این تابع در نقطه‌ای حاصل می‌شود که $$\theta$$ میانه $$X$$‌ها باشد. از آنجایی که تابع $$\rho$$ در این حالت مشتق‌پذیر نیست، می‌توانیم تابع $$\Psi$$ را برحسب زیرمشتق تابع در نظر گرفته و به این ترتیب خواهیم داشت:

$$\large {\displaystyle \psi (x,\theta )=\operatorname {sgn}(x-\theta )}$$

در نتیجه

$$\large {\displaystyle \psi (x,\theta )={\begin{cases}\{-1\},&{\mbox{if }}x-\theta <0\\\{1\},&{\mbox{if }}x-\theta >0\\\left[-1,1\right],&{\mbox{if }}x-\theta =0\end{cases}}}$$

برآوردگر M برای مدل رگرسیونی

فرض کنید که در یک مدل رگرسیونی خطی عادی (ordinary Least Square Regression Model) بخواهیم پارامترها را برآورد کنیم.

فیلم آموزش درس رگرسیون ۱ – رگرسیون خطی در فرادرس

کلیک کنید

در این حالت تابع $$\rho$$ را می‌توان به صورت زیر در نظر گرفت.

$$\large \sum_{i=1}^n\rho(y_i,\beta)=\sum_{i=1}^n(y_i-\sum_{j=1}^k\beta_jx_{ij})^2$$

بوسیله مشتق‌گیری از این تابع به تابع $$\Psi$$ خواهیم رسید. پس کافی است که معادله زیر را برای پیدا کردن برآوردگر M پارامترهای $$\beta$$ به کار ببریم.

$$\large \sum_{i=1}^n\Psi(y_i,\beta)=\sum_{i=1}^n\dfrac{\partial \rho(y_i,\beta)}{\partial \beta}=\sum_{i=1}^n\Psi(y_i-\sum_{j=1}^k\beta_jx_{ij})x_{ij}=0$$

حال اگر به جای استفاده از رگرسیون خطی عادی (OLS) یا (Ordinary Least Square Error) که معمولا از توابع خطای مربع زیان (MSE) یا (Mean Square Error) استفاده می‌شود، از تابع حداقل قدر مطلق تفاضل (LAD) یا (Least Absolute Difference) بهره می‌بردیم، به یک برآوردگر M دیگر برای پارامترهای مدل رگرسیونی دست می‌یافتیم.

خلاصه و جمع‌بندی

در این نوشتار به بررسی برآوردگر M یا M-Estimator پرداختیم و انواع آن را مورد بررسی قرار دادیم. همچنین شیوه بدست آوردن آن را براساس یک مثال برای میانگین و میانه جامعه آماری مرور کردیم. با توجه به اینکه ممکن است جامعه آماری، از توزیع نرمال برخوردار نباشد، برآورد پارامترها از طریق برآوردگرهای M دارای استواری (Robust) بیشتری نسبت به به روش‌های عادی برآوردگریابی مانند روش گشتاوری است.

جدول زیر به بررسی چند تابع $$\rho$$ و نوع تابع اثر پرداخته است. ستون اول تابع زیان و ستون دوم نیز تابع $$\rho$$‌ را نشان می‌دهد. همچنین تابع اثر $$\Psi$$ نیز در ستون آخر مشخص شده است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات
• متغیر تصادفی و توزیع پواسن — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

^^