مساحت دایره به زبان ساده + حل تمرین
مساحت دایره، سطح درون منحنی تشکیل دهنده آن است که معمولا از فرمول πr2 به دست میآید. در این مقاله، فرمولها و روشهای محاسبه مساحت دایره را برای حالتهای مختلف آموزش میدهیم. در انتها نیز ضمن حل چندین مثال متنوع و کاربردی، سایتهای محاسبه آنلاین مساحت دایره را معرفی میکنیم.
دایره چیست ؟
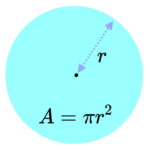
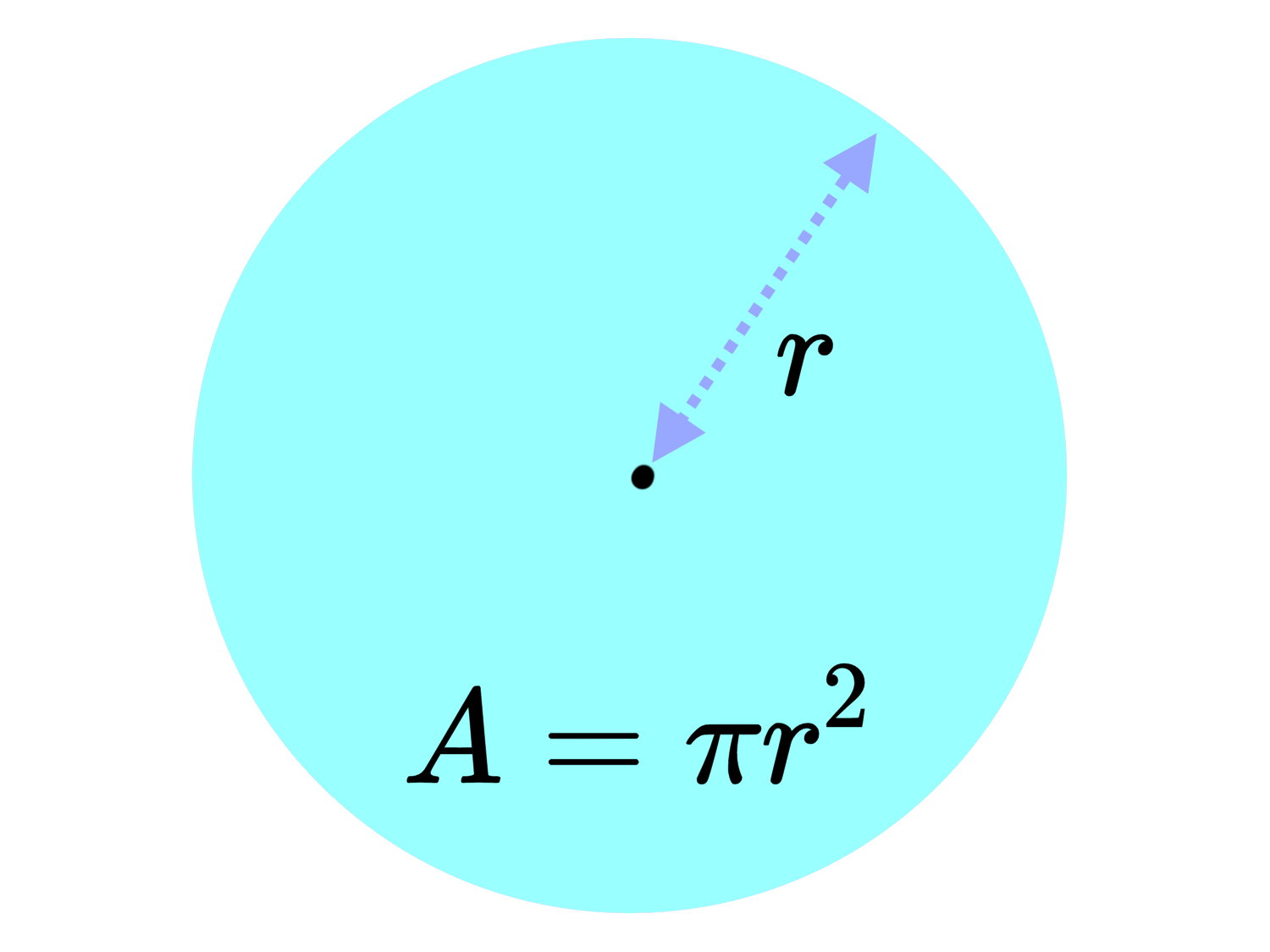
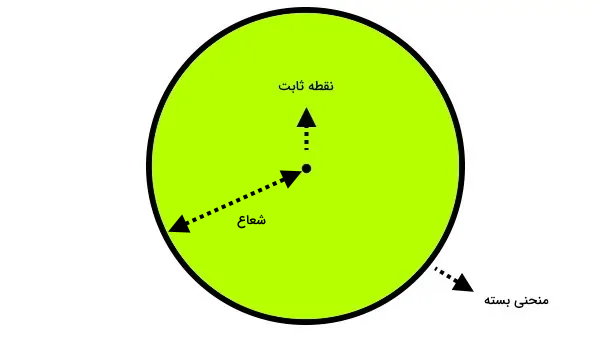
دایره (به انگلیسی Circle)، یکی از اشکال هندسی پایه است که از یک منحنی بسته تشکیل میشود. تمام نقاط تشکیل دهنده دایره، در فاصله برابر از یک نقطه ثابت قرار دارند. به این نقطه ثابت، «مرکز دایره» (Center of Circle) میگویند.
به فاصله نقاط روی منحنی تا مرکز دایره، «شعاع» (Radius) گفته میشود. شعاع، از مهمترین اندازههای دایره است که به منظور محاسبه مساحت و محیط مورد استفاده قرار میگیرد.
اجزای دایره چه هستند؟
دایره از اجزای مختلفی نظیر مرکز، شعاع، قطر، قطاع، قطعه، کمان، مماس، وتر و محیط تشکیل میشود. برخی از این اجزا برای اندازهگیری مساحت کل یا بخشی از دایره مورد استفاده قرار میگیرند.
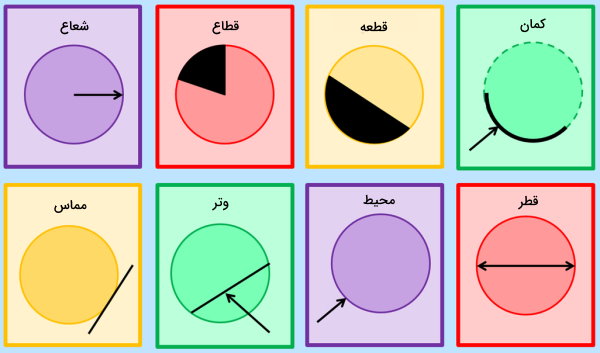
اجزای نمایش داده شده در تصویر بالا، عبارت هستند از:
- شعاع دایره: فاصله ثابت نقاط روی محیط دایره تا مرکز دایره
- کمان: بخشی از منحنی تشکیل دهنده محیط دایره
- قطاع: سطح محدود به یک کمان و دو شعاع دایره (نیمدایره، ثلث دایره، ربع دایره و غیره)
- وتر: پاره خط متصل کننده دو نقطه بر روی محیط دایره (قطر، بزرگترین وتر دایره است.)
- قطر: وتر گذرنده از مرکز دایره (قطر دایره، دو برابر شعاع آن است.)
- قطعه: سطح محدود به کمان و وتر متصل کننده دو انتهای آن
- محیط دایره: منحنی بسته تشکیل دهنده دایره
عدد پی چیست؟
نسبت محیط دایره به قطر آن، همیشه برابر 3/14 است. به این عدد ثابت، عدد پی میگویند. اغلب محاسبات مربوط به محیط و مساحت دایره، با استفاده اندازه اجزای معرفی شده در بخش قبلی و عدد پی انجام میگیرند. از اینرو، به خاطر داشتن مقدار آن، اهمیت بالایی دارد.
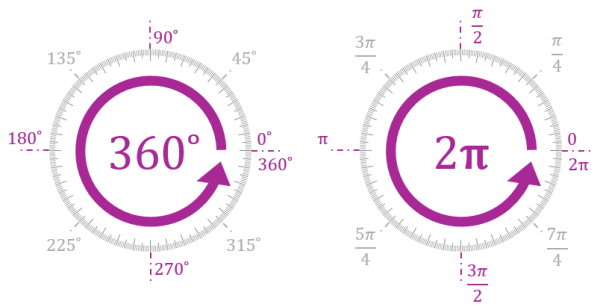
در فرمولهای ریاضی، عدد پی با حرف یونانی π نمایش داده میشود. این عدد، برای تبدیل درجه به رادیان نیز مورد استفاده قرار میگیرد. مجموع زوایای کمانهای دایره برابر 360 درجه یا 2π است. به منظور تبدیل درجه به رادیان و برعکس، میتوانید از تصویر بالا یا فرمول معرفی شده در بخشهای بعدی استفاده کنید.
- مطالب پیشنهادی برای مطالعه:
مساحت دایره چیست ؟
«مساحت دایره» (Area of a Circle)، سطح محدود به محیط دایره است. خط چین قرمز رنگ در تصویر زیر، محدوده یا محیط دایره را نمایش میدهد. بخش هاشور خورده درون این محیط، مساحت دایره است.
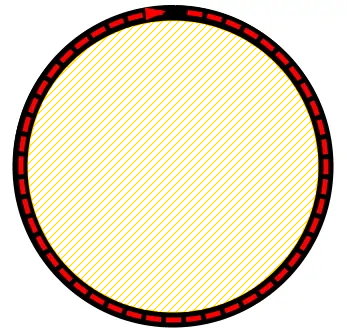
مساحت دایره چگونه بدست می آید ؟
مساحت دایره از ضرب مربع شعاع در عدد ثابت 3/14 به دست میآید (مربع شعاع، اندازه شعاع ضربدر خودش است). فرمول مساحت دایره به صورت زیر نوشته میشود:
- A: مساحت
- π: عدد ثابت 3/14
- r: شعاع دایره
اگر فرمول بالا را بر حسب قطر دایره بازنویسی کنیم، به رابطه زیر میرسیم:
یا
- d: قطر دایره (دو برابر شعاع)
روابط بالا، نمایش مساحت دایره به صورت جبری هستند. البته به غیر از شعاع و قطر، امکان محاسبه مساحت با استفاده از اندازههای دیگر نیز وجود دارد. در ادامه، پس از حل یک مثال با فرمولهای بالا، به معرفی فرمولهای دیگر خواهیم پرداخت.
مثال: مساحت میز دایرهای شکل
شخصی میخواهد برای یک میز دایرهای شکل، رومیزی پارچهای تهیه کند. اگر قطر این میز برابر 1/5 متر باشد، حداقل پارچه مورد نیاز برای پوشاند تمام سطح میز چقدر است؟

برای شروع حل مسئله، ابتدا فرمول مساحت دایره و اندازههای معلوم را یادداشت میکنیم:
- A: مساحت
- π: عدد ثابت 3/14
- r: شعاع دایره برابر 0/75 متر (نصف قطر)
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
مساحت میز دایرهای شکل برابر 1/77 متر مربع است. در نتیجه، برای تهیه رومیزی، به حداقل 1/77 متر مربع پارچه نیاز خواهد بود.
نکته: استفاده از مساحت بر اساس شعاع، مسئله را سادهتر و تعداد محاسبات را کمتر میکند.
فرمول های مساحت دایره
شعاع دایره، یکی از اندازههای مشترک در محاسبه مساحت، محیط، قطاع و بسیاری از اجزای دایره است. از اینرو، امکان نوشتن فرمولهای مساحت دایره بر اساس اندازههای دیگر وجود دارد.
در این بخش، فرمول مساحت دایره بر حسب محیط و فرمول قطاع دایره بر حسب زاویه را به همراه حل مثال معرفی میکنیم.
فرمول مساحت دایره با محیط
محیط دایره، اندازه منحنی تشکیل دهنده آن است. خط چین قرمز در تصویر زیر، مسیر روی نقاط دایره یا محیط دایره را نمایش میدهد.
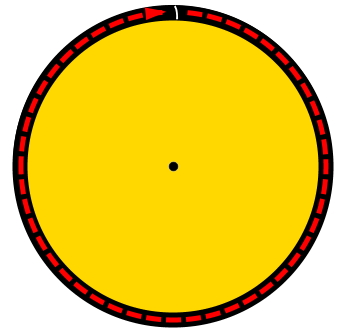
فرمول محیط دایره، به صورت زیر نوشته میشود:
- C: محیط دایره
- π: عدد ثابت 3/14
- r: شعاع دایره
در فرمول محیط دایره، مانند فرمول مساحت دایره، فقط از اندازه شعاع و عدد پی استفاده شده است. در صورت بازنویسی این فرمول بر حسب شعاع، خواهیم داشت:
اگر r در رابطه بالا را درون رابطه مساحت دایره (πr2) قرار دهیم، به فرمول مساحت بر اساس محیط میرسیم:
- A: مساحت دایره
- C: محیط دایره
مثال: محاسبه مساحت دایره از روی محیط
مساحت دایرهای به محیط 60 متر را حساب کنید. (عدد پی را برابر 3 در نظر بگیرید.)
برای حل مثال، فرمول مساحت دایره بر حسب محیط را مینویسیم و و اندازههای معلوم را درون آن قرار میدهیم:
- A: مساحت دایره
- C: محیط دایره برابر 60 متر
- π: عدد ثابت 3 (بر اساس فرض مسئله)
در نتیجه، مساحت دایرهای با محیط 60 برابر با 300 متر مربع خواهد بود.
فرمول مساحت قطاع دایره
قطاع دایره، بخشی از یک دایره فرضی است که از یک کمان و دو شعاع تشکیل میشود. تصویر زیر، یک کیک دایرهای شکل را نمایش میدهد. هر یک از بخشهای این کیک (بخشهای دارای مواد متفاوت)، قطاعهای آن هستند.

فرمول محاسبه مساحت قطاع دایره عبارت است از:
- As: مساحت قطاع دایره
- r: شعاع دایره
- θ: زاویه رو به روی کمان قطاع بر حسب رادیان
اگر زاویه مقابل کمان قطاع، بر حسب درجه بیان شود، باید زاویه را با استفاده از رابطه زیر به واحد رادیان تبدیل کرد:
- rad: زاویه بر حسب رادیان
- deg: زاویه بر حسب درجه
- π: عدد ثابت 3/14
در واقع اگر زاویه مقابل کمان قطاع با واحد درجه را بر 360 (مجموع زوایای مقابل تمام کمانهای دایره) تقسیم کنیم، نسبت مساحت قطاع به مساحت کل دایره به دست میآید. به این ترتیب، با ضرب این نسبت در مساحت کل دایره، مساحت قطاع تعیین میشود.
نیمدایره و ربع دایره، از قطاعهای شناخته شده دایره هستند. این قطاعها، فرمولهای مخصوص به خود برای محاسبه مساحت دارند. در صورت علاقه به آشنایی بیشتر با نحوه محاسبه مساحت نیمدایره و دایره، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- قطاع و مقطع دایره و محاسبات آن در هندسه — به زبان ساده + فیلم آموزش رایگان
- مساحت نیم دایره چگونه بدست میآید؟ — به زبان ساده + حل مثال
- مساحت ربع دایره چیست؟ — به زبان ساده + حل تمرین و مثال
مثال: محاسبه مساحت قطاع پیتزا
قطر پیتزای نمایش داده شده در تصویر زیر، برابر 20 سانتیمتر است. مساحت هر قطاع پیتزا را حساب کنید.(قطاعهای پیتزا را هم اندازه و عدد پی را برابر 3 در نظر بگیرید.)

برای تعیین مساحت هر یک از قطاعهای پیتزا، فرمول مساحت قطاع دایره را مینویسیم:
از بین اندازههای مورد نیاز برای محاسبه مساحت A، شعاع دایره (r=20) را داریم. با این وجود، اندازه زاویه مقابل کمان هر قطاع داده نشده است. بر اساس فرض سوال، هر هشت قطاع با یکدیگر برابر هستند. از آنجایی که مجموع کمانهای هر دایره برابر 360 درجه است، زاویه هر کمان از تقسیم 360 بر تعداد قطاعها به دست میآید:
برای استفاده از زاویه بالا در فرمول، باید واحد آن را به رادیان تبدیل کنیم:
زاویه به دست آمده بر حسب رادیان را به همراه اندازه شعاع در فرمول مساحت قطاع دایره قرار میدهیم:
در نتیجه، مساحت هر قطاع پیتزا حدودا برابر 150 سانتیمتر مربع است. به دلیل برابر بودن تعداد قطاعهای دایره در این مثال، میتوانستیم مساحت هر قطاع را از فرمول اصلی مساحت دایره و تقسیم آن بر عدد 8 به دست بیاوریم.
مثال های مساحت دایره
در این بخش، به حل چندین مثال متنوع در زمینه مساحت دایره، قطاعهای دایره، شکلهای محاطی و شکلهای محیطی میپردازیم.
مثال اول: مقایسه مساحت دایره با شعاعهای متفاوت
دایرههای زیر از راست به چپ دارای شعاعهای 3، 6 و 9 هستند. مساحت هر یک از این دایرهها و رابطه بین مساحتهای آنها را تعیین کنید. (عدد پی را برابر 3 در نظر بگیرید.)

برای شروع محاسبات، ابتدا فرمول مساحت دایره را مینویسیم:
برای محاسبه جداگانه هر یک از مساحتها، علامتهای زیر در نظر میگیریم:
- A1 و r1: مساحت و شعاع دایره شماره 1
- A2 و r2: مساحت دایره شماره 2
- A3 و r3: مساحت دایره شماره 3
به این ترتیب، مساحت دایره شماره 1 برابر است با:
مساحت دایره شماره 2 از فرمول زیر به دست میآید:
مساحت دایره شماره 3 نیز به صورت زیر محاسبه میشود:
برای مقایسه مساحتهای به دست آمده، نسبت آنها را تعیین میکنیم:
همان طور که مشاهده میکنید، با 2 برابر شدن شعاع، مساحت 4 برابر و با 3 برابر شدن شعاع، مساحت 9 برابر میشود. به عبارت دیگر، نسبت مساحت دایرهها، برابر مربع (توان دو) نسبت شعاع آنها است.
مثال دوم: مساحت فضای سبز با محیط
شخصی در حیاط خانه خود، یک فضای سبز دایرهای شکل ساخته است. اگر محیط این فضای سبز برابر 24 متر باشد، مساحت آن چقدر خواهد بود؟ (عدد پی را برابر 3 در نظر بگیرید.)

به منظور تعیین مساحت فضای سبز، فرمول مساحت دایره بر اساس محیط را مینویسیم:
- A: مساحت دایره
- C: محیط دایره برابر 24 متر
- π: عدد ثابت 3
اندازههای معلوم را درون فرمول جایگذاری میکنیم:
مساحت فضای سبز برابر 48 متر مربع است.
مثال سوم: مساحت نیم دایره
شخصی برای ورودی در خانه خود، یک پادری، مشابه تصویر زیر تهیه کرده است. این پادری، چه سطحی از زمین را پوشش میدهد؟

عرض چارچوب در ورودی برابر 90 سانتیمتر است. با توجه به تصویر بالا، این عدد، قطر پادری را نیز نمایش میدهد. پادری، به شکل یک قطاع نیمدایره است. بنابراین، مساحت آن از تقسیم مساحت دایره کامل بر عدد 2 به دست میآید. فرمول مساحت کامل دایره به صورت زیر نوشته میشود:
- A: مساحت دایره کامل
- r: شعاع دایره برابر 45 سانتیمتر (نصف قطر)
- π: عدد ثابت 3/14
اندازههای معلوم را درون فرمول قرار داده و محاسبات را انجام میدهیم:
مساحت پادری، نصف مساحت دایره کامل است:
در نتیجه، پادری، 3179/25 سانتیمتر مربع از سطح مقابل در ورودی را پوشش میدهد. با توجه به مراحل حل این مثال، فرمول محاسبه مساحت نیمدایره به صورت زیر نوشته میشود:
- As: مساحت نیم دایره
مثال چهارم: مساحت ثلث دایره
قطاع دایرهای با شعاع 9 و زاویه مقابل کمان 120 درجه را محاسبه کنید.
اگر زاویه مقابل کمان قطاع برابر 120 درجه باشد، آن قطاع، ثلث یا یک سوم دایره است. مساحت این قطاع، از تقسیم مساحت دایره کامل بر عدد 3 به دست میآید. در نتیجه، مساحت قطاع مورد سوال برابر است با:
- A: مساحت دایره
- r: شعاع قطاع برابر 9
- π: عدد ثابت 3/14
مساحت ثلث دایره برابر 84/78 است.
مثال پنجم: مساحت دایره با زاویه
مساحت قطاع زیر چند است؟
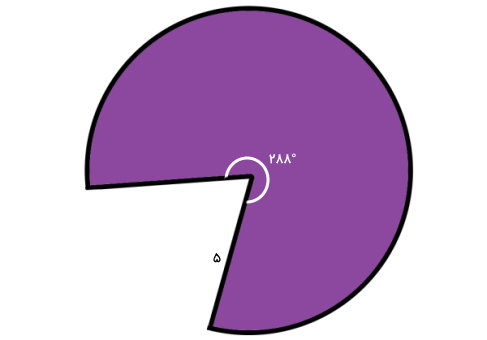
مساحت قطاع دایره توسط فرمول زیر محاسبه میشود:
- As: مساحت قطاع
- r: شعاع قطاع برابر
- θ: زاویه مقابل کمان قطاع
زاویه قطاع را به رادیان تبدیل میکنیم:
مقدار بالا را به همراه شعاع، درون فرمول مساحت قطاع قرار میدهیم:
مساحت قطاع دایره با زاویه 288 درجه و شعاع 5، برابر 62.5 است.
مثال ششم: مساحت بخش هاشور خورده ربع دایره
تصویر زیر، یک ربع دایره با شعاع 8 را نمایش میدهد. مساحت بخش هاشور خورد را حساب کنید. (عدد پی را برابر 3 در نظر بگیرید.)
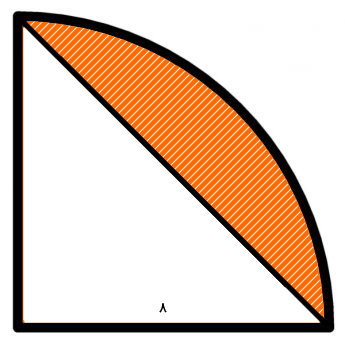
ربع دایره، قطاع یک چهارم یک دایره کامل است. بنابراین، زاویه مقابل کمان قطاع ربع دایره در تصویر بالا برابر با °90=°4÷°360 بود. به این ترتیب، بخش سفید رنگ قطاع، یک مثلث قائم الزاویه را تشکیل میدهد (شعاعهای قطاع، ساقهای مثلث قائم الزاویه هستند). در نتیجه، مساحت بخش هاشور خورده به صورت زیر محاسبه میشود:
مساحت مثلث قائم الزاویه - مساحت ربع دایره = مساحت بخش هاشور خورده
برای حل رابطه بالا، ابتدا مساحت ربع دایره را تعیین میکنیم. این مساحت از تقسیم مساحت دایره کامل بر عدد 4 به دست میآید:
- A: مساحت دایره کامل
- r: شعاع دایره برابر 8
- π: عدد ثابت 3
بنابراین، مساحت ربع دایره برابر است با:
فرمول مساحت مثلث عبارت است از:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
- A: مساحت
- b: یکی از قاعدههای مثلث
- h: ارتفاع نظیر قاعده b
در مثلث قائم الزاویه، ساقها، قاعده و ارتفاع نظیر یکدیگر هستند. بر این اساس، داریم:
با کم کردن این مقدار از مساحت ربع دایره، مساحت قسمت هاشور خورده به دست میآید:
32 -48 = مساحت بخش هاشور خورده
16 = مساحت بخش هاشور خورده
در نتیجه، مساحت بخش هاشور خورده برابر 16 است.
مثال هفتم: مساحت دایره محاطی
اگر محیط مربع نمایش داده شده در تصویر زیر برابر 40 باشد، مساحت دایره محاط در آن چقدر است؟ پس از محاسبه مساحت دایره، مساحت مربع را به دست بیاورید.

قطر دایره محاط در یک مربع، با طول ضلعهای آن مربع برابری میکند. به این ترتیب، با تعیین اندازه ضلعهای مربع، امکان محاسبه مساحت دایره محاطی فراهم میشود. فرمول محیط مربع عبارت است از:
- P: محیط مربع برابر 40
- a: اندازه ضلعهای مربع
$$<br /> \10= a<br /> $$
اندازه ضلع مربع محیطی یا قطر دایره محاطی برابر 10 است. مساحت دایره از رابطه زیر به دست میآید:
- A: مساحت دایره
- r: شعاع دایره برابر 5 (نصف قطر دایره)
- π: عدد ثابت 3.14
مساحت دایره محاط در مربعی با محیط 40، برابر 78/5 است. مساحت مربع، با استفاده از فرمول زیر محاسبه میشود:
- As: مساحت مربع
- a: اندازه ضلع مربع برابر 10
در نتیجه، مساحت مربع محیط بر دایرهای با شعاع 5 برابر 100 است.
مثال هشتم: مساحت دایره محیطی
مساحت دایره محیط بر مربعی به ضلع 10 را حساب کنید.

اگر دایرهای بر یک مربع محیط باشد، اندازه قطر مربع، برابر با اندازه قطر دایره خواهد بود. به این ترتیب، برای محاسبه مساحت دایره بالا، ابتدا باید قطر مربع را تعیین کنیم. قطر مربع برابر است با:
- d: قطر مربع
- a: اندازه ضلع مربع برابر 10
قطر مربع محاط در دایره یا قطر دایره محیط بر مربع برابر است. مساحت دایره به صورت زیر محاسبه میشود:
- A: مساحت دایره
- r: شعاع دایره برابر (نصف قطر دایره)
- π: عدد ثابت 3.14
مساحت دایره محیط بر مربعی با ضلع 10 برابر 314 است.
مثال نهم: پیدا کردن قطر دایره از روی مساحت
قطر دایرهای به مساحت 675 را به دست بیاورید؟ (عدد پی را برابر 3 در نظر بگیرید.)
برای محاسبه قطر دایره، کافی است فرمول مساحت آن را بنویسیم:
- A: مساحت دایره برابر 675
- r: شعاع دایره
- π: عدد ثابت 3
اکنون، اندازههای معلوم را درون فرمول قرار میدهیم و آن را برای تعیین شعاع حل میکنیم:
شعاع این دایره برابر 15 است. در نتیجه، قطر آن برابر با 30 خواهد بود.
محاسبه آنلاین مساحت دایره
یکی از روشهای محاسبه سریع و دقیق مساحت دایره، استفاده از سایتهای اینترنتی است. از کاربردیترین ابزارهای اینترنتی موجود برای این کار میتوان موتور جستجوی Google (+)، سایت Omni Calculator (+) و سایت Calculator.net (+) و Calculatorsoup (+) اشاره کرد.
تصویر زیر، ابزار موتور جستجوی گوگل برای محاسبه آنلاین مساحت دایره را نمایش میدهد.
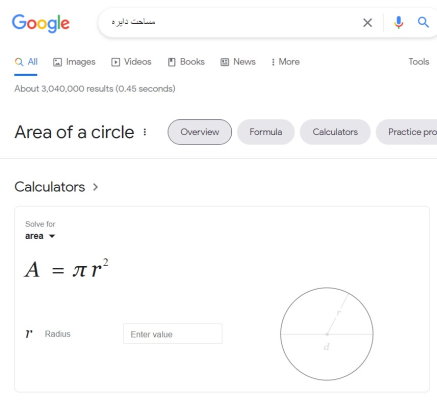
به منظور دسترسی به ابزار گوگل برای محاسبه آنلاین مساحت دایره، عبارتهایی نظیر «مساحت دایره» یا «circle area» را در کادر جستجو تایپ کرده و کلید Enter را فشار دهید. به این ترتیب، ابزاری مشابه تصویر بالا در ابتدای صفحه نتایج گوگل به نمایش در میآید. در صورت تایپ اندازه شعاع در کادر مقابل عنوان «r Radius»، مساحت دایره محاسبه شده و نتیجه محاسبات به همراه روند حل نشان داده میشود.
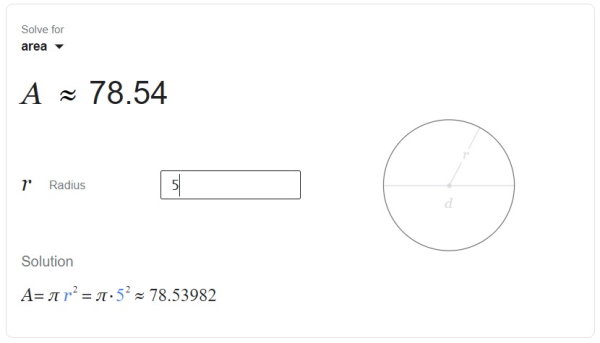
سایتهای معرفیشده در این بخش، برای محاسبه آنلاین محیط دایره و دیگر اندازههای آن نیز کاربرد دارند.
سوالات متداول مساحت دایره
در این بخش، به برخی از سوالات پرتکرار در زمینه مساحت دایره و نحوه محاسبه آن پاسخ میدهیم.
فرمول مساحت دایره با شعاع چیست ؟
فرمول مساحت دایره با شعاع برابر πr2 است. r، شعاع دایره و π، عدد ثابت 3/14 را نمایش میدهد.
فرمول مساحت دایره با قطر چیست ؟
فرمول مساحت دایره با قطر برابر π(d/2)2 است. d، قطر دایره و π، عدد ثابت 3/14 را نمایش میدهد.
فرمول مساحت دایره با محیط چیست ؟
فرمول مساحت دایره با محیط برابر C2/4π است. C، محیط دایره با فرمول 2πr و π، عدد ثابت 3/14 را نمایش میدهد.
مساحت نیم دایره چگونه بدست می آید ؟
مساحت نیم دایره برابر نصف مساحت دایره کامل است. این مساحت از تقسیم فرمول πr2 بر عدد 2 بدست میآید.
مساحت قطاع دایره چگونه بدست می آید ؟
مساحت قطاع دایره از ضرب مربع شعاع (r2) در نصف زاویه قطاع بر حسب رادیان (θ/2) محاسبه میشود.
زاویه دایره چند درجه است ؟
زاویه دایره معادل 360 درجه یا 2π است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه – به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













سلام به بخشید اگر شعاع 5باشه شعاعxشعاع یعنی5 میشی جواب بدن
میشه اسم برنامه ای که ویدیو رو ظبط کردید رو بگید
بی نهایت سپاسگزارم
عالی بود.???
میشه اسم برنامه ای که باهاش این فیلم رو ساختین رو بگید؟ممنون میشم♡