نمایش تاخیر سیستم– از صفر تا صد
یک سیستم میتواند به صورت ذاتی دارای «تاخیر» (Delay) باشد. تاخیر در یک سیستم کنترلی یا تاخیر سیستم را میتوان به صورت واحدی در نظر گرفت که باعث به وجود آمدن یک شیفت زمانی در ورودی سیستم میشود. اما تاخیر سیستم بر مشخصههای سیگنال ورودی تاثیر نمیگذارد. در این مطلب قصد داریم چگونگی نمایش تاخیر سیستم در حوزه لاپلاس را بررسی کنیم و بعد از نمایش تاخیر سیستم با تبدیل لاپلاس، به سادگی میتوان با استفاده از تغییر متغیر، نمایش در سایر حوزهها را نیز به دست آورد.
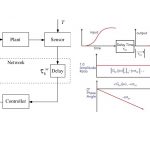
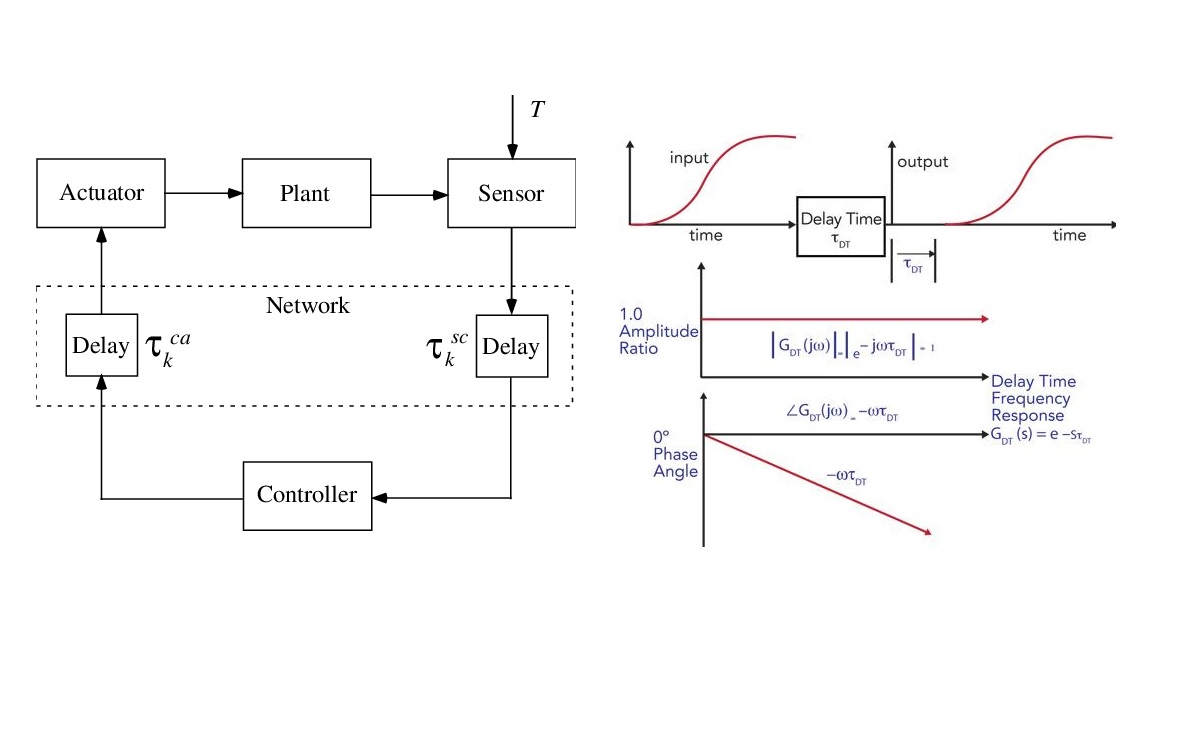
تاخیر سیستم ایدهآل
میتوان گفت یک تاخیر سیستم ایدهآل، تاخیری است که به هیچ وجه ویژگیهای سیگنال را تغییر ندهد و فقط سیگنال را به اندازه یک زمان معین به تعویق بیندازد. بعضی از تاخیرها، مانند «تاخیر پردازش» (Processing Delay) و «تاخیر انتقال» (Transmission Delay) غیرعمدی و غیر قابل اجتناب هستند. سایر انواع تاخیر سیستم مانند «تاخیر سنکرون» (Synchronization Delay) یک بخش جامع از سیستم به حساب میآیند.
تاخیر سیستم ایدهآل باعث میشود که تابع ورودی، در زمان به یک اندازه مشخص رو به جلو شیفت یابد. سیستمهایی که دارای تاخیر ایدهآل هستند، باعث میشوند که خروجی آنها به یک اندازه محدود و از پیش مشخص زمانی به تعویق بیفتد.
شیفت زمانی
فرض کنید که یک تابع در حوزه زمان در اختیار ما قرار دارد که به اندازه یک مقدار زمانی ثابت و مشخص T در زمان شیفت یافته است. برای راحتی میتوان این تابع را با نماد نمایش داد. حال میتوانیم نشان دهیم که تبدیل لاپلاس تابع به صورت زیر به دست خواهد آمد:
از رابطه بالا میتوان نتیجه گرفت که شیفت زمانی یا تاخیر در حوزه زمان، به مقداری نمایی در حوزه مختلط لاپلاس تبدیل خواهد شد.
شیفت در حوزه Z
یک تبدیل ستاره را در نظر میگیریم که بین تبدیل Z و تبدیل ستاره رابطه عمومی زیر وجود داشته باشد:
میتوان نشان داد که یک شیفت زمانی برای مقادیر زمان گسسته، در حوزه Z به صورت زیر نشان داده خواهد شد:
در تصویر زیر رابطه بین تاخیر به اندازه یک واحد و نمایش آن در حوزه تبدیل Z نشان داده شده است.
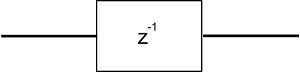
رابطه بین تاخیر و پایداری در یک سیستم
یک شیفت زمانی در حوزه زمان تبدیل به یک رشد نمایی در حوزه لاپلاس میشود. به نظر میرسد که این امر نشان دهنده این واقعیت باشد که شیفت زمانی میتواند روی پایداری سیستم تاثیر بگذارد و حتی در برخی موارد منجر به ناپایداری سیستم شود. به همین دلیل در سیستمهای کنترلی پارامتر جدید به نام «حاشیه زمان» (Time Margin) تعریف میکنند. پارامتر حاشیه زمان برابر با مقدار زمانی است که میتوانیم یک تابع ورودی را به اندازه آن شیفت دهیم، قبل از آن که سیستم ناپایدار شود. اگر یک سیستم بتواند هر مقدار شیفت زمانی را تحمل کند و ناپایدار نشود، در این صورت میگوییم که حاشیه زمان آن سیستم بینهایت است.
حاشیه تاخیر
زمانی که در مورد سیگنالهای سینوسی بحث میکنیم، شاید استفاده از واژه شیفت زمانی مفهوم واضحی نداشته باشد. به همین دلیل در مورد سیگنالهای سینوسی، از مفهومی به نام «شیفت فاز» (Phase Shift) استفاده میکنیم. همچنین بسیار متداول است که برای سیگنالهای سینوسی از «حاشیه فاز» (Phase Margin) به جای حاشیه زمان بهره میگیریم.
در این حالت، میتوان گفت که پارامتر حاشیه فاز، نشان دهنده مقدار شیفت فازی است که میتوانیم به سیگنال ورودی یک سیستم کنترلی وارد کنیم، قبل از آن که سیستم ناپایدار شود. حاشیه فاز برای یک سیستم را با نماد نشان میدهیم و حاشیه فاز مربوط به یک سیستم مرتبه دوم را به صورت زیر تعریف میکنیم:
گاهی میتوان رابطه حاشیه فاز را با رابطه ساده زیر تقریب زد:
حرف یونانی نشان دهنده کمیتی است که «نرخ میرایی» (Damping Ratio) سیستم نام دارد. در مطالب قبلی مجله فرادرس به بررسی کمیتهای مختلف مربوط به پاسخ یک سیستم کنترلی درجه دو پرداختیم.
تاخیر در حوزه تبدیلات مختلف
نمیتوان از تبدیل Z معمولی برای سیستمهایی استفاده کرد که دارای تاخیر زمانی تصادفی و یا تاخیر پردازش هستند. با این حال، میتوان برای چنین سیستمهایی از یک نسخه «تبدیل Z اصلاح شده» (Modified Z-Transform) استفاده کرد. در برخی مراجع به این تبدیل Z اصلاح شده، «تبدیل Z پیشرفته» (Advanced Z-Transform) میگویند.
تبدیل ستاره تاخیر یافته
برای نشان دادن مفهوم تاخیر ایدهآل، میتوانیم بررسی کنیم که تبدیل ستاره چگونه به ورودی تاخیر یافته در زمان با یک مقدار شیفت زمانی برابر با T پاسخ میدهد. تابع تبدیل ستاره تاخیر یافته با پارامتر تاخیر است. تبدیل ستاره تاخیر یافته به صورت زیر تعریف میشود:
همان طور که در رابطه فوق میتوان دید، در تبدیل ستاره، یک سیگنال تاخیر زمانی در یک مقدار نمایی کاهشی در حوزه تبدیل ضرب شده است.
تبدیل Z تاخیر یافته
میدانیم تبدیل ستاره با استفاده از تغییر متغیر زیر با تبدیل Z ارتباط دارد:
در نتیجه میتوانیم این رابطه را تفسیر کنیم و به نحوه پاسخ دادن تبدیل Z متناسب با تاخیر در حوزه زمان، پی ببریم:
مشاهده میکنید که این همان نتیجهای است که انتظار آن را داشتیم. حال که میدانیم چگونه تبدیل Z به تاخیرهای حوزه زمان پاسخ میدهد، میتوانیم این رفتار را به فرمی تعمیم دهیم که به آن تبدیل Z تاخیر یافته میگویند.
تبدیل Z تاخیر یافته یک تابع از دو متغیر و است و به صورت زیر تعریف میشود:
و در نتیجه رابطه زیر به دست می آید:
تبدیل Z اصلاح شده
تبدیل Z تاخیر یافته در برخی مواقع مورد استفاده قرار میگیرد، اما مهندسان و ریاضیدانان تصمیم گرفتند که یک نسخه کاربردیتر از تبدیل Z را به وجود آورند. نسخه جدید تبدیل Z، بسیار شبیه به تبدیل Z تاخیر یافته است و فقط از یک تغییر متغیر در آن استفاده شده است و به آن تبدیل Z اصلاح یافته میگویند. تبدیل Z اصلاح شده بر اساس تبدیل Z تاخیر یافته به صورت زیر تعریف میشود:
این رابطه را به صورت صریح نیز میتوان بر اساس رابطه زیر به دست آورد:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی کنترل
- آموزش سیستم های کنترل خطی
- مجموعه آموزشهای مهندسی برق
- آموزش کنترل مدرن به همراه پیاده سازی در متلب
- معیار پایداری راث هرویتز — به زبان ساده
- کنترل پذیری و رویت پذیری — از صفر تا صد
- جایابی قطب — از صفر تا صد
^^












