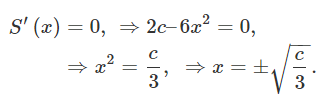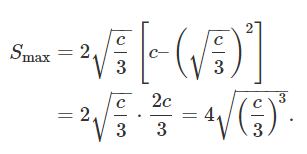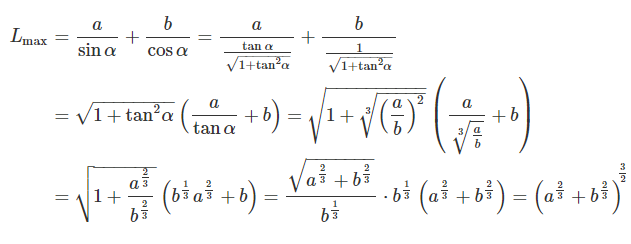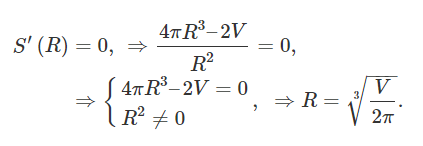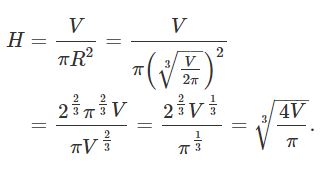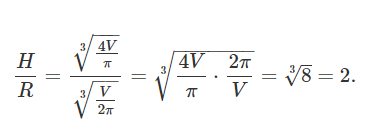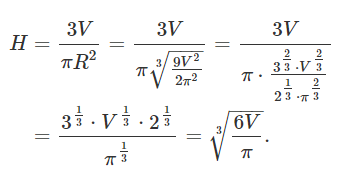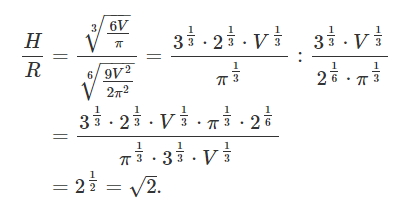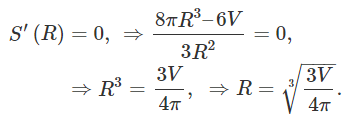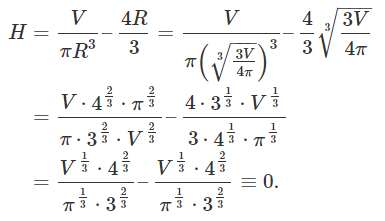در هندسه، مسائل مختلفی وجود دارد که در آنها میخواهیم بزرگترین یا کوچکترین مقدار یک تابع را پیدا کنیم. برای مثال، میتوانیم محیط یا مساحت یک شکل یا حجم یک جسم را به عنوان یک تابع در نظر بگیریم. در اینگونه مسائل بهینه سازی در هندسه میتوانیم یکی از پارامترهای شکل یا جسم هندسی (مثلاً طول یک ضلع یا زاویه بین دو ضلع) را به عنوان یک متغیر مستقل در نظر بگیریم. بعد از تشکیل تابع، باید مقادیر اکسترمم را با استفاده از مشتقگیری پیدا کنیم. باید توجه کنیم که توابع چنین مسائلی معمولاً در یک بازه کراندار تعریف میشوند که با هندسه سیستم و یا شرایط مسئله تعیین میگردند.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
مثالهای بهینه سازی در هندسه
در این بخش، مثالهای متنوعی را درباره کاربرد بهینهسازی در هندسه ارائه میکنیم.
مثال ۱
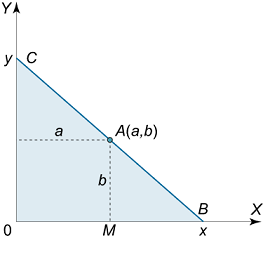
نقطه A ( a , b ) A\left( {a,b} \right) A ( a , b ) صفحه مختصات داده شده است. یک خط مستقیم رسم میکنیم که از این نقطه میگذرد و محورهای مختصات را در ربع اول قطع میکند. محلهای برخورد با محورها را به گونهای بیابید که مساحت مثلث تشکیل شده کمترین مقدار ممکن را داشته باشد (شکل ۱).
شکل ۱ حل: مثلثهای O B C OBC OBC M B A MBA MB A متشابه هستند. در نتیجه، رابطه زیر برقرار است:
O C M A = O B M B ⇒ y b = x x – a \large { \frac { { O C } } { { M A } } = \frac { { O B } }{ { M B } } \; \; } \kern0pt { \Rightarrow \; \; \frac { y } { b } = \frac { x } { { x – a } } } M A OC = MB OB ⇒ b y = x – a x
که در آن، مختصات x x x y y y x > a x > a x > a y > b y > b y > b y y y x x x
y = b x x – a . \large y = \frac { { b x } } { { x – a } } . y = x – a b x .
مساحت مثلث را با تابع S ( x ) S\left( x \right) S ( x )
S ( x ) = x y 2 = x 2 ⋅ b x x – a = b x 2 2 ( x – a ) . \large { S \left ( x \right ) = \frac { { x y } } { 2 } = \frac { x } { 2 } \cdot \frac { { b x } } { { x – a } } } = { \frac { { b { x ^ 2 } } } { { 2 \left ( { x – a } \right ) } } . } S ( x ) = 2 x y = 2 x ⋅ x – a b x = 2 ( x – a ) b x 2 .
مشتق تابع مساحت به صورت زیر است:
S ’ ( x ) = ( b x 2 2 ( x – a ) ) ′ = b 2 ( x 2 x – a ) ′ = b 2 ⋅ 2 x ( x – a ) – x 2 ( x – a ) 2 = b 2 ⋅ 2 x 2 – 2 a x – x 2 ( x – a ) 2 = b x ( x – 2 a ) 2 ( x – a ) 2 . \large \begin {align*} S ’ \left ( x \right ) & = { \left ( { \frac { { b { x ^ 2 } } }{ { 2 \left ( { x – a } \right ) } } } \right ) ^ \prime } = { \frac { b } { 2 } { \left ( { \frac { { { x ^ 2 } } } { { x – a } } } \right ) ^ \prime } } = { \frac { b } { 2 } \cdot \frac { { 2 x \left ( { x – a } \right ) – { x ^ 2 } } } { { { { \left ( { x – a } \right ) } ^ 2 } } } } \\ & = { \frac { b } { 2 } \cdot \frac { { 2 { x ^ 2 } – 2 a x – { x ^ 2 } } } { { { { \left ( { x – a } \right ) } ^ 2 } } } } = { \frac { { b x \left ( { x – 2 a } \right ) } } { { { { 2 \left ( { x – a } \right ) } ^ 2 } } } . } \end {align*} S ’ ( x ) = ( 2 ( x – a ) b x 2 ) ′ = 2 b ( x – a x 2 ) ′ = 2 b ⋅ ( x – a ) 2 2 x ( x – a ) – x 2 = 2 b ⋅ ( x – a ) 2 2 x 2 –2 a x – x 2 = 2 ( x – a ) 2 b x ( x –2 a ) .
تابع S ( x ) S\left( x \right) S ( x ) نقطه بحرانی x = 0 x = 0 x = 0 x = a x = a x = a x = 2 a x = 2a x = 2 a x > a x > a x > a x = 2 a x = 2 a x = 2 a x = 2 a x = 2a x = 2 a مینیمم تابع S ( x ) S (x ) S ( x )
ارتفاع مثلث برابر است با:
$$ \large \require {cancel} y = \frac { { b x } } { { x – a } } = \frac { { b \cdot 2 a } } { { 2 a – a } } = \frac { { 2 \cancel { a } b } } { \cancel { a } } = 2 b . $$
بنابراین، برای آنکه مساحت مثلث، کوچکترین مقدار باشد، باید ساقهای آن 2 a 2a 2 a 2 b 2b 2 b
مثال ۲
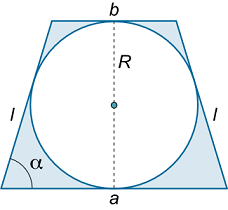
یک ذوزنقه متساوی الساقین، درون دایرهای به شعاع R R R α \alpha α
شکل ۲ حل: مساحت یک ذوزنقه متساوی الساقین، با رابطه زیر به دست میآید:
S T = a + b 2 ⋅ h \large { S _ T } = \frac { { a + b } } { 2 } \cdot h S T = 2 a + b ⋅ h
که در آن، a a a b b b h h h h = 2 R h = 2 R h = 2 R S K = π R 2 {S_K} = \pi {R^2} S K = π R 2
S = S T – S K = a + b 2 ⋅ 2 R – π R 2 = ( a + b ) R – π R 2 . \large { S = { S _ T } – { S _ K } } = { \frac { { a + b } } { 2 } \cdot 2 R – \pi { R ^ 2 } } = { \left ( { a + b } \right ) R – \pi { R ^ 2 } . } S = S T – S K = 2 a + b ⋅ 2 R – π R 2 = ( a + b ) R – π R 2 .
از آنجایی که ذوزنقه توسط دایره محاط شده است، مجموع دو ساق کناری برابر با مجموع قاعدهها است:
a + b = 2 ℓ or a + b = 2 ⋅ 2 R sin α = 4 R sin α . \large { a + b = 2 \ell \; \; \text {or} \; \; } \kern0pt { a + b = 2 \cdot \frac { { 2 R } } { { \sin \alpha } } } = { \frac { { 4 R } } { { \sin \alpha } } . } a + b = 2 ℓ or a + b = 2 ⋅ sin α 2 R = sin α 4 R .
که در آن، l l l ( a + b ) \left( {a + b} \right) ( a + b )
S = S ( α ) = 4 R sin α ⋅ R – π R 2 = R 2 ( 4 sin α – π ) . \large {S = S\left( \alpha \right) = \frac{{4R}}{{\sin \alpha }} \cdot R – \pi {R^2} } = {{R^2}\left( {\frac{4}{{\sin \alpha }} – \pi } \right).} S = S ( α ) = sin α 4 R ⋅ R – π R 2 = R 2 ( sin α 4 – π ) .
اکنون مشتق S ( α ) S\left( \alpha \right) S ( α )
S ’ ( α ) = [ R 2 ( 4 sin α – π ) ] ′ = 4 R 2 ( – 1 sin 2 α ) ⋅ cos α = – 4 R 2 cos α sin 2 α . \large \begin {align*} S’ \left ( \alpha \right ) & = { \left [ { { R ^ 2 } \left ( { \frac { 4 } { { \sin \alpha } } – \pi } \right ) } \right ] ^ \prime } \\ & = { 4 { R ^ 2 } \left ( { – \frac { 1 } { { { { \sin } ^ 2 } \alpha } } } \right ) \cdot \cos \alpha } = { – \frac { { 4 { R ^ 2 } \cos \alpha } } { { { { \sin } ^ 2 } \alpha } } . } \end {align*} S ’ ( α ) = [ R 2 ( sin α 4 – π ) ] ′ = 4 R 2 ( – sin 2 α 1 ) ⋅ cos α = – sin 2 α 4 R 2 cos α .
مشتق فوق، در حالت زیر برابر با صفر است:
cos α = 0 , ⇒ α = π 2 \large \cos \alpha = 0 , \; \; \Rightarrow \alpha = \frac { \pi }{ 2 } cos α = 0 , ⇒ α = 2 π
وقتی از این نقطه عبور کنیم (زاویه زیاد شود)، مشتق از منفی به مثبت تغییر خواهد کرد. در نتیجه، α = π 2 \alpha = \large\frac{\pi }{2}\normalsize α = 2 π S ( α ) S\left( \alpha \right) S ( α ) مربع تبدیل میشود. حداقل مقدار مساحت برابر است با:
S min = R 2 ( 4 – π ) . \large { S _ { \min } } = { R ^ 2 } \left ( { 4 – \pi } \right ) . S m i n = R 2 ( 4– π ) .
مثال ۳
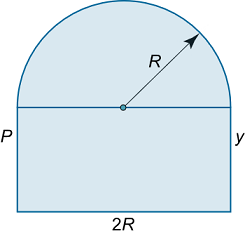
پنجرهای از یک مستطیل و نیمدایره تشکیل شده است (شکل ۳). محیط پنجره برابر با P P P R R R
شکل ۳ حل: واضح است که یک ضلع مستطیل برابر با 2 R 2R 2 R y y y
P = π R + 2 R + 2 y . \large P = \pi R + 2 R + 2 y . P = π R + 2 R + 2 y .
از رابطه بالا، y y y
y = 1 2 [ P – ( π + 2 ) R ] . \large y = \frac { 1 } { 2 } \left [ { P – \left ( { \pi + 2 } \right ) R } \right ] . y = 2 1 [ P – ( π + 2 ) R ] .
مساحت پنجره نیز برابر است با:
S = π R 2 2 + 2 R y = π R 2 2 + 2 R ⋅ 1 2 [ P – ( π + 2 ) R ] = π R 2 2 + P R – π R 2 – 2 R 2 = P R – π R 2 2 – 2 R 2 . \large \begin {align*} S & = \frac { { \pi { R ^ 2 } } } { 2 } + 2 R y = { \frac { { \pi { R ^ 2 } } } { 2 } + 2 R \cdot \frac { 1 } { 2 } \left [ { P – \left ( { \pi + 2 } \right ) R } \right ] } \\ & = { \frac { { \pi { R ^ 2 } } } { 2 } + P R – \pi { R ^ 2 } – 2 { R ^ 2 } } = { P R – \frac { { \pi { R ^ 2 } } } { 2 } – 2 { R ^ 2 } . } \end {align*} S = 2 π R 2 + 2 R y = 2 π R 2 + 2 R ⋅ 2 1 [ P – ( π + 2 ) R ] = 2 π R 2 + PR – π R 2 –2 R 2 = PR – 2 π R 2 –2 R 2 .
مساحت فوق، تابعی به صورت S ( R ) S\left( R \right) S ( R )
S ’ ( R ) = ( P R – π R 2 2 – 2 R 2 ) ′ = P – π R – 4 R = P – ( π + 4 ) R . \large \begin {align*} S’ \left ( R \right) & = \left ( P R – \frac { { \pi { R ^ 2 } } } { 2 } – 2 { R ^ 2 } \right ) ^ \prime \\ & = P – \pi R – 4 R = P – \left ( { \pi + 4 } \right ) R . \end {align*} S ’ ( R ) = ( PR – 2 π R 2 –2 R 2 ) ′ = P – π R –4 R = P – ( π + 4 ) R .
با صفر قرار دادن مشتق، داریم:
S ’ ( R ) = 0 , ⇒ P – ( π + 4 ) R = 0 , ⇒ R = P π + 4 . \large { S’ \left ( R \right ) = 0 , \; \; } \Rightarrow { P – \left ( { \pi + 4 } \right ) R = 0 , \; \; } \Rightarrow { R = \frac { P } { { \pi + 4 } } . } S ’ ( R ) = 0 , ⇒ P – ( π + 4 ) R = 0 , ⇒ R = π + 4 P .
مشتق دوم ، منفی است:
S ′ ′ ( R ) = [ P – ( π + 4 ) R ] ′ = – ( π + 4 ) < 0 \large { S ^ { \prime \prime } \left ( R \right ) = { \left [ { P – \left ( { \pi + 4 } \right ) R } \right ] ^ \prime } } = { – \left ( { \pi + 4 } \right ) \lt 0 } S ′′ ( R ) = [ P – ( π + 4 ) R ] ′ = – ( π + 4 ) < 0
در نتیجه، در نقطهای که به دست آوردیم، مساحت حداکثر است. این مقدار ماکزیمم برابر است با:
S max = P R – π R 2 2 – 2 R 2 = P ( P π + 4 ) – ( π 2 + 2 ) ( P π + 4 ) 2 = P 2 π + 4 – ( π + 4 ) P 2 2 ( π + 4 ) 2 = 2 P 2 – P 2 2 ( π + 4 ) = P 2 2 ( π + 4 ) . \large \begin {align*} { S _ { \max } } & = P R – \frac { { \pi { R ^2 } } } { 2 } – 2 { R ^ 2 } = { P \left ( { \frac { P } { { \pi + 4 } } } \right ) – \left ( { \frac { \pi } { 2 } + 2 } \right ) { \left ( { \frac { P } { { \pi + 4 } } } \right ) ^ 2 } } \\ & = { \frac { { { P ^ 2 } } }{ { \pi + 4 } } – \frac { { \left ( { \cancel { \pi + 4 } } \right ){ P ^ 2 } } } { { 2 { { \left ( { \pi + 4 } \right ) } ^ { \cancel { 2 } } } } } } = { \frac { { 2 { P ^ 2 } – { P ^ 2 } } } { { 2 \left ( { \pi + 4 } \right ) } } } = { \frac { { { P ^ 2 } } } { { 2 \left ( { \pi + 4 } \right ) } } . } \end {align*} S m a x = PR – 2 π R 2 –2 R 2 = P ( π + 4 P ) – ( 2 π + 2 ) ( π + 4 P ) 2 = π + 4 P 2 – 2 ( π + 4 ) 2 ( π + 4 ) P 2 = 2 ( π + 4 ) 2 P 2 – P 2 = 2 ( π + 4 ) P 2 .
مثال ۴
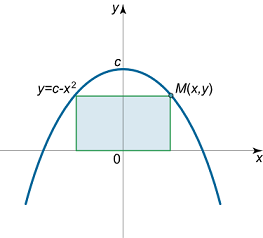
مستطیلی با اضلاع موازی با محورهای مختصات را در نظر بگیرید که یک ضلع آن روی محور x x x سهمی y = c – x 2 y = c – {x^2} y = c – x 2
حل: فرض کنید نقطه M ( x , y ) M\left( {x,y} \right) M ( x , y )
شکل ۴ طول اضلاع مستطیل، 2 x 2x 2 x 2 y 2y 2 y
S ( x ) = 2 x y = 2 x ( c – x 2 ) = 2 c x – 2 x 3 . \large { S \left ( x \right ) = 2 x y } = { 2 x \left ( { c – { x ^ 2 } } \right ) } = { 2 c x – 2 { x ^ 3 } . } S ( x ) = 2 x y = 2 x ( c – x 2 ) = 2 c x –2 x 3 .
برای یافتن نقطه اکسترمم، از S ( x ) S(x) S ( x )
S ’ ( x ) = ( 2 c x – 2 x 3 ) ′ = 2 c – 6 x 2 . \large S’ \left ( x \right ) = { \left ( { 2 c x – 2 { x ^ 3 } } \right ) ^ \prime } = 2 c – 6 { x ^ 2 } . S ’ ( x ) = ( 2 c x –2 x 3 ) ′ = 2 c –6 x 2 .
با برابر قرار دادن مشتق با صفر، داریم:
واضح است که هر دو ریشه، منجر به یک مقدار مساحت برابر خواهند شد. باید مطمئن شویم c 3 \sqrt {\large\frac{c}{3}\normalsize} 3 c S ( x ) S(x) S ( x )
S ′ ′ ( x ) = ( 2 c – 6 x 2 ) ′ = – 12 x < 0. \large S ^ { \prime \prime } \left ( x \right ) = { \left ( { 2 c – 6 { x ^ 2 } } \right ) ^ \prime } = – 1 2 x \lt 0 . S ′′ ( x ) = ( 2 c –6 x 2 ) ′ = –12 x < 0.
از آنجایی که S ′ ′ ( x ) < 0 S^{\prime\prime}\left( x \right) \lt 0 S ′′ ( x ) < 0 c 3 \sqrt {\large\frac{c}{3}\normalsize} 3 c
حداکثر مساحت مستطیل، برابر است با:
مثال ۵
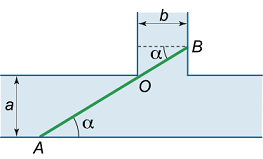
دو کانال با عرضهای a a a b b b
شکل ۵ فرض میکنیم موقعیت کشتی، مطابق شکل ۵ با زاویه α \alpha α L L L α \alpha α
L = ∣ A O ∣ + ∣ O B ∣ = a sin α + a cos α = L ( α ) . \large { L = \left | { A O } \right | + \left | { O B } \right | } = { \frac { a } { { \sin \alpha } } + \frac { a } { { \cos \alpha } } } = { L \left ( \alpha \right ) . } L = ∣ A O ∣ + ∣ OB ∣ = sin α a + cos α a = L ( α ) .
دو موقعیت اکسترمم به صورت زیر هستند:
α → 0 , ⇒ sin α → 0 , ⇒ ∣ A O ∣ → ∞ ; \large { \alpha \to 0 , \; \; } \Rightarrow { \sin \alpha \to 0 , \; \; } \Rightarrow { \left | { A O } \right | \to \infty ; } α → 0 , ⇒ sin α → 0 , ⇒ ∣ A O ∣ → ∞ ;
α → π 2 , ⇒ cos α → 0 , ⇒ ∣ O B ∣ → ∞ . \large { \alpha \to \frac { \pi } { 2 } , \; \; } \Rightarrow { \cos \alpha \to 0 , \; \; } \Rightarrow { \left | { O B } \right | \to \infty . } α → 2 π , ⇒ cos α → 0 , ⇒ ∣ OB ∣ → ∞.
در نتیجه، زاویه α \alpha α 0 < α < π 2 0 \lt \alpha \lt \large\frac{\pi }{2}\normalsize 0 < α < 2 π
اکنون مشتق تابع L ( α ) L\left( \alpha \right) L ( α )
L ’ ( α ) = ( – a sin 2 α ) ⋅ cos α – b cos 2 α ⋅ ( – sin α ) = b sin α cos 2 α – a cos α sin 2 α = b sin 3 α – a cos 3 α cos 2 α sin 2 α = 4 ( b sin 3 α – a cos 3 α ) sin 2 ( 2 α ) . \large \begin {align*} L’ \left ( \alpha \right ) & = \left ( { – \frac { a } { { { { \sin } ^ 2 } \alpha } } } \right ) \cdot \cos \alpha – \frac { b } { { { { \cos } ^ 2 } \alpha } } \cdot \left ( { – \sin \alpha } \right ) \\ & = { \frac { { b \sin \alpha } } { { { { \cos } ^ 2 } \alpha } } – \frac { { a \cos \alpha } } { { { \sin ^ 2 } \alpha } } } = { \frac { { b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha } }{ { { { \cos } ^ 2 } \alpha \, { { \sin } ^ 2 } \alpha } } } \\ & = { \frac { { 4 \left ( { b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha } \right ) } } { { { { \sin } ^ 2 } \left ( { 2 \alpha } \right ) } } . } \end {align*} L ’ ( α ) = ( – sin 2 α a ) ⋅ cos α – cos 2 α b ⋅ ( – sin α ) = cos 2 α b sin α – sin 2 α a cos α = cos 2 α sin 2 α b sin 3 α – a cos 3 α = sin 2 ( 2 α ) 4 ( b sin 3 α – a cos 3 α ) .
با صفر قرار دادن رابطه اخیر، داریم:
$$ \large \begin {align*}<br />
L’ \left ( \alpha \right ) & = 0 , \; \; \Rightarrow<br />
{ \frac { { 4 \left ( { b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha } \right ) } } { { { { \sin } ^ 2 } \left ( { 2 \alpha } \right ) } } = 0 , \; \; } \\ & \Rightarrow<br />
{ \left\{ { \begin {array} { * { 20 } { l } }<br />
{ b \, { { \sin } ^ 3 } \alpha – a \, { { \cos } ^ 3 } \alpha = 0 } \\<br />
{ { { \sin } ^ 2 } \left ( { 2 \alpha } \right ) \ne 0 }<br />
\end {array} } \right. , \; \; }\\ & \Rightarrow<br />
{ b \, { \tan ^ 3 } \alpha – a = 0, \; \; } \Rightarrow<br />
{ \tan \alpha = \sqrt [ \large 3 \normalsize ] { { \frac { a }{ b } } } . }<br />
\end {align*} $$
باید مطمئن شویم که وقتی از نقطه بحرانی α \alpha α L ( α ) L ( \alpha ) L ( α ) سینوس و کسینوس α \alpha α تانژانت مینویسیم:
1 + cot 2 α = 1 sin 2 α , ⇒ sin α = 1 1 + cot 2 α = 1 1 + 1 tan 2 α = tan α 1 + tan 2 α \large \begin {align*} 1 + { \cot ^ 2 } \alpha & = \frac { 1 } { { { { \sin } ^ 2 } \alpha } } , \; \; \\ \Rightarrow \sin \alpha & = \frac { 1 } { { \sqrt { 1 + { { \cot } ^ 2 } \alpha } }} \\ & = { \frac { 1 } { { \sqrt { 1 + \frac { 1 } { { { { \tan } ^ 2 } \alpha } } } } } } = { \frac { { \tan \alpha } } { { \sqrt { 1 + { { \tan } ^ 2 } \alpha } } } } \end {align*} 1 + cot 2 α ⇒ sin α = sin 2 α 1 , = 1 + cot 2 α 1 = 1 + t a n 2 α 1 1 = 1 + tan 2 α tan α
1 + tan 2 α = 1 cos 2 α , ⇒ cos α = 1 1 + tan 2 α . \large \begin {align*} { 1 + { \tan ^ 2 } \alpha = \frac { 1 } { { { \cos ^ 2 } \alpha } } , \; \; } \Rightarrow { \cos \alpha = \frac { 1 } { { \sqrt { 1 + { { \tan } ^ 2 } \alpha } } } . } \end {align*} 1 + tan 2 α = cos 2 α 1 , ⇒ cos α = 1 + tan 2 α 1 .
اکنون میتوانیم توصیف نهایی حداکثر طول ممکن کشتی را بنویسیم:
در یک حالت خاص، برای کانالهایی با عرض برابر (a = b a = b a = b
L max = ( 2 a 2 3 ) 3 = 8 a 2 = a 8 . \large \begin {align*} { { L _ { \max } } = \sqrt { { { \left ( { 2 { a ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ) } ^ 3 } } } = { \sqrt { 8 { a ^ 2 } } = a \sqrt 8 . } \end {align*} L m a x = ( 2 a 3 2 ) 3 = 8 a 2 = a 8 .
مثال ۶
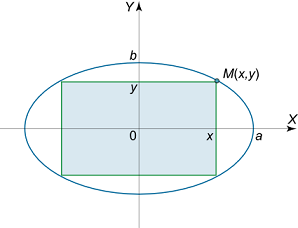
مستطیلی دارای اضلاعی موازی با محورهای مختصات است و درون یک بیضی محاط شده است (شکل ۶). معادله بیضی به صورت زیر است:
x 2 a 2 + y 2 b 2 = 1 \large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 a 2 x 2 + b 2 y 2 = 1
شکل ۶ فرض کنید نقطه M ( x , y ) M\left( {x,y} \right) M ( x , y )
S = 2 x ⋅ 2 y = 4 x y . \large S = 2 x \cdot 2 y = 4 x y . S = 2 x ⋅ 2 y = 4 x y .
کمیت y y y
x 2 a 2 + y 2 b 2 = 1 , ⇒ y 2 b 2 = 1 – x 2 a 2 , ⇒ y 2 = b 2 a 2 ( a 2 – x 2 ) , ⇒ y = ± b a a 2 – x 2 . \large \begin {align*} \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } & = 1 , \; \; \Rightarrow { \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 – \frac { { { x ^ 2 } } } { { { a ^ 2 } } } , \; \; } \\ & \Rightarrow { { y ^ 2 } = \frac { { { b ^ 2 } } } { { { a ^ 2 } } } \left ( { { a ^ 2 } – { x ^ 2 } } \right ) , \; \; } \\ & \Rightarrow { y = \pm \frac { b } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } . } \end {align*} a 2 x 2 + b 2 y 2 = 1 , ⇒ b 2 y 2 = 1– a 2 x 2 , ⇒ y 2 = a 2 b 2 ( a 2 – x 2 ) , ⇒ y = ± a b a 2 – x 2 .
در این مسئله، فقط مقادیر مثبت x x x y y y
S = 4 x y = 4 b x a a 2 – x 2 = S ( x ) . \large { S = 4 x y } = { \frac {{ 4 b x } } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } } = { S \left ( x \right ) . } S = 4 x y = a 4 b x a 2 – x 2 = S ( x ) .
برای یافتن اکسترمم، مشتق S ( x ) S(x) S ( x )
S ’ ( x ) = ( 4 b x a a 2 – x 2 ) ′ = 4 b a ⋅ [ a 2 – x 2 + x ⋅ 1 2 a 2 – x 2 ⋅ ( – 2 x ) ] = 4 b a [ a 2 – x 2 – x 2 a 2 – x 2 ] = 4 b a ⋅ a 2 – x 2 – x 2 a 2 – x 2 = 4 b ( a 2 – 2 x 2 ) a a 2 – x 2 . \large \begin {align*} S’ \left ( x \right ) & = { \left ( { \frac { { 4 b x } } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } } \right ) ^ \prime } = { \frac { { 4 b } } { a } \cdot } \kern0pt { \left [ { \sqrt { { a ^ 2 } – { x ^ 2 } } + x \cdot \frac { 1 } { { 2 \sqrt { { a ^ 2 } – { x ^ 2 } } } } \cdot \left ( { – 2 x } \right ) } \right ] } \\ & = { \frac { { 4 b } } { a } \left [ { \sqrt { { a ^ 2 } – { x ^ 2 } } – \frac { { { x ^ 2 } } } { { \sqrt { { a ^ 2 } – { x ^ 2 } } } } } \right ] } = { \frac { { 4 b } } { a } \cdot \frac { { { a ^ 2 } – { x ^ 2 } – { x ^ 2 } } } { { \sqrt { { a ^ 2 } – { x ^ 2 } } } } } = { \frac { { 4 b \left ( { { a ^ 2 } – 2 { x ^ 2 } } \right ) } } { { a \sqrt { { a ^ 2 } – { x ^ 2 } } } } . } \end {align*} S ’ ( x ) = ( a 4 b x a 2 – x 2 ) ′ = a 4 b ⋅ [ a 2 – x 2 + x ⋅ 2 a 2 – x 2 1 ⋅ ( –2 x ) ] = a 4 b [ a 2 – x 2 – a 2 – x 2 x 2 ] = a 4 b ⋅ a 2 – x 2 a 2 – x 2 – x 2 = a a 2 – x 2 4 b ( a 2 –2 x 2 ) .
اگر مشتق بالا را برابر با صفر قرار دهیم، داریم:
a 2 – 2 x 2 = 0 , ⇒ x 2 = a 2 2 , ⇒ x = a 2 . \large { { a ^ 2 } – 2 { x ^ 2 } = 0 , \; \; } \Rightarrow { { x ^ 2 } = \frac { { { a ^ 2 } } } { 2 } , \; \; } \Rightarrow { x = \frac { a } { { \sqrt 2 } } . } a 2 –2 x 2 = 0 , ⇒ x 2 = 2 a 2 , ⇒ x = 2 a .
وقتی از نقطه x = a 2 x = {\large\frac{a}{{\sqrt 2 }}\normalsize} x = 2 a
در نتیجه، مقدار y y y
y = b a a 2 – x 2 = b a a 2 – ( a 2 ) 2 = b a a 2 – a 2 2 = b a a 2 2 = b a ⋅ a 2 = b 2 . \large \begin {align*} y & = \frac { b } { a } \sqrt { { a ^ 2 } – { x ^ 2 } } = { \frac { b } { a } \sqrt { { a ^ 2 } – { { \left ( { \frac { a } { { \sqrt 2 } } } \right ) } ^ 2 } } } \\ &= { \frac { b } { a } \sqrt { { a ^ 2 } – \frac { { { a ^ 2 } } } { 2 } } } = { \frac { b } { a } \sqrt { \frac { { { a ^ 2 } } } { 2 } } } = { \frac { b } { a } \cdot \frac { a } { { \sqrt 2 } } } = { \frac { b } { { \sqrt 2 } } . } \end {align*} y = a b a 2 – x 2 = a b a 2 – ( 2 a ) 2 = a b a 2 – 2 a 2 = a b 2 a 2 = a b ⋅ 2 a = 2 b .
بنابراین، مستطیل محاط شده در بیضی، وقتی بیشترین مساحت ممکن را خواهد داشت که اضلاع آن به صورت زیر باشند:
2 x = 2 ⋅ a 2 = a 2 , 2 y = 2 ⋅ b 2 = b 2 . \large \begin {align*} { 2 x = 2 \cdot \frac { a } { { \sqrt 2 } } = a \sqrt 2 \; \text{, } \; \; \; \; } \kern-0.3pt { 2 y = 2 \cdot \frac { b } { { \sqrt 2 } } = b \sqrt 2 . } \end {align*} 2 x = 2 ⋅ 2 a = a 2 , 2 y = 2 ⋅ 2 b = b 2 .
حداکثر مقدار مساحت نیز برابر است با:
S max = a 2 ⋅ b 2 = 2 a b . \large { S _ { \max } } = a \sqrt 2 \cdot b \sqrt 2 = 2 a b . S m a x = a 2 ⋅ b 2 = 2 ab .
در حالت خاصی که محورهای بزرگ و کوچک بیضی برابر باشند (a = b = R a = b = R a = b = R
در این حالت، بزرگترین مساحت مستطیل، برابر است با:
R 2 \large R \sqrt 2 R 2
مثال ۷
تابلویی به ارتفاع a a a h h h x x x
شکل ۷ (الف) حل: واضح است که وقتی ناظر در وضعیت بهینه قرار دارد که، زاویه دید او حداکثر مقدار ممکن باشد.
ابتدا رابطه زاویه دید φ = ∠ B P A \varphi = \angle BPA φ = ∠ BP A
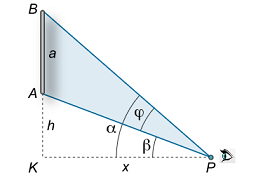
شکل ۷ (ب) طبق شکل ۷ (ب)، رابطه φ = α – β \varphi = \alpha – \beta φ = α – β
tan β = h x , tan α = a + h x . \large { \tan \beta = \frac { h } { x } , } \; \; \; \kern-0.3pt { \tan \alpha = \frac { { a + h } } { x } . } tan β = x h , tan α = x a + h .
با استفاده از اتحاد تانژانتِ تفاضلِ زاویهها داریم:
$$ \large \begin {align*}<br />
\require {cancel} \tan \varphi & = \tan \left ( {\alpha – \beta } \right ) = { \frac { { \tan \alpha – \tan \beta } } {{ 1 + \tan \alpha \tan \beta } } } \\<br />
& = { \frac { { \frac { { a + h } } { x } – \frac { h } { x } } } { { 1 + \frac { { a + h } } { x } \cdot \frac { h } { x } } } } = { \frac { { \frac { { a + \cancel { h } – \cancel { h } } } { x } } } { { \frac { { { x ^ 2 } + \left ( { a + h } \right ) h } } { { { x ^ 2 } } } } } } \\& = { \frac { { a x } } { { {x ^ 2 } + a h + { h ^ 2 } } } . }<br />
\end {align*} $$
بنابراین، میتوانیم عبارت زیر را برای تابع φ ( x ) \varphi \left( x \right) φ ( x )
φ = φ ( x ) = arctan a x x 2 + a h + h 2 . \large { \varphi = \varphi \left ( x \right ) } = { \arctan \frac { { a x } } { { { x ^ 2 } + a h + { h ^ 2 } } } . } φ = φ ( x ) = arctan x 2 + ah + h 2 a x .
مشتق این تابع برابر است با:
φ ′ ( x ) = ( arctan a x x 2 + a h + h 2 ) ′ = 1 1 + ( a x x 2 + a h + h 2 ) 2 ⋅ ( a x x 2 + a h + h 2 ) ′ = ( x 2 + a h + h 2 ) 2 ( x 2 + a h + h 2 ) 2 + ( a x ) 2 ⋅ a ( x 2 + a h + h 2 ) – a x ⋅ 2 x ( x 2 + a h + h 2 ) 2 + ( a x ) 2 = a x 2 + a 2 h + a h 2 – 2 a x 2 ( x 2 + a h + h 2 ) 2 + a 2 x 2 = a 2 h + a h 2 – a x 2 ( x 2 + a h + h 2 ) 2 + a 2 x 2 = a ( a h + h 2 – x 2 ) ( x 2 + a h + h 2 ) 2 + a 2 x 2 . \large \begin {align*} \varphi ^ \prime \left ( x \right ) & = { \left ( { \arctan \frac { { a x } } { { { x ^ 2 } + a h + { h ^ 2 } } } } \right ) ^ \prime } = { \frac { 1 } { { 1 + { { \left ( { \frac { { a x } }{ { { x ^ 2 } + a h + { h ^ 2 } } } } \right ) } ^ 2 } } } \cdot { \left ( { \frac { { a x } } { { { x ^ 2 } + a h + { h ^ 2 } } } } \right ) ^ \prime } } \\ &= { \frac { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { { \left ( { a x } \right ) } ^ 2 } } } }\kern0pt { \cdot \frac { { a \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) – a x \cdot 2 x } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { { \left ( { a x } \right ) } ^ 2 } } } } \\ & = { \frac { { a { x ^ 2 } + { a ^ 2 } h + a { h ^ 2 } – 2 a { x ^ 2 } } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 } { x ^ 2 } } } } = { \frac { { { a ^ 2 } h + a { h ^2 } – a { x ^ 2 } } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 } { x ^ 2 } } } } \\ &= { \frac { { a \left ( { a h + { h ^ 2 } – { x ^ 2 } } \right ) } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 } { x ^ 2 } } } . } \end {align*} φ ′ ( x ) = ( arctan x 2 + ah + h 2 a x ) ′ = 1 + ( x 2 + ah + h 2 a x ) 2 1 ⋅ ( x 2 + ah + h 2 a x ) ′ = ( x 2 + ah + h 2 ) 2 + ( a x ) 2 ( x 2 + ah + h 2 ) 2 ⋅ ( x 2 + ah + h 2 ) 2 + ( a x ) 2 a ( x 2 + ah + h 2 ) – a x ⋅ 2 x = ( x 2 + ah + h 2 ) 2 + a 2 x 2 a x 2 + a 2 h + a h 2 –2 a x 2 = ( x 2 + ah + h 2 ) 2 + a 2 x 2 a 2 h + a h 2 – a x 2 = ( x 2 + ah + h 2 ) 2 + a 2 x 2 a ( ah + h 2 – x 2 ) .
با صفر قرار دادن مشتق تابع بالا، داریم:
φ ′ ( x ) = 0 , ⇒ a ( a h + h 2 – x 2 ) ( x 2 + a h + h 2 ) 2 + a 2 x 2 = 0 , ⇒ a h + h 2 – x 2 = 0 , ⇒ x 2 = a h + h 2 , ⇒ x = h ( a + h ) . \large \begin {align*} \varphi ^ \prime \left ( x \right ) = 0 , \; \; & \Rightarrow { \frac { { a \left ( { a h + { h ^ 2 } – { x ^ 2 } } \right ) } } { { { { \left ( { { x ^ 2 } + a h + { h ^ 2 } } \right ) } ^ 2 } + { a ^ 2 }{ x ^ 2 } } } = 0 , \; \; } \\ & \Rightarrow { a h + { h ^ 2 } – { x ^ 2 } = 0 , \; \; } \\ & \Rightarrow { { x ^ 2 } = a h + { h ^ 2 } , \; \; } \Rightarrow { x = \sqrt { h \left ( { a + h } \right ) } .} \end {align*} φ ′ ( x ) = 0 , ⇒ ( x 2 + ah + h 2 ) 2 + a 2 x 2 a ( ah + h 2 – x 2 ) = 0 , ⇒ ah + h 2 – x 2 = 0 , ⇒ x 2 = ah + h 2 , ⇒ x = h ( a + h ) .
در این نقطه، φ ( x ) \varphi \left( x \right) φ ( x )
بنابراین، فاصله بهینه از دیوار برای بهترین زاویه دید از تصویر، با فرمول زیر به دست میآید:
x = h ( a + h ) . \large x = \sqrt { h \left ( { a + h } \right ) } . x = h ( a + h ) .
برای مثال، اگر a = 3 m a = 3\,\text{m} a = 3 m h = 2 m h = 2\,\text{m} h = 2 m
x = h ( a + h ) = 2 ( 3 + 2 ) = 10 ≈ 3.16 m . \large { x = \sqrt { h \left ( { a + h } \right ) } = \sqrt { 2 \left ( { 3 + 2 } \right ) } } = { \sqrt { 1 0 } \approx 3 . 1 6 \, \text {m} . } x = h ( a + h ) = 2 ( 3 + 2 ) = 10 ≈ 3.16 m .
مثال ۸
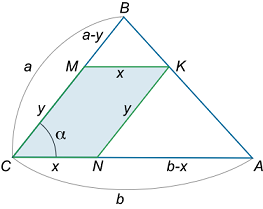
دو ضلع یک متوازی الاضلاع و یک رأس آن بر یک مثلث منطبق شدهاند (شکل ۸). در چه شرایطی مساحت این متوازی الاضلاع حداکثر مقدار ممکن است؟
شکل ۸ حل: مثلث را با دو ضلع a = B C a = BC a = BC b = A C b = AC b = A C α = ∠ B C A \alpha = \angle BCA α = ∠ BC A C M K N CMKN CM K N x = M K x = MK x = M K y = K N y = KN y = K N
S = x y sin α . \large S = xy\sin \alpha . S = x y sin α .
پارامتر y y y x x x a a a b b b
با توجه به تشابه مثلثهای B M K BMK BM K B C A BCA BC A
a – y a = x b . \large \frac { { a – y } } { a } = \frac { x } { b } . a a – y = b x .
در نتیجه، میتوان نوشت:
( a – y ) b = a x , ⇒ a b – b y = a x , ⇒ b y = a b – a x , ⇒ y = a b – a x b = a – a b x . \large \begin {align*} \left ( { a – y } \right ) b & = a x , \; \; \Rightarrow { a b – b y = a x , \; \; } \Rightarrow { b y = a b – a x , \; \; } \\ & \Rightarrow { y = \frac { { a b – a x } } { b } = a – \frac { a } { b } x . } \end {align*} ( a – y ) b = a x , ⇒ ab – b y = a x , ⇒ b y = ab – a x , ⇒ y = b ab – a x = a – b a x .
در نتیجه، مساحت S S S S ( x ) S(x) S ( x )
S = S ( x ) = x ( a – a b x ) sin α = a x sin α – a b x 2 sin α . \large \begin {align*} S & = S \left ( x \right ) = { x \left ( { a – \frac { a } { b } x } \right ) \sin \alpha } \\ & = { a x \sin \alpha – \frac { a } { b }{ x ^ 2 } \sin \alpha . } \end {align*} S = S ( x ) = x ( a – b a x ) sin α = a x sin α – b a x 2 sin α .
وقتی از این نقطه عبور میکنیم، مشتق از مثبت به منفی تغییر علامت میدهد و بنابراین، در آن، مقدار تابع حداکثر است. ضلع دیگر متوازی الاضلاع برابر است با:
y = a – a b x = a – a b ⋅ b 2 = a – a 2 = a 2 . \large \begin {align*} { y = a – \frac { a } { b } x = a – \frac { a } { b } \cdot \frac { b } { 2 } } = { a – \frac { a } { 2 } = \frac { a } { 2 } . } \end {align*} y = a – b a x = a – b a ⋅ 2 b = a – 2 a = 2 a .
بنابراین، متوازی الاضلاع با ضلعهای x x x y y y
x = b 2 , y = a 2 \large x = \frac { b } { 2 } , \; \; y = \frac { a } { 2 } x = 2 b , y = 2 a
مثال ۹
استوانهای را پیشنهاد دهید که مساحت سطح آن حداقل باشد.
حل: شکل بهینه یک استوانه با حجم ثابت، هزینه مواد به کار رفته در آن را کاهش میدهد. این مسئله در موارد مختلفی مانند مخزنهای ذخیره نفت مهم است (شکل ۹).
شکل ۹ فرض میکنیم H H H R R R
V = π R 2 H , S = 2 π R 2 + 2 π R H . \large { V = \pi { R ^ 2 } H , } \; \; \; \kern-0.3pt { S = 2 \pi { R ^ 2 } + 2 \pi R H . } V = π R 2 H , S = 2 π R 2 + 2 π R H .
شعاع قاعده R R R H H H V V V
H = V π R 2 . \large H = \frac { V } { { \pi { R ^ 2 } } } . H = π R 2 V .
میخواهیم مقدار اکسترمم تابع مساحت سطح S ( R ) S(R) S ( R )
S ( R ) = 2 π R 2 + 2 π R H = 2 π R 2 + 2 π R ⋅ V π R 2 = 2 π R 2 + 2 V R . \large \begin {align*} S \left ( R \right ) & = 2 \pi { R ^ 2 } + 2 \pi R H \\ &= { 2 \pi { R ^ 2 } + 2 \pi R \cdot \frac { V } { { \pi { R ^ 2 } } } } \\ & = { 2 \pi { R ^ 2 } + \frac { { 2 V } } { R } . } \end {align*} S ( R ) = 2 π R 2 + 2 π R H = 2 π R 2 + 2 π R ⋅ π R 2 V = 2 π R 2 + R 2 V .
مشتق تابع بالا برابر است با:
S ’ ( R ) = ( 2 π R 2 + 2 V R ) ′ = 4 π R – 2 V R 2 = 4 π R 3 – 2 V R 2 . \large { S’ \left ( R \right ) = { \left ( { 2 \pi { R ^ 2 } + \frac { { 2 V } } { R } } \right ) ^ \prime } } = { 4 \pi R – \frac {{ 2 V } } { { { R ^ 2 } } } } = { \frac { { 4 \pi { R ^ 3 } – 2 V } } { { { R ^ 2 } } } . } S ’ ( R ) = ( 2 π R 2 + R 2 V ) ′ = 4 π R – R 2 2 V = R 2 4 π R 3 –2 V .
با صفر قرار دادن این مشتق، داریم:
مقدار R R R S ( R ) S(R) S ( R )
در نتیجه، ارتفاع استوانه برابر خواهد بود با:
نسبت ارتفاع به شعاع قاعده، به صورت زیر است:
به عبارت دیگر، برای آنکه مساحت جانبی استوانه کوچکترین مقدار ممکن شود، باید ارتفاع آن برابر با قطر قاعده باشد.
مثال ۱۰
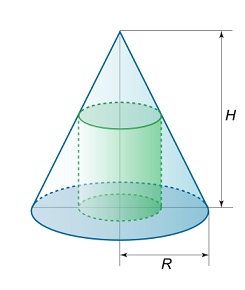
حداکثر حجم ممکن استوانهای را به دست آورید که در یک مخروط با ارتفاع H H H R R R
شکل ۱۰ (الف) حل: شعاع قاعده استوانه را با x x x y y y
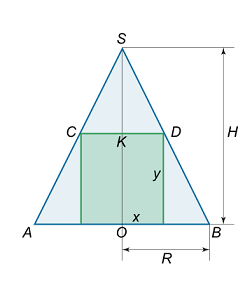
شکل ۱۰ (ب) با توجه به تشابه مثلثهای S K D SKD S KD S O B SOB SOB
K D O B = S K S O or x R = H – y H . \large { \frac { { K D } } { { O B } } = \frac { { S K } }{ { S O } } } \; \; \; \kern-0.3pt { \text {or} \; \; \; \frac { x } { R } = \frac { { H – y } } { H } .} OB KD = SO S K or R x = H H – y .
معادله اخیر، رابطه بین متغیرهای x x x y y y y y y x x x
x R = H – y H , ⇒ H X = ( H – y ) R , ⇒ H x = H R – R y , ⇒ y = H R – H x R = H ( 1 – x R ) . \large \begin {align*} \frac { x } { R } = \frac { { H – y } } { H } , \; \; & \Rightarrow { H X = \left ( { H – y } \right ) R , \; \; } \Rightarrow { H x = H R – R y , \; \; } \\ & \Rightarrow { y = \frac { { H R – H x } } { R } = H \left ( { 1 – \frac { x } { R } } \right ) . } \end {align*} R x = H H – y , ⇒ H X = ( H – y ) R , ⇒ H x = H R – R y , ⇒ y = R H R – H x = H ( 1– R x ) .
حجم محاط شده در استوانه با فرمول زیر بیان میشود:
V = π x 2 y . \large V = \pi { x ^ 2 } y . V = π x 2 y .
با نوشتن حجم بر حسب متغیر x x x
V ( x ) = π x 2 H ( 1 – x R ) = π H ( x 2 – x 3 R ) . \large { V \left ( x \right ) = \pi { x ^ 2} H \left ( { 1 – \frac { x } { R } } \right ) } = { \pi H\left ( { { x ^ 2 } – \frac { { { x ^ 3 } } } { R } } \right ) .} V ( x ) = π x 2 H ( 1– R x ) = π H ( x 2 – R x 3 ) .
برای به دست آوردن بزرگترین حجم ممکن، از تابع V ( x ) V(x) V ( x )
V ’ ( x ) = [ π H ( x 2 – x 3 R ) ] ′ = π H ( 2 x – 3 x 2 R ) ; \large \begin {align*} V’ \left ( x \right ) = { \left [ { \pi H \left ( { { x ^ 2 } – \frac { { { x ^ 3 } } } { R } } \right ) } \right ] ^ \prime } = { \pi H \left ( { 2 x – \frac { { 3 { x ^ 2 } } } { R } } \right ) ; } \end {align*} V ’ ( x ) = [ π H ( x 2 – R x 3 ) ] ′ = π H ( 2 x – R 3 x 2 ) ;
جواب x 1 = 0 {x_1} = 0 x 1 = 0 x 2 = 2 R 3 {x_2} = \large\frac{{2R}}{3}\normalsize x 2 = 3 2 R x = 2 R 3 x = \large\frac{{2R}}{3}\normalsize x = 3 2 R V ( x ) V(x) V ( x )
$$ \large \require {cancel} { y = H \left ( { 1 – \frac { x } { R } } \right ) } = { H \left ( { 1 – \frac { { 2 \cancel { R } } } { { 3 \cancel { R } } } } \right ) = \frac { H } { 3 } . } $$
در نتیجه، بزرگترین حجم ممکن برای استوانه محاط شده در مخروط، برابر خواهد بود با:
V max = π x 2 y = π ( 2 R 3 ) 2 ⋅ H 3 = 4 27 π R 2 H . \large { { V _ { \max } } = \pi { x ^ 2 } y } = { \pi { \left ( { \frac { { 2 R } } { 3 } } \right ) ^ 2 } \cdot \frac { H } { 3 } } = { \frac { 4 } { { 2 7 } } \pi { R ^ 2 } H . } V m a x = π x 2 y = π ( 3 2 R ) 2 ⋅ 3 H = 27 4 π R 2 H .
این مقدار، برابر با 4 9 \large\frac{4}{9}\normalsize 9 4
مثال ۱۱
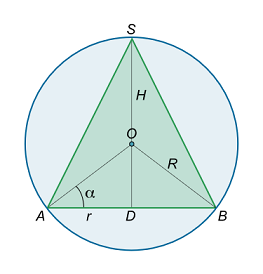
مشخصات مخروطی محاط در یک کره به شعاع R R R
حل: برش مقطعی مخروط محاط در کره در شکل ۱۱ نشان داده شده است.
شکل ۱۱ پارامتر H H H r r r α \alpha α
r = R cos α , H = R sin α + R . \large { r = R \cos \alpha , } \; \; \; \kern-0.3pt { H = R \sin \alpha + R . } r = R cos α , H = R sin α + R .
در این حالت، حجم مخروط را میتوان به صورت زیر نوشت:
V = 1 3 π r 2 H = 1 3 π ( R cos α ) 2 ( R sin α + R ) = 1 3 π R 3 cos 2 α ( sin α + 1 ) . \large \begin {align*} V & = \frac { 1 } { 3 } \pi { r ^ 2 } H = { \frac { 1 } { 3 } \pi { \left ( { R \cos \alpha } \right ) ^ 2 } \left ( { R \sin \alpha + R } \right ) } \\ & = { \frac { 1 } { 3 } \pi { R ^ 3 } { \cos ^ 2 } \alpha \left ( { \sin \alpha + 1} \right).} \end {align*} V = 3 1 π r 2 H = 3 1 π ( R cos α ) 2 ( R sin α + R ) = 3 1 π R 3 cos 2 α ( sin α + 1 ) .
که در آن، α \alpha α 0 < α < π 2 0 < \alpha < {\large\frac{\pi }{2}\normalsize} 0 < α < 2 π V V V α \alpha α
V ’ ( α ) = [ 1 3 π R 3 cos 2 α ( sin α + 1 ) ] ′ = 1 3 π R 3 [ cos 2 α ( sin α + 1 ) ] ′ = 1 3 π R 3 cos α ⋅ [ cos 2 α – 2 sin 2 α – 2 sin α ] ; \large \begin {align*} V’ \left ( \alpha \right ) & = { { \left [ { \frac { 1 } { 3 } \pi { R ^ 3 } { { \cos } ^ 2 } \alpha \left ( { \sin \alpha + 1 } \right ) } \right ] ^ \prime } } \\ &= { \frac { 1 } { 3 } \pi { R ^ 3 }{ \left [ { { { \cos } ^ 2 } \alpha \left ( { \sin \alpha + 1 } \right ) } \right ] ^ \prime } } \\ &= { { \frac { 1 } { 3 } \pi { R ^ 3 } \cos \alpha } \cdot \kern0pt { \left [ { { { \cos } ^ 2 } \alpha – 2 { { \sin } ^ 2 } \alpha – 2 \sin \alpha } \right ] } ; } \end {align*} V ’ ( α ) = [ 3 1 π R 3 cos 2 α ( sin α + 1 ) ] ′ = 3 1 π R 3 [ cos 2 α ( sin α + 1 ) ] ′ = 3 1 π R 3 cos α ⋅ [ cos 2 α –2 sin 2 α –2 sin α ] ;
مشتق بالا را برابر با صفر قرار میدهیم:
V ’ ( α ) = 0 , ⇒ 1 3 π R 3 cos α ⋅ [ cos 2 α – 2 sin 2 α – 2 sin α ] = 0. \large { V’ \left ( \alpha \right ) = 0 , \; \; } \Rightarrow { { \frac { 1 } { 3 } \pi { R ^ 3 } \cos \alpha } } \cdot \kern0pt { { \left [ { { { \cos } ^ 2 } \alpha – 2 { { \sin } ^ 2 } \alpha – 2 \sin \alpha } \right ] = 0 . } } V ’ ( α ) = 0 , ⇒ 3 1 π R 3 cos α ⋅ [ cos 2 α –2 sin 2 α –2 sin α ] = 0.
دو حالت مختلف رخ میدهد:
1 ) cos α = 0 , ⇒ α = π 2 ; \large { 1 ) \; \cos \alpha = 0 , \; \; } \Rightarrow { \alpha = \frac { \pi } { 2 } ; } 1 ) cos α = 0 , ⇒ α = 2 π ;
2 ) cos 2 α – 2 sin 2 α – 2 sin α = 0 , ⇒ 1 – 3 sin 2 α – 2 sin α = 0 , ⇒ 3 sin 2 α + 2 sin α – 1 = 0 , ⇒ sin α = t , ⇒ 3 t 2 + 2 t – 1 = 0 , ⇒ D = 4 – 4 ⋅ 3 ⋅ ( – 1 ) = 16 , ⇒ t 1 , 2 = – 2 ± 16 6 ; \large \begin {align*} & 2 ) \; { \cos ^ 2 } \alpha – 2 { \sin ^ 2 } \alpha – 2 \sin \alpha = 0 , \; \; \Rightarrow { 1 – 3 { \sin ^ 2 } \alpha – 2 \sin \alpha = 0 , \; \; } \\ & \Rightarrow { 3 { \sin ^ 2 } \alpha + 2 \sin \alpha – 1 = 0 , \; \; } \Rightarrow { \sin \alpha = t , \; \; } \Rightarrow { 3 { t ^ 2 } + 2 t – 1 = 0 , \; \; } \\ & \Rightarrow { D = 4 – 4 \cdot 3 \cdot \left ( { – 1 } \right ) = 1 6 , \; \; } \Rightarrow { { t _ { 1 , 2 } } = \frac { { – 2 \pm \sqrt { 1 6 } } } { 6 } ; \; \; } \end {align*} 2 ) cos 2 α –2 sin 2 α –2 sin α = 0 , ⇒ 1–3 sin 2 α –2 sin α = 0 , ⇒ 3 sin 2 α + 2 sin α –1 = 0 , ⇒ sin α = t , ⇒ 3 t 2 + 2 t –1 = 0 , ⇒ D = 4–4 ⋅ 3 ⋅ ( –1 ) = 16 , ⇒ t 1 , 2 = 6 –2 ± 16 ;
t 1 = – 1 , ⇒ sin α = – 1 , ⇒ α = 3 π 2 , t 2 = 1 3 , ⇒ sin α = 1 3 . \large \begin {align*} { t _ 1 } & = – 1 , \; \; \Rightarrow { \sin \alpha = – 1 , \; \; } \Rightarrow { \alpha = \frac { { 3 \pi } } { 2 } } , \\ { t _ 2 } & = \frac { 1 } { 3 } , \; \; \Rightarrow { \sin \alpha = \frac { 1 } { 3 } . } \end {align*} t 1 t 2 = –1 , ⇒ sin α = –1 , ⇒ α = 2 3 π , = 3 1 , ⇒ sin α = 3 1 .
همانطور که میبینیم، پاسخ مورد نظر sin α = 1 3 \sin \alpha = \large\frac{1}{3}\normalsize sin α = 3 1 α \alpha α
کسینوس زاویه α \alpha α
cos α = 1 – ( 1 3 ) 2 = 1 – 1 9 = 2 2 3 . \large { \cos \alpha = \sqrt { 1 – { { \left ( { \frac { 1 } { 3 } } \right ) } ^ 2 } } } = { \sqrt { 1 – \frac { 1 } { 9 } } = \frac { { 2 \sqrt 2 } } { 3 } .} cos α = 1– ( 3 1 ) 2 = 1– 9 1 = 3 2 2 .
در نتیجه، شعاع قاعده و ارتفاع مخروط متناظر با حجم حداکثر، به صورت زیر خواهند بود:
r = 2 2 3 R , H = R ⋅ 1 3 + R = 4 3 R . \large { r = \frac { { 2 \sqrt 2 } } { 3 } R , } \; \; \; \kern -0.3pt { { H = R \cdot \frac { 1 } {3 } + R } = { \frac { 4 }{ 3 } R . } } r = 3 2 2 R , H = R ⋅ 3 1 + R = 3 4 R .
حجم ماکزیمم نیز برابر است با:
V = 1 3 π r 2 H = π 3 ⋅ ( 2 2 3 ) 2 ⋅ 4 3 R = π 3 ⋅ 8 9 R 2 ⋅ 4 3 R = 32 81 π R 3 \large \begin {align*} V & = \frac { 1 } { 3 } \pi { r ^ 2 } H = { \frac { \pi } { 3 } \cdot { \left ( { \frac { { 2 \sqrt 2 } } { 3 } } \right ) ^ 2 } \cdot \frac { 4 } { 3 } R } \\ & = { \frac { \pi } { 3 } \cdot \frac { 8 } { 9 } { R ^ 2 } \cdot \frac { 4 } { 3 } R } = { \frac { { 3 2 } } { { 8 1 } } \pi { R ^ 3 } } \end {align*} V = 3 1 π r 2 H = 3 π ⋅ ( 3 2 2 ) 2 ⋅ 3 4 R = 3 π ⋅ 9 8 R 2 ⋅ 3 4 R = 81 32 π R 3
که 8 27 \large\frac{{8}}{{27}}\normalsize 27 8
مثال 12
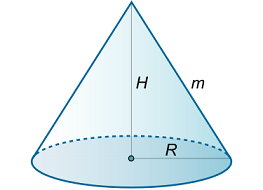
مخروطی به حجم V V V R R R H H H
حل: ارتفاع خمشی مخروط با m m m
شکل ۱۲ (الف) مساحت سطح جانبی با استفاده از فرمول زیر به دست میآید:
S L = π R m . \large { S _ { \text {L} } } = \pi Rm . S L = π R m .
در ادامه، برای سادگی، سطح جانبی را با S S S
V = 1 3 π R 2 H \large V = \frac { 1 } { 3 } \pi { R ^ 2 } H V = 3 1 π R 2 H
ارتفاع H H H R R R V V V
H = 3 V π R 2 . \large H = \frac { { 3 V } } { { \pi { R ^ 2 } } } . H = π R 2 3 V .
با استفاده از قضیه فیثاغورس ، داریم:
m = H 2 + R 2 = ( 3 V π R 2 ) 2 + R 2 . \large { m = \sqrt { { H ^ 2 } + { R ^ 2 } } } = { \sqrt { { { \left ( { \frac { { 3 V } } { { \pi { R ^ 2 } } } } \right ) } ^ 2 } + { R ^ 2 } } . } m = H 2 + R 2 = ( π R 2 3 V ) 2 + R 2 .
در ادامه، مساحت سطح جانبی را به صورت تابعی از شعاع قاعده R R R
S = π R m = π R ( 3 V π R 2 ) 2 + R 2 = π R 9 V 2 π 2 R 4 + R 2 = π R 9 V 2 + π 2 R 6 π 2 R 4 = π R π R 2 9 V 2 + π 2 R 6 = 9 V 2 + π 2 R 6 R . \large \begin {align*} S & = \pi R m = { \pi R \sqrt { { { \left ( { \frac { { 3 V } } { { \pi { R ^ 2 } } } } \right ) } ^ 2 } + { R ^ 2 } } } = { \pi R \sqrt { \frac { { 9 { V ^ 2 } } } { { { \pi ^ 2 } { R ^ 4 } } } + { R ^ 2 } } } \\ & = { \pi R \sqrt { \frac { { 9{ V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } { { { \pi ^ 2 } { R ^ 4 } } } } } = { \frac { { \cancel { \pi } \cancel { R } } } { { \cancel { \pi } { R ^ { \cancel { 2 } } } } } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } \\ & = { \frac { { \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } { R } . } \end {align*} S = π R m = π R ( π R 2 3 V ) 2 + R 2 = π R π 2 R 4 9 V 2 + R 2 = π R π 2 R 4 9 V 2 + π 2 R 6 = π R 2 π R 9 V 2 + π 2 R 6 = R 9 V 2 + π 2 R 6 .
مشتق این تابع، به صورت زیر است:
S ’ ( R ) = ( 9 V 2 + π 2 R 6 R ) ′ = 6 π 2 R 5 2 9 V 2 + π 2 R 6 ⋅ R – 9 V 2 + π 2 R 6 R 2 = 6 π 2 R 6 – 2 ( 9 V 2 + π 2 R 6 ) 2 R 2 9 V 2 + π 2 R 6 = 4 π 2 R 6 – 18 V 2 2 R 2 9 V 2 + π 2 R 6 = 2 π 2 R 6 – 9 V 2 R 2 9 V 2 + π 2 R 6 . \large \begin {align*} S’ \left ( R \right ) & = { { \left ( { \frac { { \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } { R } } \right ) ^ \prime } } = { \frac { { \frac { { 6 { \pi ^ 2 } { R ^ 5 } } } { { 2 \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } \cdot R – \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } { { { R ^ 2 } } } } \\ & = { \frac { { 6 { \pi ^ 2 } { R ^ 6 } – 2 \left ( { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } \right ) } } { { 2 { R ^ 2 } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } } = { \frac { { 4 { \pi ^ 2 }{ R ^ 6 } – 1 8 { V ^ 2 } } } { { 2 { R ^ 2 } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } } \\& = { \frac { { 2 { \pi ^ 2 } { R ^ 6 } – 9 { V ^ 2 } } } { { { R ^ 2 } \sqrt { 9 { V ^ 2 } + { \pi ^ 2 } { R ^ 6 } } } } .} \end {align*} S ’ ( R ) = ( R 9 V 2 + π 2 R 6 ) ′ = R 2 2 9 V 2 + π 2 R 6 6 π 2 R 5 ⋅ R – 9 V 2 + π 2 R 6 = 2 R 2 9 V 2 + π 2 R 6 6 π 2 R 6 –2 ( 9 V 2 + π 2 R 6 ) = 2 R 2 9 V 2 + π 2 R 6 4 π 2 R 6 –18 V 2 = R 2 9 V 2 + π 2 R 6 2 π 2 R 6 –9 V 2 .
با صفر قرار دادن مشتق بالا، داریم:
2 π 2 R 6 – 9 V 2 = 0 , ⇒ R 6 = 9 V 2 2 π 2 , ⇒ R = 9 V 2 2 π 2 6 . \large { 2 { \pi ^ 2 } { R ^ 6 } – 9 { V ^ 2 } = 0 , \; \; } \Rightarrow { { R ^ 6 } = \frac { { 9 { V ^ 2 } } } { { 2 { \pi ^ 2 } } } , \; \; } \Rightarrow { R = \sqrt [ \large 6 \normalsize ]{ { \frac { { 9 { V ^ 2 } } } { { 2 { \pi ^ 2 } } } } } . } 2 π 2 R 6 –9 V 2 = 0 , ⇒ R 6 = 2 π 2 9 V 2 , ⇒ R = 6 2 π 2 9 V 2 .
با افزایش R R R S ( R ) S(R) S ( R )
ارتفاع مخروط، برابر است با:
برای درک بهتر شکل بهینه مخروط، نسبت H R \large\frac{H}{R}\normalsize R H
بنابراین، ارتفاع مخروط برای آنکه مساحت سطح جانبی حداقل باشد، حدود 1.4 1.4 1.4
جالب است بدانید که نسبت ارتفاع به شعاع قاعده سازه غول پیکری به نام «مرکز تفریحی خانچادر» (Khan Shatyr Entertainment) مشابه عددی است که در این مثال به دست آوردیم.
شکل ۱۲ (ب) مثال ۱3
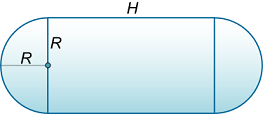
سطح مقطع جسمی مطابق شکل ۱۳ است. ارتفاع H H H R R R V V V
شکل ۱۳ حل: حجم برابر است با:
V = 4 3 π R 3 + π R 2 H = π R 2 ( 4 R 3 + H ) . \large { V = \frac { 4 } { 3 } \pi { R ^ 3 } + \pi { R ^ 2 } H } = { \pi { R ^ 2 } \left ( { \frac { { 4 R } } { 3 } + H } \right ) . } V = 3 4 π R 3 + π R 2 H = π R 2 ( 3 4 R + H ) .
ارتفاع را نیز به صورت زیر بیان میکنیم:
H = V π R 3 – 4 R 3 . \large H = \frac { V } { { \pi { R ^ 3 } } } – \frac { { 4 R } } { 3 } . H = π R 3 V – 3 4 R .
کل مساحت جسم نیز برابر است با:
S = 4 π R 2 + 2 π R H . \large S = 4 \pi { R ^ 2 } + 2 \pi R H . S = 4 π R 2 + 2 π R H .
با جایگذاری عبارت H H H
S = S ( R ) = 4 π R 2 + 2 π R ( V π R 3 – 4 R 3 ) = 4 π R 2 + 2 V R – 8 π R 2 3 = 4 π R 2 3 + 2 V R . \large \begin {align*} S & = S \left ( R \right ) = { 4 \pi { R ^ 2 } + 2 \pi R \left ( { \frac { V } { { \pi { R ^ 3 } } } – \frac { { 4 R } } {3 } } \right ) } \\ &= { 4 \pi { R ^ 2 } + \frac { { 2 V } } { R } – \frac { { 8 \pi { R ^ 2 } } } { 3 } } = { \frac { { 4 \pi { R ^ 2 } } } { 3 } + \frac { { 2 V } } { R } .} \end {align*} S = S ( R ) = 4 π R 2 + 2 π R ( π R 3 V – 3 4 R ) = 4 π R 2 + R 2 V – 3 8 π R 2 = 3 4 π R 2 + R 2 V .
اکنون مشتق S ( R ) S(R) S ( R )
S ’ ( R ) = ( 4 π R 2 3 + 2 V R ) ′ = 4 π 3 ⋅ 2 R – 2 V R 2 = 8 π R 3 – 2 V R 2 = 8 π R 3 – 6 V 3 R 2 . \large \begin {align*} S’ \left ( R \right ) & = { { \left ( { \frac { { 4 \pi { R ^ 2 } } } { 3 } + \frac { { 2 V } } { R } } \right ) ^ \prime } } = { \frac { { 4 \pi } } { 3 } \cdot 2 R – \frac { { 2 V } } { { { R ^ 2 } } } } \\ &= { \frac { { 8 \pi R } } { 3 } – \frac { { 2 V } } { { { R ^ 2 } } } } = { \frac { { 8 \pi { R ^ 3 } – 6 V } } {{ 3 { R ^ 2 } } } . } \end {align*} S ’ ( R ) = ( 3 4 π R 2 + R 2 V ) ′ = 3 4 π ⋅ 2 R – R 2 2 V = 3 8 π R – R 2 2 V = 3 R 2 8 π R 3 –6 V .
در نتیجه، نقطه اکسترمم به صورت زیر خواهد بود:
واضح است که در نقطه بالا، تابع کمینه میشود. اکنون ارتفاع متناظر با این مقدار را محاسبه میکنیم:
همانطور که میبینیم، شکل مورد نظر، باید کرهای بدون بخش استوانهای باشد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش کاربرد بهینه سازی در هندسه – به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی کاربرد بهینهسازی در هندسه فیلم آموزشی حل چند مثال از کاربرد بهینهسازی در هندسه