سیکل رانکین (Rankine Cycle) – یادگیری با مثال

«سیکل رانکین» (Rankine Cycle) یا «سیکل بخار رانکین» به مجموعه‌ فرآیند‌های بسته‌ای گفته می‌شود که نتیجه آن کار مفید خروجی است. معمولا در این سیکل‌ها از آب به‌عنوان سیال کاری استفاده می‌شود. هم‌چنین در بخشی از فرآیند‌های این سیکل، سیال مذکور به صورت بخار و در بخشی دیگر به شکل مایع است.

عمدتا از سیکل رانکین برای تولید توان در نیروگاه‌های مبتنی بر سوخت فسیلی یا هسته‌ای استفاده می‌شود. در این نیروگاه‌ها با استفاده از سوزاندن سوخت‌های مذکور، آب را در بویلر - یا دیگ بخار - به بخار تبدیل می‌کنند. پس از آن، با عبور دادن این بخار از توربین، کار مدنظر تولید می‌شود. شکل زیر شماتیک کارکرد سیکل رانکین را نشان می‌دهد.

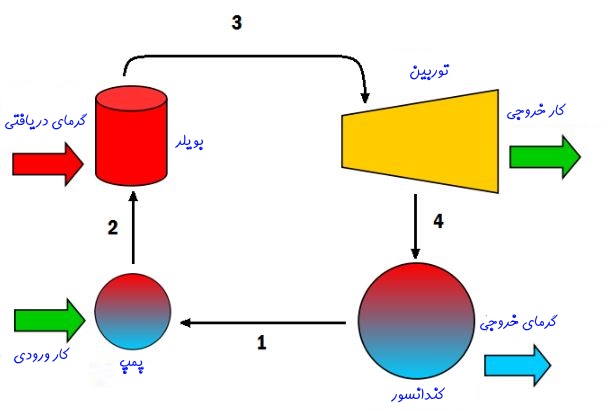
فرآیند‌های انجام شده در یک سیکل رانکین

در حالت کلی ۴ فرآیند اصلی در یک سیکل رانکین اتفاق می‌افتد. در ادامه هرکدام از این فرآیند‌ها توضیح داده شده:

• ۲→۱: افزایش فشار سیال با استفاده از پمپ
• ۳→۲: انتقال حرارت به سیال پرفشار توسط بویلر و تبدیل آن به بخار داغ
• ۴→۳: انبساط بخار در توربین و تولید کار
• ۱→۴: خنک و متراکم شدن سیال در کندانسور

با توجه به مراحل بالا متوجه شدیم که یک سیکل ایده‌آل رانکین از ۴ عنصر پمپ، بویلر، توربین و کندانسور تشکیل شده است. در ادامه در مورد روابط حاکم بر این فرآیند‌ها توضیح خواهیم داد.

به‌منظور توضیح دقیق فرآیند‌های رخ داده در یک سیکل رانکین، دو شکل زیر را در نظر بگیرید.

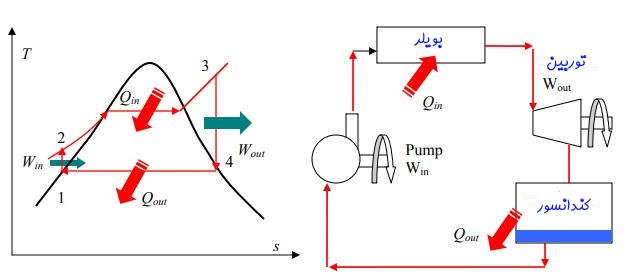
در این سیکل فرآیند‌ها به ترتیب زیر اتفاق می‌افتند.

• ۲→۱: آیزنتروپیک
• ۳→۲: فشار ثابت
• ۴→۳: آیزنتروپیک
• ۱→۴: فشار ثابت

با توجه به مفاهیم عنوان شده به‌منظور تحلیل سیکل رانکین در ابتدا بایستی مقدار حرارت و کار مبادله شده با محیط را در هر مرحله یافت. توجه کنید که در این تحلیل h نشان دهنده آنتالپی ویژه سیال در هر مرحله است.

پمپ (فرآیند ۲→۱)

در ابتدا پمپ روی سیال کار انجام داده و فشار آن را افزایش می‌دهد. با فرض این‌که کار انجام شده و انتقال حرارت صورت گرفته را با w_pump,in و q نشان دهیم و با توجه به این‌که این فرآیند به صورت آیزنتروپیک انجام می‌شود، می‌توان برای این فرآیند قانون اول ترمودینامیک را به صورت زیر نوشت:

w_pump,in + q = h₂ - h₁

در سیکل رانکین ایده‌آل توربین و پمپ به صورت عایق در نظر گرفته می‌شوند، از این رو مقدار انتقال حرارت خالص صورت گرفته برابر با صفر است. در نتیجه رابطه بالا به شکل زیر در خواهد آمد.

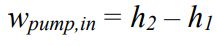
با توجه به این که سیال ورودی و خروجی به پمپ، به صورت مایع است، بنابراین چگالی آن تقریبا ثابت فرض می‌شود. اگر حجم ویژه (یا همان چگالی) سیال را با نماد ν نشان دهیم، تغییرات آنتالپی در فرآیند ۲-۱ را می‌توان به صورت زیر محاسبه کرد.

$$h_2-h_1=\Delta h= p_2 \nu_2 - p_1 \nu_1=(p_2 - p_1){\nu}$$

در ادامه از رابطه بالا بیشتر استفاده خواهیم کرد.

بویلر (فرآیند ۳→۲)

همان‌طور که در بالا نیز بیان کردیم، انتقال حرارت صورت گرفته به سیال در بویلر، به صورت فشار ثابت است. هماننند تحلیل پمپ، در این‌جا نیز با استفاده از قانون اول که در زیر بیان شده، می‌توان مقدار حرارت منتقل شده به سیال را بدست آورد. توجه داشته باشید که در این مرحله q_in میزان حرارت وارد شده به سیال را نشان می‌دهد. بنابراین می‌توان گفت:

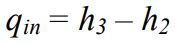
در شکل ۱، نقطه ۳ وضعیت سیال را پس از خروج از بویلر نشان می‌دهد. همان‌طور که می‌توان دید در این نقطه آب به صورت بخار «فوق گرم» (Super Heat) است.

توربین (فرآیند ۴→۳)

در توربین است که کار خروجی تولید می‌شود. همانند پمپ، سیال در توربین فرآیندی آیزنتروپیک را تجربه می‌کند. توجه داشته باشید که تمامی این گزاره‌ها مربوط به حالتی است که با یک سیکل ایده‌آل رانکین روبرو هستیم. با توجه به مفاهیم بیان شده، قانون اول برای این فرایند را می‌توان به شکل زیر بیان کرد:

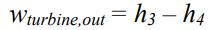
در رابطه بالا w_turbine,out کار خروجی توربین را نشان می‌دهد. توجه کنید که در این جا نمی‌توان هم‌چون پمپ کار را به طور مستقیم محاسبه کرد. بنابراین بایستی آنتالپی ویژه مربوط جریان ورودی و خروجی از توربین خوانده شود و در معادله بالا قرار گیرد.

کندانسور (فرآیند ۱→۴)

احتمالا حدس زده‌اید که این مرحله نیز شبیه به مرحله بویلر است. تفاوتشان در این است که در بویلر سیال گرم و در کندانسور سرد می‌شود. قانون اول برای این مرحله به صورت زیر است.

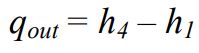
راندمان سیکل رانکین

همانند دیگر سیکل‌های ترمودینامیکی در این سیکل نیز با تقسیم کار خالص خروجی از سیکل و حرارت ورودی به آن، راندمان سیکل محاسبه می‌شود. برای بدست آوردن کار خالص خروجی می‌توان گفت:

$$w_{net}=w_{turbine}-w_{pump}=(h_{3}-h_{4})-(h_{2}-h_{1})$$

توجه داشته باشیدکه کار خروجی مثبت و کار ورودی منفی در نظر گرفته می‌شود. به همین دلیل است که در رابطه بالا قبل از کار پمپ از علامت منفی استفاده کرده‌ایم. از طرفی برای بدست آوردن راندمان بایستی میزان حرارت وارد شده به سیکل را نیز محاسبه کنیم. همان‌طور که می‌دانید در سیکل رانکین این بویلر است که به سیستم انرژی می‌دهد. در نتیجه انرژی وارد شده به سیکل برابر است با:

$$q_{in}=q _ { Boiler}=h_{3}-h_{2}$$

بنابراین با تقسیم کار خالص خروجی به حرارت ورودی به سیکل، می‌توان راندمان سیکل رانکین را به شکل محاسبه کرد.

$$\eta = \frac {w_{net}}{q_{in}}=\frac {(h_{3}-h_{4})-(h_{2}-h_{1})}{(h_{3}-h_{2})}$$

مثال

سیکلی مبتنی بر رانکین را مطابق شکل زیر تصور کنید. این سیکل به صورت ایده‌آل در نظر گرفته شده و در آن از بازیاب گرمایی استفاده نشده است.

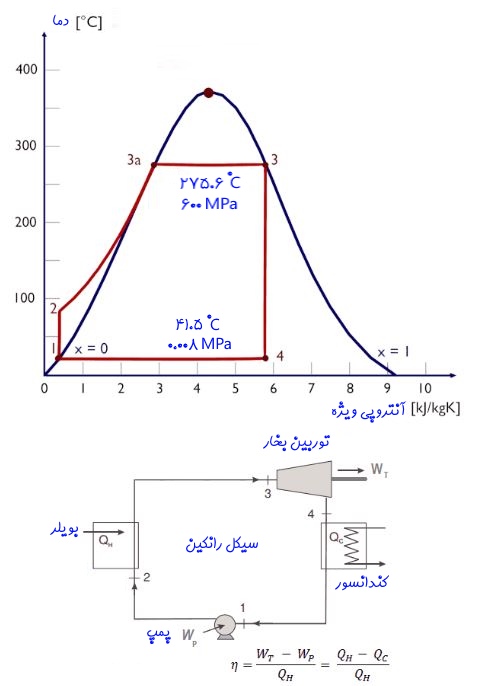
فرض کنید سیال ورودی به توربین در دمای ۲۷۵.۶ درجه و فشار ۶ مگاپاسکال است. سیال ورودی کاملا به شکل بخار است. بخشی از سیال پس از منبسط شدن در توربین به صورت مایع در می‌آید. در این حالت چند درصد از سیال خروجی از توربین را بخار تشکیل می‌دهد؟ فرض کنید سیال در دما و فشار ۴۱.۵ درجه و ۰.۰۰۸ مگاپاسکال از توربین خارج می‌شود. با این فرض موارد زیر را محاسبه کنید.

• کیفیت بخار خروجی از توربین
• کار انجام شده توسط توربین
• حرارت اضافه شده به سیستم
• راندمان ترمودینامیکی این سیکل

فیلم آموزش ترمودینامیک مهندسی شیمی ۲ – مرور و حل مساله در فرادرس

کلیک کنید

در ترمودینامیک برای سیالی که ترکیبی از بخار و مایع است، کمیتی تحت عنوان کیفیت تعریف می‌شود. این کمیت درصد تشکیل‌دهنده بخار را در یک ترکیب مایع و بخار نشان می‌دهد. برای مثال با توجه به تعریف انجام شده، کیفیت سیال ورودی به پمپ، صفر درصد و کیفیت بخار خروجی از بویلر ۱۰۰ درصد است.

از آنجایی که مقدار دقیق کیفیت بخار خروجی را نمی‌دانیم، در اولین قدم بایستی این مجهول یافت شود. با توجه به معلوم بودن فشار خروجی از توربین، می‌توان آنتروپی مربوط به بخار اشباع و آنتروپی مربوط به مایع اشباع را از جدول خواص ترمودینامیکی خواند. ‌‌از طرفی می‌دانیم که مقدار آنتروپی ترکیب مایع و بخار اشباع را می‌توان به شکل زیر بیان کرد.

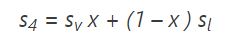
با توجه به این که فشار خروجی توربین برابر با فشار ورودی به پمپ است (به شکل ۱ نگاه کنید) بنابراین خواص ترمودینامیکی نقطه ۴ را می‌توان در فشار ۰.۰۰۸ مگاپاسکال (که همان فشار ورودی است) و از جدول خواص ترمودینامیکی برداشت. دلیل این کار برابر بودن فشار دو نقطه اشباعِ ۱ و ۴ است.

اجزاء معادله بالا به شرح زیر هستند.

• s₄=5.89 kj/kgk: آنتروپی ترکیب بخار و مایع در نقطه ۴
• s_v=8.227 kj/kgk: آنتروپی بخار خالص در نقطه ورود به توربین (نقطه ۳)
• s_l=0.592 kj/kgk: آنتروپی مربوط به مایع اشباع در نقطه ۱

با جایگذاری این مقادیر در معادله ۱ کیفیت بخار خروجی از توربین به صورت زیر بدست می‌آید.

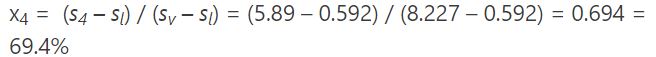
با استفاده از کیفیت بدست آمده می‌توان معادله ۱ را برای آنتالپی نوشت. هم‌چنین آنتالپی بخار و مایع اشباع را از جدول خواص ترمودینامیکی، در فشار ۰.۰۰۸ مگاپاسکال می‌خوانیم. با مراجعه به جدول مقادیر h_4v و h_4l به ترتیب برابر با ۲۵۷۶ و ۰.۶۹۴ کیلوگرم/کیلوژول خوانده می‌شوند. بنابراین آنتالپی کل نقطه ۴ را می‌توان به شکل زیر محاسبه کرد.

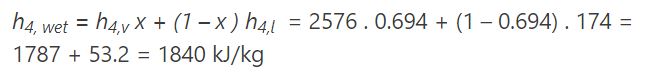
از طرفی می‌دانیم که سیال ورودی به توربین به صورت بخار اشباع است. بنابراین می‌توان آنتالپی این نقطه را از جدول خواص ترمودینامیکی برداشت. نهایتا مقدار h₃ برابر با ۲۷۸۵ خوانده می‌شود. با معلوم شدن مقادیر h₃ و h₄ و هم‌چنین با استفاده از قانون اول ترمودینامیک کار خروجی از توربین نیز به صورت زیر بدست می‌آید.

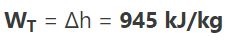
توجه داشته باشید که فرآیند‌های یک سیکل رانکین در حالت واقعی دارای بازگشت‌ناپذیری هستند. بنابراین فرآیند‌های رخ داده در پمپ و توربین ممکن است به صورت بازگشت ناپذیر بوده و آنتروپی تولید کنند. از طرفی  فرآیند انتقال حرارت نیز به صورت دقیقا فشار ثابت نیست و در بویلر و کندانسور افت فشاری وجود خواهد داشت. هم‌چنین به منظور افزایش راندمان این سیکل از روشی تحت عنوان «بازگرمایش» استفاده می‌کنند.

انحراف از سیکل ایده‌آل رانکین

همان‌طور که در بالا نیز بیان کردیم، در یک سیکل ترمودینامیکی واقعی به دلیل وجود برگشت‌ ناپذیری‌ها فرآیند‌ی که کاملا به صورت آدیاباتیک، فشار ثابت یا آیزنتروپیک باشد، رخ نخواهد داد. از این رو به منظور تحلیل چنین سیکل‌هایی آن را با استفاده از تقریب خاصی با سیکل‌های واقعی مدل‌سازی می‌کنند.

اجازه دهید در قدم اول مقادیر ثابتی را به منظور توصیف این برگشت‌ناپذیری‌ها تعریف کنیم. از این رو دو مفهوم «راندمان آیزنتروپیک» را برای پمپ و توربین به صورت زیر تعریف می‌کنیم.

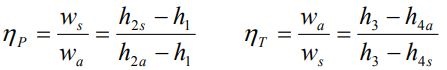
در رابطه بالا اندیس‌های a نشان دهنده مقادیر واقعی (مثلا h_a مقدار واقعی آنتالپی را در نقطه a نشان می‌دهد) خواص ترمودینامیکی و اندیس s مقادیر ایده‌آل را نشان می‌دهند.

شکل زیر سیکل رانکین را در دو حالت ایده‌آل و هم‌چنین در حالت وجود برگشت‌ناپذیری در توربین و پمپ را نشان می‌دهد. در این شکل نمودار قرمز رنگ، سیکل ایده‌آل رانکین و نمودار مشکی رنگ، سیکل واقعی رانکین را نشان می‌دهند.

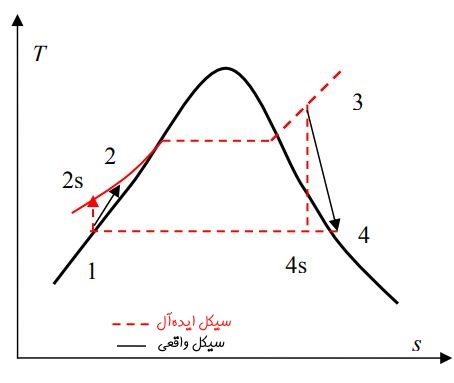
مثال

شکل ۲ نیروگاهی را نشان می‌دهد که مبتنی بر سیکل رانکین کار می‌کند.

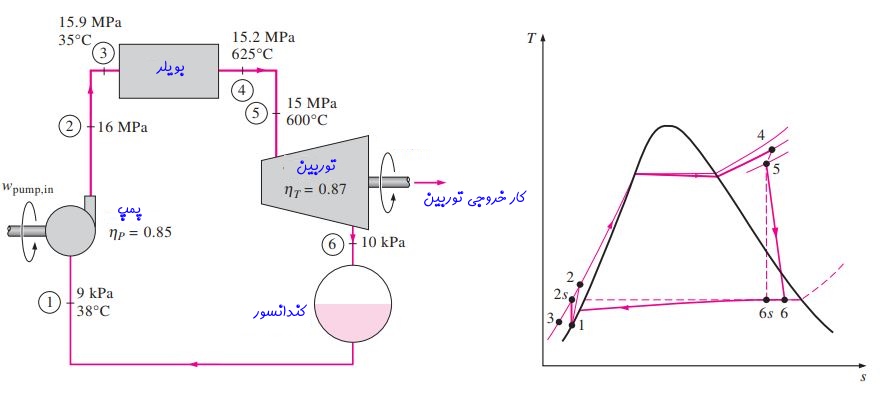
احتمالا همان‌طور که متوجه شده‌اید، می‌توان از نمودار دید که این سیکل از حالت ایده‌آل منحرف شده. راندمان آیزنتروپیک توربین و پمپ را به ترتیب برابر با ۸۷ و ۸۵ درصد در نظر بگیرید. با فرض این‌که نرخ جریان جرمی در این سیکل برابر با ۱۵ کیلوگرم بر ثانیه باشد، موارد زیر مطلوب است:

• بازده حرارتی این سیکل
• کار خالص خروجی از سیکل

پیشنهاد می‌کنیم برای حل مسائل مربوط به سیکل رانکین مسیر فرآیند‌ها را روی نمودار مربوط به آن در نظر بگیرید. در حقیقت با نگاهی اولیه به نمودار می‌توان فهمید که کدام خواص را داریم و کدام‌یک از آن‌ها مجهول هستند.

داده‌های اولیه مسئله را می‌توانید روی نمودار T-S مشاهده کنید. در هر نقطه مقادیر دما و فشار مشخص شده‌اند. اولین قدم برای حل این مسئله این است که کار خالص خروجی از سیستم را بیابیم. بدین منظور می‌توان با استفاده از تعریف راندمان پمپ و توربین در ابتدا مقادیر کار ایده‌آل آن‌ها را محاسبه کرد سپس با اعمال راندمانشان، مقادیر واقعی کار پمپ و توربین را یافت. بنابراین می‌توان گفت:

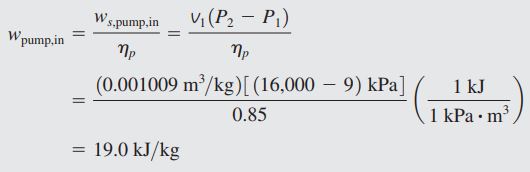
به همین صورت کار توربین نیز برابر است با:

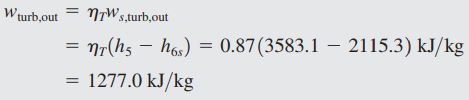
گرمای اضافه شده به سیال را مطابق با حالت سیکل ایده‌آل می‌توان یافت و تفاوتی در این حالت وجود ندارد. در نتیجه داریم:

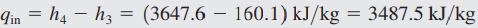
نهایتا با بدست آمدن کار خالص خروجی و گرمای داده شده به سیکل، راندمان حرارتی سیکل را طبق تعریف و به شکل زیر محاسبه می‌کنیم.

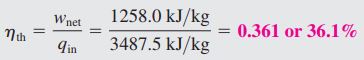
مقادیر گرما و کار محاسبه شده بر واحد جرم هستند. از این رو برای بدست آوردن مقادیر مطلق آن‌ها بایستی اعداد محاسبه شده را در دبی جریان ضرب کرد. برای نمونه کار خالص بدست آمده توسط این سیکل را می‌توان به شکل زیر بدست آورد.

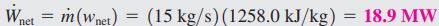
از روش‌هایی که به منظور افزایش راندمان سیکل‌های حرارتی استفاده می‌شود، «بازگرمایش» (Reheating) است. در بخشی مجزا در مورد این روش بحث خواهیم کرد.

در این مطلب مفاهیم اصلی و پایه‌ای مربوط به سیکل توانی رانکین را مورد بررسی قرار دادیم. البته مفاهیم مربوط به سیکل‌های ترمودینامیکی نیازمند تمرین بسیار و حل سئوالات گوناگون است. در این‌جا مثال‌های متفاوتی در مورد سیکل‌های ترمودینامیکی حل شده است که می‌تواند برای تسلط به موضوع برایتان مفید باشد.

^^