محاسبات ریاضی با تابع های داخلی PHP — به زبان ساده

عملیات مختلف ریاضیات مقدماتی به صورت مکرر در زمان برنامهنویسی مورد نیاز هستند. در این موارد، هنگام نوشتن کد باید به طور مکرر مقادیر مختلف را مقایسه، جمع، ضرب، تفریق و تقسیم بکنیم. برخی اوقات عملیات ریاضی مورد نیاز در یک برنامه بسیار پیچیدهتر از این است. در این موارد باید بتوانید با لگاریتمها، مثلثات یا تابعهای نمایی کار بکنید. در این راهنما به بررسی شیوه استفاده از هر یک از تابع های داخلی PHP به همراه ارائه مثالها میپردازیم.
این راهنما به معرفی تابعهای داخلی ریاضیاتی PHP برای اجرای محاسبات مثلثاتی، نمایی و لگاریتمی اختصاص دارد. همچنین به بررسی روش گرد کردن اعداد و ایجاد اعداد تصادفی میپردازیم.
تابعهای مثلثاتی در PHP
در زبان برنامهنویسی PHP با استفاده از تابعهای (sin($angle)، cos($angle و (tan($angle میتوان به ترتیب سینوس، کسینوس و تانژانت زوایای مختلف را که بر اساس رادیان بیان شدهاند پیدا کرد. همه این تابعها مقادیر float بازمیگردانند و مقدار دریافتی آنها باید زاویه بر مبنای رادیان باشد.
این بدان معنی است که وقتی مقدار (tan(45 را محاسبه کنیم، مقدار 1 به دست میآید، زیرا در واقع ما مشغول محاسبه مقدار تانژانت 45 رادیان هستیم که حدود 2.578 درجه خواهد بود. خوشبختانه PHP دو تابع بسیار مفید برای تبدیل رادیان به درجه و برعکس دارد. این تابعها به ترتیب ()rad2deg و ()deg2rad هستند. بنابراین اگر بخواهید عملاً مقدار تانژانت 45 درجه را محاسبه کنید، میتوانید کد آن را به صورت ((tan(deg2rad(45 بنویسید.
لازم به ذکر است که هیچ تابع مستقیم PHP برای محاسبه مقدار ()cosec()، sec یا ()cot وجود ندارد. با این وجود، این مقادیر مرتبط با مقادیر ()sin()، cos و ()tan هستند و از این رو میتوانید آنها را همچنان به طور غیر مستقیم محاسبه کنید.
همچنین میتوانید حالت عکس را استفاده کنید و زاویهای که یک مقدار مثلثاتی خاص دارد را بیابید. این تابعها به نام ()asin()، acos و ()atan خوانده میشوند. نکتهای که باید به خاطر داشته باشید این است که مقادیر سینوس و کسینوس هرگز برای هیچ زاویهای نمیتوانند از محدوده 1- تا 1 فراتر بروند. این بدان معنی است که مقادیر ورودی برای تابعهای ()asin و ()acos صرفاً در محدوده 1- تا 1 معتبر خواهند بود و مقداری خارج از این بازه مقدار تعریف نشده بازگشت میدهد.
مثلثات کاربردهای زیادی مانند تعیین خط سیر یک پرتابه یا ارتفاع و مسافت شیءهای مختلف دارد و از این رو دسترسی به این تابعها در صورتی که کدی برای شبیهسازی برخی موقعیتهای فیزیکی مینویسید کاملاً مفید خواهد بود.
این تابعها ضمناً در مواردی که میخواهید عناصر مختلف را با استفاده از مقادیر شعاعی و زاویهای ترسیم کنید کاملاً مفید خواهند بود. فرض کنید میخواهید یک الگو از دایرههای مختلف پیرامون یک دایره بزرگتر در مسافتی یکنواخت رسم کنید. میدانیم که ترسیم هر شکل نیازمند ارسال مختصات آن به صورت x و y است؛ اما ترسیم الگوهای دایرهای با استفاده از مختصات قطبی سادهتر است.
در این حالت با بهرهگیری از تابعهای مثلثاتی میتوانید شکلهای موردنظر را با استفاده از ()sin و ()cos برای تبدیل به مختصات دکارتی رسم کنید. در ادامه مثالی برای این حالت ارائه شده است:
1<?php
2
3$image = imagecreatetruecolor(800, 600);
4$bg = imagecolorallocate($image, 255, 255, 255);
5imagefill($image, 0, 0, $bg);
6
7$radius = 80;
8
9for($i = 0; $i < 12; $i++) {
10 $col_ellipse = imagecolorallocate($image, rand(0, 200), rand(0, 200), rand(0, 200));
11
12 imagefilledellipse($image, 175 + 125*cos(deg2rad($i*30)), 175 + 125*sin(deg2rad($i*30)), 3*$radius/4, 3*$radius/4, $col_ellipse);
13 imageellipse($image, 175 + 125*cos(deg2rad($i*30)), 175 + 125*sin(deg2rad($i*30)), 3.5*$radius/4, 3.5*$radius/4, $col_ellipse);
14
15 $col_ellipse = imagecolorallocate($image, rand(0, 200), rand(0, 200), rand(0, 200));
16
17 imagefilledellipse($image, 575 + 150*cos(deg2rad($i*30)), 375 + 150*sin(deg2rad($i*30)), 3*$radius/4, 3*$radius/4, $col_ellipse);
18 imageellipse($image, 575 + 150*cos(deg2rad($i*30)), 375 + 150*sin(deg2rad($i*30)), 3.5*$radius/4, 3.5*$radius/4, $col_ellipse);
19}
20
21$col_ellipse = imagecolorallocate($image, 255, 255, 255);
22imagefilledellipse($image, 175, 175, 275, 275, $col_ellipse);
23
24?>تصویر زیر نتیجه نهایی کد PHP فوق را نشان میدهد:
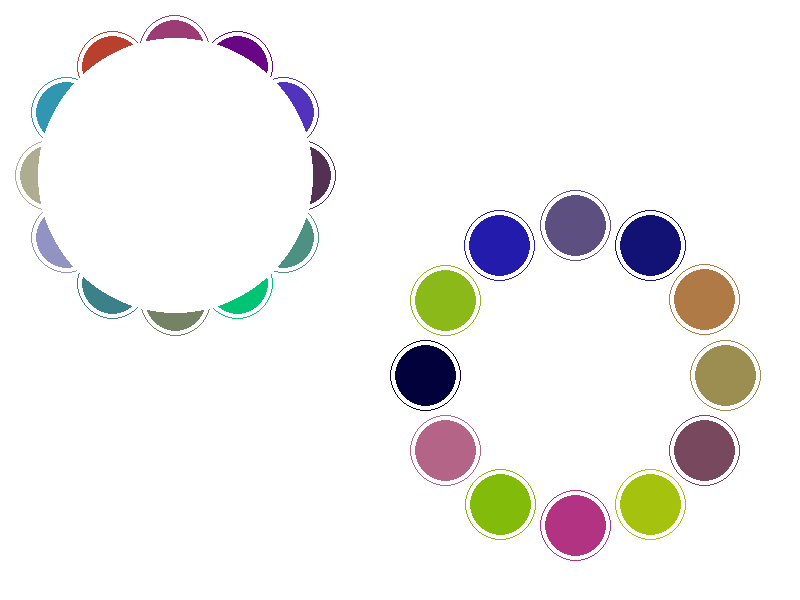
تابعهای نمایی و لگاریتمی
PHP برخی تابعهای نمایی و لگاریتمی نیز دارد. تابع (exp($value مقدار ثابت e را که به توان مقدار اعشاری value$ رسیده است بازگشت میدهد. به طور مشابه، میتوانید لگاریتم یک عدد مفروض را با استفاده از (log($arg, $base به هر پایهای محاسبه کنید. اگر base$ نادیده گرفته شود، این لگاریتم با استفاده از پایه طبیعی e محاسبه خواهد شد. اگر بخواهید لگاریتم یک عدد را در مبنای 10 محاسبه کنید، میتوانید به سادگی از تابع (log10($arg استفاده کنید.
یک تابع دیگر که ممکن است مفید باشد، (pow($base, $exp است که مقدار base$ را به توان exp$ رسانده و بازگشت میدهد. البته برخی افراد ممکن است استفاده از عملگر ** را ترجیح دهند. عبارت a**$b$ همان نتیجه تابع (pow($a, $b را به دست میدهد. با این وجود، با استفاده از این عبارت ممکن است در برخی موقعیتها نتیجه نادرستی به دست آورید. برای نمونه 0.5**1- نتیجه 1- به دست میدهد که نادرست است. محاسبه همین عبارت با استفاده از (pow(-1, 0.5 مقدار صحیح یعنی NaN را ارائه میکند.
1<?php
2
3echo log(1000, M_E); // 6.9077552789821
4echo log(1000); // 6.9077552789821
5echo log(1000, 10); // 3
6echo log10(1000); // 3
7
8echo pow(121, -121); // 9.6154627930786E-253
9echo pow(121, 121); // 1.0399915443694E+252
10echo pow(121, 1331); // INF
11
12?>برخی تابعهای مفید دیگر ریاضیاتی در PHP
در ادامه برخی از تابعهای مفید ریاضیاتی دیگری که در PHP وجود دارند را ارائه کردهایم.
گرد کردن اعداد
تابعهای ریاضیاتی مهم دیگری نیز وجود دارند. شما میتوانید کسرها یا اعداد اعشاری را با استفاده از تابع (ceil(float $value تا نزدیکترین عدد صحیح بزرگتر گرد کنید. به این ترتب هر دو عدد 2.1 و 2.9 به عدد 3 گرد میشوند. به طور مشابه میتوانید تابعها یا اعداد اعشاری را با استفاده از تابع (floor(float $value تا نزدیکترین عدد صحیح به سمت پایین گرد کنید. بدین ترتیب اعداد 2.1 و 2.9 به عدد 2 گرد میشوند.
این تابعها برای گرد کردن آسان نتایج محاسبههای متفاوت مناسب هستند. فرض کنید بخواهیم محاسبه کنیم یک سالن بر اساس مساحتش پذیرای چند نفر میتواند باشد. پاسخ نهایی پس از تقسیم احتمالاً یک عدد اعشاری خواهد بود؛ اما شما نمیتوانید افراد را به صورت کسری تقسیم کنید، بنابراین پاسخ صحیح مقدار کف مقدار محاسبه شده خواهد بود.
در اغلب موارد میخواهیم که یک عدد را به سمت بالا یا پایین؛ هر کدام که نزدیکتر باشد، به یک عدد صحیح گرد کنیم. برای نمونه میخواهیم عدد 2.1 به عدد 2 گرد شود؛ اما همزمان عدد 2.9 به عدد 3 گرد شود. این کار از طریق تابع (round($value, $precision, $mode به سهولت ممکن است. پارامتر precision$ تعداد ارقام اعشاری که باید گرد شوند را تعیین میکند. مقدار پیشفرض 0 است که یعنی اعداد صحیح بازگشت میدهد. پارامتر سوم به صورت mode$ برای تعیین حالتی استفاده میشود که عدد ورودی مورد نظر برای گرد کردن دقیقاً در میانه دو عدد بالا و پایین قرار داشته باشد. بدین ترتیب میتوان تعیین کرد که میخواهیم 3.5 به 3 یا 4 گرد شود.
کمینه و بیشینه
PHP دو تابع به نامهای (min($values و (max($values نیز دارند که به تعیین کمترین و بزرگترین مقادیر در یک مجموعه یا آرایه از اعداد کمک میکند. این تابعها م توانند انواع مختلفی از پارامترها مانند دو آرایه و یک رشته نیز بپذیرند. برای کسب اطلاع بیشتر در مورد شیوه مقایسه این تابعها میتوانید به مستندات آنها (+) مراجعه کنید.
1<?php
2
3$hall_width = 120;
4$hall_length = 180;
5$per_person_area = 35;
6
7$hall_capacity = floor($hall_length*$hall_length/$per_person_area);
8
9// Output: The hall can only accommodate 925 people.
10echo 'The hall can only accommodate '.$hall_capacity.' people.';
11
12$water_tank_volume = 548733;
13$bucket_volume = 305;
14
15$buckets_needed = ceil($water_tank_volume/$bucket_volume);
16
17// Output: We will need 1800 buckets of water to completely fill the tank.
18echo 'We will need '.$buckets_needed.' buckets of water to completely fill the tank.';
19
20$marks = [49, 58, 93, 12, 30];
21
22// Output: Minimum and maximum obtained marks in the exam are 12 and 93 respectively.
23echo 'Minimum and maximum obtained marks in the exam are '.min($marks).' and '.max($marks).' respectively.';
24?>تقسیم صحیح
در PHP میتوان با استفاده از تابع (intdiv($dividend, $divisor تقسیم صحیح نیز انجام داد. در این حالت تنها بخش صحیح خارجقسمت پس از تقسیم بازگشت مییابد. به طور مشابه میتوانید باقیمانده یا پیمانه را نیز پس از تقسیم دو آرگومان با استفاده از تابع (fmod($dividend, $divisor به دست آورید. مقدار بازگشتی همواره کمتر از divisor$ خواهد بود.
تابعهای مفید دیگری مانند (is_nan($value)، is_finite($value و (is_infinite($val نیز وجود دارند که میتوان برای تعیین عدد بودن یک مقدار و این که در صورت عدد بودن، آیا متناهی یا نامتناهی است، استفاده کرد. به یاد داشته باشید که PHP هر مقداری را که نتواند در یک نوع داده float بگنجاند، نامتناهی تصور میکند. بنابراین تابع ()is_finite برای مقدار 100 فاکتوریل نتیجه true بازمیگرداند؛ اما در مورد 1000 فاکتوریل آن را نامتناهی میداند.
ایجاد اعداد تصادفی در PHP
اعداد تصادفی در برخی موقعیتها کاملاً مفید هستند. میتوان از آنها برای ایجاد دادههای «تصادفی» برای اپلیکیشن یا پراکنده ساختن عناصر دشمن در یک بازی و موارد دیگر استفاده کرد. همواره باید به خاطر داشته باشید که هیچ یک از تابعهایی که در این بخش برسی میکنیم، اعداد تصادفی که از نظر رمزنگاری امن باشند تولید نمیکنند. این تابعها تنها به منظور استفاده در موقعیتهایی که امنیت مهم نیست، مانند ایجاد متن تصادفی خوشامدگویی برای بازدیدکنندگان تکراری یا استفاده برای تولید دادههای آماری مناسب هستند.
تابعهای (rand($min, $max و (mt_rand($min, $max میتوانند اعداد صحیح تصادفی مثبت بین مقادیر مفروض شامل min$ و max$ تولید کنند. زمانی که تابعها بدون هیچ پارامتری فراخوانی شوند، اعداد تصادفی بین 0 و ()getrandmax ایجاد میکنند. شما میتوانید مقدار ()getrandmax را ()echo کنید تا بیشینه عدد ممکن که این تابعها میتوانند روی پلتفرم شما تولید کنند را مشاهده کنید.
تابع ()mt_rand به میزان 4 برابر سریعتر از ()rand است و در صورتی که max$ کمتر از min$ باشد، مقدار false بازگشت میدهد. از نسخه 7.1.0 PHP به بعد، تابع ()rand در واقع نام مستعاری برای ()mt_rand محسوب میشود. تنها تفاوت این دو آن است که ()rand همچنان در صورتی که max$ کمتر از min$ باشد، خطایی صادر نمیکند تا سازگاری رو به عقب آن حفظ شود.
در ادامه یک حلقه را ملاحظه میکنید که یک میلیون بار اعداد تصادفی بین 0 و 100 ایجاد میکند. همان طور که میبینید مقادیر 0، 50 و 100 با نوسان اندکی تقریباً 10،000 بار تولید شدهاند.
1<?php
2
3$rand_values = [];
4$sum = 0;
5$count = 1000000;
6
7for($i = 0; $i < $count; $i++) {
8 $rand_values[$i] = mt_rand(0, 100);
9 $sum += $rand_values[$i];
10}
11
12$count_frequency = array_count_values($rand_values);
13
14// Output: 100 was randomly generated 9969 times.
15echo '100 was randomly generated '.$count_frequency[100].' times.';
16
17// Output: 50 was randomly generated: 9994 times.
18echo '50 was randomly generated: '.$count_frequency[50].' times.';
19
20// Output: 0 was randomly generated: 10010 times.
21echo '0 was randomly generated: '.$count_frequency[0].' times.';
22
23// Output: Average of random values: 49.97295
24echo 'Average of random values: '.($sum/$count);
25
26?>هر دو این تابعها، تابعهای seeder خاص خود را نیز دارند که ()srand و ()mt_srand نامیده میشوند و یک بذر (seed) برای تولیدکنندههای عدد تصادفی ارائه میکنند. باید به خاطر بسپارید که تنها کافی است یک بار ()srand و ()mt_srand را در برنامه خود فراخوانی کنید. فراخوانی آنها پیش از هر فراخوانی ()rand و ()mt_rand باعث میشود که هر بار همان اعداد تصادفی قبلی را دریافت کنید.
1
2<?php
3
4srand(215);
5echo rand()."\n"; // 330544099
6srand(215);
7echo rand()."\n"; // 330544099
8srand(215);
9echo rand()."\n"; // 330544099
10echo rand()."\n"; // 138190029
11echo rand()."\n"; // 1051333090
12echo rand()."\n"; // 1219572487
13
14?>سخن پایانی
PHP دارای تابعهای داخلی زیادی است که میتوانند نیازهای محاسباتی روزمره ما را رفع کنند. میتوان از این تابعها برای انجام کارهای پیچیدهتری مانند یافتن «بزرگترین مقسومعلیه مشترک»، «کوچکترین مضرب مشترک» و فاکتوریل استفاده کرد.
چند چیز وجود دارند که باید هنگام استفاده از این تابعها به خاطر داشته باشید. برای مثال، مقدار بازگشتی از تابعهایی مانند ()floor و ()ceil یک عدد صحیح است؛ اما همچنان نوع داده آن float است. به طور مشابه، همه تابعهای مثلثاتی انتظار دارند که زاویههایی که ارائه میکنید در مقیاس رادیان باشند. در صورتی که زاویه را با مقیاس درجه به آنها بدهید، ممکن است نتایجی برخلاف انتظار از آنها بگیرید. بنابراین برای اطمینان بیشتر، مقدار بازگشتی و آرگومانهای مورد انتظار این تابع را در مستندات PHP (+) بررسی کنید.
اگر این نوشته برای شما مفید بوده است، پیشنهاد ما استفاده از آموزشهای زیر است:
- مجموعه آموزشهای برنامهنویسی
- گنجینه برنامه نویسی PHP
- مجموعه آموزش های برنامه نویسی PHP
- آرایه های PHP — به زبان ساده
- آموزش فریمورک لاراول PHP Laravel برای ساخت فروشگاه اینترنتی
- آموزش پروژه محور PHP — مجموعه مقالات جامع وبلاگ فرادرس
- برنامهنویسی PHP و هر آنچه برای شروع باید بدانید — آموزش جامع
==










