کنترل مد لغزشی – به زبان ساده
«کنترل مد لغزشی» (Sliding Mode Control) یا SMC یک روش کنترل غیرخطی است که ویژگیهای منحصر به فردی مانند دقت، قوام، و تنظیم و پیادهسازی آسان دارد.
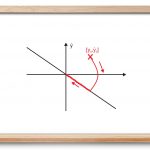
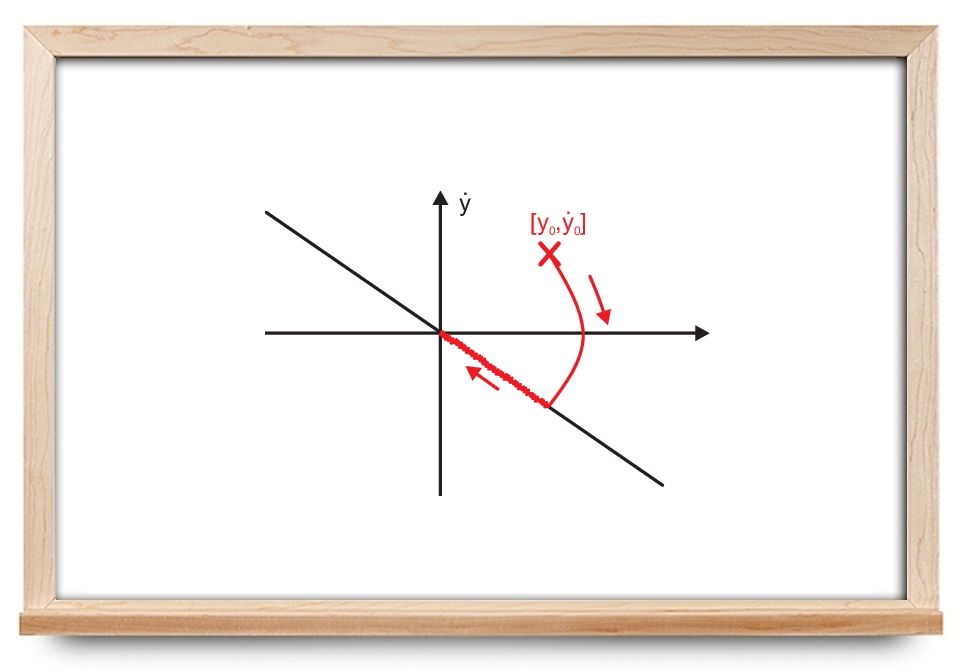
به طور خلاصه میتوان گفت که در کنترل مد لغزشی حالتهای سیستم به یک سطح، به نام «سطح لغزش» (Sliding Surface)، در فضای حالت برده میشوند. وقتی حالتها به سطح لغزش رسیدند، کنترل مد لغزشی حالتها را در نزدیکی و همسایگی سطح لغزش نگه میدارد. بنابراین، این رویکرد، یک روش کنترلی با دو بخش است. در بخش اول یک سطح لغزش طراحی میشود که حرکت لغزشی مشخصات طراحی را برآورده کند. در بخش دوم، قانون کنترلی انتخاب میشود که با آن، سطح سوئیچنگ حالت سیستم را جذب کند.
کنترل مد لغزشی دو مزیت اصلی دارد. اولین مزیت این است که میتوان با انتخاب تابع لغزشی مناسب، به رفتار دینامیکی مطلوب سیستم دست یافت. مزیت دوم این است که پاسخ حلقهبسته سیستم هیچ حساسیتی نسبت به نامعینیها (پارامترهای مدل، اغتشاشها و غیرخطی بودن) ندارد. در نتیجه، از دیدگاه عملی، با استفاده از کنترل مد لغزشی میتوانیم فرایندهای غیرخطی را در حضور اغتشاشات و نامعینیهای مدل کنترل کنیم.
کنترل مد لغزشی
سیستم تکورودی-تکخروجی (SISO) زیر را در نظر بگیرید:
که در آن، و ، به ترتیب، متغیر خروجی و متغیر ورودی و بردار حالت را نشان میدهند.
هدف کنترل، ردیابی سیگنال خروجی مطلوب است. به عبارت دیگر، بعد از مدت کوتاهی باید خطای به مجاورت بسیار نزدیک صفر میل کند.
همانطور که گفتیم، کنترل مد لغزشی دو بخش دارد و طراحی آن در دو گام زیر انجام میشود:
- مرحله اول: طراحی سطح لغزش
- مرحله دوم: طراحی ورودی کنترل
مرحله اول معادل با تعریف یک تابع اسکالر (نردهای) برحسب حالت سیستم است:
اغلب، سطح لغزش به خطای ردیابی و تعداد مشخصی از مشتقهای آن بستگی دارد:
تابع را باید به گونهای انتخاب کرد که صفر شدن آن () به یک معادله دیفرانسیل «پایدار» منجر شود که در این صورت، هر جواب در نهایت به صفر میل خواهد کرد.
رایجترین انتخاب برای انتخاب «خمینه» (Manifold) لغزش یک ترکیب خطی به صورت زیر است:
تعداد مشتقهای موجود (تعداد ضریب در (۶))، باید برابر با باشد، که در آن، درجه نسبی ورودی-خروجی (۱) و (۲) است.
با انتخاب صحیح ضرایب ، اگر متغیر به صفر میل کند، خطا و مشتقهای آن به صورت نمایی به صفر میل خواهند کرد. اگر چنین شرایطی برقرار باشد، آنگاه وظیفه کنترل صفر کردن در زمان محدود - بدون توجه به هر جنبه دیگری است.
از دیدگاه هندسی، معادله سطحی را در فضای خطا تعریف میکند که «سطح لغزش» نامیده میشود. مسیرهای سیستم تحت کنترل باید به سطح لغزش بروند که در آن، مشخصات طراحی لحاظ شده است.
یک فرم سطح لغزش به صورت زیر است که تنها به پارامتر نردهای بستگی دارد:
انتخاب پارامتر مثبت اغلب دلخواه است و قطب یکتای «دینامیک کاهش یافته» سیستم در حال لغزش را بیان میکند. در طرف مقابل، پارامتر صحیح باید برابر با باشد، که درجه نسبی بین و است. این بدین معنی است که درجه نسبی متغیر برابر با یک است.
گام بعدی (گام دوم) یافتن یک عمل کنترلی است که مسیرهای سیستم را به خمینه لغزش ببرد؛ به عبارت دیگر، کنترل قادر است متغیر را در زمان محدود به صفر میل دهد.
به طور کلی، دو رویکرد بر اساس کنترل مد لغزشی وجود دارد: کنترل مد لغزشی استاندارد (یا مرتبه اول) و کنترل مد لغزشی مرتبه بالا. البته، در برخی منابع، به جای کنترل مد لغزشی مرتبه بالا، کنترل مد لغزشی مرتبه دوم را بیان میکنند. ویژگی مشترک همه روشهای کنترل مد لغزشی این است که در آنها نیازی به اطلاعات دقیق در مورد دینامیک سیستم نیست. به عبارت دیگر، سیستم تحت کنترل به عنوان یک «جعبه سیاه» کاملاً نامعین در نظر گرفته میشود.
کنترل مد لغزشی مرتبه اول
کنترل در خمینه ناپیوسته است:
تابع علامت به گونهای است که:
پارامتر یک ثابت به اندازه کافی بزرگ است.
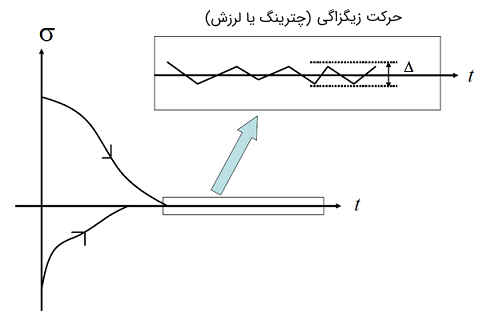 به ازای شرایط اولیه متفاوت" width="483" height="320">
به ازای شرایط اولیه متفاوت" width="483" height="320">در حالات مانا، متغیر کنترل با فرکانس بسیار بالایی (از نظر تئوری، بینهایت) بین مقادیر و نوسان میکند (شکل ۲).
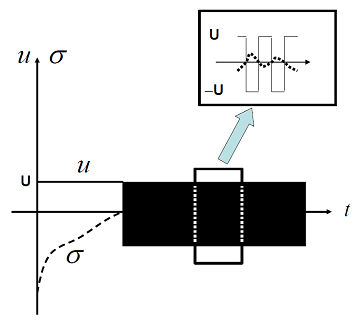 (خطچین را نشان میدهد.)" width="361" height="320">
(خطچین را نشان میدهد.)" width="361" height="320">کنترل سوئیچینگ فرکانس بالای ناپیوسته (شکل ۲) در کاربردهای الکتریکی (که سیگنالهای کنترل PWM به کار میرود) مناسب هستند، اما مثلاً در سیستمهای دینامیکی نوسانات بالا ممکن است منجر به مسائل مختلفی شود.
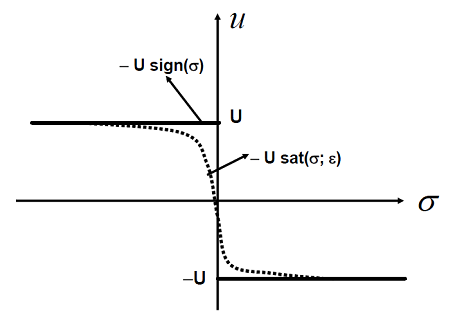
برای حل مشکل مزبور، که به پدیده چترینگ (Chattering Phenomenon) معروف است، از تکنیکهایی، مانند جایگزینی تابع با یک تقریب نَرم پیوسته استفاده میشود. برای مثال، به ترتیب، توابع اشباع (Sat) و تانژانت هیپربولیک (tanh) زیر به کار میروند:
البته این روش در حالتهای خاصی مؤثر عمل میکند. یکی از این موارد وقتی است که نامعینیهای سخت (Hard) وجود نداشته باشند.
کنترل مد لغزشی مرتبه دوم
با استفاده از تقریبهای نرم مرتبه بالا، برخی مسائل به قیمت از دست دادن قوام مرتفع خواهند شد. الگوریتمهای کنترل مد لغزشی مرتبه دوم جایگزینی قوی هستند که پدیده چترینگ را بدون ایجاد مشکل در قوام سیستم حل خواهند کرد.
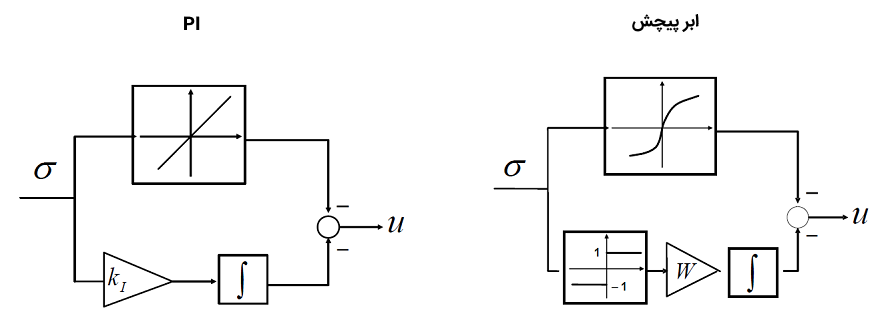
یکی از الگوریتمهای محبوب کنترل مد لغزشی مرتبه دوم، الگوریتم «اَبَرچرخش» (Super Twisting Algorithm) است که در آن، قانون کنترل به صورت زیر در نظر گرفته میشود:
یک راه مناسب برای تنظیم پارامترهای این قانون کنترل، جفت رابطه زیر است:
که در آن، یک ثابت مثبت است که میتوان آن را به اندازه کافی بزرگ انتخاب کرد. در عمل، میتوان را تدریجاً افزایش داد تا عملکرد مناسب سیستم حلقه بسته حاصل شود. این روشِ تکپارامتره «سعی و خطا» در پیادهسازی عملی مفید است و مورد استفاده قرار میگیرد. الگوریتم ابر پیچش را میتوان به عنوان یک نسخه غیرخطی از کنترلکننده PI کلاسیک در نظر گرفت. شکل زیر این موضوع را به خوبی نشان میدهد.
کنترل مد لغزشی مرتبه دوم موضوع چترینگ را حل میکند، زیرا قانون کنترل اکنون یک تابع پیوسته در زمان است. در مثالی که در ادامه ارائه خواهیم کرد، برتری کنترل مد لغزشی مرتبه دوم را در برابر کنترل مد لغزشی استاندارد نشان خواهیم داد.
در حضور دینامیک کنترل نشده، مقداری چترینگ باقی خواهد ماند، اما رویکردهای طراحی خاصی وجود دارند که به مدهای لغزشی مرتبه دوم این قابلیت را میدهند که چنین پدیده نامطلوبی را محدود کند.
مثال طراحی و شبیهسازی
برای بررسی مهمترین جنبه های SMC، مثال کنترل موقعیت یک جرم-فنر-دمپر نامعین را در حضور اغتشاش نامعین متغیر با زمان در نظر میگیریم:
از آنجا که ساختار اغتشاش ناشناخته است، نمیتوان از یک کنترلکننده خطی برای حذف کامل آن استفاده کرد (برخلاف موارد بسیار مشخصی مانند ).
خروجی را به صورت در نظر میگیریم. موقعیت مطلوب برابر است با:
خطای ردیابی را به صورت زیر تعریف میکنیم:
گام اول: طراحی سطح لغزش
درجه نسبی بین خروجی و ورودی برابر با است. بنابراین، بر اساس (۸) (در این مورد )، سطح لغزش را به صورت زیر تعریف میکنیم:
را انتخاب میکنیم و داریم:
گام دوم: طراحی ورودی کنترل
در این مرحله، سه قانون کنترل را پیشنهاد میدهیم:
- کنترل مد لغزشی مرتبه اول:
- کنترل مد لغزشی مرتبه اول نرم شده:
- کنترل مد لغزشی مرتبه دوم ابر پیچشی (Supertwisting 2-SMC):
مقادیر پارامترها ، و هستند.
اغتشاش را نیز به صورت زیر در نظر میگیریم:
نتیجه شبیهسازی SMC مرتبه اول به صورت زیر است.
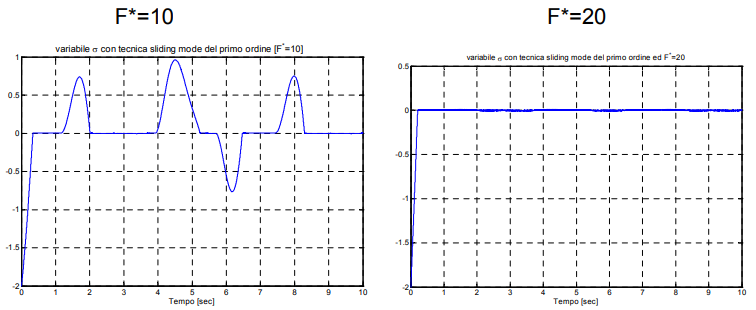 با SMC مرتبه اول" width="756" height="310">
با SMC مرتبه اول" width="756" height="310">در نمودار سمت چپ شکل قدرت کنترل (یعنی پارامتر ) بسیار کم است و در نتیجه، متغیر لغزش از صفر فاصله میگیرد. در نمودار سمت راست، این پارامتر به اندازه کافی افزایش داده شده تا با دقت خوبی در نزدیکی صفر نگه داشته شود.
 . سمت چپ: و . سمت راست: ." width="806" height="276">
. سمت چپ: و . سمت راست: ." width="806" height="276">ورودی کنترل در شکل زیر نشان داده شده است. ماهیت فرکانس بالای ناپیوسته ورودی کنترل در این شکل مشخص است. این رفتار برای یک سیگنال فیزیکی مانند یک نیروی مکانیکی قابل قبول نیست.
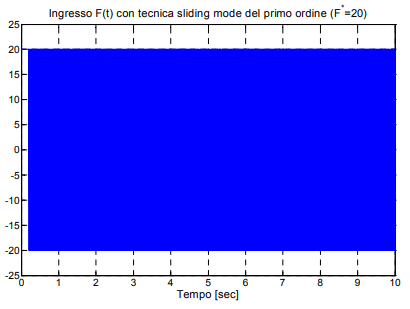 . ورودی کنترل " width="410" height="309">
. ورودی کنترل " width="410" height="309">کنترل مد لغزشی مرتبه اول هموار شده به صورت زیر است:
قانون کنترل بالا ناپیوستگی را از بین میبرد. شکل زیر، نتایج شبیه سازی حاصل از اعمال این قانون کنترل را نشان میدهد.
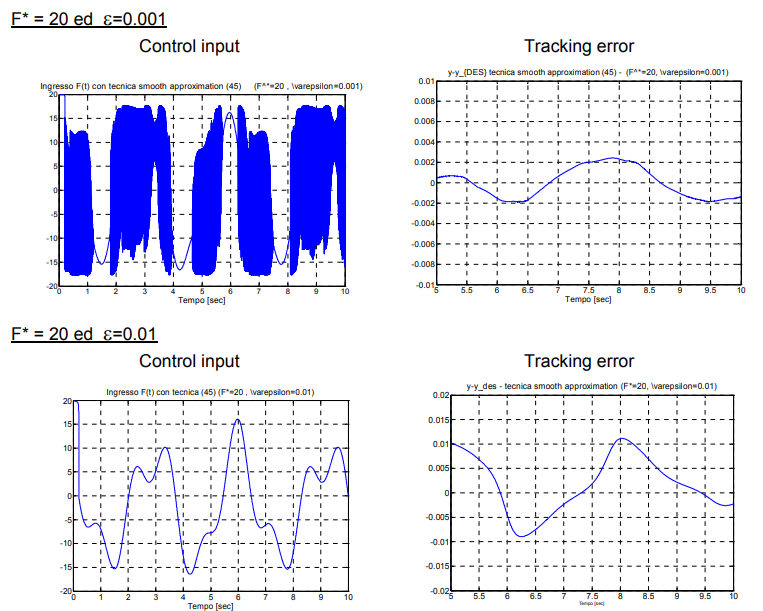
دو شبیهسازی بالا برای کوچک () اثر هموارسازی ورودی کنترل را نشان میدهند، در حالی که دقت کنترل حفظ شده است. برای بزرگتر ()، اثر هموارسازی قابل توجه است، اما دقت کاهش یافته است. بنابراین، باید بین این دو مصالحهای برقرار کنیم.
رویکرد کنترل مد لغزشی مرتبه دوم مشکل چترینگ را حل میکند و در عین حال دقت را بهبود خواهد داد.
شکل زیر، نتیجه شبیهسازی این روش را نشان میدهد. پارامتر تنظیم در نظر گرفته شده است.
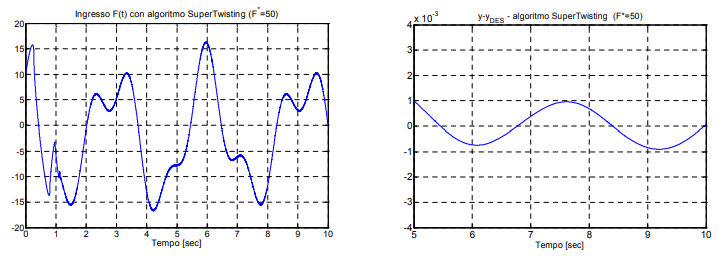 . سمت چپ: ورودی کنترل. سمت راست: خطای ردیابی" width="725" height="256">
. سمت چپ: ورودی کنترل. سمت راست: خطای ردیابی" width="725" height="256">میتوان گفت که دقت بالا و سادگی پیادهسازی این تکنیکها که عملاً بر پایه اطلاعات دینامیک سیستم نیستند به کنترل بسیار دقیق خواهد انجامید.
کاربردهای کنترل مد لغزشی
تاکنون، کنترل مد لغزشی روی سیستمهای مختلفی پیادهسازی شده است. یکی از این کاربردها در مدارهای الکترونیک قدرت و درایوهای الکتریکی است. در این موارد، کنترل مد لغزشی استاندارد با استقبال بسیاری مواجه شده است که از دلایل آن میتوان به ماهیت سوئیچینگ سیگنال کنترل در این سیستمها اشاره کرد که با این نوع کنترلکننده سازگار است. کنترل مد لغزشی مرتبه دوم نیز در موتورهای الکتریکی DC مورد استفاده قرار گرفته است. کنترل سیستمهای قدرت نیز یکی از زمینههای پرکاربرد SMC بوده است. کنترل مد لغزشی مرتبه دوم نیز تاکنون در بسیاری سیستمهای مکانیکی از قبیل جرثقیلها، بازوهای رباتیک و قطارهای مسافربری به کار رفته است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی کنترل
- آموزش طراحی سیستم های کنترل غیرخطی
- مجموعه آموزشهای مهندسی برق
- آموزش سیستم های کنترل غیرخطی با رویکرد حل مساله
- کنترل فازی - از صفر تا صد
- کنترل تطبیقی - از صفر تا صد
- تقلب نامه (Cheat Sheet) کنترل خطی
^^













سلام مرسی. کمتر منبعی داخل نت هست که به این شیوایی توضیح داده باشه. فقط کاش فایل شبیه سازی رو هم قرار میدادین. اگر راجع به شکل 4 هم بیشتر توضیح بدین ممنون میشم.
سلام وقت بخیر ممنون از آموزش خوبتون فقط یک نکته رو میخواستم بگم که در فرمول (1)
g(x,t).u میباشد که به اشتباه g(x,t) نوشته شده.
سلام.
معادله تصحیح شد.
سپاس از همراهی و بازخوردتان.
سلام وقتتون بخیر،از آموزش های خوب و مفیدتون ممنونم.یک سوال درحین آموزش برای من پیش اومد و اون اینکه چرا برای صفر شدن مشتق سطح لغزش در کنترل مد لغزشی به سراغ اثبات پایداری سطح لغزش میرویم؟