معادله گرما — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، درباره معادلات دیفرانسیل با مشتقات جزئی و روش‌های حل آن‌ها بحث کردیم. معادله گرما نمونه‌ای از این معادلات است که در این آموزش به بررسی آن می‌پردازیم.

معادله گرما یا معادله حرارت، توزیع دما را در یک جسم نشان می‌دهد. در مراجع گوناگون، معادلات مختلفی برای گرما تعریف شده است. تمرکز این آموزش بر معادله گرما برای میله یک‌بعدی با طول $$L$$ است. فرض می‌کنیم ابتدای میله در $$x=0$$ و انتهای آن در $$x=L$$ قرار دارد. همچنین فرض می‌کنیم دما سطح مقطع هر موقعیت $$x$$ دلخواه از میله، یکسان و ثابت است. به عبارت دیگر، دمای میله فقط روی محور $$x$$ تغییر می‌کند و می‌توان آن را یک‌بعدی در نظر گرفت. به این ترتیب، شکل سطح مقطع میله (مربع، دایره و...) اهمیت ندارد.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

توجه کنید که فرض یک‌بعدی بودن میله، برخلاف چیزی که در ابتدا به‌نظر می‌رسد، خیلی هم بد نیست، زیرا اگر فرض کنیم سطح جانبی میله کاملاً ایزوله باشد (یعنی امکان جریان گرما روی سطح میله وجود نداشته باشد)، آن‌گاه تنها راه ورود و خروج گرما، ابتدا یا انتهای میله است. این، بدین معنی است که گرما فقط از سمت چپ به راست یا راست به چپ جریان پیدا می‌کند و در نتیجه، توزیع دما یک‌بعدی خواهد بود.

البته، فرض عایق بودن کامل سطح جانبی میله شدنی نیست، اما عایق کردن آن به‌گونه‌ای که مقدار بسیار کمی گرما در آن جریان داشته باشد، امری ممکن است و در نتیجه، حداقل در یک لحظه می‌توان سطح جانی را ایزوله در نظر گرفت.

با توضیحاتی که بیان شد، ابتدا کمیت‌های معادله گرما را معرفی می‌کنیم. عبارت $$u\left( {x,t} \right)$$ دمای نقطه $$x$$ در زمان دلخواه $$t$$ را نشان می‌دهد. همچنین $$c(x)$$ گرمای ویژه، $$\rho (x)$$ جرم مخصوص، $$\varphi (x,t)$$ شار گرمایی و $$Q(x,t)$$ انرژی گرمایی تولیدی در واحد حجم در واحد زمان است.

قبل از بیان معادله گرما، لازم است نکاتی را بیان کنیم. گرمای ویژه $$c\left( x \right) > 0$$ یک ماده،‌ مقدار انرژی گرمایی مورد نیاز برای افزایش یک واحد دما در یک واحد از جرم آن ماده است. همان‌طور که اشاره شد، حداقل در ابتدا فرض می‌کنیم گرمای ویژه میله ممکن است یکنواخت نباشد. در عمل، گرمای ویژه به دما وابسته است. با این حال، این مورد، در اختلاف دماهای زیاد مطرح است (که به نوبه خود بستگی جنس ماده اولیه میله دارد). در این بحث فرض می‌کنیم اختلاف دما به‌اندازه‌ای نیست که روی پاسخ معادله تأثیر بگذارد.

جرم مخصوص $$\rho \left( x \right)$$، جرم بر واحد حجم ماده است. مشابه گرمای ویژه، فرض می‌کنیم در ابتدا جرم مخصوص میله، یکنواخت نباشد.

شار گرمایی $$Q(x,t)$$، مقدار انرژی گرمایی است که در واحد سطح و واحد زمان به سمت راست جریان دارد. عبارت «جریان به سمت راست» به این معنی است که اگر برای $$x$$ و $$t$$ مشخص، $$\varphi \left( {x,t} \right) > 0$$ باشد، گرما، در آن نقطه و زمان به سمت راست جریان دارد. برعکس، اگر $$Q\left( {x,t} \right) < 0$$ باشد،‌ آن‌گاه گرما در جهت چپ آن نقطه عبور خواهد کرد.

آخرین کمیتی که معرفی شد، $$Q\left( {x,t} \right)$$ است که برای نمایش هر منبع خارجی انرژی گرمایی به‌کار می‌رود. اگر $$Q\left( {x,t} \right) > 0$$ باشد، آن‌گاه انرژی گرمایی به سیستم وارد می‌شود و اگر $$Q\left( {x,t} \right) < 0$$، آن‌گاه انرژی گرمایی سیستم از بین می‌رود.

با توجه به کمیت‌هایی که معرفی شد، معادله گرما را به‌صورت زیر تعریف می‌کنیم:

$$\begin{equation}c\left( x \right)\rho \left( x \right)\frac{{\partial u}}{{\partial t}} = - \frac{{\partial \varphi }}{{\partial x}} + Q\left( {x,t} \right)\label{eq:eq1}\end{equation}$$

هرچند معادله فوق، فرم مناسبی از معادله گرما است، اما ظاهراً به‌گونه‌ای نیست که بتوانیم آن را حل کنیم. در این فرم، دو تابع مجهول $$u$$ و $$\varphi$$ وجود دارد و باید به‌طریقی یکی از آن‌ها را حذف کنیم. با استفاده از قانون فوریه، می‌توان به‌سادگی شار گرمایی را از این معادله حذف کرد.

طبق قانون فوریه، داریم:

$$\varphi \left( {x,t} \right) = - {K_0}\left( x \right)\frac{{\partial u}}{{\partial x}}$$

که در آن، $${K_0}\left( x \right) > 0$$ «رسانندگی گرمایی» (Thermal Conductivity) ماده است و توانایی ماده را برای هدایت گرما نشان می‌دهد. ماده‌ای که گرما را بهتر انتقال دهد، $${K_0}\left( x \right)$$ بزرگ‌تری دارد. همان‌گونه که از نماد رسانندگی گرمایی مشخص است، مقدار آن، در طول ($$x$$) لوله متغیر است. همچنین رسانندگی گرمایی، مشابه گرمای ویژه، با دما نیز تغییر می‌کند، اما فرض می‌کنیم تغییر دما بزرگ نباشد. بنابراین، در این‌جا فرض می‌کنیم رسانندگی گرمایی به دما وابسته نیست.

قانون فوریه، نقش مهمی در مدل‌سازی آن‌چه دارد که به‌عنوان شار گرمایی می‌شناسیم. همان‌طور که می‌دانیم، اگر دما در محدوده‌ای ثابت باشد، $$\frac{{\partial u}}{{\partial x}} = 0$$ خواهد بود، در نتیجه شار گرمایی نخواهیم داشت.

همچنین می‌دانیم اگر اختلاف دما در ناحیه‌ای وجود داشته باشد، گرما از بخش گرم به بخش سرد جریان پیدا می‌کند. برای مثال، اگر قسمت گرم‌تر در سمت راست باشد، گرما در جهت چپ جریان خواهد داشت. از سوی دیگر، اگر قسمت گرم‌تر در سمت راست باشد، $$\frac{{\partial u}}{{\partial x}} > 0$$ است (یعنی دما با حرکت به سمت راست افزایش پیدا می‌کند) و در نتیجه $$\varphi < 0$$ است و گرما به سمت چپ جریان خواهد داشت. از طرفی، برای حالتی که سمت چپ میله گرم‌تر است، رابطه $$\frac{{\partial u}}{{\partial x}} < 0$$‌ را داریم که نشان می‌دهد $$\varphi > 0$$ بوده و گرما به سمت راست جریان دارد.

در نهایت، باید گفت که اختلاف دمای بزرگ‌تر در یک ناحیه (یعنی $$\frac{{\partial u}}{{\partial x}}$$ بزرگ‌تر)، به‌معنی شار گرمایی بزرگ‌تر است. اگر قانون فوریه را در معادله گرما جایگذاری کنیم، رابطه زیر را خواهیم داشت:

$$\begin{equation}c\left( x \right)\rho \left( x \right)\frac{{\partial u}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {{K_0}\left( x \right)\frac{{\partial u}}{{\partial x}}} \right) + Q\left( {x,t} \right)\label{eq:eq2}\end{equation}$$

حل معادله اخیر به‌دلیل ماهیت غیریکنواخت ویژگی‌های گرمایی و جرم مخصوص، بسیار دشوار است. بنابراین، فرض می‌کنیم این مشخصات ثابت باشند؛ یعنی:

$$c\left( x \right) = c\hspace{0.25in}\rho \left( x \right) = \rho \hspace{0.25in}{K_0}\left( x \right) = {K_0}$$

که در آن $$c$$، $$\rho$$ و $$K_0$$ مقادیر ثابتی هستند. در این حالت، می‌توان گفت ماده تشکیل‌دهنده میله یکنواخت است. با این فرضیات، معادله گرما را می‌توان به‌صورت زیر نوشت:

 $$\begin{equation}c\rho \frac{{\partial u}}{{\partial t}} = {K_0}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + Q\left( {x,t} \right)\label{eq:eq3}\end{equation}$$

آخرین ساده‌سازی که انجام می‌دهیم، تقسیم دو سمت معادله فوق بر $$c\rho$$ و تعریف «ضریب نفوذ گرمایی» (Thermal Diffusivity) است:

$$k = \frac{{{K_0}}}{{c\rho }}$$

معادله گرما نیز به‌صورت زیر درخواهد آمد:

$$\begin{equation}\frac{{\partial u}}{{\partial t}} = k\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{Q\left( {x,t} \right)}}{{c\rho }}\label{eq:eq4}\end{equation}$$

معادله اخیر را بدون منابع خارجی، یعنی $$Q\left( {x,t} \right) = 0$$ حل می‌کنیم، اما بعد از جداسازی متغیرها این فرم را در دو قسمت بررسی خواهیم کرد. منابع خارجی را فقط موقع حل معادله گرما حذف می‌کنیم.

اکنون که معادله گرما را به‌دست آورده‌ایم، برای حل آن به شرایط اولیه و مرزی نیاز داریم. در آموزش‌های پیشین برای حل معادلات دیفرانسیل دیدیم که تعداد شرایط مورد نیاز برای حل معادله، برابر با بزرگ‌ترین مرتبه مشتق در معادله است.

در معادلات دیفرانسیل جزئی، ایده مشابهی وجود دارد، با این تفاوت که اکنون باید متغیری را در نظر بگیریم که از آن مشتق می‌گیریم. بنابراین، در معادله گرما، مشتق اول وجود دارد و به همین دلیل به یک شرط اولیه نیاز داریم. همچنین، یک مشتق مرتبه دوم داریم و به‌همین دلیل دو شرط مرزی نیز لازم است.

شرط اولیه‌ای که لازم داریم، به‌صورت زیر است:

$$u\left( {x,0} \right) = f\left( x \right)$$

واضح است که شرط اولیه بالا، توزیع دمای اولیه را نشان می‌دهد.

شرایط مرزی، دما و یا شار گرمایی را در مرزهای میله نشان می‌دهد. چهار مورد از این شرایط، معمولاً از بقیه متداول‌تر هستند. اولین دسته از شرایط مرزی، دمای از‌ پیش تعیین شده است که «شرایط دیریکله» (Dirichlet Conditions) نیز نامیده می‌شود. این شرایط مرزی به‌صورت زیر هستند:

$$u\left( {0,t} \right) = {g_1}\left( t \right)\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}u\left( {L,t} \right) = {g_2}\left( t \right)$$

نوع دیگر شرایط مرزی، شار گرمایی از پیش تعیین‌شده است که «شرایط نیومان» (Neumann Conditions) نامیده می‌شود. با استفاده از قانون فوریه، این شرایط را می‌توان به‌صورت زیر نوشت:

$$- {K_0}\left( 0 \right)\frac{{\partial u}}{{\partial x}}\left( {0,t} \right) = {\varphi _1}\left( t \right)\hspace{0.25in}\hspace{0.25in}\hspace{0.25in} - {K_0}\left( L \right)\frac{{\partial u}}{{\partial x}}\left( {L,t} \right) = {\varphi _2}\left( t \right)$$

اگر مرزها کاملاً ایزوله باشند، یعنی شار گرمایی از آن‌ها خارج نشود، شرایط مرزی به‌فرم زیر کاهش می‌یابد:

$$\frac{{\partial u}}{{\partial x}}\left( {0,t} \right) = 0\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\frac{{\partial u}}{{\partial x}}\left( {L,t} \right) = 0$$

شرایط مرزی دسته سوم که گاهی «شرایط مرزی رابین» (Robins Conditions) نامیده می‌شود، از «قانون سرد شدن نیوتن» (Newton’s Law of Cooling) بهره می‌گیرد. از این شرایط وقتی استفاده می‌شود که میله در یک سیال در حال حرکت است. در این حالت می‌توانیم هوا را به‌ عنوان سیال در نظر بگیریم.

روابط مربوط به این شرایط اولیه به‌صورت زیر است:

$$- {K_0}\left( 0 \right)\frac{{\partial u}}{{\partial x}}\left( {0,t} \right) = - H\left[ {u\left( {0,t} \right) - {g_1}\left( t \right)} \right]\hspace{0.25in} - {K_0}\left( L \right)\frac{{\partial u}}{{\partial x}}\left( {L,t} \right) = H\left[ {u\left( {L,t} \right) - {g_2}\left( t \right)} \right]$$

که در آن، $$H$$ یک مقدار مثبت است که به‌صورت تجربی به‌دست می‌آید و $${g_1}\left( t \right)$$ و $${g_2}\left( t \right)$$ دمای سیال را در مرزها نشان می‌دهند.

توجه کنید که ممکن است دو شرط، بسته به اینکه در کدام مرز هستیم، کمی تغییر کنند. در $$x=0$$، یک علامت منفی در سمت راست داریم، در حالی که در $$x=L$$ چنین نیست. برای دانستن دلیل این موضوع، ابتدا فرض کنید $$x = 0$$ باشد، در این حالت، داریم: $$u\left( {0,t} \right) > {g_1}\left( t \right)$$. به عبارت دیگر، میله نسبت به سیال اطرافش گرم‌تر است و بنابراین در $$x=0$$ جهت شار گرمایی (که در سمت چپ معادله داده شده است) باید به سمت چپ یا منفی باشد، زیرا گرما از میله گرم به سیال اطراف جریان پیدا می‌کند. اگر شار گرمایی منفی باشد، آن‌گاه باید یک علامت منفی در سمت راست معادله قرار دهیم تا مطمئن شویم علامت آن مناسب است.

اگر میله در $$x=0$$ سردتر از سیال محیط باشد، یعنی $$u\left( {0,t} \right) < {g_1}\left( t \right)$$، می‌توان موارد مشابهی را برای توجیه علامت منفی بیان کرد. برای $$x=L$$‌، دوباره فرض می‌کنیم میله گرم‌تر از سیال است یا به عبارت دیگر $$u\left( {L,t} \right) > {g_2}\left( t \right)$$. در این حالت، شار گرمایی باید به سمت راست در جریان باشد یا به‌عبارتی مثبت باشد. بنابراین، در این حالت، علامت منفی وجود ندارد.

جالب است بدانید که می‌توان شرایط مرزی مختلف را با هم ترکیب کرد. مثلاً می‌توان دمای از پیش تعیین شده را در یک مرز و شار گرمایی از پیش تعیین شده را در مرز دیگر در نظر گرفت. بنابراین ممکن است نوع شرایط مرزی دو مرز با هم فرق داشته باشد.

نوع آخر شرایط مرزی، شرایط مرزی تناوبی یا متناوب است. شرایط مرزی متناوب به‌صورت زیر هستند:

$$u\left( { - L,t} \right) = u\left( {L,t} \right)\hspace{0.25in}\hspace{0.25in}\frac{{\partial u}}{{\partial x}}\left( { - L,t} \right) = \frac{{\partial u}}{{\partial x}}\left( {L,t} \right)$$

برای شرایط مرزی فوق، به‌جای آنکه مرز چپ را $$x=0$$ در نظر بگیریم، آن را برابر با $$x=-L$$ فرض می‌کنیم. شرایط مرزی متناوب، به‌صورت طبیعی از یک جفت هندسه خاص به‌دست خواهد آمد که در ادامه، آن را خواهیم دید.

در ادامه، معادلات گرمای دوبعدی و سه‌بعدی را به‌صورت کاملاً اجمالی بررسی خواهیم کرد. البته قبل از آن لازم است با چند نمادگذاری آشنا شویم.

عملگر دِل (Del) دوبعدی و سه بعدی را به‌ترتیب، به‌صورت زیر تعریف می‌کنیم:

$$\nabla = \frac{\partial }{{\partial x}}\vec i + \frac{\partial }{{\partial y}}\vec j\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\nabla = \frac{\partial }{{\partial x}}\vec i + \frac{\partial }{{\partial y}}\vec j + \frac{\partial }{{\partial k}}\vec k$$

عملگر دل را می‌توان به‌عنوان یک تابع در نظر گرفت که توابع (به‌جای اعداد)، آرگومان‌های آن هستند. اگر اپراتور دل را بر تابعی اعمال کنیم، در حقیقت نسبت به آن تابع، مشتق جزئی می‌گیریم.

فیلم آموزش انتقال حرارت – حل تست های کنکور ارشد و دکتری در فرادرس

کلیک کنید

برای مثال، در حالت سه‌بعدی داریم:

$$\nabla f = \frac{{\partial f}}{{\partial x}}\vec i + \frac{{\partial f}}{{\partial y}}\vec j + \frac{{\partial f}}{{\partial k}}\vec k$$

عبارت بالا، گرادیان تابع $$f\left( {x,y,z} \right)$$ است.

با استفاده از اپراتور دل، همچنین می‌توان به‌سرعت دیورژانس یک تابع را محاسبه کرد. باز هم در فضای سه‌بعدی می‌توان دیورژانس تابع $$f\left( {x,y,z} \right)$$ را به‌صورت ضرب نقطه‌ای عملگر دل و تابع نوشت:

$$\nabla \small \bullet f = \frac{{\partial f}}{{\partial x}} + \frac{{\partial f}}{{\partial y}} + \frac{{\partial f}}{{\partial k}}$$

برای استفاده در معادله گرما، می‌توان عبارت زیر را نوشت:

$$\nabla \small \bullet \left( {\nabla f} \right) = \frac{\partial }{{\partial x}}\left( {\frac{{\partial f}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{\partial f}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\partial f}}{{\partial k}}} \right) = \frac{{{\partial ^2}f}}{{\partial {x^2}}} + \frac{{{\partial ^2}f}}{{\partial {y^2}}} + \frac{{{\partial ^2}f}}{{\partial {z^2}}}$$

عبارت بالا را می‌توان به‌صورت زیر بیان کرد:

$${\nabla ^2}f = \frac{{{\partial ^2}f}}{{\partial {x^2}}} + \frac{{{\partial ^2}f}}{{\partial {y^2}}} + \frac{{{\partial ^2}f}}{{\partial {z^2}}}$$

که به‌عنوان لاپلاسین شناخته می‌شود. واضح است که اگر عبارت فوق را برای حالت دوبعدی بنویسیم، جمله سوم حذف خواهد شد.

اکنون می‌توانیم معادله گرمای دوبعدی و سه‌بعدی را تعریف کنیم که در آن‌ها از اپراتور دل یا لاپلاسین استفاده می‌شود.

معادله اول را به‌خاطر بیاورید که برای بیان گرما معرفی کردیم:

$$\begin{equation}c\left( x \right)\rho \left( x \right)\frac{{\partial u}}{{\partial t}} = - \frac{{\partial \varphi }}{{\partial x}} + Q\left( {x,t} \right)\end{equation}$$

نسخه با ابعاد بزرگ‌تر این معادله به‌صورت زیر است:

$$\begin{equation}c\rho \frac{{\partial u}}{{\partial t}} = - \nabla \small \bullet \,\varphi + Q\label{eq:eq5}\end{equation}$$

در معادله بالا، $$c$$ گرمای ویژه و $$\rho$$ جرم مخصوص هستند که ممکن است یکنواخت نباشند. بنابراین، ممکن است توابعی از متغیرهای فضایی باشند. به همین ترتیب، جمله منبع خارجی $$Q$$ ممکن است تابعی از متغیرهای فضایی و زمان باشد.

نسخه با ابعاد بزرگ‌تر قانون فوریه به‌صورت زیر است:

$$\varphi = - {K_0}\nabla u$$

که در آن، رسانندگی گرمایی $$K_0$$ نیز به‌عنوان تابعی از متغیرهای فضایی فرض می‌شود:

$$c\rho \frac{{\partial u}}{{\partial t}} = \nabla \small \bullet \,\left( {{K_0}\nabla u} \right) + Q$$

اکنون اگر فرض کنیم گرمای ویژه، جرم مخصوص و رسانندگی گرمایی ثابت باشد (یعنی میله یکنواخت باشد)، معادله گرما، به‌صورت زیر درخواهد آمد:

 $$\begin{equation}\frac{{\partial u}}{{\partial t}} = k{\nabla ^2}u + \frac{Q}{{cp}}\label{eq:eq6}\end{equation}$$

که هر دو سمت آن را برای به‌دست آوردن ضریب نفوذ گرمایی $$k$$، بر $$c\rho$$ تقسیم کرده‌ایم.

شرط اولیه معادله گرمای دوبعدی و سه‌بعدی به‌صورت زیر است:

$$u\left( {x,y,t} \right) = f\left( {x,y} \right)\hspace{0.25in}\hspace{0.25in}$$ یا  $$\hspace{0.25in}\hspace{0.25in}u\left( {x,y,z,t} \right) = f\left( {x,y,z} \right)$$

بنابراین، شرط مرزی دمای از پیش‌ تعیین‌ شده به‌صورت زیر خواهد بود:

$$u\left( {x,y,t} \right) = T\left( {x,y,t} \right)\hspace{0.25in}\hspace{0.25in}$$ یا $$\hspace{0.25in}\hspace{0.25in}u\left( {x,y,z,t} \right) = T\left( {x,y,z,t} \right)$$

که $$\left( {x,y} \right)$$ یا $$\left( {x,y,z} \right)$$ به ابعاد بستگی دارد.

شرط شار گرمایی از پیش تعیین شده نیز به‌‌شکل زیر است:

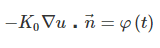
که در آن، سمت در نقاط مرزی تعیین می‌شود و $$\vec n$$ واحد نرمال بر سطح است.

قانون سرد کردن نیوتن نیز به‌صورت زیر خواهد بود:

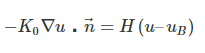
که در آن $$H$$ یک کمیت ثابت است و به‌صورت تجربی محاسبه می‌شود. $$u_B$$ نیز دمای سیال در مرزها است و آن را مانند قبل در نظر می‌گیریم.

در حالت دوبعدی و سه‌بعدی، شرایط مرزی متناوب نداریم، زیرا فقط از هندسه‌های یک‌بعدی خاص به‌وجود می‌آید.

باید اذعان کرد که حل معادله گرمای زیر در هر نقطه امکان‌پذیر نیست:

$$\begin{equation}\frac{{\partial u}}{{\partial t}} = k{\nabla ^2}u + \frac{Q}{{cp}}\end{equation}$$

اما حالت خاصی از آن را می‌توان با معادله لاپلاس حل کرد.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• معادله دیفرانسیل برنولی — از صفر تا صد
• ﻣﻌﺎدﻻت دﯾﻔﺮاﻧﺴﯿﻞ ﺑﺎ ﻣﺸﺘﻘﺎت ﺟﺰﺋﯽ — از صفر تا صد
• دستگاه معادلات دیفرانسیل خطی — به زبان ساده
• معادلات دیفرانسیل مرتبه اول — روش‌های حل به زبان ساده

^^