قضیه حد مرکزی و تعمیم آن — به زبان ساده

یکی از قضیه‌های مهم و البته کاربردی در نظریه آمار، «قضیه حد مرکزی» (Central Limit Theorem) است که گاهی آن را به صورت CLT نیز نشان می‌دهند. به کمک این قضیه ارتباط بین متغیرهای تصادفی با توزیع‌های مختلف با «توزیع نرمال» (Normal Distribution) یا «توزیع گاوسی» (Gaussian Distribution) بیان می‌شود. در این نوشتار به بررسی قضیه حد مرکزی و تعمیم آن خواهیم پرداخت و شرایط استفاده از آن را مرور خواهیم کرد. همچنین نگاهی هم به «قضیه حد مرکزی تعمیم یافته» (Generalized Central Limit Theorem) خواهیم داشت که مرتبط با «توزیع‌های پایدار» (Stable Distributions) است. علاوه بر این موارد این قضیه را در حالت چند متغیره نیز مورد کاوش قرار خواهیم داد.

برای آشنایی بیشتر با توزیع نرمال بهتر است مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را مطالعه کنید. گاهی در این متن به قانون اعداد بزرگ اشاره خواهیم کرد. بنابراین بهتر است مطلب امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را نیز مطالعه کرده باشید. از طرفی آگاهی از خصوصیات توزیع‌های پایدار که در نوشتار خانواده توزیع های پایدار — مفاهیم اولیه به آن پرداخته‌ایم، خالی از لطف نیست.

قضیه حد مرکزی و تعمیم آن

قضیه حد مرکزی مرتبط با توزیع مجموع متغیرهای تصادفی مستقل و هم توزیع است. به این ترتیب اگر بدانیم که $$X_1,X_2,\cdots,X_n$$ متغیرهای مستقلی هستند و البته توزیع یکسانی هم دارند (در این حالت به آن‌ها iid می‌گوییم) می‌توانیم توزیع احتمال مجموع آن‌ها را، زمانی که $$n$$ به اندازه کافی بزرگ باشد، نرمال در نظر بگیریم. نکته جالب در این قضیه عدم اطلاع از توزیع متغیرهای تصادفی است.

فیلم آموزش آمار ریاضی 2 – آزمون فرض در فرادرس

کلیک کنید

شرط متناهی بودن واریانس، مستقل و هم توزیع بودن متغیرهای تصادفی $$X$$ از پیش‌نیازهای اصلی استفاده از این قضیه است. به این ترتیب شرایط استفاده از قضیه حد مرکزی را به صورت زیر معرفی می‌کنیم.

• متغیرهای تصادفی دارای توزیع یکسان باشند. به این معنی که علاوه بر هم خانواده بودن توزیع متغیرها باید پارامترهای یکسانی داشته باشند. البته ممکن است این پارامتر‌ها از قبل مشخص نباشند.
• متغیرهای تصادفی باید از یکدیگر مستقل باشند. از آنجایی که اثبات این قضیه بوسیله تابع مشخصه انجام می‌شود، باید بتوان توزیع توام متغیرها را به صورت حاصلضرب توزیع‌ها نوشت. از آنجایی که این کار در صورت استقلال متغیرها امکان‌پذیر است، یکی از شرایط مهم در قضیه حد مرکزی مستقل بودن متغیرهای تصادفی در نظر گرفته شده است.
• متناهی بودن واریانس نیز از شرایط دیگر و مهم برای قضیه حد مرکزی است. اگر واریانس متغیرهای تصادفی ثابت و متناهی نباشند، قضیه حد مرکزی اعتبار خود را از دست خواهد داد و ممکن است مجموع دنباله‌ای از متغیرهای تصادفی به یک توزیع پایدار دیگر میل کند.

برای محاسبه احتمال بسیاری از توزیع‌ها، می‌توان از تقریب نرمال استفاده کرد. برای مثال می‌توان به پرتاب یک سکه اشاره کرد. اگر متغیر تصادفی $$X$$ را برابر با مقدار ۱ در صورت مشاهده شیر و مقدار صفر در صورت خط بودن سکه در نظر بگیریم، واضح است که با یک «توزیع برنولی» (Bernoulli Distribution) مواجه هستیم. به منظور برآورد احتمال موفقیت (احتمال مشاهده شیر) سکه را به تعداد زیاد پرتاب می‌کنیم.

از آنجایی که هر بار پرتاب سکه مستقل از دفعات دیگر است و پارامتر توزیع برنولی در هر بار تکرار تغییر نمی‌کند (توزیع برنولی با پارامتر ثابت)، مشخص است که مجموع این متغیرهای تصادفی برنولی، دارای «توزیع دوجمله‌ای» (Binomial Distribution) است. با توجه به بزرگ بودن مقدار $$n$$ (تکرار آزمایش‌های پرتاب سکه) محاسبه احتمال براساس توزیع دوجمله‌ای سخت خواهد بود. قضیه حد مرکزی از آنجایی که واریانس توزیع برنولی متناهی است قابل استفاده بوده و می‌توان توزیع احتمالی برای مجموع یا میانگین $$X$$ها که به نوعی برآورد برای احتمال موفقیت در آزمایش برنولی است را توزیع نرمال در نظر گرفت. البته شرط مستقل و هم توزیع‌ بودن به همراه ثابت بودن واریانس در این مثال مشخص است.

قضیه حد مرکزی کلاسیک

شکل‌ها و شرایط مختلفی برای قضیه حد مرکزی وجود دارد. در این قسمت به بررسی قضیه حد مرکزی کلاسیک می‌پردازیم. صورت این قضیه به تفسیر زیر است.

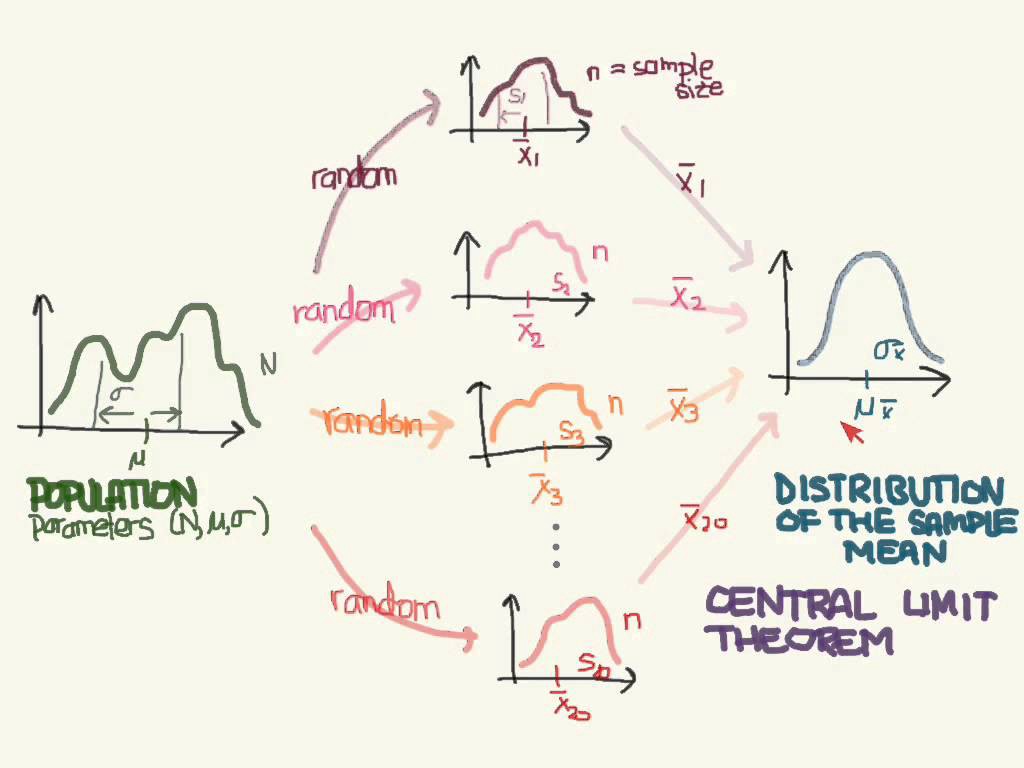
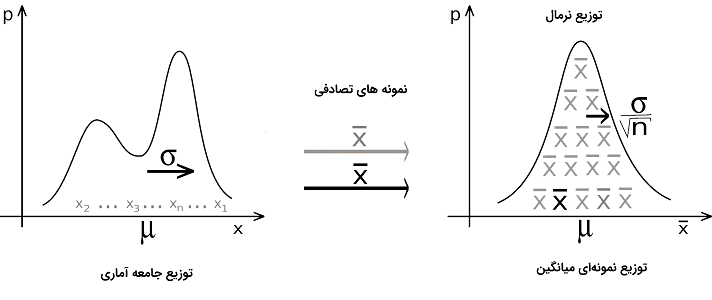
قضیه حد مرکزی: فرض کنید، یک نمونه تصادفی $$n$$تایی مستقل و هم‌توزیع (iid) به صورت $$X_1,X_2,\cdots,X_n$$ در اختیار داریم. امید ریاضی توزیع $$X$$ها برابر با $$\mu$$ و واریانس آن‌ها نیز $$\sigma^2$$ است. در این صورت میانگین نمونه‌ای یا $$S_n$$ که به صورت زیر معرفی می‌شود به طور مجانبی (با افزایش $$n$$) دارای توزیع نرمال خواهد بود که گاهی آن را توزیع نمونه‌ای میانگین می‌گویند.

$$\large S_n=\dfrac{(X_1+X_2+\cdots,X_n)}{n}$$

البته طبق شرایط مطرح شده و «قانون اعداد بزرگ» (Law of Large Numbers) می‌دانیم که میانگین نمونه‌ای به میانگین توزیع میل خواهد کرد. یعنی رابطه زیر برقرار است.

$$\large \lim_{n\rightarrow \infty}S_n =\mu$$

ولی قضیه حد مرکزی از این مرحله یک گام به جلو برداشته و در مورد توزیع $$S_n$$ نیز توضیح می‌دهد. در این صورت می‌توان رابطه زیر را طبق قضیه حد مرکزی نوشت.

$$\large {\displaystyle {\sqrt {n}}\left(S_{n}-\mu \right)\ {\xrightarrow {d}}\ N\left(0,\sigma ^{2}\right)}$$

رابطه بالا می‌تواند به شکل تقریبی و مجانبی، تابع احتمال میانگین توزیع یعنی $$S_n$$‌ را مشخص کند. به این ترتیب رابطه زیر نیز برقرار خواهد بود.

$$\large {\displaystyle S_{n}\xrightarrow {d}} N\left(\mu,\dfrac{\sigma ^{2}}{n}\right)$$

قضیه حد مرکزی لیندبرگ-لوی

فرض کنید دنباله‌ای از متغیرهای تصادفی مستقل و هم‌توزیع (iid) به صورت $$\{X_1, X_2, \cdots\}$$ موجود باشد که $$E[X_i]=\mu ,\;\; Var[X_i]=\sigma^2<\infty$$. اگر $$n$$ به اندازه کافی بزرگ باشد ($$n\rightarrow\infty$$) آنگاه رابطه زیر برقرار است.

$$\large {\displaystyle {\sqrt {n}}\left(S_{n}-\mu \right)\ {\xrightarrow {d}}\ N\left(0,\sigma ^{2}\right)}$$

با توجه به اینکه همگرایی در توزیع موضوع مورد بحث در قضیه حد مرکزی است، می‌توان همگرایی نقطه به نقطه (Pointwise) برای تابع توزیع را نیز در نظر گرفت. به این ترتیب برای پیدا کردن احتمال تقریبی تا نقطه $$z$$ برای مجموع یا میانگین متغیرهایی تصادفی با هر توزیعی، از قضیه حد مرکزی استفاده می‌شود. در این صورت رابطه زیر برقرار خواهد بود. واضح است که منظور از $$\Phi(\frac{z}{\sigma})$$ تابع توزیع متغیر تصادفی نرمال استاندارد است.

$$\large {\displaystyle \lim _{n\to \infty }\Pr \left[{\sqrt {n}}(S_{n}-\mu )\leq z\right]=\Phi \left({\frac {z}{\sigma }}\right)}$$

نکته: تفاوت این قضیه با حالت کلاسیک در دنباله نامتناهی از متغیرهای تصادفی است.

قضیه حد مرکزی در حالت چند بُعدی

اگر فرض کنیم که دنباله‌ای از متغیرهای تصادفی $$p$$ بُعدی داشته باشیم که دارای بردار میانگین $$\mu$$ و ماتریس کوواریانس $$\Sigma_{p\times p}$$ باشند، بطوری که $$X_i$$ها از یکدیگر مستقل و هم‌توزیع هستند، قضیه حد مرکزی را در حالت چند بُعدی نیز می‌توان مطرح کرد. به این ترتیب می‌توان گفت که مجموع بردارهای تصادفی $$X_i$$ با افزایش $$n$$ دارای توزیع نرمال چند متغیره خواهد بود. این موضوع به بیان ریاضی به صورت زیر نوشته می‌شود.

فیلم آموزش تجزیه و تحلیل آماری با نرم افزار StatPlus در فرادرس

کلیک کنید

فرض کنید بردار تصادفی $$n$$‌ تایی به صورت زیر داشته باشیم. این متغیرها $$p$$ بُعدی در نظر گرفته شده‌اند.

$$\large {\displaystyle \mathbf {X} _{i}={\begin{bmatrix}X_{i(1)}\\\vdots \\X_{i(p)}\end{bmatrix}}}; i=1,2,\cdots,n$$

در این حالت مجموع این بردارهای تصادفی به شکل زیر در خواهد آمد.

$$\large {\displaystyle {\begin{bmatrix}X_{1(1)}\\\vdots \\X_{1(p)}\end{bmatrix}}+{\begin{bmatrix}X_{2(1)}\\\vdots \\X_{2(p)}\end{bmatrix}}+\cdots +{\begin{bmatrix}X_{n(1)}\\\vdots \\X_{n(p)}\end{bmatrix}}={\begin{bmatrix}\sum _{i=1}^{n}\left[X_{i(1)}\right]\\\vdots \\\sum _{i=1}^{n}\left[X_{i(p)}\right]\end{bmatrix}}=\sum _{i=1}^{n}\mathbf {X} _{i}}$$

به این ترتیب میانگین این بردارهای تصادفی براساس مجموعشان بدست خواهد آمد.

$$\large {\displaystyle {\frac {1}{n}}\sum _{i=1}^{n}\mathbf {X} _{i}={\frac {1}{n}}{\begin{bmatrix}\sum _{i=1}^{n}X_{i(1)}\\\vdots \\\sum _{i=1}^{n}X_{i(k)}\end{bmatrix}}={\begin{bmatrix}{\bar {X}}_{i(1)}\\\vdots \\{\bar {X}}_{i(k)}\end{bmatrix}}=\mathbf {{\bar {X}}_{n}} }$$

در نتیجه رابطه زیر برقرار است.

$$\large{\displaystyle {\frac {1}{\sqrt {n}}}\sum _{i=1}^{n}\left[\mathbf {X} _{i}-\operatorname {E} \left(X_{i}\right)\right]={\frac {1}{\sqrt {n}}}\sum _{i=1}^{n}(\mathbf {X} _{i}-{\boldsymbol {\mu }})={\sqrt {n}}\left({\overline {\mathbf {X} }}_{n}-{\boldsymbol {\mu }}\right)}$$

طبق قضیه حد مرکزی خواهیم داشت:

$$\large{\displaystyle {\sqrt {n}}\left({\overline {\mathbf {X} }}_{n}-{\boldsymbol {\mu }}\right)\ {\stackrel {D}{\rightarrow }}\ N_{p}(0,{\boldsymbol {\Sigma }})}$$

بطوری که ماتریس کوواریانس $$\Sigma$$ مطابق با رابطه زیر محاسبه می‌شود.

$$\large{\displaystyle {\boldsymbol {\Sigma }}={\begin{bmatrix}{\operatorname {Var} \left(X_{1(1)}\right)}&\operatorname {Cov} \left(X_{1(1)},X_{1(2)}\right)&\operatorname {Cov} \left(X_{1(1)},X_{1(3)}\right)&\cdots &\operatorname {Cov} \left(X_{1(1)},X_{1(k)}\right)\\\operatorname {Cov} \left(X_{1(2)},X_{1(1)}\right)&\operatorname {Var} \left(X_{1(2)}\right)&\operatorname {Cov} \left(X_{1(2)},X_{1(3)}\right)&\cdots &\operatorname {Cov} \left(X_{1(2)},X_{1(k)}\right)\\\operatorname {Cov} \left(X_{1(3)},X_{1(1)}\right)&\operatorname {Cov} \left(X_{1(3)},X_{1(2)}\right)&\operatorname {Var} \left(X_{1(3)}\right)&\cdots &\operatorname {Cov} \left(X_{1(3)},X_{1(k)}\right)\\\vdots &\vdots &\vdots &\ddots &\vdots \\\operatorname {Cov} \left(X_{1(k)},X_{1(1)}\right)&\operatorname {Cov} \left(X_{1(k)},X_{1(2)}\right)&\operatorname {Cov} \left(X_{1(k)},X_{1(3)}\right)&\cdots &\operatorname {Var} \left(X_{1(k)}\right)\\\end{bmatrix}}}$$

نکته: توجه داشته باشید که این ماتریس، ارتباط بین متغیرهای تصادفی نیست زیرا فرض بر این است که متغیرها از یکدیگر مستقل هستند. پس مشخص است که ماتریس کوواریانس مربوط به میزان ارتباط بین ابعاد متغیرها است نه خود متغیرها.

تعمیم قضیه حد مرکزی

«توزیع‌های پایدار» (Stable Distributions) در تعمیم قضیه حد مرکزی کاربرد دارند. تعمیم قضیه حد مرکزی توسط «بوریس گندنکو» (Boris Gnedenko) و «آندری کولموگروف» (Andry Kolmogrov) در سال 1954 مطرح و اثبات شد.

این قضیه نشان می‌دهد که مجموع متغیرهای تصادفی با توزیع متقارن و با واریانس نامتناهی که دارای «توزیع دم سنگین» (Heavy Tailed Distribution) هستند (تغییرات در دم‌های توزیع برای $$\alpha<2$$ و نامنفی به صورت $$|x|^{-\alpha-1}$$ باشد) با افزایش $$n$$ به سمت توزیع پایدار $$f(x;\alpha,0,c,0)$$ میل خواهد کرد. اگر $$\alpha>2$$ باشد، واریانس متناهی بوده و می‌توان مطابق با قضیه حد مرکزی، توزیع حدی میانگین یا مجموع متغیرهای تصادفی iid را نرمال فرض کرد.

نکته: $$\alpha$$ را پارامتر پایداری، $$c$$ را هم پارامتر مقیاس می‌نامند. توضیحات بیشتر در مورد پارامترهای توزیع پایدار را در نوشتار توزیع های پایدار — مفاهیم اولیه  مطالعه کنید.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
• متغیر تصادفی و توزیع کوشی (Cauchy Distribution) — به زبان ساده
• توزیع های آماری F و T — مفاهیم و کاربردها

^^