اکسترمم مطلق و محاسبه آن — به زبان ساده (+ فیلم آموزش گام به گام)

در مطالب قبلی وبلاگ فرادرس با مفهوم ماکزیمم و مینیمم آشنا شدیم و شیوه به دست آوردن اکسترمم و نقاط بحرانی با استفاده از تعریف مشتق و مشتق جزئی مورد مطالعه قرار گرفت. در این مطلب به صورت دقیق به بررسی مفهوم اکسترمم مطلق و شیوه محاسبه آن پرداخته می‌شود.

بنابراین تابع پیوسته $$f \left ( x \right )$$ را در بازه $${ \left [ { a , b } \right ] }$$ در نظر بگیرید. هدف ما در این مطلب، محاسبه مقدار اکسترمم مطلق این تابع در بازه مورد نظر است. بر این اساس، برای محاسبه مقدار اکسترمم مطلق، از مفاهیم و روابطی که در سایر مطالب وبلاگ فرادرس بیان شد نیز استفاده می‌شود.

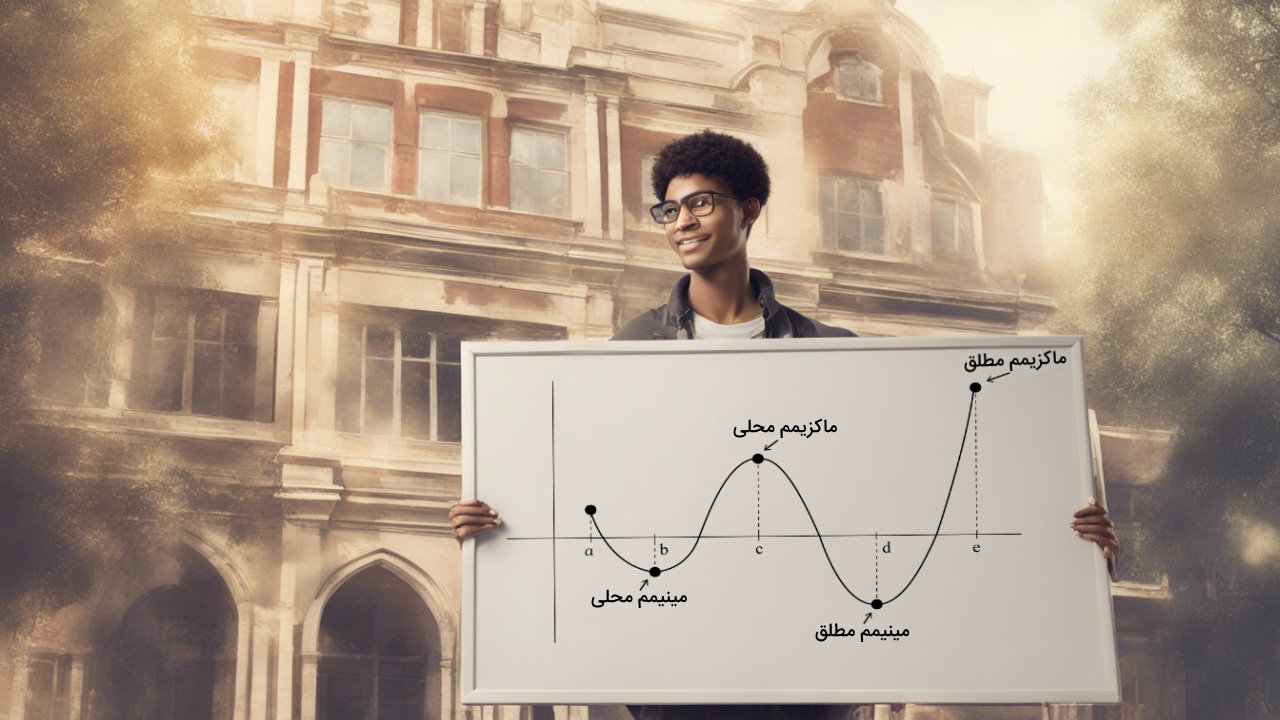
اکسترمم مطلق تابع

توجه کنید که اکسترمم مطلق یک تابع در یک بازه معین، ماکزیمم یا مینیمم مقدار این تابع در بازه تعیین شده را نشان می‌دهد. بنابراین اکسترمم مطلق می‌تواند نقاط یکی از نقاط اکسترمم نسبی باشد و یا نقاط ابتدا و انتهای بازه را در بر بگیرد.

مطابق توضیحات بیان شده، ابتدا باید لیستی از نقاطی را تعیین کنیم که احتمالا اکسترمم مطلق تابع مورد نظر در بازه تعیین شده هستند و در ادامه مقدار تابع در نقاط مختلف این لیست را تعیین و با یکدیگر مقایسه کنیم. در نهایت مقدار ماکزیمم یا مینیمم تابع در این بازه را به عنوان اکسترمم مطلق در نظر می‌گیریم. روند تعیین اکسترمم مطلق یک تابع را در ادامه به صورت مرحله به مرحله و دقیق مورد بررسی قرار می‌دهیم.

مراحل محاسبه اکسترمم مطلق تابع

در قسمت قبل، مراحل مختلف محاسبه اکسترمم مطلق به صورت کلی بیان شد، اما در این قسمت به صورت جزئی‌تر به بیان این روند پرداخته می‌شود.

مرحله اول: تابع پیوسته

در ابتدا با انجام محاسبات مختلف، مطمئن شوید که تابع مورد نظر در بازه تعیین شده پیوسته است.

مرحله دوم: محاسبه نقاط بحرانی

در مرحله دوم، تمام نقاط بحرانی تابع $${ f \left ( x \right ) }$$ را در بازه $${ \left [ { a , b } \right ] }$$ به دست آوردید. بنابراین با استفاده از این کار، شما تمام نقاط ماکزیمم و مینیمم نسبی تابع در بازه مورد نظر را به دست آورده‌اید. نکته مهمی که باید به آن توجه کنید این است که از آنجایی که ما به دنبال یافتن نقاط اکسترمم مطلق تابع در بازه $${ \left [ { a , b } \right ] }$$ هستیم، نقاط بحرانی خارج از این بازه برای ما اهمیت ندارند.

مرحله سوم: محاسبه مقدار تابع در نقاط بحرانی، ابتدا و انتها

در این مرحله، مقدار تابع را در نقاط بحرانی که در مرحله قبل به دست آمدند را محاسبه می‌کنیم. همچنین مقدار این تابع در نقاط ابتدا و انتهایی بازه را نیز مورد محاسبه قرار می‌دهیم.

مرحله چهارم: تعیین اکسترمم مطلق

در این مرحله، مقادیر محاسبه شده در مرحله سوم را با یکدیگر مقایسه می‌کنیم و کوچکترین مقدار را به عنوان مینیمم مطلق و بزرگترین مقدار را به عنوان ماکزیمم مطلق در نظر می‌گیریم. این دو مقدار، اکسترمم مطلق تابع $${ f \left ( x \right ) }$$ را در بازه $${ \left [ { a , b } \right ] }$$ هستند.

بنابراین مراحل مختلف محاسبه اکسترمم مطلق به صورت دقیق شرح داده شد. در ادامه و به کمک چند مثال، شیوه استفاده از این مراحل مورد بررسی قرار گرفته است.

مثال 1

اکسترمم مطلق تابع زیر را در بازه $${ \left [ { - { 4 } , 2 } \right ] }$$ مورد محاسبه قرار دهید.

$${ \large { g } \left ( { t } \right ) = { 2 } { { t } ^ { 3 } } + { 3 } { { t } ^ { 2 } } - 1 2 { t } + 4 }$$

برای به دست آوردن مقدار اکسترمم مطلق این تابع، مراحل چهارگانه توضیح داده شده در درسنامه را پیگیری می‌کنیم. بنابراین ابتدا توجه کنید که این تابع یک چند جمله‌ای است، بنابراین در تمام نقاط بازه مورد نظر، به صورت پیوسته خواهد بود.

در مرحله دوم به محاسبه نقاط بحرانی این تابع می‌پردازیم. همانطور که می‌دانیم، نقاط بحرانی شامل نقاطی در دامنه تابع هستند که در آن‌ها مشتق تابع برابر با صفر است و یا مشتق در این نقاط وجود ندارد. بنابراین برای محاسبه نقاط بحرانی این تابع، ابتدا از تابع مورد نظر مشتق می‌‌گیریم. این موضوع در رابطه زیر به خوبی نشان داده شده است.

$${ \large { g } ^ \prime \left ( { t } \right ) = { 6 } { { t } ^ { 2 } } + 6 { t } - 1 2 = 6 \left ( { { t } + 2 } \right ) \left ( { { t } - 1 } \right ) }$$

برای آشنایی با نحوه تجزیه یک عبارت دو جمله‌ای که در رابطه بالا انجام شده است، به مبحث «اتحاد و تجزیه در ریاضی» در وبلاگ فرادرس مراجعه کنید. در ادامه برای محاسبه نقاط بحرانی تابع، مشتق محاسبه شده در رابطه بالا را برابر با صفر قرار می‌دهیم. بنابراین دو نقطه زیر، نقاط بحرانی این تابع در نظر گرفته می‌شوند.

$${ \large t = - 2 }$$

$${ \large t = 1 }$$

این دو نقطه، در دامنه تابع و در بازه تعیین شده در صورت سوال قرار دارند. بنابراین این دو نقطه، نقاط قابل قبولی برای ما محسوب می‌شوند. در ادامه به بررسی مرحله سوم پرداخته می‌شود. بر این اساس، مقدار تابع را در نقاط ابتدا و انتها و همچنین نقاط بحرانی مورد محاسبه قرار می‌هیم. این موضوع در رابطه زیر به خوبی نشان داده شده است.

$${ \large \begin {align*} { g } \left ( { - { 2 } } \right ) & = 2 4 \hspace { 1.0 in } & { g } \left ( 1 \right ) & = - 3 \\ { g } \left ( { - 4 } \right ) &= - 2 8 \hspace { 1.0 in } & { g } \left ( 2 \right ) & = 8 \end {align*} }$$

توجه کنید که اکسترمم مطلق این تابع، شامل نقاط ماکزیمم و مینیمم مطلق این تابع هستند. ماکزیمم مقدار در بین این چهار مقدار برابر با عدد $${ 24 }$$ و مینیمم مقدار برابر با $${ - 28 }$$ است. بنابراین می‌توان بیان کرد که نقطه‌ای که تابع در آن برابر با $${ 24 }$$ است، نقطه ماکزیمم مطلق است و با توجه به چهار رابطه بالا، این نقطه برابر با $${ t = - 2 }$$ است. بنابراین ماکزیمم مطلق این تابع در بازه تعیین شده، یکی از نقاط بحرانی این تابع محاسبه شد.

همچنین مینیمم تابع در این بازه مقداری برابر با $${ - 28 }$$ دارد که در نقطه $${ t = - 4 }$$ رخ داده است. این نقطه، نقطه ابتدای بازه تعیین شده در صورت سوال را نشان می‌دهد. بنابراین دو نقطه $${ t = - 4 }$$ و $${ t = - 2 }$$ نقاط اکسترمم مطلق این تابع را به تصویر کشیده‌اند.

بنابراین در این مثال مشاهده شد که نقاط اکسترمم مطلق می‌توانند جز نقاط ابتدا و انتهای بازه و یا نقاط بحرانی تابع باشند. در واقع یکی از بزرگترین اشتباه‌ها که دانش‌آموزان در این قسمت انجام می‌دهند این است که آن‌ها نقاط ابتدا و انتهای بازه را فراموش می‌کنند و تنها به بررسی نقاط بحرانی تابع می‌پردازند.

مثال 2

نقاط اکسترمم مطلق تابع زیر را در بازه $${ \left [ { { 0 } , 2 } \right ] }$$ محاسبه کنید.

$${ \large { g } \left ( { t } \right ) = 2 { { t } ^ 3 } + 3 { { t } ^ 2 } - 1 2 { t } + 4 }$$

توجه کنید که روند محاسبه نقاط اکسترمم مطلق در این مثال، کاملا مشابه با روندی است که در مثال قبل طی شد. بنابراین در ابتدا پیوسته بودن تابع مورد نظر را در بازه $${ \left [ { { 0 } , 2 } \right ] }$$ مورد ارزیابی قرار می‌دهیم. همانطور که بیان شد، با توجه به اینکه تابع مورد نظر به صورت چند جمله‌ای است، بنابراین در بازه تعیین شده نیز پیوسته خواهد بود.

در ادامه به محاسبه نقاط بحرانی این تابع پرداخته می‌شود. این نقاط در مثال قبل محاسبه شدند و برابر با نقاط زیر هستند.

$${ \large t = - 2 }$$

$${ \large t = 1 }$$

توجه کنید که نقطه $${ t = - 2 }$$ در بازه مورد نظر قرار ندارد. بنابراین تنها به بررسی مقدار تابع در نقطه $${ t = 1 }$$ و نقاط ابتدا و انتهای بازه می‌پردازیم. این موضوع در رابطه زیر نشان داده شده است.

$${ \large { g } \left ( 1 \right) = - 3 \hspace { 0.5 in } { g } \left ( 0 \right ) = 4 \hspace { 0.5 in } { g } \left ( 2 \right ) = 8 }$$

بنابراین ماکزیمم مطلق این تابع در بازه مورد نظر برابر با $${ 8 }$$ است که در $${ t = 2 }$$ رخ می‌دهد و همچنین مینیمم مطلق تابع در بازه مورد نظر، مقداری برابر با $${ - 3 }$$ دارد که این مقدار در نقطه $${ t = 1 }$$ رخ داده است.

توجه کنید که محاسبه نقاط اکسترمم مطلق یک تابع ممکن است پیچیده‌تر از شرایط ذکر شده در این دو مثال باشد. بنابراین در ادامه به بررسی شیوه محاسبه نقاط اکسترمم مطلق یک تابع سینوسی پرداخته می‌شود.

مثال 3

فرض کنید که مقدار جمعیت یک نوع خاص از حشرات بر حسب زمان با توجه به رابطه زیر محاسبه می‌شود.

$${ \large P \left ( t \right ) = 3 \, t + \sin \left ( { 4 t } \right ) + 1 0 0 }$$

مینیمم و ماکزیمم مقدار جمعیت را در چهار ماه اول مورد محاسبه قرار دهید.

به صورت ریاضی می‌توان بیان کرد که این سوال، به دنبال یافتن مینیمم و ماکزیمم مطلق تابع $${ P \left ( t \right ) }$$ در بازه $${ \left [ { 0 , 4 } \right ] }$$ است. توجه کنید که این تابع در بازه بیان شده به صورت پیوسته است، بنابراین در ابتدا با مشتق گرفتن از این تابع نقاط بحرانی تابع را محاسبه می‌کنیم. مشتق این تابع در رابطه زیر نشان داده شده است.

$${ \large { P } ^ \prime \left ( t \right ) = 3 + 4 \cos \left ( { 4 { t } } \right ) }$$

همانطور که بیان شد، برای یافتن نقاط بحرانی باید به دنبال نقاطی باشیم که مشتق تابع در آن نقاط وجود نداشته باشد و یا مشتق برابر با صفر باشد. با دقت به رابطه بالا متوجه می‌شویم که مشتق این تابع در تمام نقاط وجود دارد، بنابراین باید به دنبال نقاطی باشیم که مشتق تابع در آن نقاط برابر با صفر است. بنابراین داریم:

$${ \large \begin {align*} 3 + 4 \cos \left ( { 4 t } \right ) & = 0 \\ \cos \left ( { 4 t } \right ) & = - \frac { 3 } { 4 } \end {align*} }$$

پاسخ این معادله را می‌توان به صورت زیر بیان کرد.

$$ { \large \begin {array} {* { 2 0 } { c } } { 4 t = 2 . 4 1 8 9 + 2 \pi n , \, \, \, \,n = 0, \pm 1 , \pm 2 , \ldots } \\ { 4 t = 3 . 8 6 4 3 + 2 \pi n , \, \, \, \, n = 0 , \pm 1 , \pm 2 , \ldots } \end {array} } $$

برای یافتن پاسخ نهایی t، به شکل زیر عمل می‌کنیم.

$$ { \large \begin {array} {* { 2 0 } { c } } { t = 0 . 6 0 4 7 + \displaystyle \frac { { \pi n } } { 2 } , \, \, \, \, n = 0 , \pm 1, \pm 2 , \ldots } \\ { t = 0 . 9 6 6 1 + \displaystyle \frac { { \pi n } } { 2 } , \, \, \, \, n = 0 , \pm 1 , \pm 2 , \ldots } \end {array} } $$

توجه کنید که نقاط بالا، تمام نقاط بحرانی این تابع را نشان می‌دهند و ما به دنبال یافتن نقاط بحرانی تابع فوق در بازه نشان داده شده در صورت سوال یعنی $${ \left [ { 0 , 4 } \right ] }$$ هستیم. برای تعیین این نقاط باید nهای متفاوت را در روابط فوق قرار دهیم و مقادیر t را به دست بیاوریم. در ابتدا مقدار n را برابر صفر قرار می‌دهیم. بنابراین داریم:

$${ \large { t } = 0 .6 0 4 7 \hspace { 1.0 in } t = 0 . 9 6 6 1 }$$

این دو نقطه در بازه مورد نظر قرار دارند. در ادامه مقدار n را برابر با یک قرار می‌دهیم. بنابراین داریم:

$${ \large { t } = 0 . 6 0 4 7 + \frac { \pi } { 2 } = 2 . 1 7 5 5 \hspace { 1.0 in } t = 0 . 9 6 6 1 + \frac { \pi } { 2 } = 2 . 5 3 6 9 }$$

این دو نقطه نیز در داخل بازه بیان شده در صورت سوال هستند. در ادامه، n را در روابط داده شده، برابر با دو قرار میدهیم. بنابراین داریم:

$${ \large { t } = 0 . 6 0 4 7 + \pi = 3 .7 4 6 3 \hspace { 1.0 in } t = 0 . 9 6 6 1 + \pi = 4 . 1 0 7 7 }$$

با توجه به مقادیر بالا می‌توان متوجه شد که اولین مقدار در داخل بازه مورد نظر است و مقدار دوم در بازه $${ \left [ { 0 , 4 } \right ] }$$ قرار ندارد. بنابراین 5 نقطه بحرانی برای تابع مورد نظر در بازه $${ \left [ { 0 , 4 } \right ] }$$ به صورت زیر می‌توان نمایش داد.

$${ \large 0 . 6 0 4 7 , \, \, \, 0 . 9 6 6 1 , \, \, \, 2 . 1 7 5 5 , \, \, \, 2 . 5 3 6 9 , \, \, \, 3 . 7 4 6 3 }$$

قدم بعدی این است که مقدار تابع در این نقاط و دو نقطه ابتدا و انتهای بازه $${ \left [ { 0 , 4 } \right ] }$$ را محاسبه کنیم. این موضوع در روابط زیر به خوبی نشان داده شده است.

$${ \large \begin {align*} P \left ( 0 \right) & = 1 0 0 . 0 \hspace { 1.0 in } & P \left ( 4 \right ) & = 1 1 1 . 7 1 2 1 \\ P \left ( { 0 . 6 0 4 7 } \right ) & = 1 0 2 . 4 7 5 6 \hspace { 1.0 in } & P \left ( { 0 . 9 6 61 } \right ) & = 1 0 2 . 2 3 6 8 \\ P \left ( { 2 . 1 7 5 5 } \right ) & = 1 0 7 . 1 8 8 0 \hspace { 1.0 in } & P \left ( { 2 . 5 3 6 9 } \right ) & = 1 0 6 . 9 4 9 2 \\ P \left ( { 3 . 7 4 6 3 } \right ) & = 1 1 1 . 9 0 0 4 & & \end {align*} }$$

با مقایسه مقادیر بالا، متوجه می‌شویم که مقدار 100 برابر با کمترین مقدار است و این مقدار مینیمم مطلق جمعیت حشره‌ها در بازه مورد نظر را نشان می‌دهد و در زمان $${ t = 0 }$$ رخ داده است. نکته مهم دیگری که باید به آن اشاره کرد این است که ماکزیمم مقدار تابع در بازه مورد نظر نیز برابر با مقدار $$111.900$$ است که در زمان $${ t = 3.7463 }$$ رخ داده است.

توجه کنید که در این مثال، در صورتی که ما عبارت $${ 2 \pi n }$$ را در رابطه وارد نمی‌کردیم، تمامی نقاط بحرانی به دست نمی‌آمد و پاسخ درستی نیز به مسئله داده نمی‌شد. برای بررسی دقیق‌تر مبحث اکسترمم مطلق و مطالعه انواع روش‌های یافتن نقاط اکسترمم مطلق، به مثال زیر توجه کنید.

مثال 4

فرض کنید که مقدار موجودی یک حساب در بانک بعد از گذشت t سال مطابق با رابطه زیر به دست می‌آید.

$${ \large A \left ( t \right ) = 2 0 0 0 - 1 0 t { { \bf { e } } ^ { 5 - \frac { { { t ^ 2 } } } { 8} } } }$$

مقدار کمترین و بیشترین موجودی حساب را در طول ۱۰ سال ابتدایی بازگشایی آن به دست آورید.

به صورت ریاضی می‌توان بیان کرد که این مثال به دنبال یافتن نقاط اکسترمم مطلق تابع $${ A \left ( t \right ) }$$ در بازه $${ \left [ { 0 ,1 0 } \right ] }$$ است. توجه کنید که این تابع، یک تابع پیوسته است، بنابراین برای محاسبه نقاط اکسترمم مطلق این تابع، ابتدا به بررسی نقاط بحرانی آن می‌پردازیم. بر این اساس ابتدا از تابع داده شده، مشتق می‌گیریم. این موضوع در رابطه زیر به خوبی به نمایش گذاشته شده است.

$${ \large \begin {align*} A ^ \prime \left ( t \right ) & = - 1 0 { { \bf { e } } ^ { 5 - \frac { { { t ^ 2 } } } { 8 } } } - 1 0 t { { \bf { e } } ^ { 5 - \frac { { { t ^ 2 } } } { 8} } } \left ( { - \frac { t } { 4 } } \right ) \\ & = 1 0 { { \bf { e } } ^ { 5 - \frac { { { t ^ 2 } } } { 8 } } } \left ( { - 1 + \frac { { { t ^ 2 } } } { 4 } } \right ) \end {align*} }$$

ترم اول در رابطه بالا یک عبارت نمایی است که هیچگاه برابر با صفر نخواهد شد. بنابراین مشتق بیان شده تنها در نقاطی صفر است که ترم دوم برابر با صفر باشد. بنباراین داریم:

$${ \large - 1 + \frac { { { t ^ 2 } } } { 4 } = 0 \hspace { 0.25 in } \, \, \, \, \Rightarrow \hspace { 0.25 in } \, \, { t ^ 2 } = 4 \hspace { 0.5 in } \Rightarrow \hspace { 0.25 in } \, \, \, \, t = \pm 2 }$$

نکته بسیار مهمی که باید به آن توجه کرد این است که تنها نقطه $${ t = 2 }$$ در بازه بیان شده قرار داد. بنابراین مقدار تابع در این نقطه و نقاط ابتدا و انتهای بازه $${ \left [ { 0 ,1 0 } \right ] }$$ را محاسبه می‌کنیم. این موضوع در رابطه زیر به خوبی نشان داده شده است.

$${ \large A \left ( 0 \right ) = 2 0 0 0 \hspace { 0.5 in } A \left ( 2 \right ) = 1 9 9 . 6 6 \hspace { 0.5 in } A \left ( { 1 0 } \right ) = 1 9 9 9 . 9 4 }$$

بنابراین همانطور که مشاهده می‌شود، موجودی حساب در زمان آغاز باز کردن حساب یعنی $${ t = 0 }$$ برابر با $${ 2000 }$$ دلار بوده است و دو سال بعد یعنی در $${ t = 2 }$$، موجودی حساب به کمترین مقدار خود در طول ده سال یعنی مقدار $${ 199.66 }$$ دلار می‌رسد. نکته مهم دیگری که می‌توان بیان کرد این است که ماکزیمم مطلق موجودی حساب بانکی در سال دهم اتفاق می‌افتد.

تمام مثال‌هایی که تاکنون به بررسی آن‌ها پرداختیم، شامل مشتق‌هایی بودند که در تمام نقاط وجود داشتند و برای یافتن نقاط بحرانی تنها به بررسی نقاطی می‌پرداختیم که مشتق در آن‌ها برابر با صفر بود. در مثال زیر مدل دیگری از توابع مورد مطالعه قرار خواهد گرفت.

مثال 5

اکسترمم مطلق تابع زیر را در بازه $${ \left [ { - 5 , \, - 1 } \right ] }$$ محاسبه کنید.

$${ \large Q \left ( y \right ) = 3 y { \left ( { y + 4 } \right ) ^ { \frac { 2 } { 3 } } } }$$

تابع مورد نظر در تمام نقاط پیوسته است، بنابراین نقاط موجود در بازه بیان شده، می‌توانند اکسترمم مطلق این تابع در بازه مورد نظر باشند. بر این اساس در ابتدا و برای یافتن نقاط بحرانی تابع فوق، از این تابع مشتق می‌گیریم. این موضوع در رابطه زیر به خوبی نشان داده شده است.

$${ \large \begin {align*} Q ^ \prime \left ( y \right ) & = 3 { \left ( { y + 4 } \right ) ^ { \frac { 2 } { 3 } } } + 3 y \left ( { \frac { 2 } { 3} } \right ) { \left ( { y + 4 } \right ) ^ { - \frac { 1 } { 3 } } } \\ & = 3 { \left ( { y + 4 } \right ) ^ { \frac { 2 } { 3 } } } + \frac { { 2 y } } { { { { \left ( { y + 4 } \right ) } ^ { \frac { 1 } { 3 } } } } } \\ & = \frac { { 3 \left ( { y + 4 } \right ) + 2 y } } { { { { \left ( { y + 4 } \right ) } ^ { \frac { 1 } { 3 } } } } } \\ & = \frac { { 5 y + 1 2 } } { { { { \left ( { y + 4 } \right ) } ^ { \frac { 1 }{ 3 } } } } } \end {align*} }$$

نقاط بحرانی این تابع، شامل نقاطی است در آن‌ها مشتق تابع برابر با صفر باشد یا مشتق تابع در آن نقاط وجود نداشته باشد. بنابراین ریشه صورت و مخرج، نقاط بحرانی تابع را تشکیل می‌دهند. بنابراین دو نقطه بحرانی این تابع به شکل زیر نمایش داده می‌شوند.

$${ \large \begin {align*} y & = - 4 \\ y & = - \frac { { 1 2 } } { 5 } \end {align*} }$$

همانطور که مشاهده می‌شود هر دو نقطه بحرانی به دست آمده در بازه $${ \left [ { - 5 , \, - 1 } \right ] }$$ قرار دارند. بنابراین در ادامه به بررسی مقدار تابع در نقاط بحرانی و نقاط ابتدا و انتهای بازه $${ \left [ { - 5 , \, - 1 } \right ] }$$ می‌پردازیم. این موضوع در رابطه زیر نشان داده شده است.

$${ \large \begin {align*} Q \left ( { - 4 } \right ) & = 0 & \hspace { 0.5 in } & & Q \left ( { - \frac { { 1 2 } } { 5 } } \right ) & = - 9 . 8 4 9 \\ Q \left ( { - 5 } \right ) & = - 1 5 & \hspace { 0.5 in } & & Q \left ( { - 1 } \right ) & = - 6 . 2 4 1 \end {align*} }$$

با توجه به مقادیر بالا متوجه می‌شویم که مینیمم مطلق تابع مورد نظر برابر با $${ - 15 }$$ است که در نقطه $${ y = - 5 }$$ دیده می‌شود. همچنین ماکزیمم مطلق این تابع برابر با $${ 0 }$$ در نظر گرفته می‌شود که در نقطه $${ y = - 4 }$$ رخ داده است.

بنابراین همانطور که در این مطلب بیان شد، محاسبه اکسترمم مطلق از چهار مرحله تشکیل می‌شود و در صورتی که دقت کافی در بررسی هرکدام از مراحل به خرج ندهیم، محاسبه نقاط اکسترمم مطلق با خطا مواجه خواهد شد. این خطاها و انواع مختلف اکسترمم‌ها در مثال‌های این مطلب به خوبی و به صورت دقیق مورد بررسی قرار گرفتند.