چرخ دنده حلزونی – از صفر تا صد

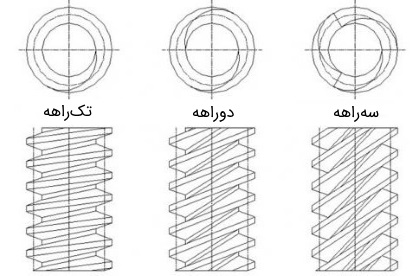
در مقاله چرخ دنده - به زبان ساده، انواع چرخ دنده را معرفی کردیم. هنگامی که نیاز به کاهش زیاد سرعت باشد، چرخ دنده حلزونی راه حل مناسبی است. این نوع چرخ دنده از یک حلزون و یک چرخ حلزون تشکیل شده است. در این حالت، زاویه بین دو محور، ۹۰ درجه است و این دو محور، نسبت به هم متنافرند. معمولاً جنس حلزون از فلزی سخت انتخاب می‌شود. در حالی که چرخ حلزون از جنس فلزات نرمی مانند آلیاژ آلومینیوم برنز است. درگیر شدن حلزون و چرخ حلزون، ترکیبی از غلتش و لغزش را به همراه دارد. حتی در نسبت‌های کاهش زیاد، لغزش بر غلتش غالب می‌شود. در نتیجه، اصطکاک و گرما ایجاد شده و راندمان مجموعه چرخ دنده، پایین می‌آید. وجود لغزش و همچنین به کار بردن فلزهای متفاوت موجب می‌شود چرخ دنده حلزونی به نرمی درگیر شود. بنابراین، در کاربردهایی که باید نویز به حداقل برسد، مانند آسانسور، از چرخ دنده حلزونی استفاده می‌شود. قرقره چوب ماهیگیری و پیچ تنظیم گیتار هم نمونه‌هایی از کاربردهای این نوع چرخ دنده هستند که در شکل زیر، آنها را مشاهده می‌کنید.

نسبت کاهش سرعت در چرخ دنده حلزونی

در بیشتر انواع چرخ دنده‌ها، کاهش دنده به عنوان تابعی از قطر دو چرخ دنده درگیر تعریف می‌شود. اما در نوع حلزونی، این نسبت از روی تعداد راه‌های حلزون و تعداد دندانه‌های چرخ حلزون تعیین می‌شود. به شکل زیر توجه کنید. در حلزون تک‌راهه، هر دور کامل چرخیدن حلزون ($$\large 360$$ درجه)، چرخ دنده را به اندازه یک دندانه پیش می‌برد. بنابراین، به عنوان مثال اگر تعداد دندانه‌های چرخ دنده، $$\large 24$$ تا باشد، نسبت کاهش دنده برابر با $$\large 24:1$$ خواهد بود. نسبت کاهش دنده برای حلزونی که چند راه دارد، با تقسیم تعداد دندانه‌های چرخ حلزون به تعداد راه‌های حلزون تعریف می‌شود.

فیلم آموزش سینماتیک و دینامیک ماشین ها در فرادرس

کلیک کنید

پارامترهای هندسی چرخ دنده حلزونی

پارامترهای هندسی چرخ دنده حلزونی در شکل زیر نشان داده شده است. معمولاً زاویه مارپیچ در حلزون و چرخ حلزون با یکدیگر تفاوت دارند. در بیشتر مواقع، زاویه مارپیچ روی حلزون، بزرگ و زاویه مارپیچ روی چرخ حلزون، کوچک است. زاویه پیشروی حلزون را با $$\large \lambda$$ و زاویه پیشروی چرخ حلزون را با $$\large \psi_G$$ نشان می‌دهیم. همان‌طور که در شکل زیر مشاهده می‌کنید، این دو زاویه متمم هستند. برای مشخص کردن گام در مجموعه چرخ دنده حلزونی، گام محوری را با $$\large p_x$$ و گام دایره‌ای را با $$\large p_t$$ نشان می‌دهیم. اگر زاویه محور ۹۰ درجه باشد، این دو مقدار باهم برابرند. قطر گام در چرخ حلزون همانند چرخ دنده ساده و به صورت $$\large d_G=\frac{N_Gp_t}{\pi}$$ محاسبه می‌شود.

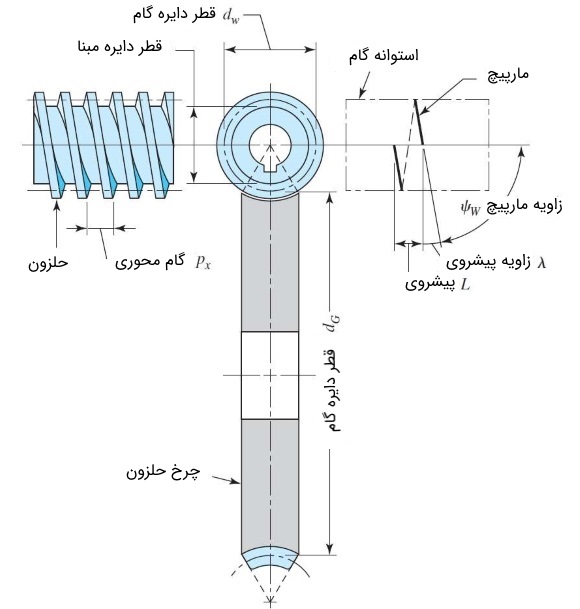
با دقت در شکل درمی‌یابیم که قطر گام حلزون ارتباطی با تعداد دندانه‌های آن ندارد. به طور کلی، قطر گام حلزون در بازه $$\large \frac {C^{0.875}}{3.0} \leq d_W \leq \frac {C^{0.875}}{1.7}$$ قرار می‌گیرد. پارامتر $$C$$ فاصله مرکزی است. در این حالت، ظرفیت اسب بخار چرخ دنده در حالت بهینه قرار می‌گیرد. پیشروی $$L$$ و زاویه پیشروی $$\large \lambda$$ را می‌توان با استفاده از رابطه‌های زیر به هم تبدیل کرد.

$$\large L=p_xN_W,~~~~~\tan\lambda=\frac{L}{\pi d_W}$$

محاسبه نیروها در چرخ دنده حلزونی

شکل زیر را در نظر بگیرید. اگر از اصطکاک صرف نظر کنیم، تنها نیرویی که از چرخ حلزون به حلزون وارد می‌شود $$\large W$$ است. سه مولفه این نیرو در جهت محورهای مختصات نشان داده شده است. با کمک هندسه شکل، این سه مؤلفه را می‌توان به صورت زیر استخراج کرد.

$$\large W^x=W\cos\phi_n\sin\lambda\\~\\
\large W^y=W\sin\phi_n\\~\\
\large W^z=W\cos\phi_n\cos\lambda$$

نیروهایی که به حلزون و چرخ حلزون وارد می‌شوند، به ترتیب با $$W$$ و $$G$$ نشان داده خواهند شد. مؤلفه $$W^y$$، نیروی شعاعی است که به هر دو چرخ دنده وارد می‌شود. فرض می‌کنیم زاویه محور ۹۰ درجه است. در این حالت، نیروی مماسی حلزون $$W^x$$ است. همچنین مؤلفه $$W^z$$ هم نیروی مماسی وارد به حلزون و نیروی محوری وارد به چرخ حلزون را نشان می‌دهد. از آنجایی که نیروهای حلزون و چرخ حلزون در خلاف جهت هم وارد می‌شوند، رابطه‌های زیر را می‌توان نوشت.

$$\large W^x=W_{Wt}=-W_{Ga}\\~\\
\large W^y=W_{Wr}=-W_{Gr}\\~\\
\large W^z=W_{Wa}=-W_{Gt}$$

همان‌طور که مشاهده می‌کنید، محور چرخ حلزون با محور $$x$$ موازی است. محور حلزون هم در راستای محور $$z$$ قرار دارد. در بحث چرخ دنده‌های ساده حرکت یک دندانه نسبت به دندانه‌ای که با آن جفت شده، از نوع غلتشی است. اما در اینجا، حرکت نسبی بین حلزون و چرخ حلزون، کاملاً از نوع لغزشی است. اصطکاک در چرخ دنده حلزونی نقش مهمی ایفا می‌کند و در عملکرد آن مؤثر است. مطابق شکل، هنگامی که نیروی $$W$$ عمود به پروفایل دندانه حلزون وارد می‌شود، نیروی اصطکاکی برابر با $$\large W_f=f\:W$$ ایجاد می‌شود. در نتیجه، مؤلفه‌های سه‌گانه نیروی W با در نظر گرفتن اصطکاک به شکل زیر خواهند بود.

$$\large W^x=W(\cos\phi_n\sin\lambda+f\cos\lambda)\\~\\
\large W^y=W\sin\phi_n\\~\\
\large W^z=W(\cos\phi_n\cos\lambda-f\sin\lambda)$$

با جایگذاری $$\large -W_{Gt}$$ به جای $$\large W^z$$، می‌توان $$\large W_f$$ را با کمک رابطه زیر محاسبه کرد.

$$\large W_f=f\:W=\frac{f\:W_{Gt}}{f\:\sin\lambda\:-\cos\phi_n\cos\lambda}$$

همچنین با مقایسه نیروهای محوری و شعاعی در هر دو چرخ دنده، رابطه زیر بین دو نیروی مماسی حلزون و چرخ حلزون برقرار می‌شود.

$$\large W_{Wt} =W_{Gt}\frac{\cos\phi_n\sin\lambda\: +f\:\cos\lambda}{f\:\sin\lambda - \cos\phi_n \cos\lambda}$$

راندمان چرخ دنده حلزونی

راندمان چرخ دنده حلزونی به صورت نسبت نیروی مماسی وارد به حلزون در حالت بدون اصطکاک به نیروی مماسی وارد به حلزون در حالت با اصطکاک تعریف می‌شود. در حالت اول، $$\large f=0$$ است. در نتیجه با توجه به رابطه قبل، راندمان چرخ دنده حلزونی به صورت زیر به دست می‌آید.

فیلم آموزش طراحی اجزا ۲ – استراتژی حل مساله با حل نمونه سوال در فرادرس

کلیک کنید

$$\large \eta =\frac{\cos\phi_n -f\:\tan\lambda}{\cos\phi_n +f\:\cot\lambda}$$

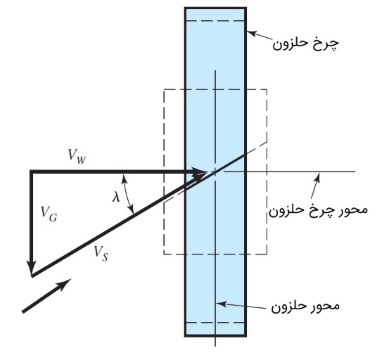
آزمایشات مختلف نشان داده است که ضریب اصطکاک به سرعت لغزشی یا نسبی بستگی دارد. سرعت خطی چرخ حلزون را با $$\large V_G$$ و سرعت خطی حلزون را با $$\large V_W$$ نشان می‌دهیم. در این حالت با توجه به شکل بالا، سرعت نسبی به این صورت قابل محاسبه است.

$$\large V_W=V_G+V_S\\~\\
\large V_S =\frac{V_W}{\cos\lambda}$$

نسبت چرخ دنده حلزونی معمولاً بین $$\large 5:1$$ تا $$\large 75:1$$ تغییر می‌کند. در این حالت، راندمان نیز در بازه 50 تا ۹۰ درصد است. زاویه‌های پیشروی در حلزون و چرخ حلزون براساس جدول زیر طراحی می‌شوند.

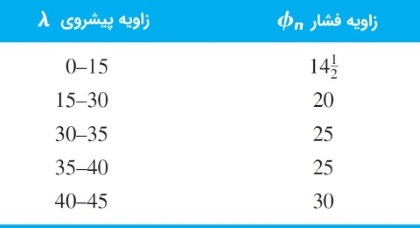
اکنون اگر زاویه پیشروی حلزون را از ۱ تا ۳۰ درجه تغییر دهیم و ضریب اصطکاک را $$\large f = 0.05$$ فرض کنیم، می‌توانیم راندمان چرخ دنده حلزونی را در این حالت‌ها به دست آوریم. این نتایج در جدول زیر ارائه شده است.

مثال

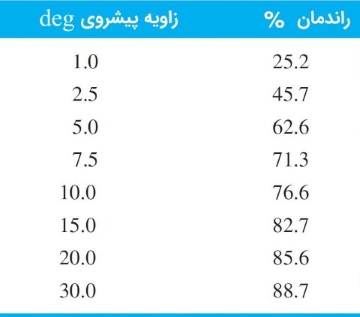
سؤال: چرخ حلزون نشان داده شده در شکل زیر، $$30$$ دندانه دارد. حلزونی راست‌گرد با $$2$$ دندانه، توانی را برابر یک اسب بخار با سرعت $$1200\:rev/min$$ به چرخ حلزون منتقل می‌کند. گام قطری برای چرخ حلزون $$6$$ و عرض دندانه آن $$1$$ است. حلزون دارای قطر دایره گام $$2$$ اینچ بوده و عرض دندانه آن هم $$\large 2\frac{1}{2}$$ اینچ است. زاویه فشار را $$\large 14\frac{1}{2}^\circ$$ فرض کنید. ضریب اصطکاک را برابر ۰/۰۳ در نظر بگیرید. الف) گام محوری، فاصله مرکزی، پیشروی و زاویه پیشروی را محاسبه کنید. ب) گشتاور و نیروهایی را که از طرف یاتاقان‌های $$A$$ و $$B$$ به محور چرخ حلزون وارد می‌شود، به دست آورید.

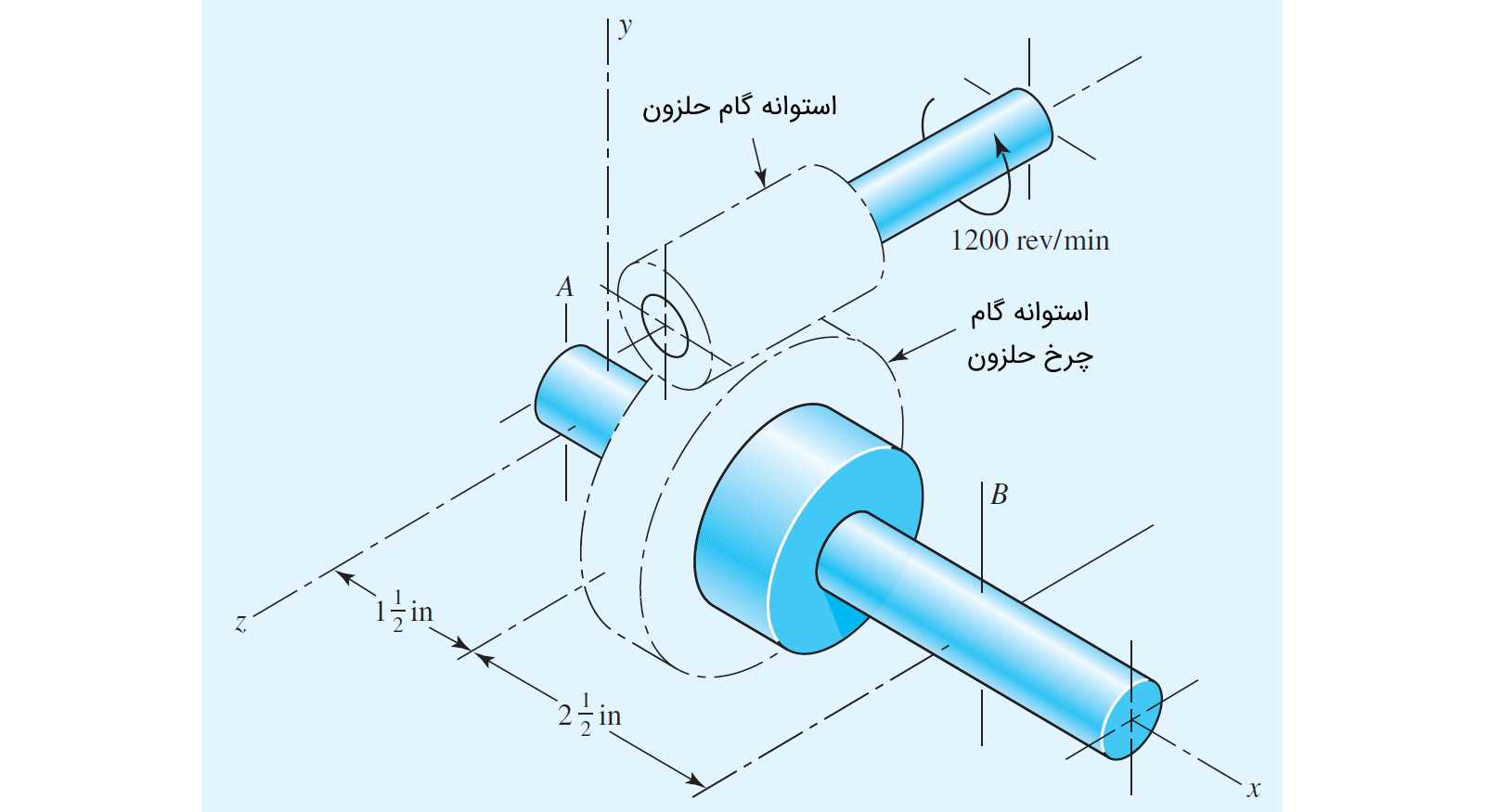
پاسخ: الف) گام محوری مانند گام چرخ دنده، با کمک رابطه زیر محاسبه می‌شود.

$$\large p_x=p_t=\frac{\pi}{P}= \frac{\pi}{6}= 0.524\:in$$

پس از به دست آوردن قطر دایره گام چرخ دنده، فاصله مرکزی به شیوه زیر قابل محاسبه است.

$$\large d_G =\frac{N_G}{P} = \frac{30}{6} = 5\:in\\~\\
\large C= \frac{d_W+d_G}{2} = \frac{2+5}{2} = 3.5\:in$$

برای یافتن مقادیر پیشروی و زاویه پیشروی، به طریق زیر عمل می‌کنیم.

$$\large L = p_xN_W =(0.524)(2) = 1.048\:in\\~\\
\large \lambda = \tan^{-1}\frac{L}{\pi\:d_W} =\tan^{-1} \frac {1.048}{2\pi} = 9.45^\circ$$

ب) می‌دانیم حلزون، راست‌گرد است. حال با توجه به قانون دست راست، با چرخش حلزون، سطح چرخ حلزون در جهت منفی $$z$$ به حرکت درخواهد آمد. بنابراین، چرخ حلزون نسبت به محور $$x$$ در جهت عقربه‌های ساعت می‌چرخد. حال، سرعت خطی حلزون را محاسبه می‌کنیم.

$$\large V_W=\frac {\pi d_Wn_W}{12} = \frac {\pi(2)(1200)}{12} =628\:ft/min$$

سرعت چرخ حلزون برابر با $$\large n_G =(\frac {2}{30})\times1200=80\:rev/min$$ است. بنابراین، سرعت خطی چرخ حلزون به صورت زیر به دست می‌آید.

$$\large V_G= \frac {\pi d_Gn_G}{12} = \frac {\pi (5)(80)}{12} =102\:ft/min$$

اکنون می‌توانیم با داشتن سرعت خطی حلزون و چرخ حلزون، سرعت لغزشی را بیابیم.

$$\large V_S= \frac {V_W}{\cos\lambda} =\frac {628}{\cos 9.46^\circ} =637\:ft/min$$

نیروی مماسی وارد به حلزون، به راحتی و با استفاده از توان اسب بخار و سرعت خطی حلزون، قابل محاسبه خواهد بود. (این رابطه قبلاً در مقاله مربوط به چرخ دنده ساده معرفی شده است.)

$$\large W_{Wt}=\frac {33,000 \times H}{V_W} =\frac {33,000 \times 1}{628} =52.5\:lbf$$

این نیرو در خلاف جهت محور $$x$$ وارد می‌شود. حال با داشتن ضریب اصطکاک، می‌توانیم برآیند نیروی $$W$$ را به دست آوریم.

$$\large W=\frac {W^x}{\cos\phi_n\:\sin\lambda+f\:\cos\lambda}\\~\\
\large =\frac {52.5}{\cos\:14.5^\circ\times\sin9.46^\circ+0.03\times\cos 9.46^\circ} =278\:lbf$$

اکنون مؤلفه‌های $$W$$ در جهت $$y$$ و $$z$$ به راحتی محاسبه می‌شوند.

$$\large W^y=W\sin\phi_n =278\sin14.5^\circ=69.6\:lbf\\~\\
\large W^z=W(\cos\phi_n\cos\lambda-f\:\sin\lambda)\\~\\
\large =278(\cos14.5^\circ\times\cos9.46^\circ+0.03\times\sin9.46^\circ)= 264\:lbf\\~\\
\large \Rightarrow \begin{cases} W_{Ga}=-W^x=52.5\:lbf \\ W_{Gr}=-W^y=-69.6\:lbf \\ W_{Gt}=-W^z=-264\:lbf \end{cases}$$

نمودار جسم آزاد برای این مجموعه چرخ دنده، مطابق زیر رسم شده است.

فیلم آموزش سینماتیک و دینامیک ماشین ها در فرادرس

کلیک کنید

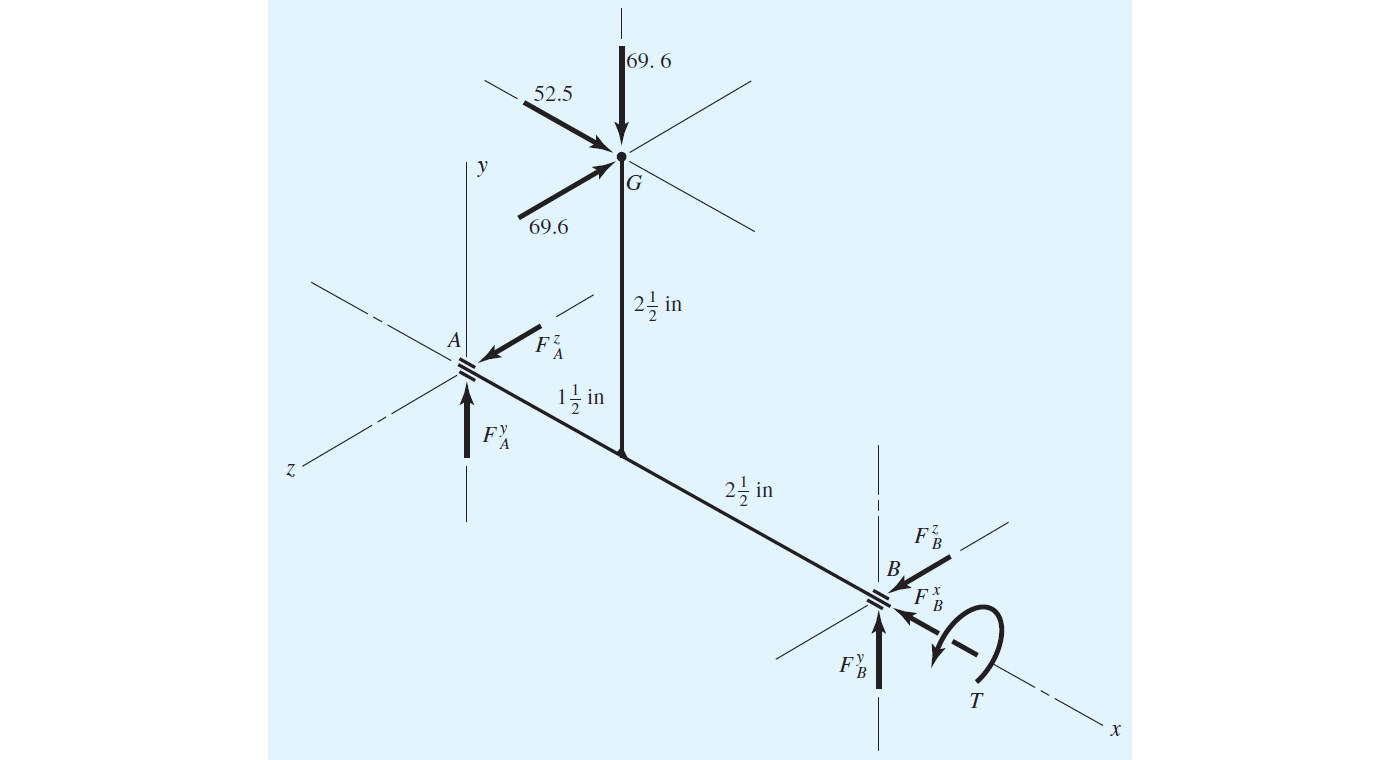
با نوشتن برآیند نیروها در راستای محور $$x$$، مقدار $$\large F_B^x= -52.5\:lbf$$ به دست می‌آید. در ادامه، برآیند گشتاور حول محور $$z$$ را می‌نویسیم.

$$\large -(52.5)(2.5) - (69.6)(1.5) + 4\times F_B^y = 0\\~\\
\large \Rightarrow F_B^y=58.9\:lbf$$

برآیند گشتاور حول محور $$y$$ را نوشته و برابر صفر قرار می‌دهیم.

$$\large (264)(1.5) - 4\times F_B^z = 0~~~~\Rightarrow~~~~F_B^z = 99\:lbf$$

اکنون می‌توانیم تعادل نیروها را در جهت $$y$$ و $$z$$ بنویسیم.

$$\large -69.6 + 58.9 + F_A^y = 0~~~~\Rightarrow~~~~ F_A^y = 10.7 \:lbf\\~\\
\large -264 + 99 +F_A^z =0~~~~ \Rightarrow ~~~~ F_A^z = 165\: lbf$$

در نهایت، گشتاور با کمک رابطه زیر به دست می‌آید.

$$\large -(264)(2.5) + T = 0~~~~\Rightarrow ~~~~ T = 660\:lbf.in$$

به دلیل وجود اصطکاک، گشتاور محاسبه شده، از حاصل‌ضرب نسبت چرخ دنده در گشتاور ورودی کمتر است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• چرخ دنده – به زبان ساده
• چرخ دنده ساده – از صفر تا صد
• نسبت چرخ دنده — به زبان ساده