نسبت چرخ دنده و محاسبات آن — به زبان ساده

امروزه در دنیایی زندگی می‌کنیم که تکنولوژی بخشی جداناپذیر از آن را تشکیل داده است. تکنولوژی مدرنی که امروزه با آن سروکار داریم بر مبنای مفاهیمی پایه‌گذاری شده که در ظاهر به نظر بسیار ساده و ابتدایی می‌آیند. دو مورد از این مفاهیم ساده چرخ و چرخ دنده هستند. چرخ دنده قطعه‌ای است که تقریبا در تمامی وسایل حمل و نقل مورد استفاده قرار می‌گیرد. جالب است بدانید که در تلفن همراهی که شما استفاده می‌کنید نیز از چرخ دنده بهره گرفته شده. با توجه به اهمیت این قطعه، در این مطلب قصد داریم تا نحوه محاسبه نسبت چرخ دنده را توضیح دهیم. البته پیشنهاد می‌کنیم قبل از مطالعه، مطلب حرکت دایره‌ای را به منظور درک بهتر این مطلب مطالعه فرمایید.

محاسبه نسبت چرخ دنده

چرخ دنده، قطعه‌ای است دوار که تعدادی دندانه روی خودش دارد. این قطعه با قطعه‌ای مشابه با خودش تداخل داشته و به این طریق منجر به انتقال قدرت، تغییر جهت دوران یا تغییر سرعت دوران می‌شود. در ادامه، انیمیشنی از تداخل دو چرخ دنده ساده نشان داده شده است.

توجه داشته باشید در روابط از Teeth به عنوان نماد تعداد دندانه و RPM به عنوان نماد سرعت زاویه‌ای استفاده می‌شود. البته در منابع از نماد N و $$ \large \omega $$ هم به منظور نشان دادن تعداد دندانه و سرعت زاویه‌ای استفاده می‌شود.

فیلم آموزش طراحی اجزا ۲ – استراتژی حل مساله با حل نمونه سوال در فرادرس

کلیک کنید

در ابتدا ساده‌ترین حالت را در نظر می‌گیریم. فرض کنید دو چرخ دنده A و B در تماس با هم هستند. در این صورت رابطه بین سرعت زاویه‌ای و تعداد دندانه‌های آن‌ها به صورت زیر است.

$$ \Large \frac { T e e t h _ { A } } { Te e t h _ { B } } = \frac { R P M _ { B } } { R P M _ { A } } $$

به رابطه فوق نسبت چرخ دنده گفته می‌شود. البته جهت به خاطر سپردن این رابطه می‌توان گفت حاصل ضرب تعداد دندانه‌ها و سرعت زاویه‌ای برای دو چرخ دنده‌ درگیرِ A و B برابر با عدد ثابتی است. در حقیقت می‌توان رابطه بالا را به صورت زیر بیان کرد.

$$ \Large R P M _ { A } \times T e e t h _ { A } = R P M _ { B } \times T e e t h_ { B } $$
رابطه ۱

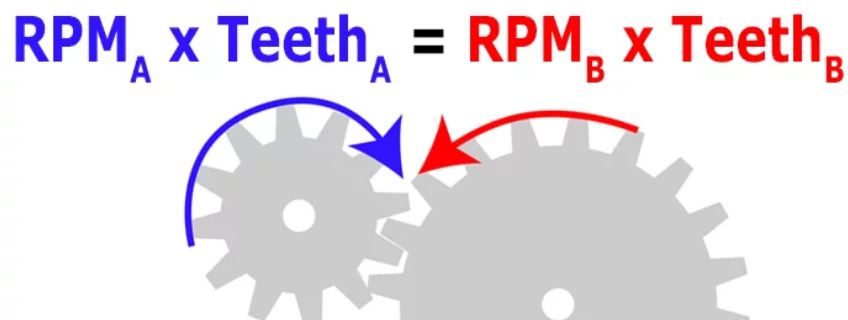
بنابراین با افزایش یا کاهش تعداد دندانه‌ها می‌توان سرعت یک چرخ دنده را افزایش یا کاهش داد. همان‌طور که از شکل بالا نیز بر می‌آید، توجه داشته باشید که در هنگام تداخل دو چرخ دنده، جهت دوران آن‌ها نیز تغییر می‌کند.

مثال ۱

محوری که روی آن چرخ دنده‌ای نیز نصب شده، با سرعت $$ \large 1 8 , 0 0 0 \ \ R P M $$ در حال چرخش است. فرض کنید می‌خواهیم سرعت این محور را به $$ \large 5, 0 0 0 R P M $$ کاهش دهیم. بدین منظور از چرخ دنده‌ی دوم استفاده می‌کنیم. نسبت چرخ دنده مورد نیاز چقدر است؟

بدیهی است که برای کاهش سرعت باید از چرخدنده‌ای با تعداد دندانه‌های بیشتری استفاده شود. بنابراین می‌توان گفت:

$$ \Large \frac { T e e t h _ { A } } { T e e t h _ { B } } = \frac { 5 , 0 0 0 R P M } { 1 8 , 0 0 0 R P M } $$

بنابراین نسبت چرخ دنده برابر است با:

$$ \Large \frac { T e e t h _ { B } } { T e e t h _ { A } } = 3 . 6 $$

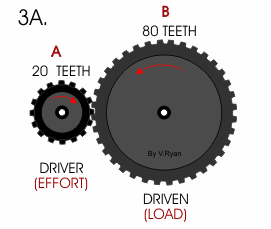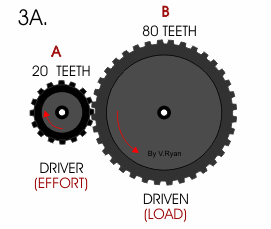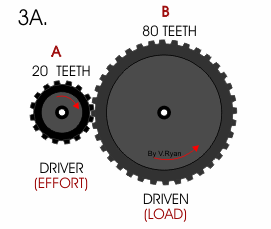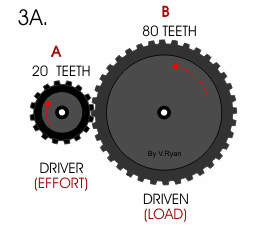
در شکل زیر درگیری دو چرخ دنده با ۱۶ و ۶۰ دندانه نشان داده شده است.

بنابراین اتصال بالا می‌تواند سرعت ۳۷۵ دقیقه/دور را به ۱۰۰ کاهش دهد.

اتصال چند چرخ دنده

شاید با خود این تصور را داشته باشید که با اضافه کردن چرخ دنده‌های سوم، چهارم و غیره می‌توان سرعت دورانی چرخ دنده اولیه را به صورت نمایی افزایش داد. این تصور اشتباه است، چرا که حاصل ضرب سرعت زاویه‌ای در تعداد دندانه‌ها برای تمامی چرخ دنده‌های درگیر، عددی ثابت است.

فیلم آموزش پروژه محور سالیدورکس – طراحی شفت جعبه دنده در فرادرس

کلیک کنید

در ابتدا فرض کنید سه چرخ دنده A و B و C مطابق با شکل زیر با هم درگیر شده‌اند.

در ابتدا نسبت چرخ دنده را بین دو چرخ دنده A و B به صورت زیر می‌نویسیم.

$$ \Large R P M _ { A } \times Teeth _ { A } = R P M _{ B } \times Teeth _ { B } $$

از طرفی چرخ دنده‌های B و C نیز به طور مستقیم با هم درگیرند؛ بنابراین رابطه فوق را می‌توان بین آن‌‌ها نیز نوشت.

$$ \Large R P M _ { B } \times Teeth _ { B } = R P M_ { C } \times T e e t h _ { C } $$

از دو رابطه فوق می‌توان نتیجه گرفت که حاصل ضرب دندانه در سرعت زاویه‌ای برای هر سه چرخ دنده برابر است. بنابراین می‌توان گفت:

$$ \Large R P M _ {A } \times T e e t h _ { A } = R P M _ { B } \times T e e t h _ { B } = R P M _ { C } \times T e e t h _ { C } $$

به عبارتی رابطه زیر نیز بین دو چرخ دنده A و C به صورت زیر برقرار است.

$$ \Large \frac { T e e t h _ { A } } { T e e t h _ { C } } = \frac { R P M _ { C } } { R P M _ { A } } $$

چرخ دنده ترکیبی

در برخی از موارد دو چرخ‌ دنده به نحوی به هم متصل می‌شوند که عملکرد آن‌ها همچون یک جسم صلب است. در شکل زیر نمونه‌ای از چنین چرخ دنده‌ای با ۱۰ و ۴۲ دندانه نشان داده شده است.

توجه داشته باشید که در هر حالتی که از چرخ دنده فوق استفاده شود، سرعت زاویه‌ای A و B با هم برابر هستند. در حقیقت این ترکیب از چرخ دنده‌ها را می‌توان برای ثابت نگه داشتن سرعت زاویه‌ای و تغییر اندازه چرخ دنده استفاده کرد. برای درک بهتر شکل زیر را در نظر بگیرید.

در این شکل چرخ دنده‌های A و B به طور مستقیم با هم درگیرند. بنابراین رابطه زیر را می‌توان برای آن‌ها نوشت.

$$ \Large R P M _ { A } \times T e e t h _ { A } = R P M _ { B } \times T e e t h _ { B } $$

از طرفی چرخ دنده‌های C و D نیز به طور مستقیم با هم درگیرند. بنابراین با استفاده از مفهوم نسبت چرخ دنده، رابطه زیر را می‌توان برای آن‌ها نوشت.

$$ \Large R P M _ { C } \times T e e t h_ { C } = R P M _{ D } \times T e e t h_ { D } $$

هم‌چنین با توجه به برابر بودن سرعت زاویه‌ای دو چرخ‌دنده B و C سرعت زاویه‌‌ای آن‌ها را به صورت $$ \large R P M _ { B C } $$ نشان می‌دهیم. به این ترتیب دو رابطه بالا را می‌توان به صورت زیر بازنویسی کرد.

$$ \Large R P M _ { A } \times T e e t h _ { A } = R P M _ { B C } \times T e e t h _ { B } $$

$$ \Large R P M _ { B C } \times T e e t h _ { C } = R P M _ { D } \times T e e t h _ { D } $$

نهایتا سرعت چرخ دنده D یا همان خروجی را می‌توان به صورت زیر بدست آورد.

$$ \Large R P M _ { D } = R P M _ { A } \times \frac { T e e t h _ { A } \times { T e e t h _ { C } } }{ T e e t h _ { B } \times T e e t h _ { D } } $$

در این مطلب مفهوم نسبت چرخ دنده برای دو چرخ‌ دنده‌ای که به طور مستقیم درگیر باشند، توضیح داده شد. در مطالب آینده محاسبات مربوط به چرخ‌دنده‌های پیچیده تر همچون حلزونی و مارپیچی را توضیح خواهیم داد.

^^