پخش بار نیوتن رافسون در متلب – از صفر تا صد

در آموزش‌های پیشین مجله فرادرس، با مفاهیم و معادلات پخش بار آشنا شدیم. همچنین روش‌های پخش بار نیوتن رافسون و گوس سایدل را به طور مفصل شرح دادیم. در این آموزش، برنامه‌ پخش بار نیوتن رافسون در متلب را ارائه خواهیم‌ کرد.

قبل از بررسی برنامه‌های متلب، پیشنهاد می‌کنیم آموزش‌های «پخش بار در سیستم قدرت» و «پخش بار نیوتن رافسون» را مطالعه کنید.

در ادامه، خلاصه‌ای از مراحل روش نیوتن رافسون را بیان می‌کنیم.

خلاصه روش نیوتن رافسون

جریان تزریقی هر باس با فرمول زیر محاسبه می‌شود:

$$\large I _ { i } = \sum _ { j = 1 } ^ { n } Y _ { i j } V _ { j } = \sum _ { j = 1 } ^ { n } \left| Y _ { i j } \right| \left| V _ { j } \right| < \theta _ { i j } + \delta _ { j }$$

با استفاده از این جریان، می‌توانیم معادلات پخش توان‌های اکتیو و راکتیو را بنویسیم:

$$\large \begin {array} {l} { P _ { i } ^ { [ k] } = \sum _ { j = 1 } ^ { n } \left| V _ { i }^ { [ k ] } \right| \left| V _ { j } ^ { [ k ] } \right| \left| Y _ { i j } \right| \cos \left( \theta _ { i j } - \delta _ { i } ^ { [ k ] } + \delta _ { j } ^ { [ k ] } \right) } \\ { Q _ { i } ^ { [ k ] } = -\sum _ { i = 1 } ^{ n } \left| V _ { i } ^ { [ k ] } \right| \left| V _ { j } ^ { [k ] } \right| \left| Y _ { i j } \right| \sin \left( \theta _ { i j } -\delta _ { i } ^ { [ k ] } + \delta _ { j } ^ { [ k ] } \right ) } \end {array}$$

در نتیجه، با مسئله به فرم $$f ( x ) = b$$ مواجه خواهیم بود:

$$\large x ^ { [ k ] } = \left[ \begin {array} {c} { \delta ^ { [ k ] } } \\ { V ^ { [ k ] } } \end {array} \right] \quad f \left ( x ^ { [ k ] } \right) = \left[ \begin {array} {c} { P _ { i n j } \left( x ^ { [ k ] } \right) } \\ { Q _ { i n j } \left( x ^ { [ k ] } \right ) } \end {array} \right]$$

در روش نیوتن رافسون، یک حدس اولیه به صورت زیر داریم:

حدس اولیه $$x _ { solution}$$ $$\large x ^ {[0]} =$$          $$\large c = f ( x _ {solution} )$$

با استفاده از این حدس اولیه، می‌توانیم از خطا برای محاسبه یک حدس جدید استفاده کنیم:

$$\large x ^ { [ k + 1 ] } = x ^ { [ k ] } + \frac { c - f \left ( x ^ { [ k ] } \right ) } { \left ( d f \left ( x ^ { [ k ] } \right ) / d x \right ) }$$

مخرج کسر، ژاکوبی است و داریم:

$$\large d f ( x ) / d t \; \; \; \; \Rightarrow \; \; \; \; \left[ \begin {array} {c} { \Delta P } \\ { \Delta Q } \end {array} \right] = \left[ \begin {array} {cc} { \partial P / \partial \delta } & { \partial P / \partial | V | } \\ { \partial Q / \partial \delta } & { \partial Q / \partial | V | } \end {array} \right] \left[ \begin {array} {c} { \Delta \delta } \\ { \Delta | V | } \end {array} \right]$$

الگوریتم پخش بار نیوتن رافسون به طور خلاصه مطابق شکل زیر است.

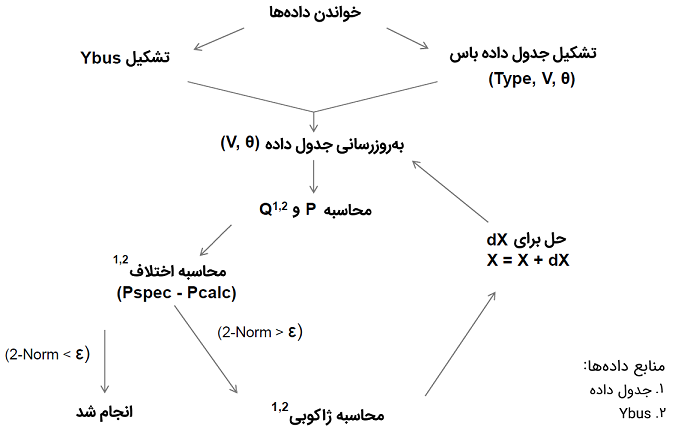
برنامه پخش بار نیوتن رافسون در متلب

برنامه اصلی مربوط به پخش بار نیوتن رافسون powerFlow.m است که در ادامه آورده شده است. قبل از اجرای این برنامه مطمئن شوید فایل‌ها و برنامه‌های زیر در پوشه‌ برنامه باشند:

• فایل BusInputData.csv به عنوان اطلاعات سیستم
• تابع createYbus.m برای تشکیل Ybus از روی فایل اطلاعات BusInputData.csv
• تابع data2bus.m برای ذخیره اطلاعات باس در ساختار جدید برای محاسبات
• تابع findJacob.m برای پیدا کردن ژاکوبی
• تابع sparseAdd.m که در Ybus مورد استفاده قرار می‌گیرد.
• تابع calcPQ.m که محاسبات P و Q‌ را انجام می‌دهد.

فیلم آموزش دیگسایلنت – آنالیز و شبیه سازی سیستم های قدرت با DIgSILENT در فرادرس

کلیک کنید

برنامه‌های فوق را می‌توانید از این لینک [+] دانلود کنید.

درادامه، کد مربوط به هریک از توابع و برنامه‌ها ارائه شده است.

اطلاعات سیستم

فایل ورودی حاوی اطلاعات سیستم BusInputData.csv است که از این لینک [+] قابل دریافت است.

پخش بار نیوتن رافسون

برنامه اصلی پخش بار نیوتن رافسون با عنوان powerFlow.m به صورت زیر است:

تشکیل ماتریس ادمیتانس شین

تابع CreateYbus.m برای تشکیل ماتریس ادمیتانس شین نوشته شده و برنامه آن به شرح زیر است:

برنامه محاسبه P و Q

برنامه محاسبه P و Q، تابعی به نام calcPQ.m است که ورودی‌های آن، Ybus و busData بوده و خروجی‌های Pcalc و Qcalc را نتیجه می‌دهد:

ذخیره اطلاعات باس‌ها در ساختار جدید

تابع data2bus.m برای ذخیره اطلاعات باس در ساختار جدید نوشته شده و به صورت زیر است:

در تابع بالا، از sparseAdd.m استفاده شده که برنامه آن در زیر آمده است:

محاسبه ژاکوبی

تابع محاسبه ماتریس ژاکوبی در findjacob.m نوشته شده و برنامه آن به صورت زیر است:

نتیجه اجرای برنامه

اگر برنامه فوق را اجرا کنیم، نتیجه آن به صورت زیر خواهد بود:‌

NR Power Flow
Code by Chris Mutzel
chris.mutze@gmail.com

Specified Injections
# Pspec Qspec
1.0000 2.9750 0.1420
2.0000 0.1830 0.3730
3.0000 -0.0240 -0.0120
4.0000 -0.0760 -0.0160
5.0000 -0.9420 0.2100
6.0000 0 0
7.0000 -0.2280 -0.1090
8.0000 -0.3000 0.1000
9.0000 0 0
10.0000 -0.0580 -0.0200
11.0000 0 0.2400
12.0000 -0.1120 -0.0750
13.0000 0 0.2400
14.0000 -0.0620 -0.0160
15.0000 -0.0820 -0.0250
16.0000 -0.0350 -0.0180
17.0000 -0.0900 -0.0580
18.0000 -0.0320 -0.0090
19.0000 -0.0950 -0.0340
20.0000 -0.0220 -0.0070
21.0000 -0.1750 -0.1120
22.0000 -0.2000 -0.1000
23.0000 -0.1320 -0.1160
24.0000 -0.0870 -0.0670
25.0000 0 0
26.0000 -0.0350 -0.0230
27.0000 0 0
28.0000 0 0
29.0000 -0.0240 -0.0090
30.0000 -0.1060 -0.0190

######################################################
Begin Newton Raphson
Flat Start->

X =

0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

######################################################

Begin Iteration:1

Error, given by 2-norm of Mismatch vector
1.4031


######################################################

Begin Iteration:2

Error, given by 2-norm of Mismatch vector
0.1984


######################################################

Begin Iteration:3

Error, given by 2-norm of Mismatch vector
0.0022


######################################################

Begin Iteration:4

Error, given by 2-norm of Mismatch vector
7.0148e-07


######################################################

Begin Iteration:5

Error, given by 2-norm of Mismatch vector
1.4676e-13

Power Flow Calculation stopped
Error Threshold Reached


Final Solution after 5 iterations is:
# V Theta
1.0000 1.0000 0
2.0000 1.0431 -7.7207
3.0000 0.9976 -10.0036
4.0000 0.9985 -12.2845
5.0000 1.0099 -17.0839
6.0000 1.0011 -14.3498
7.0000 0.9969 -16.0041
8.0000 1.0099 -15.2790
9.0000 1.0069 -18.8849
10.0000 0.9727 -21.3515
11.0000 1.0821 -18.8849
12.0000 1.0094 -20.3683
13.0000 1.0709 -20.3683
14.0000 0.9858 -21.5250
15.0000 0.9722 -21.6170
16.0000 0.9854 -21.0250
17.0000 0.9714 -21.5128
18.0000 0.9594 -22.3195
19.0000 0.9551 -22.5191
20.0000 0.9587 -22.2919
21.0000 0.9492 -22.2157
22.0000 0.9466 -22.3079
23.0000 0.9323 -22.4806
24.0000 0.9316 -22.3575
25.0000 0.9459 -21.3307
26.0000 0.9268 -21.8175
27.0000 0.9639 -20.3923
28.0000 0.9971 -15.1012
29.0000 0.9427 -21.7819
30.0000 0.9305 -22.7836

Line Flows are:
Bus n to Bus m Snm (per unit)
30.0000 + 0.0000i 29.0000 + 0.0000i 0.0057 + 0.0047i
29.0000 + 0.0000i 27.0000 + 0.0000i 0.0079 + 0.0074i
30.0000 + 0.0000i 27.0000 + 0.0000i 0.0135 + 0.0114i
27.0000 + 0.0000i 25.0000 + 0.0000i -0.0052 - 0.0063i
25.0000 + 0.0000i 26.0000 + 0.0000i -0.0025 - 0.0068i
24.0000 + 0.0000i 25.0000 + 0.0000i 0.0054 + 0.0046i
24.0000 + 0.0000i 23.0000 + 0.0000i -0.0007 + 0.0002i
14.0000 + 0.0000i 15.0000 + 0.0000i -0.0005 - 0.0047i
15.0000 + 0.0000i 18.0000 + 0.0000i -0.0039 - 0.0044i
18.0000 + 0.0000i 19.0000 + 0.0000i -0.0011 - 0.0015i
19.0000 + 0.0000i 20.0000 + 0.0000i 0.0013 + 0.0012i
12.0000 + 0.0000i 16.0000 + 0.0000i -0.0039 - 0.0084i
17.0000 + 0.0000i 10.0000 + 0.0000i 0.0009 + 0.0005i
22.0000 + 0.0000i 21.0000 + 0.0000i 0.0005 + 0.0009i
21.0000 + 0.0000i 10.0000 + 0.0000i 0.0048 + 0.0077i
22.0000 + 0.0000i 10.0000 + 0.0000i 0.0053 + 0.0085i
12.0000 + 0.0000i 13.0000 + 0.0000i -0.0002 + 0.0217i
12.0000 + 0.0000i 4.0000 + 0.0000i 0.0469 - 0.0069i
2.0000 + 0.0000i 4.0000 + 0.0000i -0.0272 - 0.0163i
10.0000 + 0.0000i 9.0000 + 0.0000i 0.0143 + 0.0111i
9.0000 + 0.0000i 11.0000 + 0.0000i -0.0001 + 0.0262i
9.0000 + 0.0000i 6.0000 + 0.0000i 0.0264 - 0.0029i
10.0000 + 0.0000i 6.0000 + 0.0000i 0.0393 + 0.0068i
28.0000 + 0.0000i 6.0000 + 0.0000i 0.0043 + 0.0013i
28.0000 + 0.0000i 8.0000 + 0.0000i -0.0010 + 0.0042i
6.0000 + 0.0000i 8.0000 + 0.0000i -0.0054 + 0.0028i
6.0000 + 0.0000i 7.0000 + 0.0000i -0.0095 - 0.0016i
6.0000 + 0.0000i 2.0000 + 0.0000i 0.0395 + 0.0114i
7.0000 + 0.0000i 5.0000 + 0.0000i -0.0063 + 0.0042i
1.0000 + 0.0000i 2.0000 + 0.0000i -0.0463 + 0.0111i
1.0000 + 0.0000i 3.0000 + 0.0000i -0.0570 - 0.0058i
3.0000 + 0.0000i 4.0000 + 0.0000i -0.0131 + 0.0000i
4.0000 + 0.0000i 6.0000 + 0.0000i -0.0119 + 0.0007i
27.0000 + 0.0000i 28.0000 + 0.0000i 0.0295 + 0.0095i
24.0000 + 0.0000i 22.0000 + 0.0000i 0.0002 + 0.0048i
2.0000 + 0.0000i 5.0000 + 0.0000i -0.0563 - 0.0160i
14.0000 + 0.0000i 12.0000 + 0.0000i 0.0069 + 0.0080i
15.0000 + 0.0000i 12.0000 + 0.0000i 0.0073 + 0.0124i
15.0000 + 0.0000i 23.0000 + 0.0000i -0.0046 - 0.0136i
16.0000 + 0.0000i 17.0000 + 0.0000i -0.0028 - 0.0048i
20.0000 + 0.0000i 10.0000 + 0.0000i 0.0052 + 0.0046i

Computation Time for NR-iteration was:
0.28689 seconds
Computation Time for program was:
0.53745 seconds

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• پایداری سیستم قدرت — به زبان ساده
• شبکه عصبی در متلب — از صفر تا صد
• پارامترهای خط انتقال در مهندسی قدرت — به زبان ساده

^^