نیروی مغناطیسی سیم حامل جریان | به زبان ساده

از آنجا که بارها به طور معمول نمی‌توانند از یک رسانا فرار کنند نیروی مغناطیسی ناشی از بارهای در حال حرکت در یک رسانا به خود رسانا منتقل می‌شود و بدین ترتیب یک نیروی مغناطیسی بر سیم حامل جریان وارد خواهد شد. در این مطلب قصد داریم فیزیک نیروی مغناطیسی سیم حامل جریان را بررسی کنیم.

نیروی مغناطیسی سیم حامل جریان

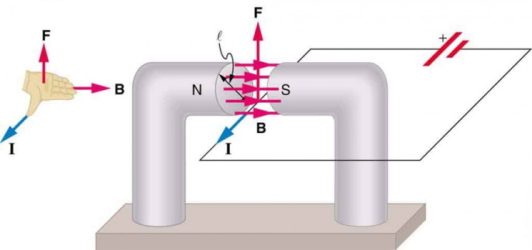
می‌توانیم با در نظر گرفتن مجموع نیروهای مغناطیسی وارد بر بارهای منفرد، عبارتی برای نیروی مغناطیسی موجود در یک جریان بدست آوریم (نیروهایی که در یک جهت و راستا هستند با یکدیگر جمع می‌شوند). نیروی وارد بر یک بار منفرد که با سرعت $$V_{d}$$حرکت می‌کند برابر با $$F=qV_{d}B \sin\theta$$  است. با در نظر گرفتن یکنواخت بودن میدان مغناطیسی $$B$$ در طول سیم $$l$$ و صفر بودن میدان مغناطیسی در جاهای دیگر کل نیروی مغناطیسی روی سیم $$F=qV_{d}B \sin\theta N$$ است که $$N$$ تعداد بارهای حامل جریان در طول $$l$$ است. می‌توان در معادله معرفی شده $$N$$ را برابر با تعداد بارهای حامل جریان در واحد حجم جسم در نظر گرفت که داریم: $$N=nv$$. با توجه به اینکه $$v=Al$$ و A سطح مقطع سیم است پس نیروی وارد شده بر سیم برابر با $$F=(qv_{d}B\sin\theta)(nAl)$$ می‌شود. با مرتب کردن عبارت‌های داخل معادله داریم:

$$F=(nqAv_{d})lB\sin\theta$$

با توجه به این نکته که جریان الکتریکی برابر با $$I=nqAv_{d}$$ است، نیروی مغناطیسی وارد بر سیم رسانای حامل جریان $$I$$ به طول $$l$$ به صورت زیر به دست می‌آید:

$$F=IlB\sin\theta$$

همان‌طور که در شکل زیر نشان داده شده است اگر هر دو طرف این عبارت را بر $$l$$ تقسیم کنیم متوجه می‌شویم که نیروی مغناطیسی در واحد طول سیم در یک میدان یکنواخت برابر است با $$\frac{F}{l}=IB\sin\theta$$.

جهت این نیرو توسط قانون دست راست مشخص می‌شود. در این روش چهار انگشت دست راست را در راستای جریان می‌گیریم و به سمت جهت میدان مغناطیسی خم می‌کنیم در نتیجه جهت انگشت شست نشان‌دهنده نیرو است.

برای تعیین نیروی مغناطیسی $$F$$ بر روی یک سیم با طول و شکل دلخواه اگر مقطع سیم یکنواخت باشد، می‌توان نوشت:

$$F=Il \times B$$

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

کاربردهای نیروی مغناطیسی سیم حامل جریان

از نیروی مغناطیسی روی رساناهای حامل جریان برای تبدیل انرژی الکتریکی به کار استفاده می‌شود (موتورها نمونه بارزی از این کاربرد هستند). Magnetohydrodynamics یا MHD نام فنی‌ است که به یک کاربرد هوشمندانه استفاده از نیروی مغناطیسی داده می‌شود که در آن مایعات بدون اینکه قطعات مکانیکی جابه‌جا شوند، پمپاژ می‌شوند.

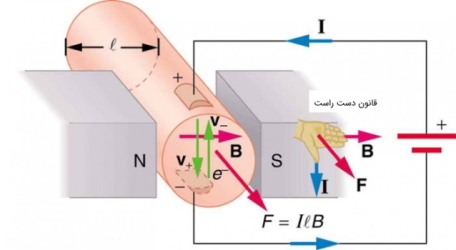
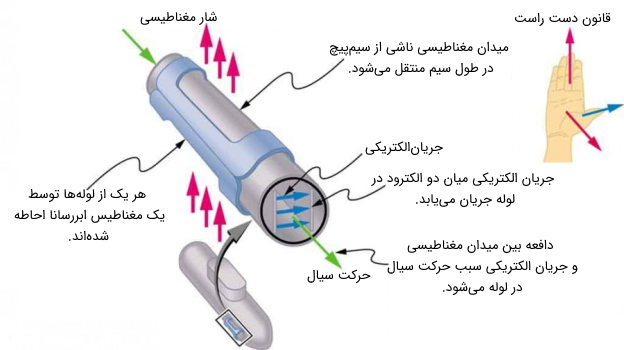
در این وسیله یک میدان مغناطیسی قوی و یک جریان الکتریکی عمود بر میدان مغناطیسی از بالا به پایین لوله‌ای که از مایع پر شده است اعمال می‌شوند. در نتیجه این میدان یک نیرو وارد بر سیال داخل لوله به موازات محور لوله مانند شکل (۳) وجود خواهد داشت.

عدم وجود قطعات متحرک سبب می‌شود که این نیرو برای جابه‌جایی گرما یا عناصر فعال شیمیایی مانند سدیم مایع که در برخی رآکتورهای هسته‌ای استفاده می‌شود کاربرد داشته باشد.

مثال: نیروی وارد شده بر سیم نشان داده شده در شکل (1) را با توجه به داده‌های زیر  محاسبه کنید. طول سیم $$l=5\ cm$$، میدان مغناطیسی $$B=1.5\ T$$ و جریان $$I=20\ A$$.

پاسخ: نیروی وارد بر سیم حامل جریان برابر است با:

$$F=IlB\sin\theta$$

از شکل (۱) می‌توان دید که زاویه بین نیروی مغناطیسی و جریان برابر با $$90$$ درجه است. در نتیجه داریم:

 $$F=IlB\sin\theta=20\times 0.05 \times 1.5\times 1=1.5\ N$$

بنابراین نیروی وارد بر این سیم برابر با ۱٫۵ نیوتن به دست می‌آید. در حقیقت می‌توان بیان کرد که یک میدان مغناطیسی بزرگ نیروی بسیار بزرگی بر یک قطعه کوچک سیم اعمال می‌کند.

اگر در بحث تبدیل یکاهای مثال بالا سوالی ذهنتان را درگیر کرده است مطلب یکاها را قبل از ادامه این مطلب مطالعه کنید.

قلب‌های مصنوعی آزمایشی با استفاده از این روش برای پمپاژ خون در حال آزمایش هستند تا شاید بتوانند اثرات مخرب و مضر پمپ‌های مکانیکی را دور بزنند (با این وجود غشای سلولی باید تحت تاثیر میدان‌های بزرگ MHD قرار بگیرد و این موضوع در کاربرد عملی دستگاه ایجاد تاخیر می‌کند). همچنین نیروی پیشرانه MHD برای زیردریایی‌های هسته‌ای پیشنهاد شده است زیرا می‌تواند نسبت به ملخ‌های معمولی صدای کمتری ایجاد کند.

ارزش زیردریایی‌های هسته ای بر اساس توانایی آن‌ها در پنهان شدن و نجات یافتن از حمله هسته‌ای اول یا دوم است.منظور از حمله هسته ای اول که به آن حمله هسته‌ای پیشگیرانه نیز می‌گویند حمله به زرادخانه هسته‌ای دشمن است که به طور موثر از تلافی جویی در برابر مهاجم جلوگیری می‌کند، همچنین در استراتژی هسته‌ای حمله تلافی جویانه یا توانایی حمله دوم توانایی اطمینان یافته یک کشور در پاسخ به حمله هسته‌ای با تلافی جویی هسته‌ای قدرتمند علیه مهاجم است.

همانطور که زرادخانه های تسلیحات هسته‌ای به آرامی در حال متلاشی شدن توسط دولت‌ها هستند، شاخه زیردریایی هسته‌ای به خاطر توانایی ویژه‌اش که توضیح دادیم، آخرین قسمتی است که خاموش خواهد شد (شکل ۴ را ببینید). همچنین اپراتورهای MHD موجود سنگین و ناکارآمد هستند و به کار و توسعه زیادی نیاز دارند.

مثال‌های نیروی مغناطیسی سیم حامل جریان

مثال ۱: جهت نیروی مغناطیسی روی سیم حامل جریان در هر یک از شش حالت شکل زیر چگونه است؟

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

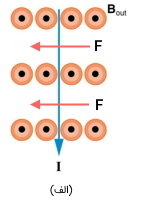
پاسخ: با استفاده از قانون دست راست هر یک از حالت‌ها را بررسی می‌کنیم. قبل از بررسی هر یک از حالت‌ها باید یادآوری کرد که نقطه در مفهوم جهت بردارها به معنای عمود و به سمت خارج صفحه و ضربدر به معنای بردار عمود و به سمت داخل صفحه است.

الف) چهارانگشت دست راست را به سمت جریان بگیرید و در جهت میدان خم کنید (نقطه به معنای بردار عمود و به سمت خارج صفحه است). در نتیجه جهت بردار نیرو به سمت چپ و به صورت زیر است.

ب) چهار انگشت را به سمت شمال که جهت جریان در این حالت است بگیرید و به سمت راست که جهت میدان مغناطیسی است خم کنید. جهت نیرو به سمت داخل صفحه است که به صورت ضربدر در شکل نشان داده‌ایم.

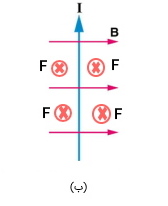
ج) در این حالت جریان به سمت راست است، با خم کردن انگشتان دست راست به سمت داخل صفحه، جهت جریان به سمت بالا خواهد بود.

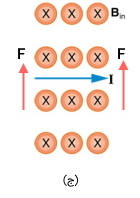
د) همان‌طور که از تصویر مشخص است زاویه بین نیروی مغناطیسی و جریان ۱۸۰ درجه است و مقدار $$\sin 180$$ صفر است. بدین ترتیب نیرو در این حالت صفر است.

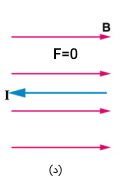
ه) در این حالت جهت جریان به سمت داخل صفحه است با چرخش انگشتان دست راست به سمت جهت میدان مغناطیسی به سمت شمال، جهت نیرو به سمت راست خواهد بود.

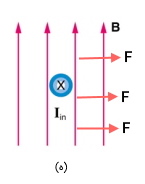
و) جهت نیرو در این حالت به سمت جنوب خواهد بود. زیرا جریان به سمت خارج صفحه و میدان به سمت چپ است، در نتیجه جهت نیرو به سمت جنوب است.

اگر بخواهیم روش‌ بالا را با زبانی راحت بیان کنیم می‌توان گفت در دنیای ما سه جهت یا مولفه مختصات وجود دارد که عبارت از $$y$$ (شمال و جنوب)، $$x$$ (شرق و غرب) و $$z$$ (داخل و خارج صفحه است) هستند. سه بردار $$B$$، $$I$$ و $$F$$ بر هم عمود هستند. به این ترتیب اگر یکی از بردارها در صفحه $$x$$ و دیگری در جهت $$y$$ باشد، بردار سوم در راستای $$z$$ است.حالا تنها لازم است جهت آن بردار را به دست آورید.

نکته دیگر که لازم است مورد توجه قرار دهید این است که ترتیب بردارها در ضرب خارجی بردارها مهم است. به این معنی که ابتدا باید انگشتان شما در جهت جریان باشد و به سمت میدان بچرخانید، عکس این عمل نتیجه درستی را به شما ارائه نمی‌دهد.

مثال ۲: در تصاویر زیر جهت جریان را با توجه به جهت نیروی مغناطیسی که باعث ایجاد نیرو در راستای نشان داده شده در شکل است را مشخص کنید و فرض کنید جریان عمود بر B است؟

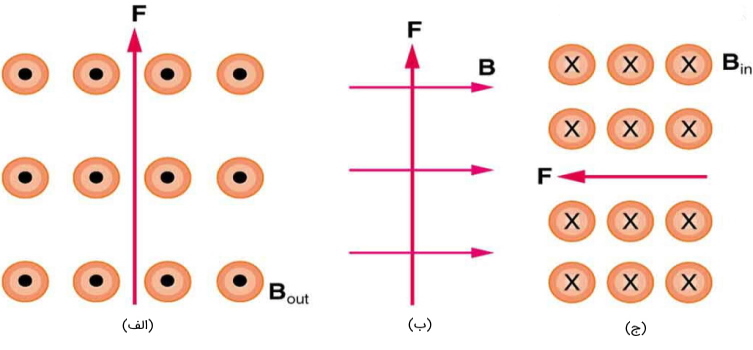
پاسخ:

الف) همان طور که از شکل مشخص است جهت میدان در راستای $$z$$ و جهت نیرو در راستای $$y$$ است. بدین ترتیب جهت جریان در راستای $$x$$ خواهد بود و برای ایجاد نیرویی به سمت شمال لازم است که جهت جریان به سمت چپ باشد.

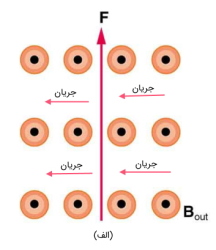
ب) نیروی مغناطیسی در صفحه $$x$$ و میدان در صفحه $$y$$ است. بدین ترتیب جریان در صفحه $$z$$ و به سمت داخل است تا بتواند نیرویی به سمت شمال ایجاد کند.

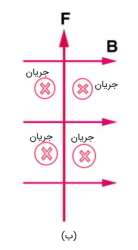
ج) میدان در صفحه $$z$$ و نیرو در صفحه $$x$$ است. بدین ترتیب جریان باید در صفحه $$y$$ و به سمت شمال باشد تا باعث ایجاد نیرویی به سمت چپ شود.

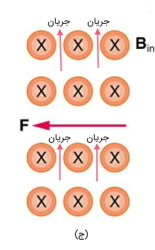
مثال ۳: در تصویر زیر جهت میدان را با این فرض که عمود بر جریان است، رسم کنید.

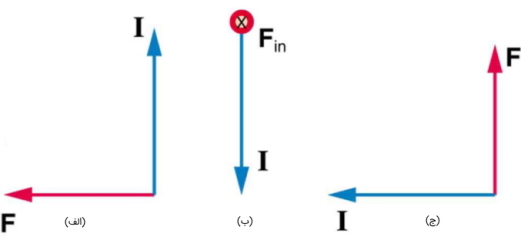
پاسخ

الف) نیرو در صفحه $$x$$ و جریان در صفحه $$y$$ است. بدین ترتیب میدان باید در صفحه $$z$$ باشد و برای ایجاد نیرویی به سمت چپ، جهت آن باید به سمت داخل صفحه باشد.

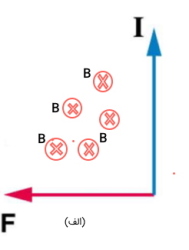
ب) جریان در صفحه $$y$$ و نیرو در صفحه $$z$$ است. در نتیجه میدان در صفحه $$x$$ قرار می‌گیرد و به سمت چپ است تا باعث ایجاد میدانی به سمت داخل صفحه شود.

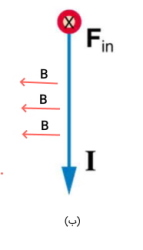
ج) جریان در صفحه $$x$$ و نیرو در صفحه $$y$$ است. در نتیجه میدان باید در صفحه $$z$$ و به سمت خارج صفحه باشد.

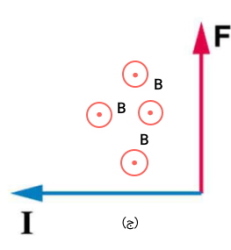
مثال ۴: یک سیم به طول 50 سانتی متر و جرم 10 گرم در یک صفحه افقی توسط یک جفت سرب انعطاف پذیر معلق است. سیم تحت یک میدان مغناطیسی ثابت به بزرگی $$0.5$$ تسلا قرار می‌گیرد که جهت آن در شکل نشان داده شده است. اندازه و جهت جریان در سیم مورد نیاز برای از بین بردن کشش در قطعه سرب‌های نگهدارنده چه قدر است؟

پاسخ: از نمودار آزاد جسم در شکل زیر هنگامی که نیروهای گرانش و مغناطیسی یکدیگر را خنثی کنند تنش‌ در سیم‌های نگهدارنده به صفر می‌رسد. با استفاده از قانون دست راست در می‌یابیم نیروی مغناطیسی به سمت بالا است. پس می‌توانیم جریان $$I$$ را با برابر قرار دادن دو نیرو تعیین کنیم.

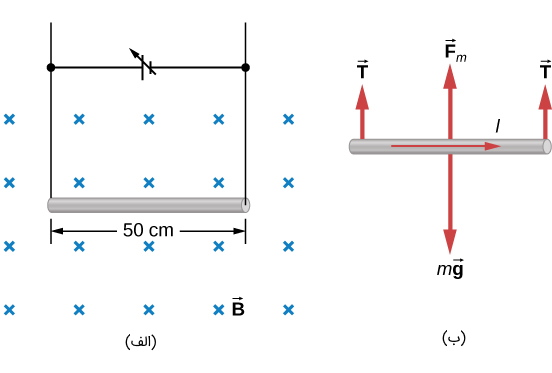
دو نیروی وزن و نیروی مغناطیسی روی سیم را برابر قرار می‌دهیم و داریم:

$$mg = IlB$$

بدین ترتیب خواهیم داشت:

$$I = \frac{mg}{lB} = \frac{(0.010 \, kg}{9.8 \, m/s^2)}{(0.50 \, m)(0.50 \, T)} = 0.39 \, A$$

این میدان مغناطیسی بزرگ برای مقابله با وزن سیم نیروی قابل توجهی بر روی سیم ایجاد می‌کند.

مثال ۵: یک سیم سفت و محکم که در امتداد محور $$y$$ قرار دارد جریان $$5\ A$$ را در جهت مثبت $$y$$ اعمال می‌کند. (الف) اگر یک میدان مغناطیسی ثابت به بزرگی $$0.3\ T$$ در امتداد محور $$x$$ مثبت وارد شود نیروی مغناطیسی در واحد طول سیم چقدر است؟ (ب) اگر یک میدان مغناطیسی ثابت به بزرگی $$0.3\ T$$ و با زاویه $$30$$ درجه در صفحه $$+x$$ و $$+y$$ قرار گیرد، نیروی مغناطیسی در واحد طول سیم چقدر است؟

پاسخ: نیروی مغناطیسی روی سیم حامل جریان در یک میدان مغناطیسی توسط $$\vec{F} = I\vec{l} \times \vec{B}$$ داده می‌شود. برای قسمت (الف) از آنجا که میدان مغناطیسی و جریان در این مسئله عمود بر یکدیگر هستند، می‌توانیم رابطه را ساده کرده و به صورت $$F=IlB$$ مقدار نیرو را به دست آوریم و جهت آن را از طریق قانون دست راست پیدا کنیم. همچنین با تقسیم رابطه بر طول نیرو در واحد طول به دست می‌آید. برای قسمت (ب) حاصلضرب خارجی جریان و میدان را با نوشتن بردارها بر حسب بردار یکه می‌توان محاسبه کرد و بدین ترتیب مقدار نیرو در واحد طول را به دست می‌آوریم.

بدین ترتیب برای قسمت (الف) داریم:

$$F = IlB \, sin \, \theta$$
$$\frac{F}{l} = (5.0 \, A)(0.30 \, T)$$
$$\frac{F}{l} = 1.5 \, N/m.$$

برای به دست آوردن جهت نیرو چهار انگشت را در راستای جریان یا همان $$+y$$ می‌گیریم و در راستای میدان که در این حالت در راستای $$+x$$ است خم می‌کنیم. بدین ترتیب نیرو در جهت محور $$z$$ و به سمت داخل است که به صورت بردارهای یکه با $$k$$ نمایش می‌دهیم و داریم:

$$\frac{\vec{F}}{l} = -1.5 \vec{k} \, N/m.$$

چون راستای داخل محور $$z$$ به صورت قراردادی با منفی نمایش داده می‌شود در جواب بالا یک علامت منفی پشت مقدار نیرو قرار می‌گیرد.

برای قسمت (ب) همانطور که توضیح دادیم از بردار‌های یکه برای نمایش جهت بردار استفاده می‌کنیم و داریم:

$$\vec{F} = I\vec{l} \times \vec{B} = (5.0 A) l\hat{j} \times (0.30 T \, cos(30^o)\hat{i}$$
$$\vec{F}/l = -1.30 \hat{k} \, N/m$$

در این حالت نیز جهت نیرو در راستای بردار $$z$$ و به سمت داخل است.

میدان مغناطیسی بزرگ باعث ایجاد نیروی قابل توجهی در طول سیم می‌شود. هرچه راستای میدان و جریان به یکدیگر نزدیک شوند مقدار نیروی وارد بر طول سیم کوچک می‌شود.

مثال ۶: یک حلقه به شعاع $$R$$ حامل جریان $$I$$ در صفحه $$xy$$ قرار گرفته است. یک میدان مغناطیسی یکنواخت ثابت از حلقه به موازات محور $$y$$ مانند شکل زیر عبور می‌کند. نیروی مغناطیسی را در نیمه بالایی حلقه، نیمه پایینی حلقه و کل حلقه پیدا کنید.

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

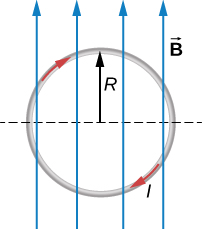
پاسخ: نیروی مغناطیسی روی حلقه فوقانی باید بر حسب دیفرانسیل نیروی وارد بر هر بخش از حلقه نوشته شود. با مجموع دیفرانسیل‌های نیرو در هر قسمت از حلقه می‌توانیم نیرو را برای آن بخش از حلقه به دست آوریم.

با استفاده از رابطه نیروی وارد بر سیم حامل جریان در یک میدان مغناطیسی و استفاده از دیفرانسیل نیرو داریم:

$$dF = I B \, sin \, \theta \, dl$$

که $$\theta$$ زاویه بین جهت میدان مغناطیسی $$+y$$ و سیم است. با قرار دادن دیفرانسیل طول بر حسب شعاع و زاویه داریم:

$$dl = Rd\theta$$
$$dF = IBR \, sin \, \theta \, d\theta$$

برای به دست آوردن نیرو در نیمه بالایی حلقه از رابطه بالا انتگرال می‌گیریم و داریم:

$$F = IBR \int_0^{\pi} sin \, \theta \, d\theta = IBR(-cos \pi + cos 0) = 2 IBR$$

برای نیمه پایینی نیز به همین روش عمل می‌کنیم با این تفاوت که حد انتگرال‌گیری عکس می‌شود و بدین ترتیب داریم:

$$F = IBR \int_{\pi}^0 sin \, \theta \, d\theta = IBR(-cos 0 + cos \pi) = -2 IBR$$

بدین ترتیب نیروی کل وارد بر حلقه که از مجموع نیروی قسمت پایینی و بالایی حلقه به دست می‌آید برابر با صفر خواهد بود. در حقیقت باید بیان کرد که کل نیروی وارد شده به هر حلقه بسته‌ای در یک میدان مغناطیسی یکنواخت صفر است.

مثال ۷: سیمی به طول 150 سانتی متر که دارای جریان الکتریکی $$0.1\ A$$ است در جهت $$x$$های منفی و عمود بر میدان مغناطیسی $$B$$ است به دلیل وجود میدان مغناطیسی سیم نیرویی در جهت $$y$$های مثبت و به اندازه $$6\times 10^{-3}$$ را تجربه می‌کند. الف) اندازه و ب) جهت میدان مغناطیسی را پیدا کنید.

پاسخ: اندازه میدان را می‌توان با استفاده از رابطه نیروی مغناطیسی سیم حامل جریان در میدان مغناطیسی به دست آورد. همچنین جهت میدان با استفاده از قانون دست راست قابل محاسبه است. بدین ترتیب داریم:

$$F=ILB\sin \theta$$
$$\rightarrow1.5\times 0.1 \times B \times 1=6\times 10^{-3}$$
$$\Rightarrow B=\frac{6\times 10^{-3}\ N}{1.5\times 0.1}$$
$$\Rightarrow B=4\times 10^{-2}\ T$$

برای یافتن جهت جریان با استفاده از قانون دست راست با توجه به اینکه نیرو در راستای $$+y$$ و جریان در راستای $$-x$$ است پس جهت میدان در راستای $$z$$ و به سمت خارج خواهد بود. تصویر زیر را ببینید به جهت دستگاه‌های مختصات توجه کنید تا سردرگم نشوید.

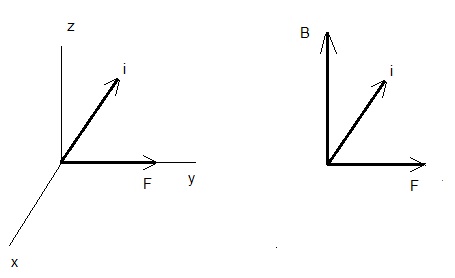
اگر تصور می‌کنید که هنوز در استفاده از قانون دست راست برای پیدا کردن جهت بردارها تبحر کامل را ندارید می‌توانید مطلب قانون دست راست در فیزیک را در مجله فرادرس مطالعه کنید.

جمع‌بندی

در این مطلب نیروی مغناطیسی حاصل از یک سیم حامل جریان الکتریکی در میدان مغناطیسی را بررسی کردیم و جهت بردار نیرو را با استفاده از قانون دست راست برای مثال‌های مختلف به دست آوردیم. در انتهای این مطلب با حل چند مثال تلاش کردیم تا موضوع در ذهن خواننده به خوبی روشن شود.