فرادرس
نویز سفید چیست؟ — راهنمای جامع
«فرایند سفید» (White Processes) یا نویز سفید برای اشاره کردن به فرایندهایی مورد استفاده قرار می‌گیرد که در آن‌ها تمام مولفه‌های فرکانسی، با مقدار توان یکسان وجود دارند. به عبارت دیگر، «چگالی طیف توان» (Power Spectral Density) برای تمام فرکانس‌ها یک مقدار ثابت است. توجه کنید که این مفهوم کاملا با تعریف نور سفید همخوانی دارد؛ زیرا در نور سفید نیز تمام رنگ‌های نور با شدت یکسان وجود دارند. در این مطلب قصد داریم به بررسی مفهوم فرایند سفید یا نویز سفید بپردازیم.
تعریف نویز سفید
فرایند $$ X ( t ) $$ را در صورتی یک فرایند سفید می‌گوییم که دارای چگالی طیفی مسطحی باشد. به عبارت دیگر، $$ \mathcal { S } _ { X } ( f ) $$ برای تمام فرکانس‌های $$ f $$ ثابت باشد.
اهمیت نویز سفید در کاربردهای عملی ناشی از این واقعیت است که «نویز حرارتی» (Thermal Noise) را می‌توان در طول یک بازه وسیع فرکانسی با نویز سفید مدلسازی کرد. نکته مهم دیگر این است که گستره وسیعی از فرایندها وجود دارند که برای توصیف منابع اطلاعاتی مورد استفاده قرار می‌گیرند و می‌توان آن‌ها را به صورت خروجی یک سیستم خطی تغییر ناپذیر با زمان یا LTI مدل کرد که با نویز سفید تحریک شدهاند. در تصویر زیر طیف توان یک فرایند سفید نشان داده شده است.
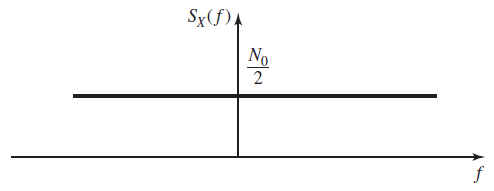
اگر مقدار طیف توان یک فرایند سفید را برابر با $$ \mathcal { S } _ { n } ( f ) = C $$ یعنی یک مقدار ثابت در نظر بگیریم، آن‌گاه مقدار توان فرایند سفید از طریق رابطه زیر برابر با بی‌نهایت به دست می‌آید:
$$ P _ { X } = \int _ { - \infty } ^ { \infty } \mathcal { S } _ { X } ( f ) d f = \int _ { - \infty } ^ { \infty } C d f= \infty $$
واضح است که هیچ کدام از پدیده‌های فیزیکی جهان واقعی نمی‌توانند توان بی‌نهایت داشته باشند. به همین دلیل، فرایند سفید نمی‌تواند یک فرایند فیزیکی واقعی و معنادار باشد. با این حال، آنالیز مکانیک کوانتوم مربوط به نویز سفید نشان می‌دهد که برای محاسبه چگالی طیف توان این سیگنال، می‌توان از رابطه زیر استفاده کرد.
$$ \large \mathcal { S } _ { n } ( f ) = \frac { \hbar f }{ 2 \left ( e ^ { \frac { \hbar f } { K T } } - 1 \right ) } $$
در رابطه فوق، $$ \hbar $$ نشان دهنده «ثابت پلانک» (Planck’s Constant) است که مقداری برابر با $$ 6 .6 × 10 ^ { − 34 } \; \text { Joules × second} $$ دارد. ثابت دیگر در این معادله، $$ K $$ است که «ثابت بولتزمن» (Boltzmann’s Constant) و برابر با $$ 1 .38 × 10 ^ { − 23 } \text { Joules/Kelvin } $$ است. $$ T $$ در معادله فوق نشان دهنده دما بر حسب درجه کلوین است. طیف توان نویز حرارتی در تصویر زیر نشان داده شده است.
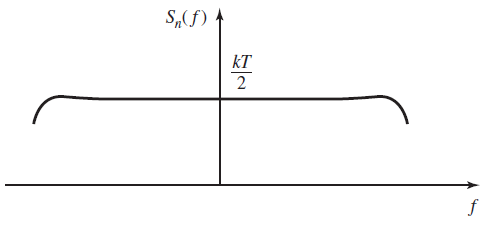
چگالی طیف توان به دست آمده در بالا، در فرکانس صفر هرتز به بیشینه مقدار خود می‌رسد و مقدار بیشنه برابر با $$ \frac { k T } { 2 } $$ است. همچنین زمانی که فرکانس به سمت بی‌نهایت افزایش پیدا کند، چگالی طیف توان به سمت صفر میل خواهد کرد، اما در این حالت، سرعت همگرایی به صفر بسیار آهسته است. به عنوان مثال، در دمای اتاق که برابر با $$ T = 300 K $$ در نظر گرفته می‌شود، مقدار $$ \mathcal { S } _ { n } ( f ) $$ در فرکانس تقریبا $$ f ≈ 2 × 10 ^ { 12 } $$ هرتز به ۹۰ درصد مقدار بیشینه خود افت پیدا می‌کند که این مقدار بسیار فراتر از فرکانس‌های متداول مورد استفاده در سیستم‌های مخابراتی است.
به همین دلیل، نتیجه می‌گیریم که نویز حرارتی (نه دقیقا نویز سفید) را در تمام کاربردهای عملی می‌توان به صورت نویز سفید با طیف توان معادل $$ \frac { k T } { 2 } $$ در نظر گرفت. مقدار $$ k T $$ را همیشه با $$ N _ 0 $$ نشان می‌دهند. بنابراین چگالی طیف توان نویز حرارتی همیشه به صورت $$ \mathcal { S } _ { n } ( f ) = \frac { N _ 0 } { 2 } $$ نمایش داده می‌شود. گاهی به این مقدار، «چگالی طیف توان دو طرفه» (Two-Sided Power Spectral Density) نیز می‌گویند که بر این واقعیت دلالت دارد که طیف هم در فرکانس‌های مثبت و هم در فرکانس‌های منفی گسترده شده است.
حال با در نظر گرفتن تابع «خود همبستگی» (Autocorrelation) مربوط به یک فرایند سفید، داریم:
$$ R _ { n } ( \tau ) = \mathscr { F } ^ { - 1 } \left [ \frac { N _ { 0 } } { 2 } \right ] = \frac { N _ { 0 } } { 2 } \delta ( \tau ) $$
این رابطه نشان می‌دهد که برای تمام مقادیر $$ \tau \neq 0 $$، رابطه $$ R _ { X } ( \tau ) = 0 $$ صحیح است. به عبارت دیگر، اگر در دو نقطه $$ t _ 1 $$ و $$ t _ 2 $$ از یک فرایند سفید نمونه‌برداری کنیم و $$ t _ 1 \neq t _ 2 $$ باشد، متغیر تصادفی به دست آمده «ناهمبسته» (Uncorrelated) خواهد بود. اگر یک فرایند تصادفی علاوه بر سفید بودن، گاوسی نیز باشد، آن‌گاه متغیر تصادفی نمونه برداری شده مستقل نیز خواهد بود.
در نتیجه به صورت خلاصه می‌توان گفت که نویز حرارتی که در مباحث مخابراتی از آن استفاده می‌شود، فرض می‌شود که «ایستا» (Stationary)، «ارگودیک» (Ergodic)، دارای میانگین صفر و فرایند سفید گاوسی باشد که طیف توان آن برابر با $$ \frac { N _ 0 } { 2 } = \frac { k T } { 2 } $$ است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
