مشتق قدر مطلق – به زبان ساده

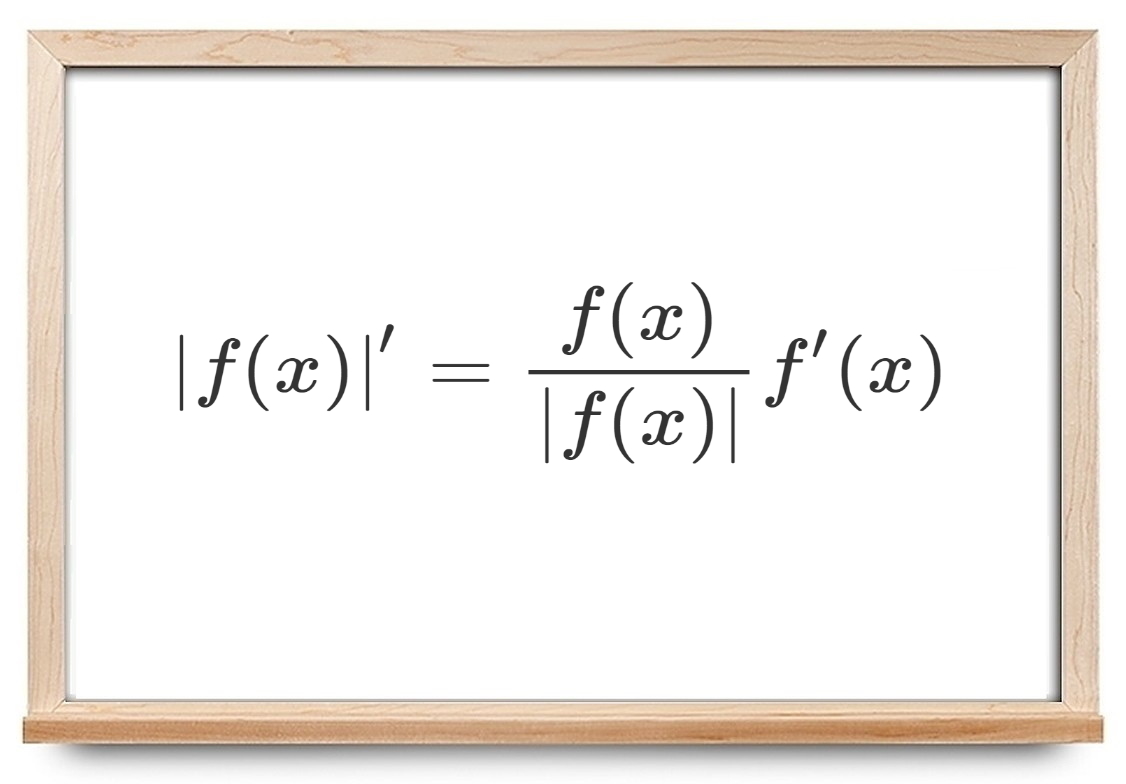
در آموزش‌های پیشین مجله فرادرس، با مفهوم قدر مطلق آشنا شدیم. همچنین، در مطلبی به معادلات و نامعادلات قدر مطلق پرداختیم. در این آموزش یاد می‌گیریم که چگونه مشتق قدر مطلق را محاسبه کنیم.

فرمول مشتق قدر مطلق

تابع $$| f ( x ) |$$ را به عنوان قدر مطلق تابع $$f ( x )$$ در نظر بگیرید. فرمول مشتق $$|f(x)|$$ (برای $$f(x)\neq 0$$) به صورت زیر است:‌

$$\large | f ( x )| ^\prime = \frac { f ( x)} { |f (x)| } f' ( x )$$

در واقع، با یک نمادگذاری دیگر می‌توان چنین گفت که اگر $$u$$ تابعی مشتق‌پذیر از $$x$$ باشد. آنگاه، برای $$u \neq 0$$ داریم:

$$\large \dfrac d { d x } | u | = \dfrac u { | u| } \dfrac {d u} { d x }$$

در $$u = 0$$، تابع $$| u |$$ مشتق‌پذیر نیست.

مشتق قدر مطلق x

طبق فرمولی که در بالا ارائه کردیم، مشتق قدر مطلق $$x$$ برابر است با:

$$\large \begin {align*} | x | ^ { \prime } & = \frac { x } { | x | } \cdot ( x ) ^ { \prime } \\ | x | ^ { \prime } & = \frac { x } { | x | } \cdot ( 1 ) \\ | x | ^ { \prime } & = \frac { x } { |x| } \end{align*}$$

توجه کنید که تابع $$y = |x|' = \frac { x } { | x | }$$ در $$x = 0$$ تعریف نشده است، زیرا مخرج آن را صفر می‌کند. برای رسم نمودار $$y = |x|'$$ می‌توانیم به ازای چند مقدار $$x$$، مقدار $$y$$ متناظر را به دست آوریم و از روی آن نمودار را رسم کنیم.

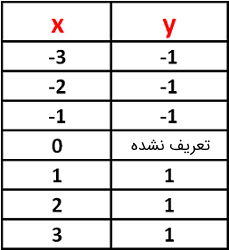
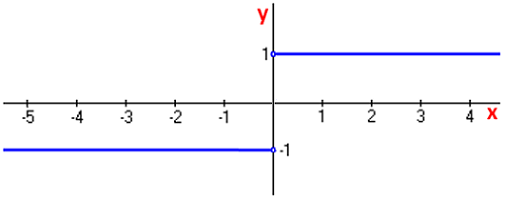
اکنون، براساس جدول بالا می‌توانیم نمودار مشتق $$|x|$$ را رسم کنیم که شکل آن به صورت زیر است.

اثبات فرمول مشتق قدر مطلق x

با توجه به تساوی $$| x | = \sqrt { x ^ 2 }$$، خواهیم داشت:

$$\begin {align*} \frac {d}{ d x } & = \frac { d } { d x } \sqrt { x ^ 2 } = \frac { d } { d x } (x ^ 2 ) ^ \frac 12 \\ & = \frac 12 (x^ 2 ) ^ {-\frac 12} \cdot 2 x = \frac { x } { \sqrt {x^2 }} = \frac { x } { |x|} \end {align*}$$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

اکنون مشتق را در $$x = 0$$ بررسی می‌کنیم. طبق تعریف مشتق، داریم:

$$\large \begin {align*} \dfrac { d | x | } { x} \Bigg \vert _{ x = 0 } & = \lim _{x \to 0 } \frac { | x | - 0 } { x - 0 } \\ & = \begin {cases} \lim _ { x \to 0 ^ + } \dfrac x x & : x > 0 \\ \lim _ { x \to 0 ^ - } \dfrac { - x } x & : x < 0 \end {cases} \\ & = \begin {cases} 1 & : x > 0 \\ -1 & : x < 0 \end{cases} \end {align*}$$

می‌بینیم که حدهای چپ و راست در $$x = 0$$ برابر نیستند و تابع در این نقطه مشتق‌پذیر نیست.

در صورت علاقه به یادگیری روش‌های تعیین مشتق توابع مختلف، مطالعه مطلب «فرمول‌های مشتق مهم + سوال با جواب و دانلود PDF» را به شما پیشنهاد می‌کنیم.

مثال‌های محاسبه مشتق قدر مطلق

در این بخش، مثال‌های متنوعی را از محاسبه مشتق توابع قدر مطلق حل می‌کنیم.

مثال ۱: مشتق $$| 2 x + 1 |$$ را نسبت به $$x$$ به دست آورید.

حل: با استفاده از فرمول مشتق تابع قدر مطلق، داریم:

$$\large \begin {align*} | 2 x + 1 | ^ { \prime } & = \frac { ( 2 x + 1 ) } { | 2 x + 1 | } \cdot ( 2 x + 1 ) ^ { \prime } \\ | 2 x + 1 | ^ { \prime } & = \frac { ( 2 x + 1 ) } { | 2 x + 1 | } \cdot 2 \\ | 2 x + 1 | ^ { \prime } & = \frac { 2 ( 2 x + 1 ) } { | 2 x + 1 | } \end{align*}$$

مثال ۲: مشتق تابع $$| x ^ 3 + 1 |$$ را نسبت به $$x$$ پیدا کنید.

حل: با استفاده از فرمول مشتق تابع قدر مطلق، می‌توان نوشت:

$$\large \begin {align*} \left | x ^ { 3 } + 1 \right | ^ { \prime } & = \frac { \left ( x ^ { 3 } + 1 \right ) } { \left| x ^ { 3 } + 1 \right| } \cdot \left ( x ^ { 3 } + 1 \right ) ^ { \prime } \\ \left | x ^ { 3 } + 1 \right | ^ { \prime } & = \frac { \left ( x ^ { 3 } + 1 \right ) } { \left | x ^ { 3 } + 1 \right | } \cdot 3 x ^ { 2 } \\ \left | x ^ { 3 } + 1 \right | ^ { \prime } & = \frac { 3 x ^ { 2 } \left ( x ^ { 3 } + 1 \right) } { \left | x ^ { 3 } + 1 \right | } \end{align*}$$

مثال ۳: مشتق $$| x | ^ 3$$ را نسبت به $$x$$ بیابید.

حل: از رابطه $$(u^3)' = 3 u^2u'$$ استفاده می‌کنیم و خواهیم داشت:

$$\large \begin {aligned} \left ( | x | ^ { 3 } \right ) ^ { \prime } & = \left \{ 3 | x | ^ { 2 } \right \} \cdot \frac { x} { | x | } \cdot ( x) ^ { \prime } \\ \left ( | x | ^ { 3 } \right ) ^ { \prime } & = \left \{ 3 | x | ^ { 2 } \right \} \cdot \frac { x } { | x | } \cdot ( 1 ) \\ \left ( | x | ^ { 3 } \right ) ^ { \prime } & = 3 x | x | \end{aligned}$$

مثال ۴: مشتق $$| 2 x - 5 |$$ را نسبت به $$x$$ به دست آورید.

حل: با استفاده از فرمول مشتق قدر مطلق جواب به دست می‌آید:‌

$$\large \begin {align*} | 2 x - 5 | ^ { \prime } & = \frac { ( 2 x - 5 ) } { | 2 x - 5 | } \cdot ( 2 x - 5 ) ^ { \prime } \\ |2 x - 5 | ^ { \prime } & = \frac { ( 2 x - 5 ) } { | 2 x - 5 | } \cdot 2 \\ | 2 x - 5 | ^ { \prime } & = \frac { 2 ( 2 x - 5 ) } { | 2 x - 5 | } \end{align*}$$

مثال ۵: مشتق $$( x - 2 ) ^ 2 + | x - 2 |$$ را نسبت به $$x$$ محاسبه کنید.

حل: با استفاده از فرمول مشتق قدر مطلق می‌توان نوشت:

$$\large \begin {align*} \left \{ ( x - 2 ) ^ { 2 } + | x - 2 | \right \} ^ { \prime } & = \left[ ( x - 2 ) ^ { 2 } \right ] ^ { \prime } + | x - 2 | ^ { \prime } \\ \left \{ ( x - 2 ) ^ { 2 } + | x - 2 | \right \} ^ { \prime } & = 2 ( x - 2 ) + \frac { ( x - 2 ) } { | x - 2 | } \cdot ( x - 2 ) ^ { \prime } \\ \left \{ ( x - 2 ) ^ { 2 } + | x - 2 | \right \} ^ { \prime } & = 2 ( x - 2 ) + \frac { ( x - 2 ) } { | x - 2 | } \cdot ( 1 ) \\ \left \{ ( x - 2 ) ^ { 2 } + | x - 2 | \right \} ^ { \prime } & = 2 ( x - 2 ) +\frac { x - 2 } { | x - 2 | } \end{align*}$$

مثال ۶: مشتق $$3 | 5 x + 7 |$$ را نسبت به $$x$$ محاسبه کنید.

حل: با استفاده از فرمول مشتق قدر مطلق جواب به راحتی به دست می‌آید:

$$\large \begin {align*} 3 | 5 x + 7 | ^ { \prime } & = 3 \cdot \frac { ( 5 x + 7 ) } { | 5 x + 7 | } \cdot ( 5 x + 7 ) ^ { \prime } \\ 3 | 5 x + 7 | ^ { \prime } & = 3 \cdot \frac { ( 5 x + 7 ) } { | 5 x + 7 | } \cdot 5 \\ 3 | 5 x + 7 | ^ { \prime } & = \frac { 1 5 ( 5 x + 1 )} { | 5 x + 7 | } \end {align*}$$

مثال ۷: مشتق  $$| \sin x |$$ را نسبت به $$x$$ محاسبه کنید.

حل: با استفاده از فرمول مشتق قدر مطلق داریم:

$$\large \begin {align*} | \sin x | ^ { \prime } & = \frac { \sin x } { | \sin x | } \cdot ( \sin x ) ^ { \prime } \\ | \sin x | ^ { \prime } & = \frac { \sin x } { | \sin x | } \cdot \cos x \\ | \sin x | ^ { \prime} & = \frac { ( \sin x \cdot \cos x ) } { | \sin x | } \end{align*}$$

مثال ۸: مشتق $$| \cos x |$$ را نسبت به $$x$$ محاسبه کنید.

حل: با استفاده از فرمول مشتق قدر مطلق، داریم:

$$\large \begin {align*} | \cos x | ^ { \prime } & = \frac { \cos x } { | \cos x | } \cdot ( \cos x ) ^ { \prime } \\ | \cos x | ^ { \prime } & = \frac { \cos x } { | \cos x | } \cdot(-\sin x ) \\ | \cos x | ^ { \prime } & = \frac { - ( \sin x \cdot \cos x ) } { | \cos x | } \end{align*}$$

مثال ۹: مشتق تابع $$| \tan x |$$ را به دست آورید.

حل: با استفاده از فرمول بالا، به راحتی داریم:

$$\large \begin {align*} | \tan x | ^ { \prime } & = \frac { \tan x } { | \tan x | } \cdot ( \tan x ) ^ { \prime } \\ | \tan x | ^ { \prime } & = \frac { \tan x } { | \tan x | } \cdot \sec ^ { 2 } x \\ | \tan x | ^ { \prime } & = \frac { \sec ^ { 2 } x \cdot \tan x } { | \tan x | } \end{align*}$$

مثال ۱۰: مشتق تابع $$| \sin x + \cos x |$$ را نسبت به $$x$$ محاسبه کنید.

حل: با استفاده از فرمول بالا، داریم:

$$\large \begin {align*} | \sin x + \cos x | ^ { \prime } & = \frac { ( \sin x + \cos x ) } { | \sin x + \cos x | } \cdot ( \sin x + \cos x ) ^ { \prime } \\ | \sin x + \cos x | ^ { \prime } & = \frac { ( \cos x + \sin x ) } { | \sin x+\cos x | } \cdot ( \cos x - \sin x ) \\ | \sin x + \cos x | ^ { \prime } & = \frac {\left ( \cos ^ { 2 } x - \sin ^ { 2 } x \right ) } { | \sin x + \cos x | } \\ | \sin x + \cos x | ^ { \prime } & = \frac { \cos 2 x } { | \sin x + \cos x | } \end {align*}$$