مساحت در مختصات قطبی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

پیش‌تر در بلاگ فرادرس در مورد مختصات‌های قطبی، استوانه‌ای و کروی صحبت کردیم. هدف اصلی از ارائه این مفاهیم، انجام محاسبات راحت‌تر است. برای نمونه می‌توان مساحت یک رویه یا حجم محصور توسط یک صفحه را به راحتی در این مختصات‌ها محاسبه کرد. از این رو در این مطلب قصد داریم تا روش محاسبه مساحت در مختصات قطبی را توضیح دهیم.

مساحت محصور شده

هدف اصلی از ارائه این مطلب آشنایی با نحوه محاسبه مساحت محصور به یک منحنی در مختصات قطبی است.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

توجه داشته باشید که استفاده از کلمه محصور به معنای آن است که مساحت قرار گرفته در یک ناحیه بسته، مد نظر است. برای نمونه ناحیه سبز رنگِ نشان داده شده در شکل زیر، توسط سه تابع $$\theta = \alpha , \theta = \beta$$ و $$r = f ( \theta )$$ محصور شده است.

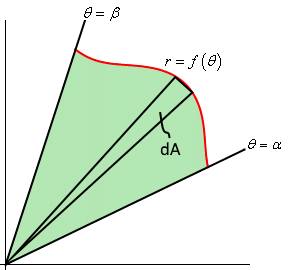
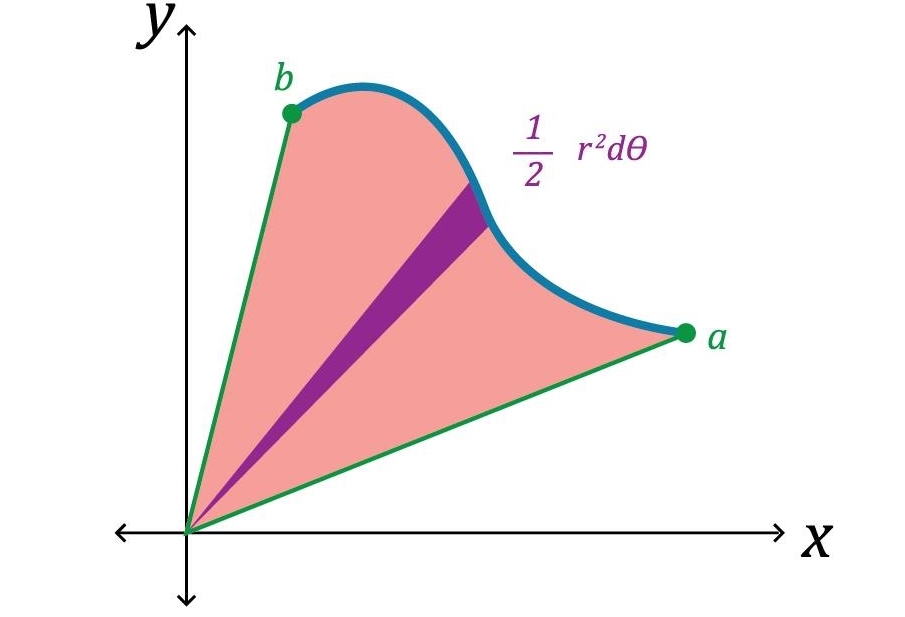
مطابق با شکل فوق، مساحت دیفرانسیل dA برابر با $$\frac { 1 } { 2 } ( r d \theta ) r = \frac { 1 } { 2 } r ^ 2 d \theta$$ است. از این رو اگر از این دیفرانسیل در فاصله $$\alpha$$ تا $$\beta$$ انتگرال گرفته شود، مساحت کل ناحیه بدست خواهد آمد. بنابراین مساحت قسمت سبز رنگ برابر است با:

$$\large A = \int _ { { \, \alpha } } ^ { { \, \beta } } { { \frac { 1 } { 2 } { r ^ 2 } \, d \theta } }$$

توجه داشته باشید که در رابطه فوق از r به جای $$f ( \theta )$$ استفاده شده است. در ادامه مثال‌هایی ذکر شده که مطالعه آن‌ها را توصیه می‌کنیم.

مثال ۱

مساحت حلقه داخلی نمودار $$r = 2 + 4 \cos \theta$$ را بدست آورید.

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

به منظور محاسبه مساحت محصور در نمودار قطبی، در ابتدا بایستی شکل نمودار به درستی ترسیم شود. با صفر قرار دادن معادله مذکور، زاویه‌هایی که در آن‌ها شعاع برابر با صفر شده، مشخص می‌شود. با صفر قرار دادن شعاع، داریم:

$$\large \begin {align*} 0 & = 2 + 4 \cos \theta \\ \cos \theta & = - \frac { 1 } { 2 } \hspace {0.5in} \Rightarrow \hspace {0.5in} \theta = \frac { { 2 \pi } } { 3 } ,\frac{ { 4 \pi } } { 3 } \end {align*}$$

شکل نمودار در ادامه ترسیم شده است.

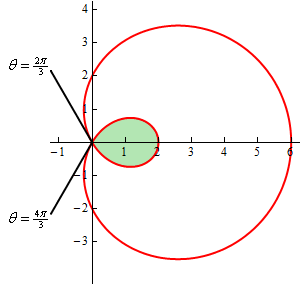
به منظور حدس زدن شکل یک نمودار قطبی می‌توانید در چند نقطه مقادیر r را بدست آورده، سپس شکل کلی نمودار قابل ترسیم است. توجه داشته باشید که زوایای بدست آمده، زوایایی هستند که در آن‌ها حلقه داخلی شروع شده و نهایتا به اتمام می‌رسند. بنابراین مساحت ناحیه نشان داده شده برابر است با:

$$\large \begin {align*} A & = \int _ { { \, \frac { { 2 \pi } } { 3 } } } ^ { { \, \frac { { 4 \pi } } { 3 } } }{ { \frac { 1 } { 2 } { { \left ( { 2 + 4 \cos \theta } \right ) } ^ 2 } \, d \theta } } \\ & = \int _ { { \, \frac { { 2 \pi } } { 3 } } } ^ { { \, \frac { { 4 \pi } } { 3 } } } { { \frac { 1 } { 2 } \left ( { 4 + 1 6 \cos \theta + 1 6 { { \cos } ^ 2 } \theta } \right ) \, d \theta } } \\ & = \int _ { { \, \frac { { 2 \pi } } { 3 } } } ^ { { \, \frac { { 4 \pi } } { 3 } } } { { 2 + 8 \cos \theta + 4\left( {1 + \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \int _ { { \, \frac { { 2 \pi } } { 3 } } } ^ { { \, \frac { { 4 \pi } } { 3 } } } { { 6 + 8 \cos \theta + 4 \cos \left ( { 2 \theta } \right ) \, d \theta } } \\ & = \left. {\left( {6\theta + 8\sin \theta + 2\sin \left( {2\theta } \right)} \right)} \right|_{ \frac { { 2 \pi } } { 3 } } ^ { \frac { { 4 \pi } }{ 3 } } \\ & = 4 \pi - 6 \sqrt 3 = 2 . 1 7 4 \end {align*}$$

اما حالتی دیگر نیز وجود دارد که در آن مقصود محاسبه مساحت بین دو نمودار است. این حالت را در ادامه توضیح خواهیم داد.

مساحت محصور بین دو نمودار

در شکل زیر مساحت محصور بین دو نمودار نشان داده شده است.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

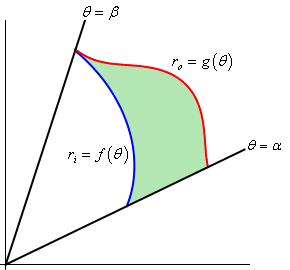
در این حالت می‌توان با استفاده از فرمول ارائه شده در قسمت قبل مساحت دو نمودار را محاسبه کرده و سپس آن‌ها را از هم کم کرد. بنابراین رابطه مربوط به مساحت در این حالت برابر است با:

$$\large A = \int _ { { \, \alpha } } ^ { { \, \beta } } { { \frac { 1 } { 2 } \left ( { r _ o ^ 2 - r _ i ^ 2 } \right ) \, d \theta } }$$

اجازه دهید تا به بررسی یک مثال در این زمینه بپردازیم.

مثال ۲

مساحت محصور شده بین دو نمودار $$r = 3 + 2 \sin \theta$$ و $$r = 2$$ را بیابید. در ابتدا نمودار دو تابع را مطابق با شکل زیر ترسیم می‌کنیم.

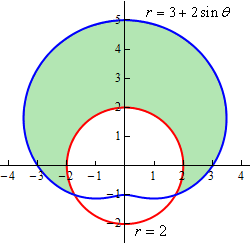
به منظور تعیین مساحت، بایستی محل برخورد دو نمودار را با برابر قرار دادن آن‌ها بدست آورد. از این رو زوایای برخورد دو نمودار برابر است با:

$$\large \begin {align*} 3 + 2 \sin \theta & = 2 \\ \sin \theta & = - \frac { 1 } { 2 } \hspace {0.5in} \Rightarrow \hspace {0.5in} \theta = \frac { { 7 \pi } } { 6 } ,\frac { { 1 1 \pi } } { 6 } \end {align*}$$

در شکل زیر زاویه‌هایی که دو نمودار با هم برخورد کرده، نشان داده شده‌‌اند.

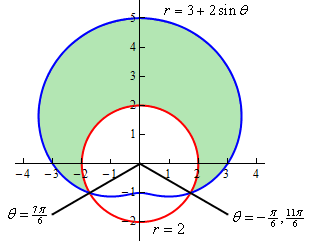
توجه داشته باشید که دو زاویه $$\frac { { 1 1 \pi } } { 6 }$$ و $$- \frac { \pi } { 6 }$$ معادل یکدیگر هستند. به منظور استفاده از فرمول فوق، می‌توان از هر دوی این زوایا استفاده کرد. اما توجه داشته باشید که اگر زاویه از $$\frac{{7\pi }}{6}$$ تا $$\frac{{11\pi }}{6}$$ در نظر گرفته شود، نمی‌تواند تمامی مساحت مدنظر را پوشش دهد. بنابراین اگر این بازه از $$- \frac{{\pi }}{6}$$ تا $$- \frac{{11\pi }}{6}$$ در نظر گرفته شود، می‌تواند تمامی مساحت را پوشش دهد. نهایتا مساحت مد نظر برابر است با:

$$\large \begin {align*} A & = \int _ { { \, - \frac { \pi } { 6 } } } ^ { { \, \frac { { 7 \pi } } { 6 } } }{ { \frac { 1 } { 2 } \left ( { { { \left ( { 3 + 2 \sin \theta } \right ) } ^ 2 } - { { \left ( 2 \right ) } ^ 2 } } \right ) \, d \theta } } \\ & = \int _ { { \, - \frac { \pi } { 6 } } } ^ { { \, \frac { { 7 \pi } } { 6 } } } { { \frac { 1 }{ 2 } \left ( { 5 + 1 2 \sin \theta + 4 { { \sin } ^ 2 } \theta } \right ) \, d \theta } } \\ & = \int _ { { \, - \frac { \pi } { 6 } } } ^ { { \, \frac { { 7 \pi } } { 6 } } } { { \frac { 1 } { 2 } \left ( { 7 + 1 2 \sin \theta - 2 \cos \left ( { 2 \theta } \right ) } \right ) \, d \theta } } \\ & = \left. { \frac { 1 } { 2 } \left ( { 7 \theta - 1 2 \cos \theta - \sin \left ( { 2 \theta } \right ) } \right ) } \right|_{ - \frac{ \pi } { 6 } } ^ { \frac { { 7 \pi } } { 6 } } \\ & = \frac { { 1 1 \sqrt 3 } } { 2 } + \frac { { 1 4 \pi } } { 3 } = 2 4 . 1 8 7 \end {align*}$$

حال اجازه دهید مثال ۲ را از زاویه‌ای دیگر مورد بررسی قرار دهیم.

مثال ۳

مساحت بیرون ناحیه $$r = 3 + 2 \sin \theta$$ و داخل $$r = 2$$ را بیابید.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

با توجه به صورت سئوال، مساحت مذکور برابر با ناحیه سبز رنگ در شکل زیر است.

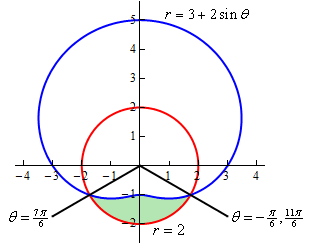
در این حالت زاویه انتگرال‌گیری را بایستی از $$\frac { { 7 \pi } } { 6 }$$ تا $$\frac { { 1 1 \pi } } { 6 }$$ در نظر گرفت. نهایتا مساحت مد نظر برابر است با:

$$\large \begin {align*} A & = \int _ { { \, \frac { { 7 \pi } } { 6 } } } ^ { { \, \frac { { 1 1 \pi } } { 6 } } }{ { \frac { 1 } { 2 } \left ( { { { \left ( 2 \right ) } ^ 2 } - { { \left ( { 3 + 2 \sin \theta } \right ) } ^ 2 } } \right ) \, d \theta } } \\ & = \int _ { { \, \frac { { 7 \pi } } { 6 } } } ^ { { \, \frac { { 1 1 \pi } } { 6 } } } { { \frac { 1 }{ 2 } \left ( { - 5 - 1 2 \sin \theta - 4 { { \sin } ^ 2 } \theta } \right ) \, d \theta } } \\ & = \int _ { { \, \frac { { 7 \pi } } { 6 } } } ^ { { \, \frac { { 1 1 \pi } } { 6 } } } { { \frac { 1 } { 2 } \left ( { - 7 - 1 2 \sin \theta + 2 \cos \left ( { 2 \theta } \right ) } \right ) \, d \theta } } \\ & = \left. { \frac { 1 } { 2 } \left ( { - 7 \theta + 1 2 \cos \theta + \sin \left ( { 2 \theta } \right ) } \right ) } \right|_{\frac { { 7 \pi } }{ 6 } } ^ { \frac { { 1 1 \pi } } { 6 } } \\ & = \frac { { 1 1 \sqrt 3 } } { 2 } - \frac { { 7 \pi } } { 3 } = 2.196 \end {align*}$$

در ادامه مثال ۲ را از زاویه‌ای جدید نگاه می‌کنیم.

مثال ۴

مساحت قرار گرفته در هر دو نمودار $$r = 3 + 2 \sin \theta$$ و $$r = 2$$ را بیابید.

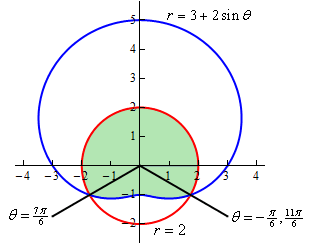
این مساحت را نمی‌توان به طور مستقیم و تنها با استفاده از یک انتگرال محاسبه کرد. دلیل این امر این است که حدودی برای این مساحت قابل تعریف نیست. اما این مساحت را می‌توان با استفاده از دو روش بدست آورد.

روش اول: در این روش مساحت دایره قرمز رنگ محاسبه شده و مساحت بدست آمده در مثال ۳ را از آن کم می‌کنیم. بنابراین می‌توان گفت:

مساحت مثال ۳ - مساحت دایره = مساحت = π×۲^۲-۲.۱۹۶ = ۱۰.۳۷

روش دوم: در این روش می‌توان مساحت محصور در نمودار آبی رنگ را محاسبه کرده و مساحت بدست آمده در مثال ۲ را از آن کم کرد. بنابراین داریم:

مساحت مثال ۲ - مساحت محصور در نمودار آبی = مساحت
$$\large \begin {align*} \\ & = \int _ { { \, 0 } } ^ { { \, 2 \pi } } { { \frac { 1 } { 2 } { { \left ( { 3 + 2 \sin \theta } \right ) } ^ 2 } \, d \theta } } - 2 4 . 1 8 7 \\ & = \int _ { { \, 0 } } ^ { { \, 2 \pi } } { { \frac { 1 }{ 2 } \left ( { 9 + 1 2 \sin \theta + 4 { { \sin } ^ 2 } \theta } \right ) \, d \theta } } - 2 4 . 1 8 7 \\ & = \int _ { { \, 0 } } ^ { { \, 2 \pi } } { { \frac { 1 } { 2 } \left ( { 1 1 + 1 2 \sin \theta - 2\cos \left( { 2 \theta } \right ) } \right ) \, d \theta } } - 2 4 . 1 8 7 \\ & = \left. { \frac { 1 } { 2 } \left ( { 1 1 \theta - 1 2 \cos \left ( \theta \right ) - \sin \left ( { 2 \theta } \right ) } \right ) } \right|_0 ^ { 2 \pi } - 2 4 . 1 8 7 \\ & = 11\pi - 24.187\\ & = 10.370 \end {align*}$$

بدیهی است که استفاده از روش اول راحت‌تر خواهد بود. اما توجه داشته باشید که در برخی از موارد، مجبور خواهیم بود که از روش دوم استفاده کنیم. در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های دروس دبیرستان و پیش‌دانشگاهی
• مختصات قطبی — از صفر تا صد
• ﻣﻌﺎدﻻت دﯾﻔﺮاﻧﺴﯿﻞ ﺑﺎ ﻣﺸﺘﻘﺎت ﺟﺰﺋﯽ — از صفر تا صد
• مختصات استوانه ای — به زبان ساده

^^