مدولاسیون زاویه چیست؟ — از صفر تا صد

در مطالب قبلی مجله فرادرس با اهمیت مدولاسیون و انواع مختلف آن آشنا شدیم. در این مطلب قصد داریم به بررسی یک روش دیگر مدولاسیون بپردازیم که «مدولاسیون زاویه» (Angle Modulation) نام دارد. مدولاسیون زاویه به فرایندی گفته میشود که طی آن فرکانس یا فاز سیگنال حامل منطبق بر سیگنال پیام تغییر میکند.
مدولاسیون زاویه
فرمول استاندار مربوط به مدولاسیون زاویه به صورت زیر است:
که در آن برابر با دامنه سیگنال مدوله شده است که با دامنه سیگنال حامل یکسان در نظر گرفته میشود. همچنین زاویه سیگنال مدوله شده است.
در حالت کلی، روش مدولاسیون زاویه خود به دو گروه «مدولاسیون فرکانس» (Frequency Modulation) و «مدولاسیون فاز» (Phase Modulation) تقسیمبندی میشود:
- مدولاسیون فرکانس: به فرایند تغییر فرکانس سیگنال حامل به صورت خطی و متناسب با سیگنال پیام، مدولاسیون فرکانس میگویند.
- مدولاسیون فاز: به فرایند تغییر فاز سیگنال حامل به صورت خطی متناسب با دامنه سیگنال پیام، مدولاسیون فاز میگویند.
مدولاسیون فرکانس
مدولاسیون فرکانس یا FM در واقع یک روش مدولاسیون زاویه است. در مدولاسیون دامنه یا AM، دامنه سیگنال حامل به صورت متناسب با دامنه سیگنال پیام تغییر میکند. در حالی که در مدولاسیون فرکانس یا FM، فرکانس سیگنال حامل به صورت متناسب با دامنه لحظهای سیگنال مدوله کننده تغییر میکند. به همین دلیل، در مدولاسیون فرکانس، دامنه و فاز سیگنال حامل ثابت و دست نخورده باقی میمانند. در تصویر زیر، نمایی از سیگنالهای پیام، حامل و مدولاسیون فرکانس نشان داده شده است.
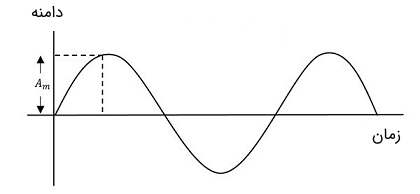
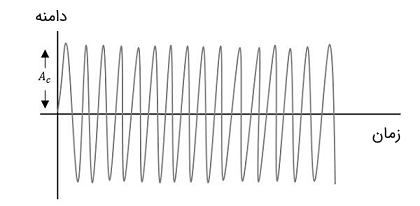
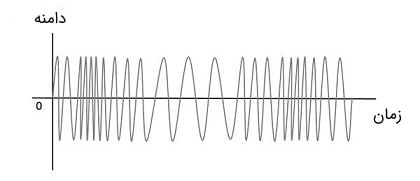
همان طور که در تصویر زیر دیده میشود، هنگامی که دامنه سیگنال پیام افزایش یابد، فرکانس سیگنال حامل نیز متناسب با آن افزایش مییابد و با کاهش دامنه سیگنال پیام، فرکانس سیگنال حامل نیز کاهش مییابد. به این نکته توجه کنید که در صورتی که دامنه سیگنال پیام صفر باشد، فرکانس سیگنال مدوله شده ثابت باقی میماند و برابر با فرکانس سیگنال حامل خواهد بود.
نمایش ریاضی مدولاسیون فرکانس
معادله مربوط به فرکانس لحظهای در مدولاسیون FM به صورت زیر نوشته میشود:
در رابطه فوق برابر با فرکانس سیگنال حامل، حساسیت فرکانسی و سیگنال پیام است. رابطه بین فرکانس زاویهای و زاویه به صورت زیر نوشته میشود:
حال با جایگذاری در معادله فوق، داریم:
حال باید مقدار را در معادله استاندار مربوط به سیگنال مدولاسیون زاویه جایگزین کنیم:
این معادله یک سیگنال مدولاسیون فرکانس یا FM است. حال اگر سیگنال پیام یا مدوله کننده را به صورت زیر در نظر بگیریم:
آن گاه معادله سیگنال مدولاسیون فرکانس به صورت زیر نوشته میشود:
بر اساس سیگنال مدولاسیون فرکانس، کمیت دیگری به نام «شاخص مدولاسیون» (Modulation Index) تعریف میشود که به صورت زیر است:
تفاوت بین فرکانس مدولاسیون FM (فرکانس لحظهای) و فرکانس سیگنال حامل، «انحراف فرکانسی» (Frequency Deviation) نام دارد و با نماد نشان داده میشود که برابر با حاصل ضرب و است. بر اساس مقدار شاخص مدولاسیون، میتوان مدولاسیون فرکانس را به دو نوع «مدولاسیون FM باند باریک» (Narrowband FM) و «مدولاسیون FM پهن باند» (Wideband FM) تقسیمبندی کرد.
مدولاسیون فرکانس باند باریک
مدولاسیون فرکانس باند باریک چند ویژگی دارد که مهمترین آنها عبارتند از:
- این نوع از مدولاسیون فرکانس نسبت به مدولاسیون فرکانس پهن باند، دارای پهنای باند بزرگتری است.
- شاخص مدولاسیون کوچک یا به عبارتی کمتر از یک است.
- طیف فرکانسی این نوع از مدولاسیون فرکانس از سیگنال حامل، باند جانبی بالا و باند جانبی پایین تشکیل شده است.
- از این نوع مدولاسیون در بیسیمهای پلیسی، آمبولانس، تاکسیها و ... استفاده میشود.
مدولاسیون فرکانس پهن باند
در ادامه چند مورد از مهم ترین ویژگیهای مدولاسیون فرکانس پهن باند ذکر شده است:
- این نوع از مدولاسیون فرکانسی دارای پهنای باند بینهایت است.
- شاخص مدولاسیون بزرگ یا به عبارتی بیشتر از یک است.
- طیف فرکانسی این نوع از مدولاسیون فرکانس از سیگنال حامل و تعداد محدودی باند جانبی تشکیل شده است که در اطراف آن قرار گرفتهاند.
- از این نوع مدولاسیون فرکانس عمدتا در کاربردهای سرگرمی و نیز پخش تلویزیون و رادیو FM استفاده میشود.
مدولاسیون فاز
یک نوع دیگر از مدولاسیون زاویه، مدولاسیون فاز یا PM نام دارد. همان طور که دیدیم، در مدولاسیون فرکانس، فرکانس سیگنال حامل به صورت متناسب با دامنه سیگنال پیام تغییر میکند. در حالی که در مدولاسیون فاز یا PM فاز سیگنال حامل به صورت متناظر با دامنه سیگنال پیام تغییر میکند. بنابراین میتوان گفت که در مدولاسیون فاز، دامنه و فرکانس سیگنال حامل ثابت باقی میمانند. در تصاویر زیر سیگنال پیام، سیگنال حامل و سیگنال مدولاسیون فاز یا PM نشان داده شده است.


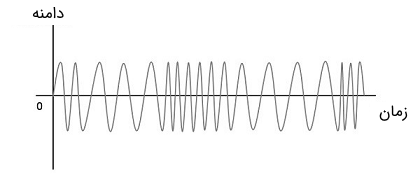
در هر جایی که تغییر فاز در سیگنال رخ داده باشد، فاز سیگنال مدوله شده دارای مقدار بینهایت است. مقدار دامنه لحظهای مربوط به سیگنال مدوله کننده فاز سیگنال حامل را تغییر میدهد. زمانی که دامنه مثبت باشد، فاز در یک جهت تغییر میکند و زمانی که دامنه منفی باشد، فاز در جهت مخالف با آن تغییر میکند.
نمایش ریاضی مدولاسیون فاز
معادله مربوط به فاز لحظهای در مدولاسیون فاز به صورت زیر نوشته میشود:
در رابطه بالا، برابر با حساسیت فاز و برابر با سیگنال پیام است. معادله استاندارد مربوط به مدولاسیون زاویه به صورت زیر است:
حال باید مقدار را در رابطه فوق جایگذاری کنیم. نتیجه به صورت زیر خواهد بود:
معادله فوق مربوط به یک موج مدولاسیون فاز یا PM است. حال اگر سیگنال پیام دارای معادله زیر باشد:
آنگاه معادله سیگنال مدولاسیون فاز به صورت زیر نوشته خواهد شد:
در رابطه فوق، شاخص مدولاسیون به صورت زیر محاسبه میشود:
که در این رابطه برابر با انحراف فاز در نظر گرفته میشود. از مدولاسیون فاز در کاربردهایی نظیر سیستمهای مخابرات موبایل استفاده میشود، در حالی که از مدولاسیون فرکانس عمدتا در پخش FM استفاده میشود.
مثال: مدولاسیون زاویه
در قسمتهای قبل، راجع به پارامترهایی که در مدولاسیون زاویه مورد استفاده قرار میگیرند، بحث کردیم و فرمولهای مربوط به آنها را بیان کردیم. در این قسمت میخواهیم به بررسی یک مثال مربوط به روش مدولاسیون فرکانس از زیرمجموعه مدولاسیون زاویه بپردازیم. یک سیگنال مدوله کننده سینوسی با دامنه ۵ ولت و فرکانس ۲ کیلو هرتز به یک مدولاتور FM اعمال میشود. این مدار مدولاتور دارای حساسیت فرکانسی برابر با ۴۰ هرتز بر ولت است. مقدار پارامترهای انحراف فرکانسی، شاخص مدولاسیون و پهنای باند را محاسبه کنید.
حل
میدانیم که دامنه سیگنال پیام برابر با ، فرکانس سیگنال پیام و حساسیت فرکانسی برابر با است. انحراف فرکانسی بر اساس رابطه زیر به دست میآید:
حال باید مقادیر و را در رابطه بالا جایگذاری کنیم:
در نتیجه مقدار انحراف فرکانسی برابر با ۲۰۰ هرتز به دست میآید. همچنین فرمول مربوط به شاخص مدولاسیون به صورت زیر نوشته میشود:
حال با جایگذاری و در رابطه فوق، شاخص مدولاسیون را به دست میآوریم:
در نتیجه مقدار شاخص مدولاسیون برابر با ۰٫۱ به دست آمده است که کمتر از یک است و به همین دلیل میتوان گفت که این نوع از مدولاسیون فرکانس، جزو مدولاسیون فرکانس باند باریک است. فرمول مربوط به پهنای باند مدولاسیون فرکانس باند باریک دقیقا همانند پهنای باند مدولاسیون AM است:
حال باید مقدار را در رابطه بالا جایگذاری کنیم:
در نهایت، پهنای باند موج مدولاسیون فرکانس باند باریک برابر با ۴ کیلو هرتز به دست میآید.
مثال ۲: مدولاسیون زاویه
یک موج FM با رابطه داده شده است. مقدار انحراف فرکانسی، پهنای باند و توان سیگنال FM را به دست آورید.
حل
میدانیم که معادله استاندارد مربوط به یک سیگنال مدولاسیون فرکانس یا FM به صورت زیر نوشته میشود:
معادله سیگنال مدولاسیون در صورت سوال به صورت زیر است:
حال از طریق مقایسه کردن این دو معادله با همدیگر، مقادیر زیر را میتوان به دست آورد:
- دامنه سیگنال حامل =
- فرکانس سیگنال حامل =
- فرکانس سیگنال پیام =
- شاخص مدولاسیون =
همان طور که میبینیم شاخص مدولاسیون در این جا بزرگتر از یک است و به همین دلیل این مدولاسیون فرکانس از نوع FM پهن باند است. میدانیم که فرمول مربوط به شاخص مدولاسیون به صورت زیر است:
حال معادله فوق را میتوانیم به این صورت بازنویسی کنیم:
مقادیر و را در معادله بالا جایگذاری میکنیم و نتیجه به صورت زیر خواهد بود:
در نتیجه مقدار انحراف فرکانسی برابر با ۹ کیلو هرتز به دست میآید.
فرمول پهنای باند سیگنال مدولاسیون نوع FM پهن باند به صورت زیر نوشته میشود:
مقادیر و را در معادله بالا جایگذاری میکنیم و نتیجه به صورت زیر خواهد بود:
بنابراین پهنای باند سیگنال مدولاسیون FM پهن باند برابر با ۲۰ کیلو هرتز به دست میآید. توان مربوط به سیگنال مدولاسیون فرکانس بر اساس رابطه زیر محاسبه میشود:
حال فرض میکنیم باشد و مقدار را در معادله بالا جایگذاری میکنیم:
بنابراین توان مربوط به یک سیگنال مدولاسیون FM برابر با ۲۰۰ وات به دست می آید.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- دمدولاتور SSBSC — از صفر تا صد
- پهنای باند معادل نویز (ENBW) چیست؟ — از صفر تا صد
- مدولاسیون کد پالس (PCM) چیست؟ — از صفر تا صد
^^












