مدولاتور DSBSC — راهنمای جامع

در مطالب قبلی مجله فرادرس، به بررسی مفاهیم پایه مدولاسیون، مدولاسیون دامنه یا AM، مدولاسیون فاز یا PM و مدولاسیون فرکانس یا FM پرداختیم. همچنین یک نوع خاص از مدولاسیون دامنه را بیان کردیم که مدولاسیون حامل سرکوب شده باند جانبی یا DSBSC نام دارد. در این مطلب قصد داریم به بررسی مدولاتور DSBSC بپردازیم که سیگنال DSBSC را تولید می‌کند.

در حالت کلی می‌توان گفت که برای تولید سیگنال DSBSC  دو نوع مدولاتور وجود دارد. انواع مدولاتورهای DSBSC عبارتند از:

1. مدولاتور متعادل شده (Balanced Modulator)
2. مدولاتور حلقوی (Ring Modulator)

مدولاتور DSBSC متعادل شده

در تصویر زیر بلوک دیاگرام یک مدولاتور DSBSC متعادل شده نشان داده شده است.

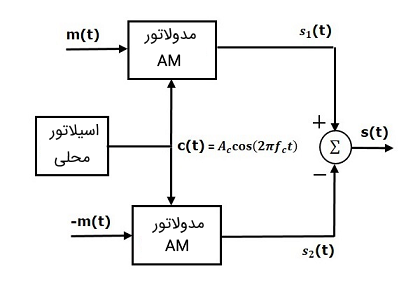
با دقت در بلوک دیاگرام فوق، می‌توان به این نتیجه رسید که یک مدولاتور DSBSC متعادل شده از دو مدولاتور AM مشابه با یکدیگر تشکیل شده است. این دو مدولاتور در یک پیکربندی متعادل قرار گرفته‌اند تا بتوانند سیگنال حامل را سرکوب (Suppress) کنند و به همین دلیل است که به این نوع مدولاتور، مدولاتور DSBSC متعادل شده می‌گویند.

فیلم آموزش مخابرات ۱ – مقدماتی

اینجا کلیک کنید

ابتدا توسط اسیلاتور محلی، یک سیگنال حامل با معادله زیر تولید می‌کنیم:

$$ c \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) $$

سپس این سیگنال حامل را به عنوان یکی از ورودی‌ها به دو مدار مدولاتور AM اعمال می‌کنیم. توجه کنید که سیگنال پیام $$ m \left ( t \right ) $$ به عنوان ورودی دیگر به مدولاتور AM بالایی (در تصویر فوق) وارد می‌شود. در حالی که همین سیگنال پیام $$ m \left ( t \right ) $$، اما این بار با پلاریته منفی، یا به عبارت دیگر $$ - m \left ( t \right ) $$ به ورودی دوم مدار مدولاتور AM پایین اعمال می‌شود. در این صورت، خروجی مدار مدولاتور AM بالایی را می‌توان به صورت رابطه ریاضی زیر بیان کرد:

$$ s _ 1 \left ( t \right ) = A _ c \left [ 1 + k _ a m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) $$

به طریق مشابه، رابطه ریاضی مدار مدولاتور AM پایینی را می‌توان به صورت زیر نوشت:

$$ s _ 2 \left ( t \right ) = A _ c \left [ 1 - k _ a m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) $$

حال با کمک روابط فوق و از طریق تفریق سیگنال $$ s _ 2 \left ( t \right ) $$ از سیگنال $$ s _ 1 \left ( t \right ) $$، می‌توان سیگنال $$ s \left ( t \right ) $$ مدولاسیون DSBSC را به دست آورد. بلوک جمع در نمایش بلوک دیاگرامی فوق، برای انجام همین عمل قرار داده شده است. سیگنال $$ s _ 1 \left ( t \right ) $$ با علامت مثبت و سیگنال $$ s _ 2 \left ( t \right ) $$ با علامت منفی به بلوک جمع کننده وارد می‌شوند. به همین دلیل است که این بلوک سیگنال $$ s \left ( t \right ) $$ را تولید می‌کند که حاصل تفریق $$ s _ 1 \left ( t \right ) $$ و $$ s _ 2 \left ( t \right ) $$ است.

حال سیگنال $$ s \left ( t \right ) $$ را می‌توان به کمک روابط ریاضی زیر بیان کرد:

$$ \Rightarrow s \left ( t \right ) = A _ c \left [ 1 + k _ a m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) - A _ c \left [ 1 - k _ a m \left ( t \right ) \right ] \cos \left ( 2 \pi f _ c t \right ) $$

$$ \Rightarrow s \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) + A _ c k _ a m \left ( t \right ) \cos \left ( 2 \pi f _ c t \right ) - \\ A _ c \cos \left ( 2 \pi f _ c t \right ) + A _ c k _ a m \left ( t \right ) \cos \left ( 2 \pi f _ c t \right ) $$

$$ \Rightarrow s \left ( t \right ) = 2 A _ c k _ a m \left ( t \right ) \cos \left ( 2 \pi f _ c t \right ) $$

از قبل می‌دانیم که معادله استاندارد یک سیگنال حامل سرکوب شده باند جانبی مضاعف یا DSBSC را می‌توان به صورت زیر نوشت:

$$ s \left ( t \right ) = A _ c m \left ( t \right ) \cos \left ( 2 \pi f _ c t \right ) $$

حال با مقایسه کردن مقدار سیگنال خروجی از بلوک جمع‌کننده مدار دمدولاتور متعادل شده DSBSC با معادله استاندار یک سیگنال مدولاسیون DSBSC، به این نتیجه می‌رسیم که سیگنال توسط یک فاکتور به اندازه $$ 2 k _ a $$ مقیاس (Scal) شده است.

فیلم آموزش مخابرات ۱ – مقدماتی

اینجا کلیک کنید

مدولاتور DSBSC حلقوی

در تصویر زیر مدار یک مدولاتور DSBSC حلقوی نشان داده شده است.

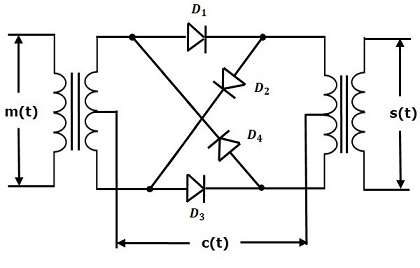
با دقت در مدار DSBSC حلقوی شکل فوق، متوجه می‌شویم که چهار دیود $$ D _ 1 $$ و $$ D _ 2 $$ و $$ D _ 3 $$ و $$ D _ 4 $$ با آرایش حلقوی به یکدیگر متصل شده‌اند. به همین دلیل است که این نوع از مدولاتور DSBSC را یک مدولاتور حلقوی می‌گویند. همچنین در این مدار یک ترانسفورمر با تپ دو سر (Two Center Tapped Transformers) مورد استفاده قرار می‌گیرد. سیگنال پیام $$ m \left ( t \right ) $$ به ورودی ترانسفورمر وارد می‌شود. همچنین در این مدار سیگنال حامل $$ c \left ( t \right ) $$ به وسط ترانسفورمر با تپ دو سر اعمال می‌شود.

برای نیم سیکل مثبت از سیگنال حامل، دیودهای $$ D _ 1 $$ و $$ D _ 3 $$ در مود بایاس مستقیم قرار می‌گیرند و روشن می‌شوند. در این حالت، دو دیود $$ D _ 2 $$ و $$ D _ 4 $$ در وضعیت خاموش هستند. در این شرایط، سیگنال پیام در عدد 1+ ضرب می‌شود.

برای نیم سیکل منفی از سیگنال حامل، دو دیود $$ D _ 2 $$ و $$ D _ 4 $$ در مود بایاس مستقیم قرار می‌گیرند و به وضعیت روشن تغییر حالت می‌یابند. این بار دیودهای $$ D _ 1 $$ و $$ D _ 3 $$ خاموش هستند. در این حالت، سیگنال پیام در عدد 1- ضرب می‌شود که این امر منجر به ۱۸۰ درجه شیفت فاز در سیگنال DSBSC حاصل می‌شود.

با استفاده از آنالیزی که در قسمت بالا انجام دادیم، می‌توانیم بگوییم که دیودهای $$ D _ 1 $$ و $$ D _ 2 $$ و $$ D _ 3 $$ و $$ D _ 4 $$ توسط سیگنال حامل کنترل می‌شوند. اگر سیگنال حامل دارای شکل موج مربعی باشد، آن‌گاه نمایش سری فوریه سیگنال حامل $$ c \left ( t \right ) $$ به صورت زیر خواهد بود:

$$ c \left ( t \right ) = \frac { 4 } { \pi} \sum _ { n = 1 } ^ { \infty } \frac { \left ( - 1 \right ) ^ { n - 1 } } { 2 n - 1 } \cos \left [2 \pi f _ c t \left ( 2 n - 1 \right ) \right ] $$

برای به دست آوردن سیگنال مدولاسیون DSBSC یا $$ s \left ( t \right ) $$، باید سیگنال حامل $$ c \left ( t \right ) $$ را در سیگنال پیام $$ m \left ( t \right ) $$ ضرب کنیم. در این صورت عبارت زیر برای سیگنال مدولاسیون DSBSC یا $$ s \left ( t \right ) $$ به دست می‌آید:

$$ s \left ( t \right ) = \frac { 4 } { \pi } \sum _ { n = 1 } ^ { \infty } \frac { \left ( - 1 \right ) ^ { n - 1 } } { 2 n - 1 } \cos \left [ 2 \pi f _ c t \left ( 2 n - 1 \right ) \right ] m \left ( t \right ) $$

معادله‌ای که در بالا به دست آمد، نشان دهنده یک سیگنال مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا DSBSC است. در مدار مدولاتور حلقوی DSBSC، این سیگنال را باید از خروجی ترانسفورماتور به دست آورد. توجه کنید که یک مدولاتور DSBSC را مدولاتور ضرب کننده (Product Modulator) نیز می‌گویند؛ زیرا این مدار مدولاتور قادر است خروجی را تولید کند که برابر با حاصل ضرب دو سیگنال ورودی است.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌های مهندسی برق
• آموزش الکترونیک ۱
• اسیلاتور کنترل شده با ولتاژ (VCO) — از صفر تا صد
• اشمیت تریگر با اپ امپ — از صفر تا صد
• نسبت سیگنال به نویز چیست؟ — از صفر تا صد

^^