فرادرسمجموع گاوس در ریاضیات | به زبان ساده
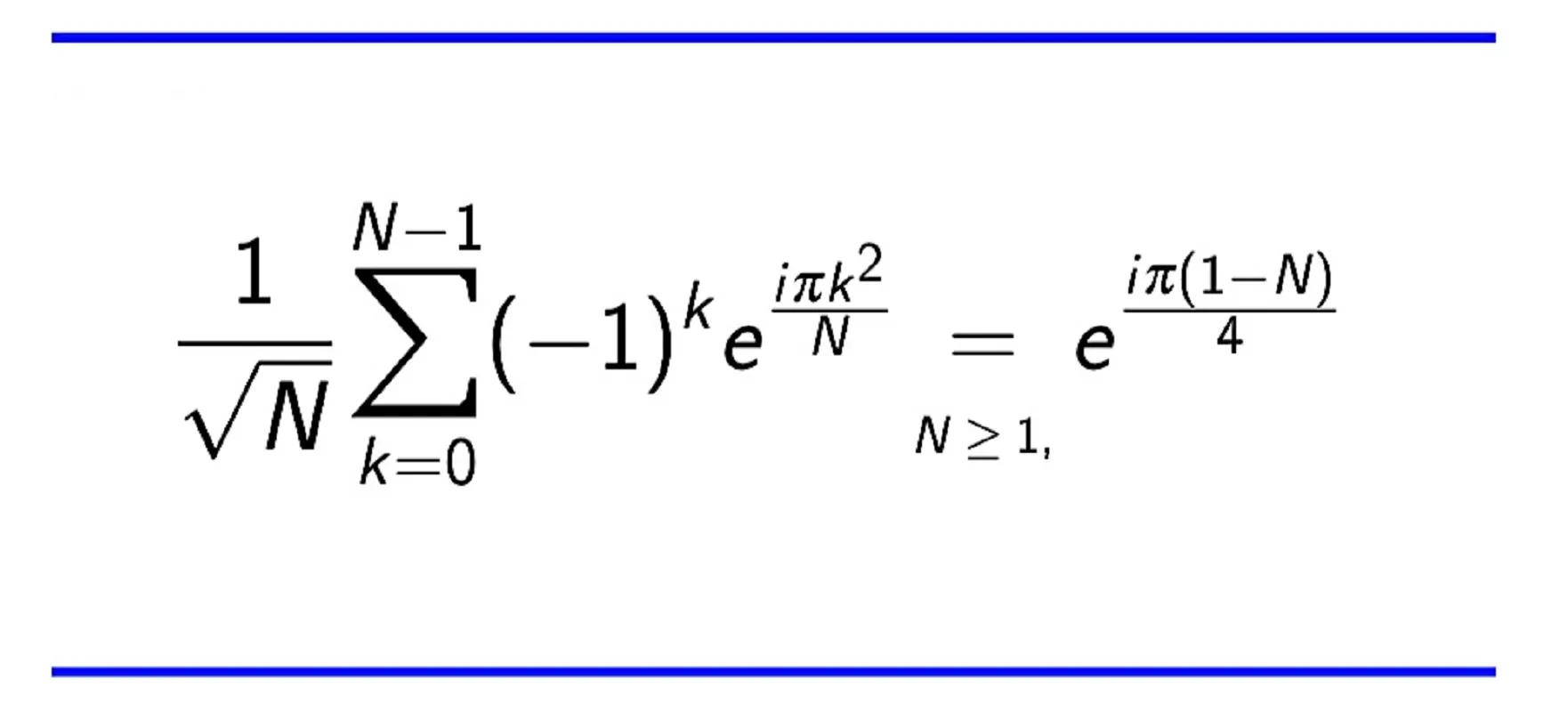
در «نظریه اعداد» (Number Theory)، جمع یا «مجموع گاوس» (Gauss Sum) یا «مجموع گاوسی» (Guassian Sum)، یک نوع جمع متناهی است که به ریشه واحد (Unit Root) بر می‌گردد. در این نوشتار به بررسی جمع گاوس در ریاضیات پرداخته و با مبانی آن آشنا می‌شویم.
برای آشنایی بیشتر با نظریه اعداد بهتر است ابتدا نوشتار نظریه اعداد و کاربردهای آن — به زبان ساده و میدان، حلقه و گروه در ریاضی – مفاهیم اولیه را مطالعه کنید. همچنین خواندن مطالب الگوها و دنباله های متداول عددی – به زبان ساده و قواعد بخش پذیری یا عاد کردن — به زبان ساده نیز خالی از لطف نیست.
مجموع گاوس در ریاضیات
«در نظریه جبری اعداد» (Algebra Number Theory)، «جمع گاوس» (Guass Sum) یا «مجموع گاوسی» (Gaussian Sum) یک نوع جمع متناهی محسوب می‌شود. این جمع را به صورت زیر نشان می‌دهند.
$$ \large G(\chi ): = G(\chi ,\psi ) = \sum \chi (r) \cdot \psi (r) $$
این جمع روی عناصر $$r$$ ساخته شده است که از یک حلقه جابجایی متناهی (finite commutative ring) مثل $$R$$ گرفته شده و $$\psi$$ یک گروه هم‌ریخت (homomorphism) از نوع گروه جمعی (additive group) مثل $$R^+$$ بر مبنای دایره‌ای به شعاع واحد است. همچنین $$\chi$$ نیز یک گروه هم‌ریخت از گروه واحد $$R^{\times}$$ به (Into) دایره واحد است. در نتیجه همانطور که دیده می‌شود این مجموع مرتبط با روی «ریشه‌های واحد» (Unit Root) خواهد بود. چنین جمعی، حالت توسعه یافته ریشه غیر واحد (non-unit) یا $$r$$ روی «میدان‌های متناهی» (Finite Fields) از تابع گاما هم در نظر گرفته شده است.
مجموع گاوسی در نظریه اعداد بسیار مورد استفاده قرار می‌گیرد. برای مثال از این جمع برای معادلات تابعک برای تابع دریکله استفاده می‌کنند. در این حالت معادله، یک رابطه‌ای بین $$L(s,\chi)$$ و $$L(1-s , \bar{\chi})$$ ایجاد می‌کند. مشخص است که $$\chi$$ کاراکتر دریکله و $$\bar{\chi}$$ هم مزدوج مختلط آن است. در این صورت عامل یا نسبت را به صورت زیر خواهیم داشت.
$$ \large {\displaystyle {\frac {G(\chi )}{ |G ( \chi )| }}} $$
تاریخچه مجموع گاوس
نظریه عمومی جمع‌های گاوس اولین بار در سال‌های ابتدایی قرن ۱۹ مورد بررسی قرار گرفت. «کارل گاوس» (Carl Freidrich Gauss) در مجموع مربعات روی اعداد حقیقی، چنین جمعی را مطرح کرد. او نشان داد که اگر $$p$$ یک عدد اول باشد، رابطه $$G(\chi)$$ برای نماد لاگرانژ ($$\chi$$)، برابر با $$p^{\frac{1}{2}}$$ یا $$ip^{\frac{1}{2}}$$ خواهد بود. البته به شرطی که $$p$$ متناسب با ۱ یا ۳ به پیمانه ۴ باشد.
مجموع مربعات گاوس را می‌توان به کمک «تحلیل فوریه» (Fourier Analysis) و «انتگرال کانتور» (Contour Integration) نیز بدست آورد. یک شیوه دیگر برای بیان جمع گاوس به صورت زیر است. این شیوه بسیار مرتبط با «توابع تتا» (Theta Functions) و نظریه مربوط به این گونه توابع است.
$$ \large \sum e^{ { { \dfrac { 2 \pi i r^{2} }{p}}} } $$
خصوصیات مجموع گاوس برای علائم دریکله
مجموع گاوس برای کاراکتر دریکله به پیمانه $$N$$، به صورت زیر نوشته می‌شود.
$$ \large {\displaystyle G(\chi ) = \sum_{a = 1}^{N} \chi (a) e^{ \frac {2\pi i a}{ N }}} $$
اگر $$\chi$$ یک مقدار اولیه (مثلا عدد اول) باشد، قدر مطلق رابطه بالا، به صورت زیر در خواهد آمد. واضح است که این مقدار غیر صفر است.
$$ \large |G(\chi )| = {\sqrt {N}}$$
در حالت کلی اگر $$N_0$$ یک کانداکتور (Conductor) برای $$\chi$$ (همان کاراکتر دریکله) باشد و $$\chi_0$$ نیز کاراکتر اولیه دریلکه به پیمانه $$N_0$$ باشد، آنگاه جمع گاوس روی $$\chi$$ که توسط $$\chi_0$$ تولید شده است به شکل زیر نمایش داده می‌شوند.
$$ \large {\displaystyle G( \chi ) = \mu \left( {\frac {N}{N_{0}}} \right) \chi _{0} \left( {\frac {N}{N_{0}}} \right) G \left( \chi _{0} \right) }$$
توجه داشته باشید که در اینجا منظور از $$\mu$$ همان «تابع موبیوس» (Möbius function) است. به این ترتیب $$G(\chi)$$ یک مقدار غیر صفر است به شرطی که نسبت $$\dfrac{N}{N_0}$$ نامربع و نسبت به $$N_0$$، اول باشد.
رابطه‌های دیگر بین $$G(\chi)$$ و جمع‌های گاوسی روی کاراکترهای دیگر به صورت زیر خلاصه می‌شوند.
$$ \large G(\overline { \chi }) = \chi (-1) \overline {G( \chi )}$$
در رابطه بالا منظور از $$\overline{\chi}$$، مزدوج مختلط کاراکتر دریکله است. همچنین اگر $$\chi'$$ یک کاراکتر دریکله به پیمانه $$N'$$ باشد بطوری که $$N$$ و $$N'$$ نسبت به هم اول در نظر گرفته شوند، آنگاه خواهیم داشت:
$$ \large {\displaystyle G \left( \chi \chi ^{\prime } \right) = \chi \left( N^{\prime } \right) \chi ^{\prime }(N)G(\chi )G\left(\chi ^{\prime } \right) } $$
رابطه بین $$G(\chi\chi')$$، $$G(\chi)$$ و $$G(\chi')$$ در زمانی که $$chi$$ و $$\chi'$$ بر یک پیمانه باشند و همچنین $$\chi \chi'$$ اول باشد، بوسیله «جمع ژاکوبی» (($$J(\chi, \chi'$$) اندازه گرفته می‌شود. در این صورت رابطه زیر برقرار خواهد بود.
$$ \large {\displaystyle G \left( \chi \chi ^{\prime } \right) = {\frac {G(\chi )G \left( \chi ^{\prime } \right) }{J\left( \chi ,\chi ^{\prime } \right) }}} $$
خواص زیر برای برای مجموع گاوسی نیز برقرار است.
- جمع گاوس را می‌توان برای اثبات تقابل درجه دوم، تقابل مکعب و تقابل درجه چهار استفاده کرد.
- از مجموع گاوس می‌توان برای محاسبه تعداد راه حل‌های معادلات چند جمله‌ای در میدان‌های متناهی استفاده کرد و بنابراین برای محاسبه برخی از «توابع زتا» (Zeta Function) نیز قابل استفاده است.
خلاصه و جمع بندی
از مجموع یا جمع گاوسی برای اثبات قانون و قضیه‌های تقابل مربعی و تقابل مکعبی نیز استفاده می‌شود. این قوانین نحوه جمع پذیری توان‌های دوم و سوم اعداد را مشخص می‌کنند. همچنین برای تعیین تعداد پاسخ‌ها یا ریشه‌های یک چند جمله‌ای از مجموع یا جمع گاوسی می‌توان استفاده کرد. در ریاضیات برای محاسبه مقادیر خاصی از «تابع زتا» (Zeta Function) نیز از جمع گاوسی بهره می‌برند.
